1.6E : Exercices

Last updated
Save as PDF

Page ID: 194248

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La pratique rend parfait

Utiliser les propriétés commutatives et associatives

Dans les exercices suivants, simplifiez.

1. $43m+(−12n)+(−16m)+(−9n)$

Réponse: $27m+(−21n)$

2. $−22p+17q+(−35p)+(−27q)$

3. $\frac{3}{8}g+\frac{1}{12}h+\frac{7}{8}g+\frac{5}{12}h$

Réponse: $\frac{5}{4}g+\frac{1}{2}h$

4. $\frac{5}{6}a+\frac{3}{10}b+\frac{1}{6}a+\frac{9}{10}b$

5. $6.8p+9.14q+(−4.37p)+(−0.88q)$

Réponse: $2.43p+8.26q$

6. $9.6m+7.22n+(−2.19m)+(−0.65n)$

7. $−24·7·\frac{3}{8}$

Réponse: $−63$

8. $−36·11·\frac{4}{9}$

9. $\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}$

Réponse: $1\frac{5}{6}$

10. $\left(\frac{11}{12}+\frac{4}{9}\right)+\frac{5}{9}$

11. $17(0.25)(4)$

Réponse: $17$

12. $36(0.2)(5)$

13. $[2.48(12)](0.5)$

Réponse: $14.88$

14. $[9.731(4)](0.75)$

15. $12\left(\frac{5}{6}p\right)$

Réponse: $10p$

16. $20\left(\frac{3}{5}q\right)$

Utiliser les propriétés Identity, Inverse et Zero

Dans les exercices suivants, simplifiez.

17. $19a+44−19a$

Réponse: $44$

18. $27c+16−27c$

19. $\frac{1}{2}+\frac{7}{8}+\left(−\frac{1}{2}\right)$

Réponse: $\frac{7}{8}$

20. $\frac{2}{5}+\frac{5}{12}+\left(−\frac{2}{5}\right)$

21. $10(0.1d)$

Réponse: $d$

22. $100(0.01p)$

23. $\frac{3}{20}·\frac{49}{11}·\frac{20}{3}$

Réponse: $\frac{49}{11}$

24. $\frac{13}{18}·\frac{25}{7}·\frac{18}{13}$

25. $\frac{0}{u−4.99}$, où$u\neq 4.99$

Réponse: $0$

26. $0÷(y−\frac{1}{6})$, où$x \neq 16$

27. $\frac{32−5a}{0}$, où$32−5a\neq 0$

Réponse: indéfini

28. $\frac{28−9b}{0}$, où$28−9b\neq 0$

29. $\left(\frac{3}{4}+\frac{9}{10}m\right)÷0$, où$\frac{3}{4}+\frac{9}{10}m\neq 0$

Réponse: indéfini

30. $\left(\frac{5}{16}n−\frac{3}{7}\right)÷0$, où$\frac{5}{16}n−\frac{3}{7}\neq 0$

Simplifier les expressions en utilisant la propriété distributive

Dans les exercices suivants, simplifiez l'utilisation de la propriété distributive.

31. $8(4y+9)$

Réponse: $32y+72$

32. $9(3w+7)$

33. $6(c−13)$

Réponse: $6c−78$

34. $7(y−13)$

35. $\frac{1}{4}(3q+12)$

Réponse: $\frac{3}{4}q+3$

36. $\frac{1}{5}(4m+20)$

37. $9(\frac{5}{9}y−\frac{1}{3})$

Réponse: $5y−3$

38. $10(\frac{3}{10}x−\frac{2}{5})$

39. $12(\frac{1}{4}+\frac{2}{3}r)$

Réponse: $3+8r$

40. $12(\frac{1}{6}+\frac{3}{4}s)$

41. $15⋅\frac{3}{5}(4d+10)$

Réponse: $36d+90$

42. $18⋅\frac{5}{6}(15h+24)$

43. $r(s−18)$

Réponse: $rs−18r$

44. $u(v−10)$

45. $(y+4)p$

Réponse: $yp+4p$

46. $(a+7)x$

47. $−7(4p+1)$

Réponse: $−28p−7$

48. $−9(9a+4)$

49. $−3(x−6)$

Réponse: $−3x+18$

50. $−4(q−7)$

51. $−(3x−7)$

Réponse: $−3x+7$

52. $−(5p−4)$

53. $16−3(y+8)$

Réponse: $−3y−8$

54. $18−4(x+2)$

55. $4−11(3c−2)$

Réponse: $−33c+26$

56. $9−6(7n−5)$

57. $22−(a+3)$

Réponse: $−a+19$

58. $8−(r−7)$

59. $(5m−3)−(m+7)$

Réponse: $4m−10$

60. $(4y−1)−(y−2)$

61. $9(8x−3)−(−2)$

Réponse: $72x−25$

62. $4(6x−1)−(−8)$

63. $5(2n+9)+12(n−3)$

Réponse: $22n+9$

64. $9(5u+8)+2(u−6)$

65. $14(c−1)−8(c−6)$

Réponse: $6c+34$

66. $11(n−7)−5(n−1)$

67. $6(7y+8)−(30y−15)$

Réponse: $12y+63$

68. $7(3n+9)−(4n−13)$

Exercices d'écriture

69. Dans vos propres termes, énoncez la propriété associative de l'addition.

Réponse: Les réponses peuvent varier.

70. Quelle est la différence entre l'inverse additif et l'inverse multiplicatif d'un nombre ?

71. Simplifiez l'$8(x−\frac{1}{4})$utilisation de la propriété distributive et expliquez chaque étape.

Réponse: Les réponses peuvent varier.

72. Expliquez comment vous pouvez multiplier$4($5.97)$ sans papier ni calculatrice en pensant à$$5.97$ la propriété distributive,$6−0.03$ puis en l'utilisant.

Auto-vérification

a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

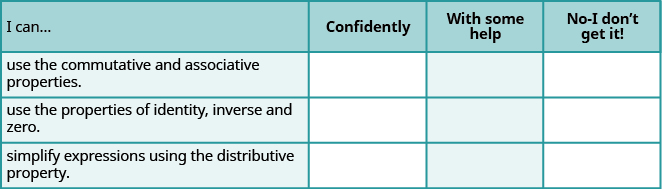
$Ce tableau comporte 4 colonnes, 3 lignes et une ligne d'en-tête. La ligne d'en-tête étiquette chaque colonne que je peux, en toute confiance, avec de l'aide et non, je ne comprends pas. La première colonne contient les instructions suivantes : utilisez les propriétés commutatives et associatives, utilisez les propriétés d'identité, inverse et zéro, simplifiez les expressions à l'aide de la propriété distributive. Les colonnes restantes sont vides.$

b. Après avoir examiné cette liste de contrôle, que ferez-vous pour atteindre tous les objectifs en toute confiance ?