Chapitre 1 Exercices de révision

Exercices de révision des

Utiliser le langage de l'algèbre

Identifier les multiples et les facteurs

1. Utilisez les tests de divisibilité pour déterminer si 180 est divisible par 2, par 3, par 5, par 6 et par 10.

Réponse

Divisible par$2,3,5,6$

2. Trouvez la factorisation première de 252.

3. Déterminez le multiple le moins courant de 24 et 40.

Réponse

120

Dans les exercices suivants, simplifiez chaque expression.

4. $24÷3+4(5−2)$

5. $7+3[6−4(5−4)]−3^2$

Réponse

4

Évaluer une expression

Dans les exercices suivants, évaluez les expressions suivantes.

6. Quand$x=4$, ⓐ $x^3$ ⓑ $5x$ ⓒ $2x^2−5x+3$

7. $2x^2−4xy−3y^2$quand$x=3$ et$y=1$

Réponse

3

Simplifiez les expressions en combinant des termes similaires

Dans les exercices suivants, simplifiez les expressions suivantes en combinant des termes similaires.

8. $12y+7+2y−5$

9. $14x^2−9x+11−8x^2+8x−6$

Réponse

$6x^2−x+5$

Traduire une phrase anglaise en une expression algébrique

Dans les exercices suivants, traduisez les phrases en expressions algébriques.

10. ⓐ la somme de$4ab^2$$7a3b24ab^2$ et$7a^3b^2$

ⓑ le produit de$6y^2$ et$3y$

ⓒ douze de plus que$5x$

ⓓ$5y$ inférieur à$8y^2$

11. ⓐ Onze fois la différence de$y$ et deux

ⓑ la différence de onze fois$y$ et deux

Réponse

ⓐ$11(y−2)$
ⓑ$11y−2$

12. Douchko a de l'argent et de l'argent en poche. Le nombre de pièces d'un cent est inférieur à cinq cents. Soit nn le nombre de nickels. Écrivez une expression pour le nombre de centimes.

Entiers

Simplifier les expressions avec une valeur

Dans l'exercice suivant, saisissez$<,>,$ ou$=$ pour chacune des paires de nombres suivantes.

13. ⓐ$−|7| \_\_\_−|−7|$

ⓑ$−8 \_\_\_−|−8|$

ⓒ$|−13| \_\_\_−13$

ⓓ$|−12| \_\_\_−(−12)$

Réponse

ⓐ$=$
ⓑ$=$
ⓒ$>$
ⓓ$=$

Dans les exercices suivants, simplifiez.

14. $9−|3(4−8)|$

15. $12−3|1−4(4−2)|$

Réponse

$−9$

Ajouter et soustraire des entiers

Dans les exercices suivants, simplifiez chaque expression.

16. $−12+(−8)+7$

17. ⓐ$15−7$

ⓑ$−15−(−7)$

ⓒ$−15−7$

ⓓ$15−(−7)$

Réponse

ⓐ$8$
ⓑ$−8$
ⓒ$−22$
ⓓ$22$

18. $−11−(−12)+5$

19. ⓐ$23−(−17)$ ⓑ$23+17$

Réponse

ⓐ 40 ⓑ 40

20. $−(7−11)−(3−5)$

Multipliez et divisez des entiers

Dans l'exercice suivant, multipliez ou divisez.

21. ⓐ$−27÷9$ ⓑ$120÷(−8)$ ⓒ$4(−14)$ ⓓ$−1(−17)$

Réponse

ⓐ$−3$ ⓑ$−15$ ⓒ$−56$ ⓓ$17$

Simplifier et évaluer des expressions avec des nombres entiers

Dans les exercices suivants, simplifiez chaque expression.

22. ⓐ$(−7)^3$ ⓑ$−7^3$

23. $(7−11)(6−13)$

Réponse

16

24. $63÷(−9)+(−36)÷(−4)$

25. $6−3|4(1−2)−(7−5)|$

Réponse

$−12$

26. $(−2)^4−24÷(13−5)$

Pour les exercices suivants, évaluez chaque expression.

27. $(y+z)^2$quand$y=−4$ et$z=7$

Réponse

9

28. $3x^2−2xy+4y^2$quand$x=−2$ et$y=−3$

Traduire des phrases anglaises en expressions algébriques

Dans les exercices suivants, traduisez en une expression algébrique et simplifiez si possible.

29. la somme de$−4$ et$−9$, augmentée de$23$

Réponse

$(−4+(−9))+23;10$

30. ⓐ la différence de 17 et −8 ⓑ soustraire 17 de −25

Utiliser des nombres entiers dans les applications

Dans l'exercice suivant, résolvez.

31. Température Le 10 juillet, la température maximale à Phoenix, en Arizona, était de 109° et la température maximale à Juneau, en Alaska, était de 63°. Quelle était la différence entre la température à Palm Springs et la température à Whitefield ?

Réponse

$46°$

Fractions

Simplifier les

Dans les exercices suivants, simplifiez.

32. $\dfrac{204}{228}$

33. $−\dfrac{270x^3}{198y^2}$

Réponse

$−\dfrac{15x^3}{11y^2}$

Multiplier et diviser des fractions

Dans les exercices suivants, effectuez l'opération indiquée.

34. $\left(−\dfrac{14}{15}\right)\left(\dfrac{10}{21}\right)$

35. $\dfrac{6x}{25}÷\dfrac{9y}{20}$

Réponse

$\dfrac{8x}{15y}$

36. $\dfrac{−\frac{4}{9}}{\dfrac{8}{21}}$

Ajouter et soustraire des fractions

Dans les exercices suivants, effectuez l'opération indiquée.

37. $\dfrac{5}{18}+\dfrac{7}{12}$

Réponse

$\dfrac{31}{36}$

38. $\dfrac{11}{36}−\dfrac{15}{48}$

39. ⓐ$\dfrac{5}{8}+\dfrac{3}{4}$ ⓑ$\dfrac{5}{8}÷\dfrac{3}{4}$

Réponse

ⓐ$\dfrac{11}{8}$ ⓑ$\dfrac{5}{6}$

40. ⓐ$−\dfrac{3y}{10}−\dfrac{5}{6}$ ⓑ$−\dfrac{3y}{10}·\dfrac{5}{6}$

Utiliser l'ordre des opérations pour simplifier les fractions

Dans les exercices suivants, simplifiez.

41. $\dfrac{4·3−2·5}{−6·3+2·3}$

Réponse

$−\dfrac{1}{6}$

42. $\dfrac{4(7−3)−2(4−9)}{−3(4+2)+7(3−6)}$

43. $\dfrac{4^3−4^2}{(\dfrac{4}{5})^2}$

Réponse

75

Évaluer des expressions variables avec des fractions

Dans les exercices suivants, évaluez.

44. $4x^2y^2$quand$x=\dfrac{2}{3}$ et$y=−\dfrac{3}{4}$

45. $\dfrac{a+b}{a−b}$quand$a=−4$ et$b=6$

Réponse

$−15$

Décimales

Décimales rondes

46. Arrondir$6.738$ au ⓐ centième ⓑ dixième ⓒ nombre entier le plus proche.

Ajouter et soustraire des décimales

Dans les exercices suivants, effectuez l'opération indiquée.

47. $−23.67+29.84$

Réponse

$6.17$

48. $54.3−100$

49. $79.38−(−17.598)$

Réponse

$96.978$

Multipliez et divisez les décimales

Dans les exercices suivants, effectuez l'opération indiquée.

50. $(−2.8)(3.97)$

51. $(−8.43)(−57.91)$

Réponse

488.1813

52. $(53.48)(10)$

53. $(0.563)(100)$

Réponse

$56.3$

54. $\$ 118.35÷2.6$

55. $1.84÷(−0.8)$

Réponse

$−23$

Convertir des nombres décimaux, des fractions et des pourcentages

Dans les exercices suivants, écrivez chaque décimale sous forme de fraction.

56. $\dfrac{13}{20}$

57. $−\dfrac{240}{25}$

Réponse

$−9.6$

Dans les exercices suivants, convertissez chaque fraction en décimale.

58. $−\dfrac{5}{8}$

59. $\dfrac{14}{11}$

Réponse

$1.\overline{27}$

Dans les exercices suivants, convertissez chaque décimale en pourcentage.

60. $2.43$

61. $0.0475$

Réponse

$4.75 \%$

Simplifiez les expressions avec des racines

Dans les exercices suivants, simplifiez.

62. $\sqrt{289}$

63. $\sqrt{−121}$

Réponse

aucun chiffre réel

Identifier les entiers, les nombres rationnels, les nombres irrationnels et les nombres réels

Dans l'exercice suivant, dressez la liste ⓐ des nombres entiers ⓑ des entiers ⓒ des nombres rationnels ⓓ des nombres irrationnels ⓔ des nombres réels pour chaque ensemble de nombres.

64. $−8,0,1.95286...,\dfrac{12}{5},\sqrt{36},9$

Localisez les fractions et les décimales sur la ligne numérique

Dans les exercices suivants, repérez les chiffres sur une ligne numérique.

65. $\dfrac{3}{4},−\dfrac{3}{4},1\dfrac{1}{3},−1\dfrac{2}{3},\dfrac{7}{2},−\dfrac{5}{2}$

Réponse

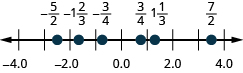
66. ⓐ$3.2$ ⓑ$−1.35$

Propriétés des nombres réels

Utiliser les propriétés commutatives et associatives

Dans les exercices suivants, simplifiez.

67. $\dfrac{5}{8}x+\dfrac{5}{12}y+\dfrac{1}{8}x+\dfrac{7}{12}y$

Réponse

$\dfrac{3}{4}x+y$

68. $−32·9·\dfrac{5}{8}$

69. $\left(\dfrac{11}{15}+\dfrac{3}{8}\right)+\dfrac{5}{8}$

Réponse

$1\dfrac{11}{15}$

Utiliser les propriétés Identity, Inverse et Zero

Dans les exercices suivants, simplifiez.

70. $\dfrac{4}{7}+\dfrac{8}{15}+\left(−\dfrac{4}{7}\right)$

71. $\dfrac{13}{15}·\dfrac{9}{17}·\dfrac{15}{13}$

Réponse

$\dfrac{9}{17}$

72. $\dfrac{0}{x−3},x\neq 3$

73. $\dfrac{5x−7}{0},5x−7\neq 0$

Réponse

indéfini

Simplifier les expressions en utilisant la propriété distributive

Dans les exercices suivants, simplifiez l'utilisation de la propriété distributive.

74. $8(a−4)$

75. $12\left(\dfrac{2}{3}b+\dfrac{5}{6}\right)$

Réponse

$8b+10$

76. $18·\dfrac{5}{6}(2x−5)$

77. $(x−5)p$

Réponse

$xp−5p$

78. $−4(y−3)$

79. $12−6(x+3)$

Réponse

$−6x−6$

80. $6(3x−4)−(−5)$

81. $5(2y+3)−(4y−1)$

Réponse

$y+16$

Test d'entraînement

1. Trouvez la factorisation principale de$756$.

2. Combinez des termes similaires :$5n+8+2n−1$

Réponse

$7n+7$

3. Évaluez quand$x=−2$ et$y=3: \dfrac{|3x−4y|}{6}$

4. Traduisez en une expression algébrique et simplifiez :

ⓐ onze de moins que moins huit

ⓑ la différence de$−8$ et$−3$, augmentée de 5

Réponse

$−8−11 = −19$
$(−8−(−3))+5 = 0$

5. Douchko a de l'argent et de l'argent en poche. Le nombre de pièces d'un cent est sept fois inférieur à quatre fois le nombre de pièces de cinq cents. Soit nn le nombre de nickels. Écrivez une expression pour le nombre de centimes.

6. Arrondir$28.1458$ au plus proche

ⓐ centième ⓑ millième

Réponse

ⓐ$28.15$ ⓑ$28.146$

7. Convertir

ⓐ$\dfrac{5}{11}$ à une décimale ⓑ$1.15$ à un pourcentage

8. Localisez$\dfrac{3}{5},2.8,and−\dfrac{5}{2}$ sur une ligne numérique.

Réponse

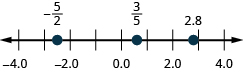
Dans les exercices suivants, simplifiez chaque expression.

9. $8+3[6−3(5−2)]−4^2$

10. $−(4−9)−(9−5)$

Réponse

1

11. $56÷(−8)+(−27)÷(−3)$

12. $16−2|3(1−4)−(8−5)|$

Réponse

$−8$

13. $−5+2(−3)^2−9$

14. $\dfrac{180}{204}$

Réponse

$\dfrac{15}{17}$

15. $−\dfrac{7}{18}+\dfrac{5}{12}$

16. $\dfrac{4}{5}÷(−\dfrac{12}{25})$

Réponse

$−\dfrac{5}{3}$

17. $\dfrac{9−3·9}{15−9}$

18. $\dfrac{4(−3+2(3−6))}{3(11−3(2+3))}$

Réponse

$3$

19. $\dfrac{5}{13}⋅\dfrac{4}{7}⋅\dfrac{13}{5}$

20. $\dfrac{−\dfrac{5}{9}}{\dfrac{10}{21}}$

Réponse

$−\dfrac{7}{6}$

21. $−4.8+(−6.7)$

22. $34.6−100$

Réponse

$−65.4$

23. $−12.04⋅(4.2)$

24. $−8÷0.05$

Réponse

160

25. $−\sqrt{121}$

26. $(\dfrac{8}{13}+\dfrac{5}{7})+\dfrac{2}{7}$

Réponse

$1\dfrac{8}{13}$

27. $5x+(−8y)−6x+3y$

28. ⓐ$\dfrac{0}{9}$ ⓑ$\dfrac{11}{0}$

Réponse

ⓐ 0 ⓑ non défini

29. $−3(8x−5)$

30. $6(3y−1)−(5y−3)$

Réponse

$13y−3$