1.6 : Propriétés des nombres réels
- Page ID
- 194242
À la fin de cette section, vous serez en mesure de :
- Utiliser les propriétés commutatives et associatives
- Utilisez les propriétés d'identité, d'inverse et de zéro
- Simplifier les expressions en utilisant la propriété distributive
Utiliser les propriétés commutatives et associatives
L'ordre dans lequel nous ajoutons deux nombres n'affecte pas le résultat. Si nous ajoutons\(8+9\) ou\(9+8\), les résultats sont les mêmes : ils sont tous deux égaux à 17. Donc,\(8+9=9+8\). L'ordre dans lequel nous ajoutons n'a pas d'importance !
De même, lorsque vous multipliez deux nombres, l'ordre n'affecte pas le résultat. Si nous multiplions\(9·8\) ou si\(8·9\) les résultats sont identiques, ils sont tous deux égaux à 72. Donc,\(9·8=8·9\). L'ordre dans lequel nous multiplions n'a pas d'importance ! Ces exemples illustrent la propriété commutative.
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \]
Lorsque vous ajoutez ou multipliez, la modification de l'ordre donne le même résultat.
La propriété commutative est liée à l'ordre. On soustrait\(9−8\) et\(8−9\) on voit ça\(9−8\neq 8−9\). Comme le changement de l'ordre de la soustraction ne donne pas le même résultat, nous savons que la soustraction n'est pas commutative.
La division n'est pas non plus commutative. Depuis\(12÷3\neq 3÷12\), la modification de l'ordre de la division n'a pas donné le même résultat. Les propriétés commutatives s'appliquent uniquement à l'addition et à la multiplication !
- L'addition et la multiplication sont commutatives.
- La soustraction et la division ne sont pas commutatives.
Lorsque vous ajoutez trois nombres, la modification du regroupement des nombres donne le même résultat. Par exemple\((7+8)+2=7+(8+2)\), puisque chaque côté de l'équation est égal à 17.
Cela vaut également pour la multiplication. Par exemple\(\left(5·\frac{1}{3}\right)·3=5·\left(\frac{1}{3}·3\right)\), puisque chaque côté de l'équation est égal à 5.
Ces exemples illustrent la propriété associative.
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \]
Lors de l'ajout ou de la multiplication, la modification du regroupement donne le même résultat.
La propriété associative concerne le regroupement. Si nous changeons la façon dont les nombres sont regroupés, le résultat sera le même. Remarquez qu'il s'agit des trois mêmes nombres dans le même ordre, la seule différence étant le regroupement.
Nous avons vu que la soustraction et la division n'étaient pas commutatives. Ils ne sont pas associatifs non plus.
\[\begin{array}{cc} (10−3)−2\neq 10−(3−2) & (24÷4)÷2\neq 24÷(4÷2) \\ 7−2\neq 10−1 & 6÷2\neq 24÷2 \\ 5\neq 9 & 3\neq 12 \end{array}\]
Lorsque vous simplifiez une expression, il est toujours judicieux de planifier les étapes à suivre. Afin de combiner des termes similaires dans l'exemple suivant, nous utiliserons la propriété commutative d'addition pour écrire les termes similaires ensemble.
Simplifiez :\(18p+6q+15p+5q\).
- Réponse
-
\[\begin{array}{lc} \text{} & 18p+6q+15p+5q \\ \text{Use the Commutative Property of addition to} & 18p+15p+6q+5q \\ \text{reorder so that like terms are together.} & {} \\ \text{Add like terms.} & 33p+11q \end{array}\]
Simplifiez :\(23r+14s+9r+15s\).
- Réponse
-
\(32r+29s\)
Simplifiez :\(37m+21n+4m−15n\).
- Réponse
-
\(41m+6n\)
Lorsque nous devons simplifier des expressions algébriques, nous pouvons souvent faciliter le travail en appliquant d'abord la propriété commutative ou la propriété associative.
Simplifiez :\((\frac{5}{13}+\frac{3}{4})+\frac{1}{4}\).
- Réponse
-
\( \begin{array}{lc} \text{} & (\frac{5}{13}+\frac{3}{4})+\frac{1}{4} \\ {\text{Notice that the last 2 terms have a common} \\ \text{denominator, so change the grouping.} } & \frac{5}{13}+(\frac{3}{4}+\frac{1}{4}) \\ \text{Add in parentheses first.} & \frac{5}{13}+(\frac{4}{4}) \\ \text{Simplify the fraction.} & \frac{5}{13}+1 \\ \text{Add.} & 1\frac{5}{13} \\ \text{Convert to an improper fraction.} & \frac{18}{13} \end{array}\)
Simplifiez :\((\frac{7}{15}+\frac{5}{8})+\frac{3}{8}.\)
- Réponse
-
\(1 \frac{7}{15}\)
Simplifiez :\((\frac{2}{9}+\frac{7}{12})+\frac{5}{12}\).
- Réponse
-
\(1\frac{2}{9}\)
Utiliser les propriétés Identity, Inverse et Zero
Que se passe-t-il lorsque nous ajoutons 0 à un nombre ? L'ajout de 0 ne modifie pas la valeur. Pour cette raison, nous appelons 0 l'identité additive. La propriété d'identité de l'addition qui indique que pour tout nombre réel\(a,a+0=a\) et\(0+a=a.\)
Que se passe-t-il lorsque nous multiplions un nombre par un ? La multiplication par 1 ne modifie pas la valeur. Nous appelons donc 1 l'identité multiplicative. La propriété d'identité de la multiplication qui indique que pour tout nombre réel\(a,a·1=a\) et\(1⋅a=a.\)
Nous résumons les propriétés d'identité ici.
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \\ \\ \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \\ \\ \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\]
Quel chiffre ajouté à 5 donne l'identité additive, 0 ? Nous savons
.jpg)
Le numéro manquant était le contraire du numéro !
Nous appelons\(−a\) l'inverse additif de\(a\). L'opposé d'un nombre est son inverse additif. Un nombre et son opposé s'additionnent à zéro, qui est l'identité additive. Cela conduit à la propriété inverse de l'addition qui indique pour n'importe quel nombre réel\(a,a+(−a)=0.\)
Quel nombre multiplié par\(\frac{2}{3}\) donne l'identité multiplicative, 1 ? En d'autres termes,\(\frac{2}{3}\) multiplié par quel résultat 1 ? Nous savons
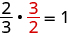
Le nombre manquant était l'inverse du nombre !
Nous appelons\(\frac{1}{a}\) l'inverse multiplicatif de a. L'inverse d'un nombre est son inverse multiplicatif. Cela conduit à la propriété inverse de la multiplication qui indique que pour tout nombre réel\(a,a\neq 0,a·\frac{1}{a}=1.\)
Nous allons énoncer formellement les propriétés inverses ici.
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\]
La propriété d'identité de l'addition indique que lorsque nous ajoutons 0 à un nombre, le résultat est le même nombre. Que se passe-t-il lorsque nous multiplions un nombre par 0 ? En multipliant par 0, le produit est égal à zéro.
Qu'en est-il de la division impliquant zéro ? Qu'\(0÷3\)est-ce que c'est Prenons un exemple concret : s'il n'y a pas de biscuits dans la boîte à biscuits et que 3 personnes doivent les partager, combien de biscuits reçoit chaque personne ? Il n'y a aucun cookie à partager, donc chaque personne reçoit 0 cookie. Donc,\(0÷3=0.\)
Nous pouvons vérifier la division avec le fait de multiplication correspondant. Nous le savons donc\(0÷3=0\) parce que\(0·3=0\).
Maintenant, pensez à diviser par zéro. Quel est le résultat de la division de 4 par 0 ? Pensez au fait de multiplication connexe :

Y a-t-il un nombre qui, multiplié par 0, donne 4 ? Comme tout nombre réel multiplié par 0 donne 0, aucun nombre réel ne peut être multiplié par 0 pour obtenir 4. Nous concluons qu'il n'y a pas de réponse\(4÷0\) et nous disons donc que la division par 0 n'est pas définie.
Nous résumons les propriétés de zéro ici.
Multiplication par zéro : Pour tout nombre réel a,
\[a⋅0=0 \; \; \; 0⋅a=0 \; \; \; \; \text{The product of any number and 0 is 0.}\]
Division par zéro : Pour tout nombre réel a,\(a\neq 0\)
\[\begin{array}{cl} \dfrac{0}{a}=0 & \text{Zero divided by any real number, except itself, is zero.} \\ \dfrac{a}{0} \text{ is undefined} & \text{Division by zero is undefined.} \end{array}\]
Nous allons maintenant nous entraîner à utiliser les propriétés des identités, des inverses et du zéro pour simplifier les expressions.
Simplifiez :\(−84n+(−73n)+84n.\)
- Réponse
-
\(\begin{array}{lc} \text{} & −84n+(−73n)+84n \\ \text{Notice that the first and third terms are} \\ \text{opposites; use the Commutative Property of} & −84n+84n+(−73n) \\ \text{addition to re-order the terms.} \\ \text{Add left to right.} & 0+(−73n) \\ \text{Add.} & −73n \end{array}\)
Simplifiez :\(−27a+(−48a)+27a\).
- Réponse
-
\(−48a\)
Simplifiez :\(39x+(−92x)+(−39x)\).
- Réponse
-
\(−92x\)
Nous allons maintenant voir à quel point il est utile de reconnaître les réciprocités. Avant de multiplier de gauche à droite, recherchez les réciproques : leur produit est 1.
Simplifiez :\(\frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7}\).
- Réponse
-
\(\begin{array}{lc} \text{} & \frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7} \\ \text{Notice the first and third terms} \\ {\text{are reciprocals, so use the Commutative} \\ \text{Property of multiplication to re-order the} \\ \text{factors.}} & \frac{7}{15}·\frac{15}{7}·\frac{8}{23} \\ \text{Multiply left to right.} & 1·\frac{8}{23} \\ \text{Multiply.} & \frac{8}{23} \end{array}\)
Simplifiez :\(\frac{9}{16}⋅\frac{5}{49}⋅\frac{16}{9}\).
- Réponse
-
\(\frac{5}{49}\)
Simplifiez :\(\frac{6}{17}⋅\frac{11}{25}⋅\frac{17}{6}\).
- Réponse
-
\(\frac{11}{25}\)
L'exemple suivant nous fait prendre conscience de la distinction entre diviser 0 par un nombre ou diviser un nombre par 0.
Simplifier : a.\(\frac{0}{n+5}\), où\(n\neq −5\) b.\(\frac{10−3p}{0}\) où\(10−3p\neq 0.\)
- Réponse
-
un.
\(\begin{array}{lc} {} & \dfrac{0}{n+5} \\ \text{Zero divided by any real number except itself is 0.} & 0 \end{array}\)
b.
\(\begin{array}{lc} {} & \dfrac{10−3p}{0} \\ \text{Division by 0 is undefined.} & \text{undefined} \end{array}\)
Simplifier : a.\(\frac{0}{m+7}\), où\(m\neq −7\) b.\(\frac{18−6c}{0}\), où\(18−6c\neq 0\).
- Réponse
-
a. 0
b. non défini
Simplifier : a.\(\frac{0}{d−4}\), où\(d\neq 4\) b.\(\frac{15−4q}{0}\), où\(15−4q\neq 0\).
- Réponse
-
a. 0
b. non défini
Simplifier les expressions en utilisant la propriété distributive
Supposons que trois amis vont au cinéma. Ils ont chacun besoin de 9,25$, soit 9 dollars et un quart, pour payer leurs billets. De combien d'argent ont-ils besoin en tout ?
Vous pouvez penser aux dollars séparément des trimestres. Ils ont besoin de 3 fois 9$ donc 27$ et 3 fois 1 trimestre, soit 75 cents. Au total, ils ont besoin de 27,75$. Si vous envisagez de faire le calcul de cette manière, vous utilisez la propriété distributive.
\(\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\)
En algèbre, nous utilisons la propriété distributive pour supprimer les parenthèses lors de la simplification des expressions.
Simplifiez :\(3(x+4)\).
- Réponse
-
\(\begin{array} {} & 3(x+4) \\ \text{Distribute.} \; \; \; \; \; \; \; \; & 3·x+3·4 \\ \text{Multiply.} & 3x+12 \end{array}\)
Simplifiez :\(4(x+2)\).
- Réponse
-
\(4x8\)
Simplifiez :\(6(x+7)\).
- Réponse
-
\(6x42\)
Certains élèves trouvent utile de dessiner des flèches pour leur rappeler comment utiliser la propriété distributive. La première étape de l'exemple devrait alors ressembler à ceci :
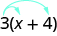
Simplifiez :\(8(\frac{3}{8}x+\frac{1}{4})\).
- Réponse
-
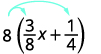
Distribuez. 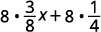
Multipliez. 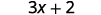
Simplifiez :\(6(\frac{5}{6}y+\frac{1}{2})\).
- Réponse
-
\(5y+3\)
Simplifiez :\(12(\frac{1}{3}n+\frac{3}{4})\)
- Réponse
-
\(4n+9\)
L'utilisation de la propriété distributive, comme indiqué dans l'exemple suivant, sera très utile lorsque nous résoudrons des demandes d'argent dans les chapitres suivants.
Simplifiez :\(100(0.3+0.25q)\).
- Réponse
-
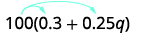
Distribuez. 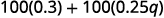
Multipliez. 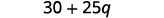
Simplifiez :\(100(0.7+0.15p).\)
- Réponse
-
\(70+15p\)
Simplifiez :\(100(0.04+0.35d)\).
- Réponse
-
\(4+35d\)
Lorsque nous distribuons un nombre négatif, nous devons faire très attention à ce que les signes soient corrects !
Simplifiez :\(−11(4−3a).\)
- Réponse
-
\(\begin{array}{lc} {} & −11(4−3a) \\ \text{Distribute. } \; \; \; \; \; \; \; \; \; \;& −11·4−(−11)·3a \\ \text{Multiply.} & −44−(−33a) \\ \text{Simplify.} & −44+33a \end{array}\)
Notez que vous pouvez également écrire le résultat sous la forme\(33a−44.\) Savez-vous pourquoi ?
Simplifiez :\(−5(2−3a)\).
- Réponse
-
\(−10+15a\)
Simplifiez :\(−7(8−15y).\)
- Réponse
-
\(−56+105y\)
Dans l'exemple suivant, nous allons montrer comment utiliser la propriété distributive pour trouver le contraire d'une expression.
Simplifiez :\(−(y+5)\).
- Réponse
-
\(\begin{array}{lc} {} & −(y+5) \\ \text{Multiplying by }−1 \text{ results in the opposite.}& −1(y+5) \\ \text{Distribute.} & −1·y+(−1)·5 \\ \text{Simplify.} & −y+(−5) \\ \text{Simplify.} & −y−5 \end{array} \)
Simplifiez :\(−(z−11)\).
- Réponse
-
\(−z+11\)
Simplifiez :\(−(x−4)\).
- Réponse
-
\(−x+4\)
Il y aura des moments où nous devrons utiliser la propriété distributive dans le cadre de l'ordre des opérations. Commencez par regarder les parenthèses. Si l'expression entre parenthèses ne peut pas être simplifiée, l'étape suivante consiste à effectuer une multiplication à l'aide de la propriété distributive, qui supprime les parenthèses. Les deux exemples suivants illustreront cela.
Simplifiez :\(8−2(x+3)\)
- Réponse
-
Nous suivons l'ordre des opérations. La multiplication vient avant la soustraction, nous allons donc d'abord distribuer les 2 puis les soustraire.
\(\begin{array}{lc} {} & \text{8−2(x+3)} \\ \text{Distribute.} & 8−2·x−2·3 \\ \text{Multiply.} & 8−2x−6 \\ \text{Combine like terms.} &−2x+2 \end{array}\)
Simplifiez :\(9−3(x+2)\).
- Réponse
-
\(3−3x\)
Simplifiez :\(7x−5(x+4)\).
- Réponse
-
\(2x−20\)
Simplifiez :\(4(x−8)−(x+3)\).
- Réponse
-
\(\begin{array}{lc} {} & 4(x−8)−(x+3) \\ \text{Distribute.} & 4x−32−x−3 \\ \text{Combine like terms.} & 3x−35 \end{array}\)
Simplifiez :\(6(x−9)−(x+12)\).
- Réponse
-
\(5x−66\)
Simplifiez :\(8(x−1)−(x+5)\).
- Réponse
-
\(7x−13\)
Toutes les propriétés des nombres réels que nous avons utilisées dans ce chapitre sont résumées ici.
| Propriété commutative
Lors de l'ajout ou de la multiplication, la modification de l'ordre donne le même résultat \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| Propriété associative
Lors de l'ajout ou de la multiplication, la modification du regroupement donne le même résultat. \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| Propriété distributive
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| Propriété d'identité \[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| Propriété inverse
\[\begin{array}{lc} \textbf{of addition } \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| Propriétés de Zero \[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
Concepts clés
| Propriété de commutation Lors de l'addition ou de la multiplication, la modification de l'ordre donne le même résultat \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| Propriété associative Lors de l'ajout ou de la multiplication, la modification du regroupement donne le même résultat. \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| Propriété distributive
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| Propriété d'identité
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| Propriété inverse
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| Propriétés de Zero
\[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
Lexique
- identité additive
- Le chiffre 0 est l'identité additive, car l'ajout de 0 à un nombre ne modifie pas sa valeur.
- inverse additif
- L'opposé d'un nombre est son inverse additif.
- identité multiplicative
- Le chiffre 1 est l'identité multiplicative car le fait de multiplier 1 par n'importe quel nombre ne modifie pas sa valeur.
- inverse multiplicatif
- L'inverse d'un nombre est son inverse multiplicatif.


