1.5 : Décimales
- Page ID
- 194261
À la fin de cette section, vous serez en mesure de :
- Décimales rondes
- Ajouter et soustraire des décimales
- Multipliez et divisez les décimales
- Convertir des décimales, des fractions et des pourcentages
- Simplifiez les expressions avec des racines
- Identifiez les entiers, les nombres rationnels, les nombres irrationnels et les nombres réels
- Localisez les fractions et les décimales sur la ligne numérique
Une introduction plus complète aux sujets abordés dans cette section se trouve dans le chapitre sur l'algèbre élémentaire, Fondations.
Décimales rondes
Les décimales sont une autre façon d'écrire des fractions dont les dénominateurs sont des puissances de dix.
\[\begin{array}{rcll} 0.1 & = & \dfrac{1}{10} & \text{is “one tenth”} \\ 0.01 & = & \dfrac{1}{100} & \text{is “one hundredth”} \\ 0.001 & = & \dfrac{1}{1000} & \text{is “one thousandth”} \\ 0.0001 & = & \dfrac{1}{10,000} & \text{is “one ten-thousandth”} \end{array}\]
Tout comme pour les nombres entiers, chaque chiffre d'une décimale correspond à la valeur de position basée sur la puissance de dix. La figure montre les noms des valeurs de position à gauche et à droite de la virgule décimale.
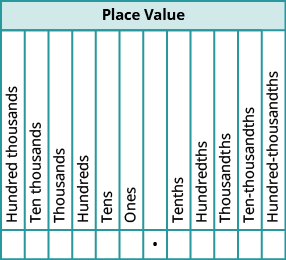
Lorsque nous travaillons avec des décimales, il est souvent nécessaire d'arrondir le nombre à la valeur décimale la plus proche. Nous résumons ici les étapes pour arrondir une décimale.
- Localisez la valeur de position donnée et marquez-la avec une flèche.
- Soulignez le chiffre situé à droite de la valeur de la position.
- Le chiffre souligné est-il supérieur ou égal à 5 ?
- Oui : ajoutez 1 au chiffre dans la valeur de position donnée.
- Non : ne modifiez pas le chiffre dans la valeur de position indiquée
- Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi.
Arrondir\(18.379\) au ⓐ centième ⓑ dixième ⓒ nombre entier le plus proche.
- Réponse
-
Ronde\(18.379.\)
ⓐ au centième le plus proche
Localisez la centième place à l'aide d'une flèche. 
Soulignez le chiffre situé à droite de la valeur de position donnée. 
Comme 9 est supérieur ou égal à 5, ajoutez 1 au 7. 
Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi. 
Notez que les chiffres supprimés n'ont PAS été remplacés par des zéros. 
ⓑ au dixième le plus proche
Localisez la dixième place à l'aide d'une flèche. 
Soulignez le chiffre situé à droite de la valeur de position donnée. 
Comme 7 est supérieur ou égal à 5, ajoutez 1 au 3. 
Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi. 
Notez que les chiffres supprimés n'ont PAS été remplacés par des zéros. 
ⓒ au nombre entier le plus proche
Localisez leur emplacement à l'aide d'une flèche. 
Soulignez le chiffre situé à droite de la valeur de position donnée. 
Puisque 3 n'est pas supérieur ou égal à 5, n'ajoutez pas 1 au 8. 
Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi. 

Arrondir\(6.582\) au ⓐ centième ⓑ dixième ⓒ nombre entier le plus proche.
- Réponse
-
ⓐ\(6.58\) ⓑ\(6.6\) ⓒ\(7\)
Arrondir\(15.2175\) au ⓐ millième ⓑ centième ⓒ dixième le plus proche.
- Réponse
-
ⓐ\(15.218\) ⓑ\(15.22\)
ⓒ\(15.2\)
Ajouter et soustraire des décimales
Pour ajouter ou soustraire des décimales, nous alignons les décimales. En alignant les décimales de cette façon, nous pouvons ajouter ou soustraire les valeurs de position correspondantes. Nous ajoutons ou soustrayons ensuite les nombres comme s'il s'agissait de nombres entiers, puis nous plaçons le point décimal dans la somme.
- Déterminez le signe de la somme ou de la différence.
- Écrivez les nombres de manière à ce que les décimales soient alignées verticalement.
- Utilisez des zéros comme espaces réservés, selon les besoins.
- Ajoutez ou soustrayez les nombres comme s'il s'agissait de nombres entiers. Placez ensuite le point
décimal dans la réponse sous les décimales des nombres donnés. - Écrivez la somme ou la différence avec le signe approprié.
Ajouter ou soustraire : ⓐ\(−23.5−41.38\) ⓑ\(14.65−20.\)
- Réponse
-
ⓐ
\(\begin{array}{ll} \text{} & −23.5−41.38 \\ \\ \\ {\text{The difference will be negative. To subtract, we add the} \\ \text{numerals. Write the numbers so the decimal points line} \\ \text{up vertically.}} & { \; \; 23.5 \\ \underline{+41.38}} \\ \\ \\ { \text{Put 0 as a placeholder after the 5 in 23.5.} \\ \text{Remember, } \frac{5}{10}=\frac{50}{100} \text{ so } 0.5=0.50.} & { \; \; 23.50 \\ \underline{+41.38}} \\ \\ \\ {\text{Add the numbers as if they were whole numbers.} \\ \text{Then place the decimal point in the sum.}} & {\; \; 23.50 \\ \underline{+41.38} \\ \; \; 64.88 } \\ \\ \\ \text{ Write the result with the correct sign.} & 64.88−23.5−41.38=−64.88 \end{array}\)
ⓑ
\(\begin{array}{ll} \text{} & 14.65−20 \\ \\ \\ {\text{The difference will be negative. To subtract, we} \\ \text{subtract 14.65 from 20.}} \\ \\ \\ {\text{Write the numbers so the decimal points line up} \\ \text{vertically.}} & { \; \; 20 \\ \underline{−14.65}} \\ \\ \\ {\text{Remember, 20 is a whole number, so place the} \\ \text{decimal point after the 0.}} \\ \\ \\ \text{Put in zeros to the right as placeholders.} & { \; \; 20.00 \\ \underline{−14.65}} \\ \\ \\ \text{Subtract and place the decimal point in the answer.} & {\begin{array}{lcccc} {} & 9 & {} & 9 & {} \\ 1 & \cancel{10} & {} & \cancel{10} & 10 \\ 2 & 0 & . & 0 & 0 \\ −1 & 4 & . & 6 & 5 \end{array} \\ \text{______________________} \\ \begin{array}{lcccc} {\; \; \; \; \; \; \; \; \; } & 5 & . & 3 & 5 \end{array}} \\ \\ \\ \text{Write the result with the correct sign.} & 14.65−20=−5.35 \end{array} \)
Ajoutez ou soustrayez : ⓐ\(−4.8−11.69\) ⓑ\(9.58−10\).
- Réponse
-
ⓐ\(−16.49\) ⓑ\(−0.42\)
Ajoutez ou soustrayez : ⓐ\(−5.123−18.47\) ⓑ\(37.42−50\).
- Réponse
-
ⓐ\(−23.593\) ⓑ\(−12.58\)
Multipliez et divisez les décimales
Lorsque nous multiplions des décimales signées, nous déterminons d'abord le signe du produit, puis nous multiplions comme si les nombres étaient tous deux positifs. Nous multiplions les nombres temporairement en ignorant la virgule décimale, puis nous comptons le nombre de décimales dans les facteurs et cette somme nous indique le nombre de décimales dans le produit. Enfin, nous écrivons le produit avec le signe approprié.
- Déterminez le signe du produit.
- Écrivez au format vertical en alignant les chiffres sur la droite. Multipliez les nombres comme s'ils étaient des nombres entiers, en ignorant temporairement les décimales.
- Placez le point décimal. Le nombre de décimales dans le produit est la somme
du nombre de décimales des facteurs. - Écrivez le produit avec le signe approprié.
Multipliez :\((−3.9)(4.075)\).
- Réponse
-
\((−3.9)(4.075)\) Les signes sont différents. Le produit
sera négatif.Le produit sera négatif. Écrivez au format vertical en alignant les
chiffres sur la droite.
Multipliez. 
Additionnez le nombre de décimales dans
les facteurs (1 + 3). Placez la virgule décimale à 4 places en partant de la droite.

Les signes sont différents, donc le produit est négatif. \((−3.9)(4.075)=−15.8925\)
Multipliez :\(−4.5(6.107)\).
- Réponse
-
\(−27.4815\)
Multipliez :\(−10.79(8.12)\).
- Réponse
-
\(−87.6148\)
Souvent, surtout dans les sciences, vous multiplierez les décimales par des puissances de 10 (10, 100, 1000, etc.). Si vous multipliez quelques produits sur du papier, vous remarquerez peut-être un schéma reliant le nombre de zéros de la puissance de 10 au nombre de décimales : nous déplaçons la virgule décimale vers la droite pour obtenir le produit.
- Déplacez la virgule décimale vers la droite autant de places que le
nombre de zéros de la puissance 10. - Ajoutez des zéros à la fin du numéro si nécessaire.
Multipliez : 5,63 par ⓐ 10 ⓑ 100 ⓒ 1000.
- Réponse
-
En regardant le nombre de zéros dans le multiple de dix, nous voyons le nombre de décimales dont nous avons besoin pour déplacer la décimale vers la droite.
ⓐ
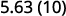
Il y a 1 zéro sur 10, donc déplacez la virgule décimale d'une place vers la droite. 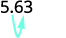
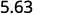
ⓑ
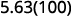
Il y a 2 zéros sur 100, déplacez donc la virgule décimale de 2 places vers la droite. 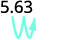

ⓒ
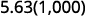
Il y a 3 zéros sur 1 000, donc déplacez la virgule décimale de 3 points vers la droite. 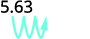
Un zéro doit être ajouté à la fin. 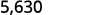
Multipliez 2,58 par ⓐ 10 ⓑ 100 ⓒ 1000.
- Réponse
-
ⓐ 25,8 ⓑ 258 ⓒ 2 580
Multipliez 14,2 par ⓐ 10 ⓑ 100 ⓒ 1000.
- Réponse
-
ⓐ 142 ⓑ 1 420 ⓒ 14 200
Tout comme pour la multiplication, la division de décimales signées ressemble beaucoup à la division de nombres entiers. Il suffit de déterminer où doit être placée la virgule décimale et le signe du quotient. Lorsque vous divisez des nombres décimaux signés, déterminez d'abord le signe du quotient, puis divisez comme si les deux nombres étaient positifs. Enfin, écrivez le quotient avec le signe approprié.
Nous passons en revue la notation et le vocabulaire de la division :

Nous allons écrire les étapes à suivre lors de la division des décimales pour faciliter la consultation.
- Déterminez le signe du quotient.
- Faites du diviseur un nombre entier en « déplaçant » la virgule complètement vers la droite. « Déplacez » la virgule décimale du dividende du même nombre de positions, en ajoutant des zéros si nécessaire.
- Diviser. Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende.
- Écrivez le quotient avec le signe approprié.
Diviser :\(−25.65÷(−0.06)\).
- Réponse
-
N'oubliez pas que vous pouvez « déplacer » les décimales du diviseur et du dividende grâce à la propriété Fractions équivalentes.
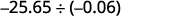
Les signes sont les mêmes. Le quotient est positif. Faites du diviseur un nombre entier en « déplaçant » la virgule complètement vers la droite. « Déplacez » la virgule décimale du dividende du même nombre de places. 
Diviser. Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende. 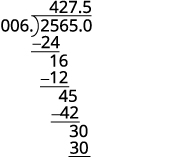
Écrivez le quotient avec le signe approprié. 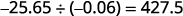
Diviser :\(−23.492÷(−0.04)\).
- Réponse
-
\(587.3\)
Diviser :\(−4.11÷(−0.12)\).
- Réponse
-
\(34.25\)
Convertir des nombres décimaux, des fractions et des pourcentages
Dans notre travail, il est souvent nécessaire de modifier la forme d'un nombre. Il se peut que nous devions changer les fractions en décimales ou les décimales en pourcentage.
Nous convertissons les décimales en fractions en identifiant la valeur de position du dernier chiffre (le plus à droite). Dans la décimale 0,03, le 3 est à la centième place, donc 100 est le dénominateur de la fraction équivalente à 0,03.
\[0.03=\dfrac{3}{100}\]
Les étapes à suivre pour convertir une décimale en fraction sont résumées dans l'encadré de procédure.
- Pour convertir une décimale en fraction appropriée, déterminez la valeur de position du dernier chiffre.
- Écrivez la fraction.
- numérateur : les « nombres » à droite de la virgule décimale
- dénominateur : valeur de position correspondant au dernier chiffre
- Pour convertir une fraction en décimal, divisez le numérateur de la fraction par le dénominateur de la fraction.
Ecrivez : ⓐ\(0.374\) sous forme de fraction ⓑ\(−\frac{5}{8}\) sous forme décimale.
- Réponse
-
ⓐ
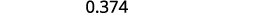
Déterminez la valeur de position du dernier chiffre. 
Écrivez la fraction pour 0,374 : le numérateur est 374. Le dénominateur est 1 000. 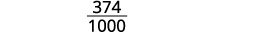
Simplifiez la fraction. 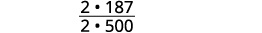
Répartissez les facteurs communs. 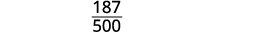
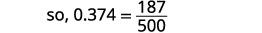
ⓑ Comme une barre de fraction signifie division, nous commençons par écrire la fraction\(\frac{5}{8}\) sous la forme\(8\sqrt{5}\). Maintenant, divisez.
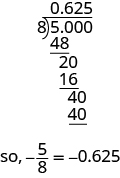
Ecrivez : ⓐ\(0.234\) sous forme de fraction ⓑ\(−\frac{7}{8}\) sous forme décimale.
- Réponse
-
ⓐ\(\frac{117}{500}\) ⓑ\(−0.875\)
Ecrivez : ⓐ\(0.024\) sous forme de fraction ⓑ\(−\frac{3}{8}\) sous forme décimale.
- Réponse
-
ⓐ\(\frac{3}{125}\) ⓑ\(−0.375\)
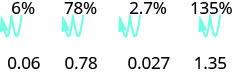
Un pourcentage est un ratio dont le dénominateur est 100. Le pourcentage signifie par cent. Nous utilisons le symbole du pourcentage, %, pour afficher le pourcentage. Comme un pourcentage est un ratio, il peut facilement être exprimé sous forme de fraction. Le pourcentage signifie pour 100, donc le dénominateur de la fraction est 100. Nous changeons ensuite la fraction en décimale en divisant le numérateur par le dénominateur. Après avoir fait cela plusieurs fois, vous pouvez voir le schéma.
Pour convertir un pourcentage en nombre décimal, nous déplaçons la virgule décimale de deux places vers la gauche.
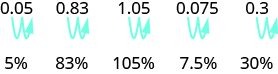
Pour convertir une décimale en pourcentage, n'oubliez pas que le pourcentage signifie pour cent. Si nous changeons la décimale en une fraction dont le dénominateur est 100, il est facile de changer cette fraction en pourcentage. Après de nombreuses conversions, vous pouvez reconnaître le modèle.
Pour convertir une décimale en pourcentage, nous déplaçons la virgule décimale de deux places vers la droite, puis nous ajoutons le signe du pourcentage.
- Pour convertir un pourcentage en décimal, déplacez la virgule décimale de deux places vers la gauche après avoir supprimé le signe du pourcentage.
- Pour convertir une décimale en pourcentage, déplacez la virgule décimale de deux places vers la droite, puis ajoutez le signe du pourcentage.
Convertissez chacun :
ⓐ pourcentage à une décimale : 62 %, 135 % et 13,7 %.
ⓑ décimal en pourcentage : 0,51, 1,25 et 0,093.
- Réponse
-
ⓐ
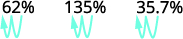
Déplace la virgule décimale de deux places vers la gauche. 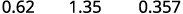
ⓑ
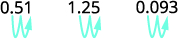
Déplacez la virgule décimale de deux places vers la droite. 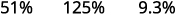
Convertissez chacun :
ⓐ pourcentage à une décimale : 9 %, 87 % et 3,9 %.
ⓑ décimal à un pourcentage : 0,17, 1,75 et 0,0825.
- Réponse
-
ⓐ 0,09, 0,87, 0,039 ⓑ 17 %, 175 %, 8,25 %
Convertissez chacun :
ⓐ pourcentage à une décimale : 3 %, 91 % et 8,3 %.
ⓑ décimal en pourcentage : 0,41, 2,25 et 0,0925.
- Réponse
-
ⓐ 0,03, 0,91, 0,083 ⓑ 41 %, 225 %, 9,25 %
Simplifiez les expressions avec des racines
N'oubliez pas que lorsqu'un nombre\(n\) est multiplié par lui-même, nous l'écrivons\(n^2\) et le lisons «\(n\) au carré ». Le résultat est appelé le carré d'un nombre n. Par exemple,\(\frac{8}{2}\) on lit « 8 au carré » et 64 est appelé le carré de 8. De même, 121 est le carré de 11 car\(11^2\) c'est 121. Il sera utile d'apprendre à reconnaître les nombres carrés parfaits.
Si\(n^2=m\), alors m est le carré de n.
Qu'en est-il des carrés de nombres négatifs ? Nous savons que lorsque les signes de deux nombres sont identiques, leur produit est positif. Ainsi, le carré de tout nombre négatif est également positif.
\[(−3)^2=9 \; \; \; \; \; \; \; \; \; (−8)^2=64 \; \; \; \; \; \; \; \; \; (−11)^2=121 \; \; \; \; \; \; \; \; \; (−15)^2=225\]
Parce\(10^2=100\) que nous disons que 100 est le carré de 10. Nous disons également que 10 est une racine carrée de 100. Un nombre dont le carré est m est appelé racine carrée d'un nombre m.
Si\(n^2=m\), alors n est la racine carrée de m.
Notez\((−10)^2=100\) également que −10 est également une racine carrée de 100. Par conséquent, 10 et −10 sont des racines carrées de 100. Ainsi, chaque nombre positif a deux racines carrées : une positive et une négative. Le signe radical,\(\sqrt{m}\), indique la racine carrée positive. La racine carrée positive est appelée racine carrée principale. Lorsque nous utilisons le signe radical, cela signifie toujours que nous voulons la racine carrée principale.
\(\sqrt{m}\)se lit comme suit : « la racine carrée de mm ».
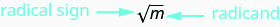
Si\(m=n^2\), alors\(\sqrt{m}=n\), pour\(n≥0\).
La racine carrée de m,\(\sqrt{m}\), est le nombre positif dont le carré est m.
Nous savons que chaque nombre positif a deux racines carrées et que le signe radical indique la racine positive. Nous écrivons\(\sqrt{100}=10\). Si nous voulons trouver la racine carrée négative d'un nombre, nous plaçons un négatif devant le signe radical. Par exemple,\(−\sqrt{100}=−10\). Nous nous lisons\(−\sqrt{100}\) comme « l'opposé de la racine carrée principale de 10 ».
Simplifier : ⓐ\(\sqrt{25}\) ⓑ\(\sqrt{121}\) ⓒ\(−\sqrt{144}\).
- Réponse
-
ⓐ
\(\begin{array}{ll} \text{} & \sqrt{25} \\ \text{Since }5^2=25 & 5 \end{array}\)ⓑ
\(\begin{array}{ll} \text{} & \sqrt{121} \\ \text{Since }11^2=121 & 11 \end{array}\)
ⓒ
\(\begin{array}{ll} {} & −\sqrt{144} \\ \text{The negative is in front of} & −12 \\ \text{the radical sign.} \end{array}\)
Simplifier : ⓐ\(\sqrt{36}\) ⓑ\(\sqrt{169}\) ⓒ\(−\sqrt{225}\)
- Réponse
-
ⓐ 6 ⓑ 13 ⓒ −15
Simplifier : ⓐ\(\sqrt{16}\) ⓑ\(\sqrt{196}\) ⓒ\(−\sqrt{100}\)
- Réponse
-
ⓐ 4 ⓑ 14 ⓒ −10
Identifier les entiers, les nombres rationnels, les nombres irrationnels et les nombres réels
Nous avons déjà décrit les nombres comme comptant le nombre s, le nombre entier s et les entiers. Quelle est la différence entre ces types de chiffres ? La différence peut être confondue avec la soustraction. Pourquoi ne pas nous demander comment nous distinguons ces types de nombres ?
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3,4,….. \\ \text{Whole numbers} & 0,1,2,3,4,…. \\ \text{Integers} & ….−3,−2,−1,0,1,2,3,…. \end{array}\]
Quel type de nombres obtiendrions-nous si nous commencions par tous les entiers et que nous incluions ensuite toutes les fractions ? Les nombres que nous aurions forment l'ensemble des nombres rationnels. Un nombre rationnel est un nombre qui peut être écrit sous la forme d'un ratio de deux entiers.
En général, toute décimale qui se termine après un certain nombre de chiffres (par exemple 7,3 ou −1,2684) est un nombre rationnel. Nous pouvons utiliser la valeur de position du dernier chiffre comme dénominateur lors de l'écriture de la décimale sous forme de fraction. La décimale pour\(\frac{1}{3}\) est le nombre\(0.\overline{3}\). La barre au-dessus du 3 indique que le chiffre 3 se répète à l'infini. Continuité a une signification importante dans le calcul. Le ou les chiffres situés sous la barre sont appelés blocs de répétition et ils se répètent en continu.
Comme tous les entiers peuvent être écrits sous la forme d'une fraction dont le dénominateur est 1, les entiers (et donc aussi le comptage et les nombres entiers) sont des nombres rationnels.
Chaque nombre rationnel peut être écrit à la fois comme un ratio d'entiers\(\frac{p}{q}\), où p et q sont des nombres entiers et\(q≠0\), comme une décimale qui s'arrête ou se répète.
Un nombre rationnel est un nombre de la forme\(\frac{p}{q}\), où p et q sont des nombres entiers et\(q≠0\).
Sa forme décimale s'arrête ou se répète.
Y a-t-il des décimales qui ne s'arrêtent pas ou ne se répètent pas ? Oui ! Le nombre ππ (la lettre grecque pi, prononcée « pie »), qui est très important pour décrire les cercles, a une forme décimale qui ne s'arrête pas et ne se répète pas. Nous utilisons trois points (...) pour indiquer que la décimale ne s'arrête pas ou ne se répète pas.
\[π=3.141592654...\]
La racine carrée d'un nombre qui n'est pas un carré parfait est une décimale qui ne s'arrête pas et ne se répète pas.
Un nombre dont la forme décimale ne s'arrête pas ou ne se répète pas ne peut pas être écrit sous forme de fraction d'entiers. C'est ce que nous appelons un numéro irrationnel.
Un nombre irrationnel est un nombre qui ne peut pas être écrit comme le ratio de deux entiers.
Sa forme décimale ne s'arrête pas et ne se répète pas.
Résumons une méthode que nous pouvons utiliser pour déterminer si un nombre est rationnel ou irrationnel.
Si la forme décimale d'un nombre
- se répète ou s'arrête, le nombre est un nombre rationnel.
- ne se répète pas et ne s'arrête pas, le nombre est un nombre irrationnel.
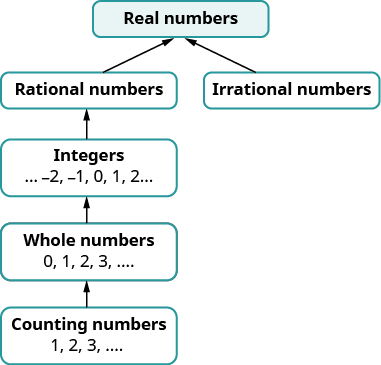
Nous avons vu que tous les nombres de comptage sont des nombres entiers, que tous les nombres entiers sont des entiers et que tous les nombres entiers sont des nombres rationnels. Les nombres irrationnels sont des nombres dont la forme décimale ne s'arrête pas et ne se répète pas. Lorsque nous réunissons les nombres rationnels et les nombres irrationnels, nous obtenons l'ensemble des nombres réels s.
Un nombre réel est un nombre rationnel ou irrationnel.
Plus loin dans ce cours, nous introduirons des nombres au-delà des nombres réels. La figure montre comment les ensembles de numéros que nous avons utilisés jusqu'à présent s'imbriquent.
Le terme « nombres réels » vous semble étrange ? Y a-t-il des chiffres qui ne sont pas « réels » et, dans l'affirmative, quels pourraient-ils être ? Pouvons-nous simplifier\(−\sqrt{25}\) ? Y a-t-il un nombre dont le carré est\(−25\) ?
\[()^2=−25?\]
Aucun des chiffres que nous avons traités jusqu'à présent n'a de carré\(−25\). Pourquoi ? Tout nombre positif au carré est positif. Tout nombre négatif au carré est positif. Nous disons donc qu'il n'y a pas de nombre réel égal à\(\sqrt{−25}\). La racine carrée d'un nombre négatif n'est pas un nombre réel.
Compte tenu des nombres\(−7,\frac{14}{5},8,\sqrt{5},5.9,−\sqrt{64}\), listez les ⓐ nombres entiers ⓑ nombres entiers ⓒ nombres rationnels ⓓ nombres irrationnels ⓔ nombres réels.
- Réponse
-
ⓐ N'oubliez pas que les nombres entiers sont\(0,1,2,3,…,\) donc 8 est le seul nombre entier donné.
ⓑ Les entiers sont les nombres entiers et leurs contraires (y compris 0). Donc, le nombre entier 8 est un entier, et −7 est l'opposé d'un nombre entier, donc c'est aussi un entier. Notez également que 64 est le carré de 8 donc\(−\sqrt{64}=−8\). Les nombres entiers sont donc\(−7,8,\) et\(−\sqrt{64}\).
ⓒ Puisque tous les entiers sont rationnels, alors\(−7,8,\) et\(−\sqrt{64}\) sont rationnels. Les nombres rationnels incluent également les fractions et les décimales qui se répètent ou s'arrêtent, donc\(\frac{14}{5}\) et\(5.9\) sont rationnels. La liste des nombres rationnels est donc\(−7,\frac{14}{5},8,5.9,\) et\(−\sqrt{64}\).
ⓓ N'oubliez pas que 5 n'est pas un carré parfait,\(\sqrt{5}\) c'est donc irrationnel.
ⓔ Tous les nombres listés sont des nombres réels.
Étant donné les nombres,\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49},\) listez les ⓐ nombres entiers ⓑ nombres entiers ⓒ nombres rationnels
ⓓ nombres irrationnels ⓔ nombres réels.
- Réponse
-
ⓐ\(4,\sqrt{49}\) ⓑ\(−3,4,\sqrt{49}\)
ⓒ\(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) ⓓ\(−\sqrt{2}\)ⓔ\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)
Les nombres donnés\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\) listent les ⓐ nombres entiers ⓑ entiers ⓒ nombres rationnels ⓓ nombres irrationnels ⓔ nombres réels.
- Réponse
-
ⓐ\(6,\sqrt{121}\)
ⓑ\(−\sqrt{25},−1,6,\sqrt{121}\)
ⓒ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)
ⓓ\(2.041975...\)
ⓔ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)
Localisez les fractions et les décimales sur la ligne numérique
Nous voulons maintenant inclure des fractions et des décimales sur la ligne numérique. Commençons par les fractions et localisons\(\frac{1}{5},−\frac{4}{5},3,\frac{7}{4},−\frac{9}{2},−5\) et\(\frac{8}{3}\) sur la ligne numérique.
Nous allons commencer par les nombres entiers 3 et −5 car ce sont les plus faciles à tracer. Voir la figure.
Les fractions appropriées répertoriées sont\(\frac{1}{5}\) et\(−\frac{4}{5}.\) nous savons que la fraction appropriée\(\frac{1}{5}\) a une valeur inférieure à un et serait donc située entre 0 et 1. Le dénominateur est 5, nous divisons donc l'unité de 0 à 1 en 5 parties égales\(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\). Nous complotons\(\frac{1}{5}\).
De même,\(−\frac{4}{5}\) est compris entre 0 et -1. Après avoir divisé l'unité en 5 parties égales, nous tracons\(−\frac{4}{5}\).
Enfin, examinez les fractions inappropriées\(\frac{7}{4},\frac{9}{2},\frac{8}{3}\). Il peut être plus facile de localiser ces points si vous remplacez chacun d'eux par un nombre mixte.
\[\dfrac{7}{4}=1\dfrac{3}{4} \; \; \; \; \; \; \; \; \; −\dfrac{9}{2}=−4\dfrac{1}{2} \; \; \; \; \; \; \; \; \; \dfrac{8}{3}=2\dfrac{2}{3}\]
La figure montre la ligne numérique avec tous les points tracés.

Localisez et étiquetez les éléments suivants sur une ligne numérique :\(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\) et\(\frac{7}{3}\).
- Réponse
-
Localisez et tracez les nombres entiers,\(4,−3.\)
Trouvez d'\(\frac{3}{4}\)abord la fraction appropriée. La fraction\(\frac{3}{4}\) est comprise entre 0 et 1. Divisez la distance entre 0 et 1 en quatre parties égales, puis nous tracons\(\frac{3}{4}\). Diagramme similaire\(−\frac{1}{4}\).
Localisez maintenant les fractions inappropriées\(\frac{6}{5},−\frac{5}{2},\) et\(\frac{7}{3}\). Il est plus facile de les tracer si nous les convertissons en nombres mixtes, puis les traçons comme décrit ci-dessus :\(\frac{6}{5}=1\frac{1}{5},−\frac{5}{2}=−2\frac{1}{2},\frac{7}{3}=2\frac{1}{3}\).

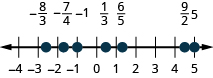
Localisez et étiquetez les éléments suivants sur une ligne numérique :\(−1,\frac{1}{3},\frac{6}{5},−\frac{7}{4},\frac{9}{2},5,−\frac{8}{3}\).
- Réponse
-
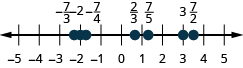
Localisez et étiquetez les éléments suivants sur une ligne numérique :\(−2,\frac{2}{3},\frac{7}{5},−\frac{7}{4},\frac{7}{2},3,−\frac{7}{3}\).
- Réponse
-
Les décimales étant des formes de fractions, la localisation des décimales sur la ligne numérique est similaire à la localisation des fractions sur la ligne numérique.
Localisez sur la ligne numérique : ⓐ 0,4 ⓑ −0,74.
- Réponse
-
ⓐ Le nombre décimal 0,4 est équivalent à\(\frac{4}{10}\) une fraction propre, donc 0,4 est situé entre 0 et 1. Sur une ligne numérique, divisez l'intervalle entre 0 et 1 en 10 parties égales. Maintenant, étiquetez les pièces 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7, 0,8, 0,9, 1,0. Nous écrivons 0 comme 0,0 et 1 comme 1,0, afin que les nombres soient toujours en dixièmes. Enfin, marquez 0,4 sur la ligne numérique.

ⓑ La décimale\(−0.74\) est équivalente à\(−\frac{74}{100}\), elle est donc située entre 0 et .−1. Sur une ligne numérique, cochez et étiquetez les centièmes de l'intervalle compris entre 0 et −1.

Localisez sur la ligne numérique : ⓐ\(0.6\) ⓑ\(−0.25.\)
- Réponse
-
ⓐ

ⓑ
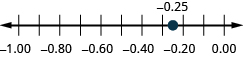
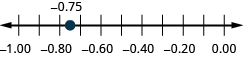
Localisez sur la ligne numérique : ⓐ 0,90,9 ⓑ −0,75 −0,75.
- Réponse
-
ⓐ

ⓑ
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les décimales.
- Principes de base de l'arithmétique : division de décimales
Concepts clés
- Comment arrondir les décimales.
- Localisez la valeur de position donnée et marquez-la avec une flèche.
- Soulignez le chiffre situé à droite de la valeur de la position.
- Le chiffre souligné est-il supérieur ou égal à 5 ?
- Oui : ajoutez 1 au chiffre dans la valeur de position donnée.
- Non : ne modifiez pas le chiffre dans la valeur de position indiquée
- Réécrivez le nombre en supprimant tous les chiffres situés à droite du chiffre arrondi.
- Comment ajouter ou soustraire des décimales
- Déterminez le signe de la somme ou de la différence.
- Écrivez les nombres de manière à ce que les décimales soient alignées verticalement.
- Utilisez des zéros comme espaces réservés, selon les besoins.
- Ajoutez ou soustrayez les nombres comme s'il s'agissait de nombres entiers. Placez ensuite le point décimal dans la réponse sous les décimales des nombres donnés.
- Écrivez la somme ou la différence avec le signe approprié
- Comment multiplier les décimales.
- Déterminez le signe du produit.
- Écrivez au format vertical en alignant les chiffres sur la droite. Multipliez les nombres comme s'ils étaient des nombres entiers, en ignorant temporairement les décimales.
- Placez le point décimal. Le nombre de décimales dans le produit est la somme du nombre de décimales des facteurs.
- Écrivez le produit avec le signe approprié.
- Comment multiplier une décimale par une puissance de dix.
- Déplacez la virgule décimale vers la droite autant de places que le nombre de zéros de la puissance 10.
- Ajoutez des zéros à la fin du numéro si nécessaire.
- Comment diviser les décimales.
- Déterminez le signe du quotient.
- Faites du diviseur un nombre entier en « déplaçant » la virgule complètement vers la droite. « Déplacez » la virgule décimale du dividende du même nombre de positions, en ajoutant des zéros si nécessaire.
- Diviser. Placez la virgule décimale dans le quotient au-dessus de la virgule décimale du dividende.
- Écrivez le quotient avec le signe approprié.
- Comment convertir une décimale en fraction appropriée et une fraction en décimal.
- Pour convertir une décimale en fraction appropriée, déterminez la valeur de position du dernier chiffre.
- Écrivez la fraction.
- numérateur : les « nombres » à droite de la virgule décimale
- dénominateur : valeur de position correspondant au dernier chiffre
- Pour convertir une fraction en décimal, divisez le numérateur de la fraction par le dénominateur de la fraction.
- Comment convertir un pourcentage en décimal et un décimal en pourcentage.
- Pour convertir un pourcentage en décimal, déplacez la virgule décimale de deux places vers la gauche après avoir supprimé le signe du pourcentage.
- Pour convertir une décimale en pourcentage, déplacez la virgule décimale de deux places vers la droite, puis ajoutez le signe du pourcentage.
- La notation à racine carrée\(\sqrt{m}\) se lit comme suit : « la racine carrée de m ». Si\(m=n^2\), alors\(\sqrt{m}=n\), pour\(n≥0\). La racine carrée de m,\(\sqrt{m}\), est le nombre positif dont le carré est m.
- Rationnel ou irrationnel Si la forme décimale d'un nombre
- se répète ou s'arrête, le nombre est un nombre rationnel.
- ne se répète pas et ne s'arrête pas, le nombre est un nombre irrationnel.
- Nombres réels
.jpg)
Graphique 4.
Lexique
- nombre irrationnel
- Un nombre irrationnel est un nombre qui ne peut pas être écrit comme le ratio de deux entiers. Sa forme décimale ne s'arrête pas et ne se répète pas.
- pour cent
- Un pourcentage est un ratio dont le dénominateur est 100.
- racine carrée principale
- La racine carrée positive est appelée racine carrée principale.
- numéro rationnel
- Un nombre rationnel est un nombre de la forme\(\frac{p}{q}\), où p et q sont des nombres entiers et\(q≠0\). Sa forme décimale s'arrête ou se répète.
- nombre réel
- Un nombre réel est un nombre rationnel ou irrationnel.
- carré d'un nombre
- Si\(n^2=m\), alors m est le carré de n.
- racine carrée d'un nombre
- Si\(n^2=m\), alors n est la racine carrée de m.


