Skip to main content
Global

1.4E : Exercices

  1. Last updated
  2. Save as PDF
  • Page ID
    194234

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique rend parfait

    Simplifier les

    Dans les exercices suivants, simplifiez.

    1. \(−\dfrac{108}{63}\)

    Réponse

    \(−\dfrac{12}{7}\)

    2. \(−\dfrac{104}{48}\)

    3. \(\dfrac{120}{252}\)

    Réponse

    \(\dfrac{10}{21}\)

    4. \(\dfrac{182}{294}\)

    5. \(\dfrac{14x^2}{21y}\)

    Réponse

    \(\dfrac{2x^2}{3y}\)

    6. \(\dfrac{24a}{32b^2}\)

    7. \(−\dfrac{210a^2}{110b^2}\)

    Réponse

    \(−\dfrac{21a^2}{11b^2}\)

    8. \(−\dfrac{30x^2}{105y^2}\)

    Multiplier et diviser des fractions

    Dans les exercices suivants, effectuez l'opération indiquée.

    9. \(−\dfrac{3}{4}\left(−\dfrac{4}{9}\right)\)

    Réponse

    \(\dfrac{1}{3}\)

    10. \(−\dfrac{3}{8}⋅\dfrac{4}{15}\)

    11. \(\left(−\dfrac{14}{15}\right)\left(\dfrac{9}{20}\right)\)

    Réponse

    \(−\dfrac{21}{50}\)

    12. \(\left(−\dfrac{9}{10}\right)\left(\dfrac{25}{33}\right)\)

    13. \(\left(−\dfrac{63}{84}\right)\left(−\dfrac{44}{90}\right)\)

    Réponse

    \(\dfrac{11}{30}\)

    14. \(\left(−\dfrac{33}{60}\right)\left(−\dfrac{40}{88}\right)\)

    15. \(\dfrac{3}{7}⋅21n\)

    Réponse

    \(9n\)

    16. \(\dfrac{5}{6}⋅30m\)

    17. \(\dfrac{3}{4}÷\dfrac{x}{11}\)

    Réponse

    \(\dfrac{33}{4x}\)

    18. \(\dfrac{2}{5}÷\dfrac{y}{9}\)

    19. \(\dfrac{5}{18}÷\left(−\dfrac{15}{24}\right)\)

    Réponse

    \(−\dfrac{4}{9}\)

    20. \(\dfrac{7}{18}÷\left(−\dfrac{14}{27}\right)\)

    21. \(\dfrac{8u}{15}÷\dfrac{12v}{25}\)

    Réponse

    \(\dfrac{10u}{9v}\)

    22. \(\dfrac{12r}{25}÷\dfrac{18s}{35}\)

    23. \(\dfrac{3}{4}÷(−12)\)

    Réponse

    \(−\dfrac{1}{16}\)

    24. \(−15÷\left(−\dfrac{5}{3}\right)\)

    Dans les exercices suivants, simplifiez.

    25. \(−\dfrac{\dfrac{8}{21} }{\dfrac{12}{35}}\)

    Réponse

    \(−\dfrac{10}{9}\)

    26. \(− \dfrac{\dfrac{9}{16} }{\dfrac{33}{40}}\)

    27. \(−\dfrac{\dfrac{4}{5}}{2}\)

    Réponse

    \(−\dfrac{2}{5}\)

    28. \(\dfrac{\dfrac{5}{3}}{10}\)

    29. \(\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}\)

    Réponse

    \(\dfrac{2m}{3n}\)

    30. \(\dfrac{−\dfrac{3}{8}}{−\dfrac{y}{12}}\)

    Ajouter et soustraire des fractions

    Dans les exercices suivants, ajoutez ou soustrayez.

    31. \(\dfrac{7}{12}+\dfrac{5}{8}\)

    Réponse

    \(\dfrac{29}{24}\)

    32. \(\dfrac{5}{12}+\dfrac{3}{8}\)

    33. \(\dfrac{7}{12}−\dfrac{9}{16}\)

    Réponse

    \(\dfrac{1}{48}\)

    34. \(\dfrac{7}{16}−\dfrac{5}{12}\)

    35. \(−\dfrac{13}{30}+\dfrac{25}{42}\)

    Réponse

    \(\dfrac{17}{105}\)

    36. \(−\dfrac{23}{30}+\dfrac{5}{48}\)

    37. \(−\dfrac{39}{56}−\dfrac{22}{35}\)

    Réponse

    \(−\dfrac{53}{40}\)

    38. \(−\dfrac{33}{49}−\dfrac{18}{35}\)

    39. \(−\dfrac{2}{3}−\left(−\dfrac{3}{4}\right)\)

    Réponse

    \(\dfrac{1}{12}\)

    40. \(−\dfrac{3}{4}−\left(−\dfrac{4}{5}\right)\)

    41. \(\dfrac{x}{3}+\dfrac{1}{4}\)

    Réponse

    \(\dfrac{4x+3}{12}\)

    42. \(\dfrac{x}{5}−\dfrac{1}{4}\)

    43. ⓐ\(\dfrac{2}{3}+\dfrac{1}{6}\)

    ⓑ\(\dfrac{2}{3}÷\dfrac{1}{6}\)

    Réponse

    ⓐ\(\dfrac{5}{6}\) ⓑ\(4\)

    44. ⓐ\(−\dfrac{2}{5}−\dfrac{1}{8}\)

    ⓑ\(−\dfrac{2}{5}·\dfrac{1}{8}\)

    45. ⓐ\(\dfrac{5n}{6}÷\dfrac{8}{15}\)

    ⓑ\(\dfrac{5n}{6}−\dfrac{8}{15}\)

    Réponse

    ⓐ\(\dfrac{25n}{16}\) ⓑ\(\dfrac{25n−16}{30}\)

    46. ⓐ\(\dfrac{3a}{8}÷\dfrac{7}{12}\)

    ⓑ\(\dfrac{3a}{8}−\dfrac{7}{12}\)

    47. ⓐ\(−\dfrac{4x}{9}−\dfrac{5}{6}\)

    ⓑ\(−\dfrac{4k}{9}⋅\dfrac{5}{6}\)

    Réponse

    ⓐ\(\dfrac{−8x−15}{18}\) ⓑ\(−\dfrac{10k}{27}\)

    48. ⓐ\(−\dfrac{3y}{8}−\dfrac{4}{3}\)

    ⓑ\(−\dfrac{3y}{8}⋅\dfrac{4}{3}\)

    49. ⓐ\(−\dfrac{5a}{3}+\left(−\dfrac{10}{6}\right)\)

    ⓑ\(−\dfrac{5a}{3}÷\left(−\dfrac{10}{6}\right)\)

    Réponse

    ⓐ\(\dfrac{−5(a+1)}{3}\) ⓑ\(a\)

    50. ⓐ\(\dfrac{2b}{5}+\dfrac{8}{15}\)

    ⓑ\(\dfrac{2b}{5}÷\dfrac{8}{15}\)

    Utiliser l'ordre des opérations pour simplifier les fractions

    Dans les exercices suivants, simplifiez.

    51. \(\dfrac{5⋅6−3⋅4}{4⋅5−2⋅3}\)

    Réponse

    \(\dfrac{9}{7}\)

    52. \(\dfrac{8⋅9−7⋅6}{5⋅6−9⋅2}\)

    53. \(\dfrac{5^2−3^2}{3−5}\)

    Réponse

    \(−8\)

    54. \(\dfrac{6^2−4^2}{4−6}\)

    55. \(\dfrac{7⋅4−2(8−5)}{9⋅3−3⋅5}\)

    Réponse

    \(\dfrac{11}{6}\)

    56. \(\dfrac{9⋅7−3(12−8)}{8⋅7−6⋅6}\)

    57. \(\dfrac{9(8−2)−3(15−7)}{6(7−1)−3(17−9)}\)

    Réponse

    \(\dfrac{5}{2}\)

    58. \(\dfrac{8(9−2)−4(14−9)}{7(8−3)−3(16−9)}\)

    59. \(\dfrac{2^3+4^2}{\left(\dfrac{2}{3}\right)^2}\)

    Réponse

    \(54\)

    60. \(\dfrac{3^3−3^2}{\left(\dfrac{3}{4}\right)^2}\)

    61. \(\dfrac{\left(\dfrac{3}{5}\right)^2}{\left(\dfrac{3}{7}\right)^2}\)

    Réponse

    \(\dfrac{49}{25}\)

    62. \(\dfrac{\left(\dfrac{3}{4}\right)^2}{\left(\dfrac{5}{8}\right)^2}\)

    63. \(\dfrac{2}{\dfrac{1}{3}+\dfrac{1}{5}}\)

    Réponse

    \(\dfrac{15}{4}\)

    64. \(\dfrac{5}{\dfrac{1}{4}+\dfrac{1}{3}}\)

    65. \(\dfrac{\dfrac{7}{8}−\dfrac{2}{3}}{\dfrac{1}{2}+\dfrac{3}{8}}\)

    Réponse

    \(\dfrac{5}{21}\)

    66. \(\dfrac{\dfrac{3}{4}−\dfrac{3}{5}}{\dfrac{1}{4}+\dfrac{2}{5}}\)

    Pratique mixte

    Dans les exercices suivants, simplifiez.

    67. \(−\dfrac{3}{8}÷\left(−\dfrac{3}{10}\right)\)

    Réponse

    \(\dfrac{5}{4}\)

    68. \(−\dfrac{3}{12}÷\left(−\dfrac{5}{9}\right)\)

    69. \(−\dfrac{3}{8}+\dfrac{5}{12}\)

    Réponse

    \(\dfrac{1}{24}\)

    70. \(−\dfrac{1}{8}+\dfrac{7}{12}\)

    71. \(−\dfrac{7}{15}−\dfrac{y}{4}\)

    Réponse

    \(\dfrac{−28−15y}{60}\)

    72. \(−\dfrac{3}{8}−\dfrac{x}{11}\)

    73. \(\dfrac{11}{12a}⋅\dfrac{9a}{16}\)

    Réponse

    \(\dfrac{33}{64}\)

    74. \(\dfrac{10y}{13}⋅\dfrac{8}{15y}\)

    75. \(\dfrac{1}{2}+\dfrac{2}{3}⋅\dfrac{5}{12}\)

    Réponse

    \(\dfrac{7}{9}\)

    76. \(\dfrac{1}{3}+\dfrac{2}{5}⋅\dfrac{3}{4}\)

    77. \(1−\dfrac{3}{5}÷\dfrac{1}{10}\)

    Réponse

    \(−5\)

    78. \(1−\dfrac{5}{6}÷\dfrac{1}{12}\)

    79. \(\dfrac{3}{8}−\dfrac{1}{6}+\dfrac{3}{4}\)

    Réponse

    \(\dfrac{23}{24}\)

    80. \(\dfrac{2}{5}+\dfrac{5}{8}−\dfrac{3}{4}\)

    81. \(12\left(\dfrac{9}{20}−\dfrac{4}{15}\right)\)

    Réponse

    \(\dfrac{11}{5}\)

    82. \(8\left(\dfrac{15}{16}−\dfrac{5}{6}\right)\)

    83. \(\dfrac{\dfrac{5}{8}+\dfrac{1}{6}}{\dfrac{19}{24}}\)

    Réponse

    \(1\)

    84. \(\dfrac{\dfrac{1}{6}+\dfrac{3}{10}}{\dfrac{14}{30}}\)

    ​​​​​​​

    85. \(\left(\dfrac{5}{9}+\dfrac{1}{6}\right)÷\left(\dfrac{2}{3}−\dfrac{1}{2}\right)\)

    Réponse

    \(\dfrac{13}{3}\)

    86. \(\left(\dfrac{3}{4}+\dfrac{1}{6}\right)÷\left(\dfrac{5}{8}−\dfrac{1}{3}\right)\)

    Évaluer des expressions variables avec des fractions

    Dans les exercices suivants, évaluez.

    87. \(\dfrac{7}{10}−w\)quand ⓐ\(w=\dfrac{1}{2}\) ⓑ\(w=−\dfrac{1}{2}\)

    Réponse

    ⓐ\(\dfrac{1}{5}\) ⓑ\(\dfrac{6}{5}\)

    88. \(512−w\)quand ⓐ\(w=\dfrac{1}{4}\) ⓑ\(w=−\dfrac{1}{4}\)

    ​​​​​​​​​​​​​​

    89. \(2x^2y^3\)quand\(x=−\dfrac{2}{3}\) et\(y=−\dfrac{1}{2}\)

    Réponse

    \(−\dfrac{1}{9}\)

    90. \(8u^2v^3\)quand\(u=−\dfrac{3}{4}\) et\(v=−\dfrac{1}{2}\)

    ​​​​​​​​​​​​​​

    91. \(\dfrac{a+b}{a−b}\)quand\(a=−3\) et\(b=8\)

    Réponse

    \(−\dfrac{5}{11}\)

    92. \(\dfrac{r−s}{r+s}\)quand\(r=10\) et\(s=−5\)

    Exercices d'écriture

    93. Pourquoi avez-vous besoin d'un dénominateur commun pour ajouter ou soustraire des fractions ? Expliquez.

    Réponse

    Les réponses peuvent varier.

    94. Comment trouvez-vous l'écran LCD de 2 fractions ?

    95. Expliquez comment vous trouvez l'inverse d'une fraction.

    Réponse

    Les réponses peuvent varier.

    96. Expliquez comment vous trouvez l'inverse d'un nombre négatif.

    Auto-vérification

    ⓐ Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

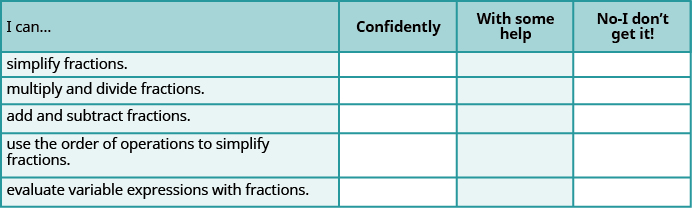
    Ce tableau comporte 4 colonnes, 5 lignes et une ligne d'en-tête. La ligne d'en-tête étiquette chaque colonne que je peux, en toute confiance, avec de l'aide et non, je ne comprends pas. La première colonne contient les instructions suivantes : simplifier les fractions, multiplier et diviser des fractions, ajouter et soustraire des fractions, utiliser l'ordre des opérations pour simplifier les fractions, évaluer des expressions variables avec des fractions. Les colonnes restantes sont vides.

    ⓑ Que vous apprend cette liste de contrôle sur votre maîtrise de cette section ? Quelles mesures allez-vous prendre pour vous améliorer ?