1.4 : Fractions
- Page ID
- 194226
À la fin de cette section, vous serez en mesure de :
- Simplifier les
- Multiplier et diviser des fractions
- Ajouter et soustraire des fractions
- Utiliser l'ordre des opérations pour simplifier les fractions
- Évaluez des expressions variables avec des fractions
Une introduction plus complète aux sujets abordés dans cette section se trouve dans le chapitre sur l'algèbre élémentaire, Fondations.
Simplifier les
Une fraction est un moyen de représenter des parties d'un tout. La fraction\(\frac{2}{3}\) représente deux des trois parties égales (Figure\(\PageIndex{1}\)). Dans la fraction\(\frac{2}{3}\), le 2 est appelé numérateur et le 3 est appelé dénominateur. La ligne est appelée barre de fraction.
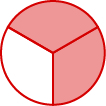
Figure\(\PageIndex{1}\) : Dans le cercle, 2\(\frac{2}{3}\) des 3 parties égales du cercle sont ombrées.
Une fraction est écrite\(\dfrac{a}{b}\), où\(b\neq 0\) et
\(a\)est le numérateur et\(b\) le dénominateur.
Une fraction représente des parties d'un tout. Le dénominateur\(b\) est le nombre de parties égales en lesquelles l'ensemble a été divisé, et le numérateur\(a\) indique le nombre de parties incluses.
Les fractions qui ont la même valeur sont des fractions équivalentes. Les fractions équivalentes
La propriété nous permet de trouver des fractions équivalentes et de simplifier les fractions.
Si\(a\)\(b\), et\(c\) sont des nombres où\(b\neq 0,c\neq 0\),
puis\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\) et\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
Une fraction est considérée comme simplifiée s'il n'existe aucun facteur commun, autre que 1, dans son numérateur et son dénominateur.
Par exemple,
\(\dfrac{2}{3}\)est simplifiée car il n'y a pas de facteurs communs entre\(2\) et\(3\).
\(\dfrac{10}{15}\)n'est pas simplifié car\(5\) c'est un facteur commun à\(10\) et\(15\).
Nous simplifions ou réduisons une fraction en supprimant les facteurs communs que sont le numérateur et le dénominateur. Une fraction n'est pas simplifiée tant que tous les facteurs communs n'ont pas été supprimés. Si une expression contient des fractions, elle n'est pas complètement simplifiée tant que les fractions ne sont pas simplifiées.
Parfois, il n'est pas facile de trouver les facteurs communs du numérateur et du dénominateur. Lorsque cela se produit, une bonne idée est de factoriser le numérateur et le dénominateur en nombres premiers. Divisez ensuite les facteurs communs à l'aide de la propriété des fractions équivalentes.
Simplifiez\(\dfrac{−315}{770}\).
- Réponse
-



Simplifiez\(−\dfrac{69}{120}\).
- Réponse
-
\(−\dfrac{23}{40}\)
Simplifiez\(−\dfrac{120}{192}\).
- Réponse
-
\(−\dfrac{5}{8}\)
Nous résumons maintenant les étapes à suivre pour simplifier les fractions.
- Réécrivez le numérateur et le dénominateur pour montrer les facteurs communs.
Au besoin, factorisez d'abord le numérateur et le dénominateur en nombres premiers. - Simplifiez l'utilisation de la propriété Fractions équivalentes en divisant les facteurs communs.
- Multipliez tous les facteurs restants.
Multiplier et diviser des fractions
De nombreuses personnes trouvent qu'il est plus facile de multiplier et de diviser des fractions que d'ajouter et de soustraire des fractions.
Pour multiplier les fractions, on multiplie les numérateurs et on multiplie les dénominateurs.
Si\(a\),\(b\)\(c\), et\(d\) sont des nombres où\(b≠0\), et\(d≠0\), alors
\[\frac{a}{b}·\frac{c}{d}=\frac{ac}{bd}\]
Pour multiplier les fractions, multipliez les numérateurs et multipliez les dénominateurs.
Lors de la multiplication de fractions, les propriétés des nombres positifs et négatifs s'appliquent toujours, bien entendu. C'est une bonne idée de déterminer le signe du produit dans un premier temps. Dans l'exemple, nous allons multiplier un négatif par un positif, de sorte que le produit sera négatif.
Lorsque vous multipliez une fraction par un entier, il peut être utile d'écrire l'entier sous forme de fraction. Tout entier, a, peut être écrit sous la forme\(\dfrac{a}{1}\). Ainsi, par exemple,\(3=\dfrac{3}{1}\).
Multipliez :\(−\dfrac{12}{5}(−20x).\)
- Réponse
-
La première étape consiste à trouver le signe du produit. Les signes étant les mêmes, le produit est positif.
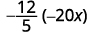
Déterminez le signe du produit. Les signes sont les mêmes, donc le produit est positif.
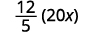
Ecrivez 20 x sous forme de fraction. 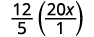
Multipliez. 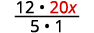
Réécrivez 20 pour afficher le facteur commun 5 et divisez-le.
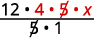
Simplifiez. 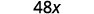
Multipliez :\(\dfrac{1}{13}(−9a)\).
- Réponse
-
\(−33a\)
Multipliez :\(\dfrac{13}{7}(−14b)\).
- Réponse
-
\(−26b\)
Maintenant que nous savons comment multiplier les fractions, nous sommes presque prêts à diviser. Avant de pouvoir le faire, nous avons besoin d'un peu de vocabulaire. L'inverse d'une fraction est trouvé en inversant la fraction, en plaçant le numérateur dans le dénominateur et le dénominateur dans le numérateur. La réciproque de l'\(\frac{2}{3}\)est\(\frac{3}{2}\). Puisque 4 est écrit sous forme de fraction comme\(\frac{4}{1}\), l'inverse de 4 l'est\(\frac{1}{4}\).
Pour diviser des fractions, on multiplie la première fraction par l'inverse de la seconde.
Si\(a\),\(b\)\(c\), et\(d\) sont des nombres où\(b≠0\)\(c≠0\), et\(d≠0\), alors
\[\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}⋅\frac{d}{c}\]
Pour diviser des fractions, on multiplie la première fraction par l'inverse de la seconde.
Nous devons dire\(b≠0\), et\(c≠0\)\(d≠0\), pour être sûrs de ne pas diviser par zéro !
Trouvez le quotient :\(−\dfrac{7}{18}÷(−\dfrac{14}{27}).\)
- Réponse
-
\(−\dfrac{7}{18}÷(−\dfrac{14}{27})\) Pour diviser, multipliez la première fraction par l'inverse de la seconde.
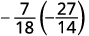
Déterminez le signe du produit, puis multipliez.
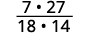
Réécrivez en indiquant les facteurs communs. 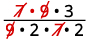
Supprimez les facteurs courants. 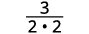
Simplifiez. 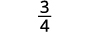
Diviser :\(−\dfrac{7}{27}÷(−\dfrac{35}{36})\).
- Réponse
-
\(\dfrac{4}{15}\)
Diviser :\(−\dfrac{5}{14}÷(−\dfrac{15}{28}).\)
- Réponse
-
\(\dfrac{2}{3}\)
Les numérateurs ou dénominateurs de certaines fractions contiennent eux-mêmes des fractions. Une fraction dont le numérateur ou le dénominateur est une fraction est appelée fraction complexe.
Une fraction complexe est une fraction dont le numérateur ou le dénominateur contient une fraction.
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{ \frac{5}{6}}\]
Pour simplifier une fraction complexe, n'oubliez pas que la barre de fraction signifie division. Par exemple, la fraction complexe\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) signifie\(\dfrac{3}{4}÷\frac{5}{8}.\)
Simplifiez :\(\dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}}\).
- Réponse
-
\(\begin{array}{lc} \text{} & \dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}} \\[6pt] \text{Rewrite as division.} & \dfrac{x}{2}÷\dfrac{xy}{6} \\[6pt] \text{Multiply the first fraction by the reciprocal of the second.} & \dfrac{x}{2}·\dfrac{6}{xy} \\[6pt] \text{Multiply.} & \dfrac{x·6}{2·xy} \\[6pt] \text{Look for common factors.} & \dfrac{ \cancel{x}·3·\cancel{2}}{\cancel{2}·\cancel{x}·y} \\[6pt] \text{Divide common factors and simplify.} & \dfrac{3}{y} \end{array}\)
Simplifiez :\(\dfrac{\dfrac{a}{8}}{ \dfrac{ab}{6}}\).
- Réponse
-
\(\dfrac{3}{4b}\)
Simplifiez :\(\dfrac{\dfrac{p}{2}}{ \dfrac{pq}{8}}\).
- Réponse
-
\(\dfrac{4}{q}\)
Ajouter et soustraire des fractions
Lorsque nous avons multiplié des fractions, nous avons simplement multiplié les numérateurs et multiplié les dénominateurs directement. Pour ajouter ou soustraire des fractions, elles doivent avoir un dénominateur commun.
Si\(a\)\(b\), et\(c\) sont des nombres où\(c≠0\), alors
\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\]
Pour ajouter ou soustraire des fractions, ajoutez ou soustrayez les numérateurs et placez le résultat au-dessus du dénominateur commun.
Le plus petit dénominateur commun (LCD) de deux fractions est le plus petit nombre pouvant être utilisé comme dénominateur commun des fractions. L'écran LCD des deux fractions est le plus petit multiple commun (LCM) de leurs dénominateurs.
Le plus petit dénominateur commun (LCD) de deux fractions est le plus petit multiple commun (LCM) de leurs dénominateurs.
Après avoir trouvé le plus petit dénominateur commun de deux fractions, nous convertissons les fractions en fractions équivalentes à l'aide de l'écran LCD. La combinaison de ces étapes nous permet d'additionner et de soustraire des fractions car leurs dénominateurs seront les mêmes !
Ajoutez :\(\dfrac{7}{12}+\dfrac{5}{18}\).
- Réponse
-



Ajoutez :\(\dfrac{7}{12}+\dfrac{11}{15}\).
- Réponse
-
\(\dfrac{79}{60}\)
Ajoutez :\(\dfrac{13}{15}+\dfrac{17}{20}\).
- Réponse
-
\(\dfrac{103}{60}\)
- Ont-ils un dénominateur commun ?
- Oui, passez à l'étape 2.
- NON : réécrivez chaque fraction à l'aide de l'écran LCD (le plus petit dénominateur commun).
- Trouvez l'écran LCD.
- Changez chaque fraction en une fraction équivalente avec l'écran LCD comme dénominateur.
- Ajoutez ou soustrayez les fractions.
- Simplifiez, si possible.
Nous avons maintenant les quatre opérations pour les fractions. Le tableau résume les opérations de fraction.
| Multiplication de | Division des fractions |
|---|---|
| \(\dfrac{a}{b}⋅\dfrac{c}{d}=\dfrac{ac}{bd}\) | \(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\) |
| Multipliez les numérateurs et multipliez les dénominateurs | Multipliez la première fraction par l'inverse de la seconde. |
| Addition de fractions | Soustraction de fractions |
| \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) | \(\dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\) |
| Additionnez les numérateurs et placez la somme au-dessus du dénominateur commun. | Soustrayez les numérateurs et placez la différence au-dessus du dénominateur commun. |
|
Pour multiplier ou diviser des fractions, aucun écran LCD n'est nécessaire. Pour ajouter ou soustraire des fractions, un écran LCD est nécessaire. |
|
Lorsque vous commencez un exercice, identifiez toujours l'opération, puis rappelez les méthodes nécessaires à cette opération.
Simplifier : ⓐ\(\dfrac{5x}{6}−\dfrac{3}{10}\) ⓑ\(\dfrac{5x}{6}·\dfrac{3}{10}\).
- Réponse
-
Demandez d'abord : « En quoi consiste l'opération ? » L'identification de l'opération déterminera si nous avons besoin d'un dénominateur commun. N'oubliez pas que nous avons besoin d'un dénominateur commun pour additionner ou soustraire, mais pas pour multiplier ou diviser.
ⓐ
\ (\ begin {array} {lc} \ text {Quelle est l'opération ? L'opération est la soustraction.} \ \ [6pt] \ text {Les fractions ont-elles un dénominateur commun ? Non.} & \ dfrac {5x} {6} − \ dfrac {3} {10} \ \ [6pt] \ text {Trouvez l'écran LCD de} 6 \ text {et} 10 & \ text {L'écran LCD fait 30.} \ \ [6pt] {\ begin {align*} 6 & =2·3 \ \ [6pt]
\ ; \ ; \ underline {\ ; \ ; \ \ ; \ ; \ ; \ ;} & \ underline {=2 · 5 \ ; \ ; \ ; \ ;} \ ;} \ ; \ [6 points]
\ text {LCD} & =2 · 3 · 5 \ \ [6] pt]
\ text {LCD} & =30 \ end {align*}} \ \ [6pt] \ \ \ \
\ text {Réécrivez chaque fraction en tant que fraction équivalente avec l'écran LCD.} & \ dfrac {5x·5} {6·5} − \ dfrac {3·3} {10·3} \ \ [6pt] \ text {} &
\ dfrac {25x} {30} − \ dfrac {9} {30} \ \ [6pt] \ [6pt]
\ text {Soustrayez les numérateurs et placez la différence} \ \ [6pt]
\ text {sur le point commun dénominateurs.} & \ dfrac {25x−9} {30} \ \ [6pt] \ \ \ \
\ text {Simplifiez, si possible. Il n'y a pas de facteurs communs.} \ \ [6pt]
\ text {La fraction est simplifiée.} \ end {tableau} \)ⓑ
\(\begin{array}{lc} \text{What is the operation? Multiplication.} & \dfrac{25x}{6}·\dfrac{3}{10} \\ \text{To multiply fractions,multiply the numerators} \\ \text{and multiply the denominators.} & \dfrac{25x·3}{6·10} \\ \text{Rewrite, showing common factors.} \\ \text{Remove common factors.} & \dfrac{\cancel{5} x · \cancel{3}}{2·\cancel{3}·2·\cancel{5}} \\ \text{Simplify.} & \dfrac{x}{4} \end{array}\)
Remarquez que nous avions besoin d'un écran LCD pour ajouter\(\dfrac{25x}{6}−\dfrac{3}{10}\), mais pas pour multiplier\(\dfrac{25x}{6}⋅\dfrac{3}{10}\).
Simplifier : ⓐ\(\dfrac{3a}{4}−\dfrac{8}{9}\) ⓑ\(\dfrac{3a}{4}·\dfrac{8}{9}\).
- Réponse
-
ⓐ\(\dfrac{27a−32}{36}\) ⓑ\(\dfrac{2a}{3}\)
Simplifier : ⓐ\(\dfrac{4k}{5}−\dfrac{1}{6}\) ⓑ\(\dfrac{4k}{5}⋅\dfrac{1}{6}\).
- Réponse
-
ⓐ\(\dfrac{24k−5}{30}\) ⓑ\(\dfrac{2k}{15}\)
Utiliser l'ordre des opérations pour simplifier les fractions
La barre de fraction d'une fraction fait office de symbole de regroupement. L'ordre des opérations nous indique ensuite de simplifier le numérateur puis le dénominateur. Ensuite, nous divisons.
- Simplifiez l'expression dans le numérateur. Simplifiez l'expression dans le dénominateur.
- Simplifiez la fraction.
Où va le signe négatif en une fraction ? Habituellement, le signe négatif se trouve devant la fraction, mais vous verrez parfois une fraction avec un numérateur négatif, ou parfois avec un dénominateur négatif. N'oubliez pas que les fractions représentent la division. Lorsque le numérateur et le dénominateur ont des signes différents, le quotient est négatif.
\[\dfrac{−1}{3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{negative}}{\text{positive}}=\text{negative}\]
\[\dfrac{1}{−3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{positive}}{\text{negative}}=\text{negative}\]
Pour tous les nombres positifs\(a\) et\(b\),
\[\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\]
Simplifiez :\(\dfrac{4(−3)+6(−2)}{−3(2)−2}\).
- Réponse
-
La barre de fraction agit comme un symbole de regroupement. Simplifiez donc complètement le numérateur et le dénominateur séparément.
\(\begin{array}{lc} \text{} & \dfrac{4(−3)+6(−2)}{−3(2)−2} \\[5pt] \text{Multiply.} & \dfrac{−12+(−12)}{−6−2} \\[5pt] \text{Simplify.} & \dfrac{−24}{−8} \\[5pt] \text{Divide.} & 3 \end{array}\)
Simplifiez :\(\dfrac{8(−2)+4(−3)}{−5(2)+3}\).
- Réponse
-
4
Simplifiez :\(\dfrac{7(−1)+9(−3)}{−5(3)−2}\).
- Réponse
-
2
Nous allons maintenant examiner les fractions complexes dont le numérateur ou le dénominateur contient une expression qui peut être simplifiée. Il faut donc d'abord simplifier complètement le numérateur et le dénominateur séparément en utilisant l'ordre des opérations. Ensuite, nous divisons le numérateur par le dénominateur, car la barre de fraction signifie division.
Simplifiez :\(\dfrac{\left(\frac{1}{2}\right)^2}{4+3^2}\).
- Réponse
-
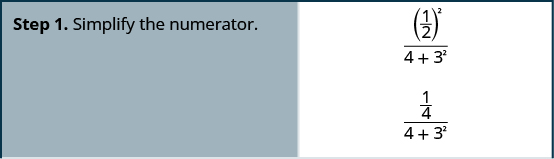


Simplifiez :\(\dfrac{\left(\frac{1}{3}\right)^2}{2^3+2}\).
- Réponse
-
\(\frac{1}{90}\)
Simplifiez :\(\dfrac{1+4^2}{\left(\frac{1}{4}\right)^2}\).
- Réponse
-
272
- Simplifiez le numérateur.
- Simplifiez le dénominateur.
- Divisez le numérateur par le dénominateur. Simplifiez si possible.
Simplifiez :\(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}}\).
- Réponse
-
Il peut être utile de placer le numérateur et le dénominateur entre parenthèses.
\(\begin{array}{lc}\text{} & \dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}} \\[6pt] \text{Simplify the numerator }(LCD=6)\text{ and } \\[6pt] \text{simplify the denominator }(LCD=12). & \dfrac{\left(\dfrac{3}{6}+\dfrac{4}{6}\right)}{\left(\dfrac{9}{12}−\dfrac{2}{12}\right)} \\[6pt] \text{Simplify.} & \left(\dfrac{7}{6}\right)\left(\dfrac{7}{12}\right) \\[6pt] \text{Divide the numerator by the denominator.} & \dfrac{7}{6}÷\dfrac{7}{12} \\[6pt] \text{Simplify.} & \dfrac{7}{6}⋅\dfrac{12}{7} \\[6pt] \text{Divide out common factors.} & \dfrac{\cancel{7}⋅\cancel{6}⋅2}{ \cancel{6}⋅\cancel{7}⋅1} \\[6pt] \text{Simplify.} & 2 \end{array}\)
Simplifiez :\( \dfrac{\dfrac{1}{3}+\dfrac{1}{2}}{ \dfrac{3}{4}−\dfrac{1}{3}}\).
- Réponse
-
2
Simplifiez :\(\dfrac{\dfrac{2}{3}−\dfrac{1}{2}}{ \dfrac{1}{4}+\dfrac{1}{3}}\).
- Réponse
-
\(\frac{2}{7}\)
Évaluer des expressions variables avec des fractions
Nous avons déjà évalué des expressions, mais nous pouvons maintenant évaluer des expressions avec des fractions. N'oubliez pas que pour évaluer une expression, nous substituons la valeur de la variable dans l'expression, puis nous simplifions.
Évaluez\(2x^2y\) quand\(x=\frac{1}{4}\) et\(y=−\frac{2}{3}\).
- Réponse
-
Substituez les valeurs dans l'expression.
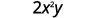
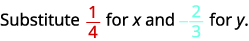
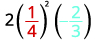
Simplifiez d'abord les exposants 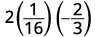
Multipliez ; divisez les facteurs communs. Notez que nous écrivons 16 sous la forme 2⋅2⋅42·2·4 pour faciliter la suppression des facteurs courants. 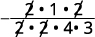
Simplifiez. 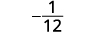
Évaluez\(3ab^2\) quand\(a=−\frac{2}{3}\) et\(b=−\frac{1}{2}\).
- Réponse
-
\(−\dfrac{1}{2}\)
Évaluez\(4c^3d\) quand\(c=−\frac{1}{2}\) et\(d=−\frac{4}{3}\).
- Réponse
-
\(\dfrac{2}{3}\)
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner avec les fractions.
- Additionner des fractions avec des dénominateurs différents
Concepts clés
- Si\(a\)\(b\), et\(c\) sont des nombres où\(b≠0,c≠0\), alors
\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\)et\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
- Comment simplifier une fraction.
- Réécrivez le numérateur et le dénominateur pour montrer les facteurs communs.
Au besoin, factorisez d'abord le numérateur et le dénominateur en nombres premiers. - Simplifiez l'utilisation de la propriété Fractions équivalentes en divisant les facteurs communs.
- Multipliez tous les facteurs restants.
- Réécrivez le numérateur et le dénominateur pour montrer les facteurs communs.
- Si\(a\),\(b\)\(c\), et\(d\) sont des nombres où\(b≠0\), et\(d≠0\), alors
\(\dfrac{a}{b}·\dfrac{c}{d}=\dfrac{ac}{bd}\)
Pour multiplier les fractions, multipliez les numérateurs et multipliez les dénominateurs.
- Si\(a\),\(b\)\(c\), et\(d\) sont des nombres où\(b≠0\)\(c≠0\), et\(d≠0\), alors
\(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)
Pour diviser des fractions, on multiplie la première fraction par l'inverse de la seconde.
- Si\(a\)\(b\), et\(c\) sont des nombres où\(c≠0\), alors
\(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)
Pour ajouter ou soustraire des fractions, ajoutez ou soustrayez les numérateurs et placez le résultat au-dessus du dénominateur commun.
- Comment ajouter ou soustraire des fractions.
- Ont-ils un dénominateur commun ?
- Oui, passez à l'étape 2.
- NON : réécrivez chaque fraction à l'aide de l'écran LCD (le plus petit dénominateur commun).
- Trouvez l'écran LCD.
- Changez chaque fraction en une fraction équivalente avec l'écran LCD comme dénominateur.
- Ajoutez ou soustrayez les fractions.
- Simplifiez, si possible.
- Ont-ils un dénominateur commun ?
- Comment simplifier une expression à l'aide d'une barre de fraction.
- Simplifiez l'expression dans le numérateur. Simplifiez l'expression dans le dénominateur.
- Simplifiez la fraction.
- Pour tous les nombres positifs\(a\) et\(b\),
\(\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\)
- Comment simplifier les fractions complexes.
- Simplifiez le numérateur.
- Simplifiez le dénominateur.
- Divisez le numérateur par le dénominateur. Simplifiez si possible.
Lexique
- fraction complexe
- Une fraction dont le numérateur ou le dénominateur est une fraction est appelée fraction complexe.
- dénominateur
- Dans une fraction, écrite\(\dfrac{a}{b}\)\(b≠0\), où le dénominateur\(b\) est le nombre de parties égales en lesquelles le tout a été divisé.
- fractions équivalentes
- Les fractions équivalentes sont des fractions qui ont la même valeur.
- fraction
- Une fraction s'écrit\(\dfrac{a}{b}\), où\(b≠0\), et a est le numérateur et\(b\) le dénominateur. Une fraction représente des parties d'un tout.
- plus petit dénominateur commun
- Le plus petit dénominateur commun (LCD) de deux fractions est le plus petit multiple commun (LCM) de leurs dénominateurs.
- numérateur
- Dans une fraction, écrite\(\dfrac{a}{b}\)\(b≠0\), où le numérateur a indique le nombre de parties incluses.
- réciproque
- L'inverse d'une fraction est trouvé en inversant la fraction, en plaçant le numérateur dans le dénominateur et le dénominateur dans le numérateur.


