1.3E : Exercices

Last updated
Save as PDF

Page ID: 194235

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La pratique rend la perfection

Simplifier les expressions avec une valeur

Dans les exercices suivants, saisissez$<,>,$ ou$=$ pour chacune des paires de nombres suivantes.

1. ⓐ$|−7| \text{ ___ }−|−7|$

ⓑ$6 \text{ ___ }−|−6|$

ⓒ$|−11|\text{ ___ }−11$

ⓓ$−(−13)\text{ ___ }−|−13|$

Réponse: ⓐ$>$ ⓑ$>$ ⓒ$>$ ⓓ$>$

2. ⓐ$−|−9| \text{ ___ } |−9|$

ⓑ$−8 \text{ ___ } |−8| $

ⓒ$|−1| \text{ ___ } −1 $

ⓓ$−(−14) \text{ ___ } −|−14|$

3. ⓐ$−|2| \text{ ___ }−|−2|$

ⓑ$−12 \text{ ___ }−|−12|$

ⓒ$|−3| \text{ ___ }−3$

ⓓ$|−19| \text{ ___ }−(−19) $

Réponse: ⓐ$=$ ⓑ$=$ ⓒ$>$ ⓓ$=$

4. ⓐ$−|−4| \text{ ___ } −|4| $

ⓑ$5 \text{ ___ } −|−5| $

ⓒ$ −|−10| \text{ ___ } −10 $

ⓓ$−|−0| \text{ ___ } −(−0) $

Dans les exercices suivants, simplifiez.

5. $|15−7|−|14−6|$

Réponse: 0

6. $|17−8|−|13−4|$

7. $18−|2(8−3)|$

Réponse: 8

8. $15−|3(8−5)|$

9. $18−|12−4(4−1)+3|$

Réponse: 15

10. $27−|19+4(3−1)−7|$

11. $10−3|9−3(3−1)|$

Réponse: 1

12. $13−2|11−2(5−2)|$

Ajouter et soustraire des entiers

Dans les exercices suivants, simplifiez chaque expression.

13. ⓐ$−7+(−4)$

ⓑ$−7+4$

ⓒ$7+(−4).$

Réponse: ⓐ$−11$ ⓑ$−3$ ⓒ$3$

14. ⓐ$−5+(−9)$

ⓑ$−5+9$

ⓒ$5+(−9)$

15. $48+(−16)$

Réponse: 32

16. $34+(−19)$

17. $−14+(−12)+4$

Réponse: $-22$

18. $−17+(−18)+6$

19. $19+2(−3+8)$

Réponse: $29$

20. $24+3(−5+9)$

21. ⓐ$13−7$

ⓑ$−13−(−7)$

ⓒ$−13−7$

ⓓ$13−(−7)$

Réponse: ⓐ 6 ⓑ −6 ⓒ −20 ⓓ 20

22. ⓐ$15−8$

ⓑ$−15−(−8)$

ⓒ$−15−8$

ⓓ$15−(−8)$

23. $−17−42$

Réponse: $-59$

24. $−58−(−67)$

25. $−14−(−27)+9$

Réponse: 22

26. $64+(−17)−9$

27. ⓐ$44−28$ ⓑ$44+(−28)$

Réponse: ⓐ 16 ⓑ 16

28. ⓐ$35−16$ ⓑ$35+(−16)$

29. ⓐ$27−(−18)$ ⓑ$27+18$

Réponse: ⓐ 45 ⓑ 45

30. ⓐ$46−(−37)$ ⓑ$46+37$

31. $(2−7)−(3−8)$

Réponse: 0

32. $(1−8)−(2−9)$

33. $−(6−8)−(2−4)$

Réponse: 4

34. $−(4−5)−(7−8)$

35. $25−[10−(3−12)]$

Réponse: 6

36. $32−[5−(15−20)]$

Multipliez et divisez des entiers

Dans les exercices suivants, multipliez ou divisez.

37. ⓐ$−4⋅8$

ⓑ$13(−5)$

ⓒ$−24÷6$

ⓓ$−52÷(−4)$

Réponse: ⓐ$−32$ ⓑ$−65$ ⓒ$−4$ ⓓ$13$

38. ⓐ$−3⋅9$

ⓑ$9(−7)$

ⓒ$35÷(−7)$

ⓓ$−84÷(−6)$

39. ⓐ$−28÷7$

ⓑ$−180÷15$

ⓒ$3(−13)$

ⓓ$−1(−14)$

Réponse: ⓐ$−4$ ⓑ$−12$ ⓒ$−39$ ⓓ$14$

40. ⓐ$−36÷4$

ⓑ$−192÷12$

ⓒ$9(−7)$

ⓓ$−1(−19)$

Simplifier et évaluer des expressions avec des nombres entiers

Dans les exercices suivants, simplifiez chaque expression.

41. ⓐ$(−2)^6$ ⓑ$−2^6$

Réponse: ⓐ$64$ ⓑ$−64$

42. ⓐ$(−3)^5$ ⓑ$−3^5$

43. $5(−6)+7(−2)−3$

Réponse: $−47$

44. $8(−4)+5(−4)−6$

45. $−3(−5)(6)$

Réponse: $90$

46. $−4(−6)(3)$

47. $(8−11)(9−12)$

Réponse: $9$

48. $(6−11)(8−13)$

49. $26−3(2−7)$

Réponse: $41$

50. $23−2(4−6)$

51. $65÷(−5)+(−28)÷(−7)$

Réponse: $-9$

52. $52÷(−4)+(−32)÷(−8)$

53. $9−2[3−8(−2)]$

Réponse: $-29$

54. $11−3[7−4(−2)]$

55. $8−|2−4(4−1)+3|$

Réponse: $1$

56. $7−|5−3(4−1)−6|$

57. $9−3|2(2−6)−(3−7)|$

Réponse: $-3$

58. $5−2|2(1−4)−(2−5)|$

59. $(−3)^2−24÷(8−2)$

Réponse: $5$

60. $(−4)^2−32÷(12−4)$

Dans les exercices suivants, évaluez chaque expression.

61. $y+(−14)$quand ⓐ$y=−33$ ⓑ$y=30$

Réponse: ⓐ$−47$ ⓑ$16$

62. $x+(−21)$quand ⓐ$x=−27$ ⓑ$x=44$

63. $(x+y)^2$quand$x=−3$ et$y=14$

Réponse: $121$

64. $(y+z)^2$quand$y=−3$ et$z=15$

65. $9a−2b−8$quand$a=−6$ et$b=−3$

Réponse: $-56$

66. $7m−4n−2$quand$m=−4$ et$n=−9$

67. $3x^2−4xy+2y^2$quand$x=−2$ et$y=−3$

Réponse: $6$

68. $4x^2−xy+3y^2$quand$x=−3$ et$y=−2$

Traduire des phrases anglaises en expressions algébriques

Dans les exercices suivants, traduisez en une expression algébrique et simplifiez si possible.

69. la somme de 3 et −15, augmentée de 7

Réponse: $(3+(−15))+7;−5$

70. la somme de$−8$ et$−9$, augmentée de$23$

71. ⓐ la différence entre$10$ et$−18$

ⓑ soustraire$11$ de$−25$

Réponse

ⓐ$10−(−18);28$

ⓑ$−25−11;−36$

72. ⓐ la différence entre$−5$ et$−30$

ⓑ soustraire$−6$ de$−13$

73. le quotient$−6$ et la somme de$a$ et$b$

Réponse: $\dfrac{−6}{a+b}$

74. le produit$−13$ et la$c$ différence entre$d$

Utiliser des nombres entiers dans les applications

Dans les exercices suivants, résolvez.

75. Température Le 15 janvier, la température maximale à Anaheim, en Californie, était$84°$. Le même jour, la température élevée à Embarrass, dans le Minnesota, était$−12°$. Quelle était la différence entre la température à Anaheim et la température à Embarrass ?

Réponse: $96^\circ$

76. Température Le 21 janvier, la température maximale à Palm Springs, en Californie, était$89°$, et la température élevée à Whitefield, dans le New Hampshire, était$−31°$. Quelle était la différence entre la température à Palm Springs et la température à Whitefield ?

77. Football Lors de la première manche, les Chargers avaient le ballon sur leur ligne de 25 mètres. Lors des trois descentes suivantes, ils ont perdu 6 mètres, gagné 10 mètres et perdu 8 mètres. Quelle était la ligne de triage à la fin de la quatrième descente ?

Réponse: 21

78. Football Au premier but, les Steelers avaient le ballon sur leur ligne de 30 mètres. Lors des trois descentes suivantes, ils ont gagné 9 yards, perdu 14 yards et perdu 2 yards. Quelle était la ligne de triage à la fin de la quatrième descente ?

79. Compte courant Mayra a 124$ sur son compte courant. Elle fait un chèque de 152$. Quel est le nouveau solde de son compte courant ?

Réponse: $−\$ 28$

80. Compte courant Reymonte a un solde$−$49$ de sur son compte courant. Il dépose 281$ sur le compte. Qu'est-ce que le nouvel équilibre ?

Exercices d'écriture

81. Expliquez pourquoi la somme de −8 et de 2 est négative, alors que la somme de 8 et −2 est positive.

Réponse: Les réponses peuvent varier.

82. Donnez un exemple tiré de votre expérience de vie où vous avez ajouté deux nombres négatifs.

83. Dans vos propres termes, énoncez les règles de multiplication et de division des nombres entiers.

Réponse: Les réponses peuvent varier.

84. Pourquoi$−4^3=(−4)^3$ ?

Auto-vérification

ⓐ Après avoir terminé les exemples, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

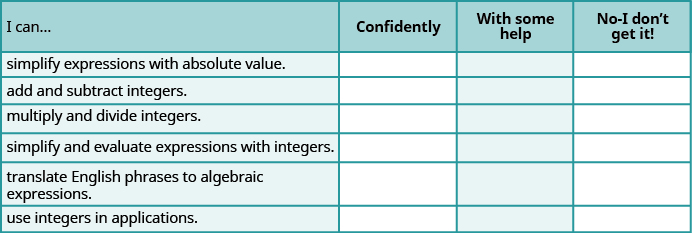
$Ce tableau comporte 4 colonnes, 6 lignes et une ligne d'en-tête. La ligne d'en-tête étiquette chaque colonne que je peux, en toute confiance, avec de l'aide et non, je ne comprends pas. La première colonne contient les instructions suivantes : simplifier les expressions avec une valeur absolue, ajouter et soustraire des entiers, multiplier et diviser des entiers, simplifier et évaluer des expressions avec des entiers, traduire des phrases anglaises en expressions algébriques, utiliser des entiers dans les applications. Les colonnes restantes sont vides.$

ⓑ Après avoir examiné cette liste de contrôle, que ferez-vous pour atteindre tous les objectifs en toute confiance ?