1.3 : Entiers
- Page ID
- 194227
À la fin de cette section, vous serez en mesure de :
- Simplifier les expressions avec une valeur
- Ajouter et soustraire des entiers
- Multipliez et divisez des entiers
- Simplifier les expressions avec des entiers
- Evaluer des expressions variables avec des nombres entiers
- Traduisez des phrases en expressions avec des nombres entiers
- Utiliser des nombres entiers dans les applications
Une introduction plus complète aux sujets abordés dans cette section se trouve dans le chapitre sur l'algèbre élémentaire, Fondations.
Simplifier les expressions avec une valeur
Un nombre négatif est un nombre inférieur à 0. Les nombres négatifs se situent à gauche de zéro sur la ligne numérique (Figure\(\PageIndex{1}\)).
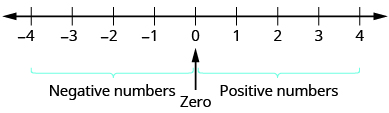
Chiffre\(\PageIndex{1}\). La ligne numérique indique l'emplacement des nombres positifs et négatifs.
Vous avez peut-être remarqué que, sur la ligne numérique, les nombres négatifs sont une image miroir des nombres positifs, avec zéro au milieu. Comme les nombres\(2\) et\(−2\) sont à la même distance de zéro, chacun est appelé le contraire de l'autre. Le contraire de l'\(2\)est\(−2\) et le contraire de l'\(−2\)est\(2\).
L'opposé d'un nombre est le nombre qui se trouve à la même distance de zéro sur la ligne numérique mais du côté opposé à zéro.
La figure\(\PageIndex{2}\) illustre la définition.

Chiffre\(\PageIndex{2}\). L'opposé de 3 est\(−3\).
\[\begin{align} & -a \text{ means the opposite of the number }a \\ & \text{The notation} -a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
Nous avons vu que les nombres tels que 3 et −3 sont opposés car ils se trouvent à la même distance de 0 sur la droite numérique. Ce sont deux unités de trois unités à partir de 0. La distance entre 0 et n'importe quel nombre sur la ligne numérique est appelée valeur absolue de ce nombre.
La valeur absolue d'un nombre est sa distance par rapport à 0 sur la ligne numérique.
La valeur absolue d'un nombre\(n\) est écrite au fur\(|n|\) et à mesure\(|n|≥0\) de tous les nombres.
Les valeurs absolues sont toujours supérieures ou égales à zéro.
Par exemple,
\[\begin{align} & -5 \text{ is } 5 \text{ units away from 0, so } |-5|=5. \\ & 5 \text{ is }5\text{ units away from 0, so }|5|=5. \end{align}\]
La figure\(\PageIndex{3}\) illustre cette idée.
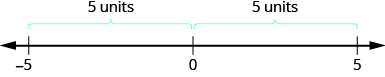
La valeur absolue d'un nombre n'est jamais négative car la distance ne peut pas être négative. Le seul nombre dont la valeur absolue est égale à zéro est le nombre zéro lui-même, car la distance entre 0 et 0 sur la ligne numérique est égale à zéro unité.
Dans l'exemple suivant, nous allons classer les expressions avec des valeurs absolues.
Renseignez\(<,\,>,\) ou\(=\) pour chacune des paires de chiffres suivantes :
- \(\mathrm{|−5|}\_\_\mathrm{−|−5|}\_\_\mathrm{−|5|}\)
- \(\text{8__−|−8|}\)
- \(\text{−9__−|−9|}\)
- (\ text {− (−16) __|−16|} \).
- Réponse
-
un.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {|−5| \\ 5 \\ 5 \\ |−5|} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−5| \\ −5 \\ −5 \\ −|−5|} \end{array}\)
b.
\(\begin{array}{llcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {8 \\ 8 \\ 8 \\ 8} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−8| \\ −8 \\ −8 \\ −|−8|} \end{array}\)
c.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−9 \\ −9 \\ −9 \\ −9} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−9| \\ −9 \\ −9 \\ −|−9|} \end{array}\)
d.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−(−16) \\ 16 \\ 16 \\ −(−16)} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−16| \\ 16 \\ 16 \\ |−16|} \end{array}\)
Renseignez\(<,\,>,\) ou\(=\) pour chacune des paires de chiffres suivantes :
ⓐ\(−9 \_\_−|−9|\) ⓑ\(2 \_\_−|−2|\) ⓒ\(−8 \_\_|−8|\) ⓓ\(−(−9) \_\_|−9|.\)
- Réponse
-
ⓐ\(>\) ⓑ\(>\) ⓒ\(<\)
ⓓ\(=\)
Renseignez\(<,>,\) ou\(=\) pour chacune des paires de chiffres suivantes :
- \(7 \_\_ −|−7|\)
- \(−(−10) \_ \_|−10|\)
- \(|−4| \_\_ −|−4|\)
- \(−1 \_\_ |−1|.\)
- Réponse
-
ⓐ\(>\) ⓑ\(=\) ⓒ\(>\)
ⓓ\(<\)
Nous ajoutons maintenant des barres de valeurs absolues à notre liste de symboles de regroupement. Lorsque nous utilisons l'ordre des opérations, nous simplifions d'abord autant que possible l'intérieur des barres de valeurs absolues, puis nous prenons la valeur absolue du nombre obtenu.
\[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
Dans l'exemple suivant, nous simplifierons d'abord les expressions à l'intérieur des barres de valeurs absolues, comme nous le faisons pour les parenthèses.
Simplifiez :\(\mathrm{24−|19−3(6−2)|}\).
- Réponse
-
\(\begin{array}{lc} \text{} & 24−|19−3(6−2)| \\ \text{Work inside parentheses first:} & \text{} \\ \text{subtract 2 from 6.} & 24−|19−3(4)| \\ \text{Multiply 3(4).} & 24−|19−12| \\ \text{Subtract inside the absolute value bars.} & 24−|7| \\ \text{Take the absolute value.} & 24−7 \\ \text{Subtract.} & 17 \end{array}\)
Simplifiez :\(19−|11−4(3−1)|\).
- Réponse
-
16
Simplifiez :\(9−|8−4(7−5)|\).
- Réponse
-
9
Ajouter et soustraire des entiers
Jusqu'à présent, dans nos exemples, nous n'avons utilisé que les nombres de comptage et les nombres entiers.
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3… \\ \text{Whole numbers} 0,1,2,3…. \end{array}\]
Notre travail avec les contraires nous permet de définir les nombres entiers. Les nombres entiers et leurs contraires sont appelés entiers. Les entiers sont des nombres\(…−3,−2,−1,0,1,2,3…\)
Les nombres entiers et leurs contraires sont appelés entiers.
Les entiers sont des nombres
\[…-3,-2,-1,0,1,2,3…,\]
La plupart des étudiants sont à l'aise avec les faits d'addition et de soustraction pour les nombres positifs. Mais faire des additions ou des soustractions avec des nombres positifs et négatifs peut s'avérer plus difficile.
Nous utiliserons deux compteurs de couleurs pour modéliser l'addition et la soustraction de négatifs afin que vous puissiez visualiser les procédures au lieu de mémoriser les règles.
Nous laissons une couleur (le bleu) représenter le positif. L'autre couleur (rouge) représentera les négatifs.

Si nous avons un compteur positif et un compteur négatif, la valeur de la paire est nulle. Ils forment une paire neutre. La valeur de cette paire neutre est nulle.
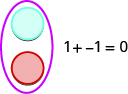
Nous utiliserons les compteurs pour montrer comment ajouter :
\[5+3 \; \; \; \; \; \; −5+(−3) \; \; \; \; \; \; −5+3 \; \; \; \; \; \; \; 5+(−3)\]
Le premier exemple\(5+3,\) ajoute 5 points positifs et 3 points positifs, tous deux positifs.
Le deuxième exemple\(−5+(−3),\) ajoute 5 négatifs et 3 négatifs, les deux négatifs.
Lorsque les signes sont les mêmes, les compteurs sont tous de la même couleur, nous les ajoutons donc. Dans chaque cas, nous obtenons 8, soit 8 points positifs, soit 8 négatifs.

Que se passe-t-il donc lorsque les signes sont différents ? Ajoutons\(−5+3\) et\(5+(−3)\).
Lorsque nous utilisons des compteurs pour modéliser l'addition d'entiers positifs et négatifs, il est facile de voir s'il y a plus de compteurs positifs ou négatifs. Nous savons donc si la somme sera positive ou négative.
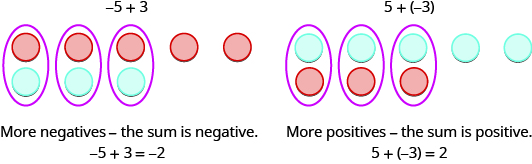
Ajoutez : ⓐ\(−1+(−4)\) ⓑ\(−1+5\) ⓒ\(1+(−5)\).
- Réponse
-
ⓐ
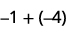

1 négatif plus 4 négatifs, soit 5 négatifs 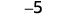
ⓑ
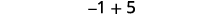

Il y a plus de points positifs, donc la somme est positive. 
ⓒ
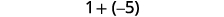

Il y a plus de points négatifs, donc la somme est négative. 
Ajoutez : ⓐ\(−2+(−4)\) ⓑ\(−2+4\) ⓒ\(2+(−4)\).
- Réponse
-
ⓐ\(−6\) ⓑ\(2\) ⓒ\(−2\)
Ajoutez : ⓐ\(−2+(−5)\) ⓑ\(−2+5\) ⓒ\(2+(−5)\).
- Réponse
-
ⓐ\(−7\) ⓑ\(3\) ⓒ\(−3\)
Nous continuerons à utiliser des compteurs pour modéliser la soustraction. Peut-être que quand tu étais plus jeune, tu\(“5−3”\) lisais « 5 plats à emporter 3 ». Lorsque vous utilisez des compteurs, vous pouvez penser à la soustraction de la même manière !
Nous utiliserons les compteurs pour montrer comment soustraire :
\[5−3 \; \; \; \; \; \; −5−(−3) \; \; \; \; \; \; −5−3 \; \; \; \; \; \; 5−(−3) \]
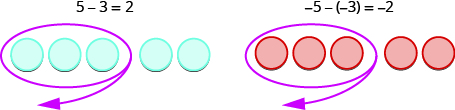
Dans le premier exemple\(5−3\), nous soustrayons 3 points positifs de 5 positifs et nous obtenons 2 positifs.
Dans le deuxième exemple,\(−5−(−3),\) nous soustrayons 3 négatifs de 5 négatifs et nous obtenons 2 négatifs.
Chaque exemple utilisait des compteurs d'une seule couleur, et le modèle de soustraction « à emporter » était facile à appliquer.
Que se passe-t-il lorsque nous devons soustraire un nombre positif et un nombre négatif ? Nous devrons utiliser à la fois des compteurs bleus et rouges ainsi que des paires neutres. Si nous n'avons pas le nombre de pions nécessaires à emporter, nous ajoutons des paires neutres. L'ajout d'une paire neutre ne modifie pas la valeur. C'est comme remplacer les pièces par des pièces de cinq cents : la valeur est la même, mais elle a une apparence différente.
Regardons\(−5−3\) et\(5−(−3)\).
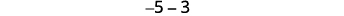 |
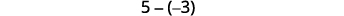 |
|
| Modélisez le premier chiffre. |  |
 |
| Nous ajoutons maintenant les paires neutres nécessaires. |  |
 |
| Nous supprimons le nombre de compteurs modélisés par le deuxième nombre. | 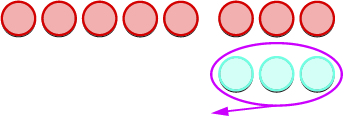 |
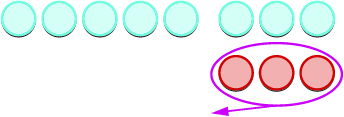 |
| Comptez ce qui reste. |  |
 |
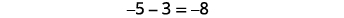 |
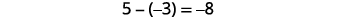 |
|
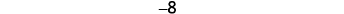 |
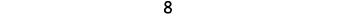 |
Soustraire : ⓐ\(3−1\) ⓑ\(−3−(−1)\) ⓒ\(−3−1\) ⓓ\(3−(−1)\).
- Réponse
-
ⓐ
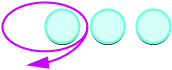
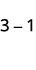
Prenez 1 positif parmi 3 positifs et obtenez 2 positifs. 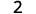
ⓑ

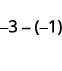
Prenez 1 positif parmi 3 négatifs et obtenez 2 négatifs. 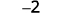
ⓒ

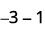
Prenez 1 résultat positif de la paire neutre ajoutée. 
ⓓ

Prenez 1 négatif de la paire neutre ajoutée. 

Soustraire : ⓐ\(6−4\) ⓑ\(−6−(−4)\) ⓒ\(−6−4\) ⓓ\(6−(−4)\).
- Réponse
-
ⓐ\(2\) ⓑ\(−2\) ⓒ\(−10\) ⓓ\(10\)
Soustraire : ⓐ\(7−4\) ⓑ\(−7−(−4)\) ⓒ\(−7−4\) ⓓ\(7−(−4)\).
- Réponse
-
ⓐ\(3\) ⓑ\(−3\) ⓒ\(−11\) ⓓ\(11\)
Avez-vous remarqué qu'il est possible de soustraire des nombres signés en ajoutant le contraire ? Dans le dernier exemple,\(−3−1\) est identique à\(−3+(−1)\) et\(3−(−1)\) est identique à\(3+1\). Vous verrez souvent cette idée, la propriété de soustraction, écrite comme suit :
\[a−b=a+(−b)\]
Soustraire un nombre revient à ajouter son opposé.
Simplifiez : ⓐ\(13−8\) et\(13+(−8)\) ⓑ\(−17−9\) et\(−17+(−9)\) ⓒ\(9−(−15)\) et\(9+15\) ⓓ\(−7−(−4)\) et\(−7+4\).
- Réponse
-
ⓐ
\(\begin{array}{lccc} \text{} & 13−8 & \text{and} & 13+(−8) \\ \text{Subtract.} & 5 & \text{} & 5 \end{array}\)ⓑ
\(\begin{array}{lccc} \text{} & −17−9 & \text{and} & −17+(−9) \\ \text{Subtract.} & −26 & \text{} & −26 \end{array}\)
ⓒ
\(\begin{array}{lccc} \text{} & 9−(−15) & \text{and} & 9+15 \\ \text{Subtract.} & 24 & \text{} & 24 \end{array}\)
ⓓ
\(\begin{array}{lccc} \text{} & −7−(−4) & \text{and} & −7+4 \\ \text{Subtract.} & −3 & \text{} & −3 \end{array}\)
Simplifiez : ⓐ\(21−13\) et\(21+(−13)\) ⓑ\(−11−7\) et\(−11+(−7)\) ⓒ\(6−(−13)\) et\(6+13\) ⓓ\(−5−(−1)\) et\(−5+1\).
- Réponse
-
ⓐ\(8,8\) ⓑ\(−18,−18\)
ⓒ\(19,19\) ⓓ\(−4,−4\)
Simplifiez : ⓐ\(15−7\) et\(15+(−7)\) ⓑ\(−14−8\) et\(−14+(−8)\) ⓒ\(4−(−19)\) et\(4+19\) ⓓ\(−4−(−7)\) et\(−4+7\).
- Réponse
-
ⓐ\(8,8\) ⓑ\(−22,−22\)
ⓒ\(23,23\) ⓓ\(3,3\)
Que se passe-t-il lorsqu'il y a plus de trois entiers ? Nous utilisons simplement l'ordre des opérations comme d'habitude.
Simplifiez :\(7−(−4−3)−9.\)
- Réponse
-
\(\begin{array}{lc} \text{} & 7−(−4−3)−9 \\ \text{Simplify inside the parentheses first.} & 7−(−7)−9 \\ \text{Subtract left to right.} & 14−9 \\ \text{Subtract.} & 5 \end{array}\)
Simplifiez :\(8−(−3−1)−9.\)
- Réponse
-
3
Simplifiez :\(12−(−9−6)−14.\)
- Réponse
-
13
Multipliez et divisez des entiers
Comme la multiplication est un raccourci mathématique désignant les additions répétées, notre modèle peut facilement être appliqué pour montrer la multiplication d'entiers. Examinons ce modèle concret pour voir quels modèles nous remarquons. Nous utiliserons les mêmes exemples que ceux que nous avons utilisés pour l'addition et la soustraction. Ici, nous utilisons le modèle uniquement pour nous aider à découvrir le modèle.
Nous nous souvenons que a⋅ba·b signifie ajouter a, b fois.
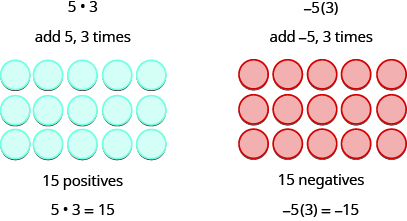
Les deux exemples suivants sont plus intéressants. Que signifie multiplier 5 par −3 ? Cela signifie soustraire 5,3 fois. Considérer la soustraction comme « à emporter », cela signifie en retirer 5 ou 3 fois. Mais il n'y a rien à retirer, nous commençons donc par ajouter des paires neutres sur l'espace de travail.
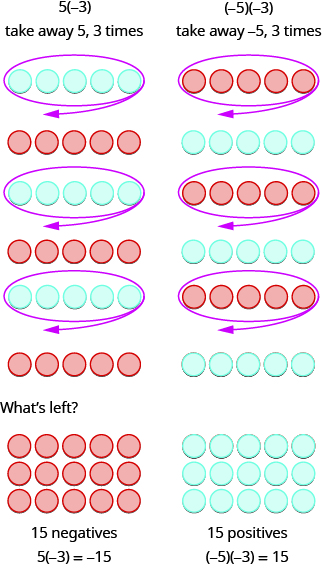
En résumé :
\[\begin{array}{ll} 5·3=15 & −5(3)=−15 \\ 5(−3)=−15 & (−5)(−3)=15 \end{array}\]
Notez que pour la multiplication de deux nombres signés, lorsque le
\[ \text{signs are the } \textbf{same} \text{, the product is } \textbf{positive.} \\ \text{signs are } \textbf{different} \text{, the product is } \textbf{negative.} \]
Qu'en est-il de la division ? La division est l'opération inverse de la multiplication. Donc,\(15÷3=5\) parce que\(15·3=15\). En d'autres termes, cette expression indique que 15 peuvent être divisés en 3 groupes de 5 chacun parce que l'ajout de cinq trois fois donne 15. Si vous regardez quelques exemples de multiplication d'entiers, vous pouvez trouver les règles de division des entiers.
\[\begin{array}{lclrccl} 5·3=15 & \text{so} & 15÷3=5 & \text{ } −5(3)=−15 & \text{so} & −15÷3=−5 \\ (−5)(−3)=15 & \text{so} & 15÷(−3)=−5 & \text{ } 5(−3)=−15 & \text{so} & −15÷(−3)=5 \end{array}\]
La division suit les mêmes règles que la multiplication en ce qui concerne les signes.
Pour la multiplication et la division de deux nombres signés :
| Mêmes signes | Résultat |
|---|---|
| • Deux points positifs | positif |
| • Deux points négatifs | positif |
Si les signes sont identiques, le résultat est positif.
| Différents signes | Résultat |
|---|---|
| • Positif et négatif | NÉGATIF |
| • Négatif et positif | NÉGATIF |
Si les signes sont différents, le résultat est négatif.
Multipliez ou divisez : ⓐ\(−100÷(−4)\) ⓑ\(7⋅6\) ⓒ\(4(−8)\) ⓓ\(−27÷3.\)
- Réponse
-
ⓐ
\(\begin{array}{lc} \text{} & −100÷(−4) \\ \text{Divide, with signs that are} \\ \text{the same the quotient is positive.} & 25 \end{array}\)
ⓑ
\(\begin{array} {lc} \text{} & 7·6 \\ \text{Multiply, with same signs.} & 42 \end{array}\)
ⓒ
\(\begin{array} {lc} \text{} & 4(−8) \\ \text{Multiply, with different signs.} & −32 \end{array}\)
ⓓ
\(\begin{array}{lc} \text{} & −27÷3 \\ \text{Divide, with different signs,} \\ \text{the quotient is negative.} & −9 \end{array}\)
Multipliez ou divisez : ⓐ\(−115÷(−5)\) ⓑ\(5⋅12\) ⓒ\(9(−7)\) ⓓ\(−63÷7.\)
- Réponse
-
ⓐ 23 ⓑ 60 ⓒ −63 ⓓ −9
Multipliez ou divisez : ⓐ\(−117÷(−3)\) ⓑ\(3⋅13\) ⓒ\(7(−4)\) ⓓ\(−42÷6\).
- Réponse
-
ⓐ 39 ⓑ 39 ⓒ −28 ⓓ −7
Lorsque nous multiplions un nombre par 1, le résultat est le même nombre. Chaque fois qu'on multiplie un nombre par −1, on obtient son contraire !
\[−1a=−a\]
Multiplier un nombre par\(−1\) donne son contraire.
Simplifier les expressions avec des entiers
Que se passe-t-il lorsqu'il y a plus de deux nombres dans une expression ? L'ordre des opérations s'applique toujours lorsque des négatifs sont inclus. Tu te souviens, excusez ma chère tante Sally ?
Essayons quelques exemples. Nous allons simplifier les expressions qui utilisent les quatre opérations avec des nombres entiers : addition, soustraction, multiplication et division. N'oubliez pas de suivre l'ordre des opérations.
Simplifier : ⓐ\((−2)^4\) ⓑ\(−2^4\).
- Réponse
-
Remarquez la différence entre les parties (a) et (b). Dans la partie (a), l'exposant signifie élever ce qui est entre parenthèses, le −2 à la 4e puissance. Dans la partie (b), l'exposant signifie élever uniquement la 2 à la 4e puissance, puis prendre l'inverse.
ⓐ
\(\begin{array}{lc} \text{} & (−2)^4 \\ \text{Write in expanded form.} & (−2)(−2)(−2)(−2) \\ \text{Multiply.} & 4(−2)(−2) \\ \text{Multiply.} & −8(−2) \\ \text{Multiply.} & 16 \end{array}\)ⓑ
\(\begin{array}{lc} \text{} & −2^4 \\ \text{Write in expanded form.} & −(2·2·2·2) \\ \text{We are asked to find} & \text{} \\ \text{the opposite of }24. & \text{} \\ \text{Multiply.} & −(4·2·2) \\ \text{Multiply.} & −(8·2) \\ \text{Multiply.} & −16 \end{array}\)
Simplifier : ⓐ\((−3)^4\) ⓑ\(−3^4\).
- Réponse
-
ⓐ 81 ⓑ −81
Simplifier : ⓐ\((−7)^2\) ⓑ\(−7^2\).
- Réponse
-
ⓐ 49 ⓑ −49
Le dernier exemple nous a montré la différence entre\((−2)^4\) et\(−2^4\). Cette distinction est importante pour éviter de futures erreurs. L'exemple suivant nous rappelle de multiplier et de diviser dans l'ordre de gauche à droite.
Simplifier : ⓐ\(8(−9)÷(−2)^3\) ⓑ\(−30÷2+(−3)(−7)\).
- Réponse
-
ⓐ
\(\begin{array}{lc} \text{} & 8(−9)÷(−2)^3 \\ \text{Exponents first.} & 8(−9)÷(−8) \\ \text{Multiply.} & −72÷(−8) \\ \text{Divide.} & 9 \end{array}\)
ⓑ
\(\begin{array}{lc} \text{} & −30÷2+(−3)(−7) \\ \text{Multiply and divide} \\ \text{left to right, so divide first.} & −15+(−3)(−7) \\ \text{Multiply.} & −15+21 \\ \text{Add.} & 6 \end{array}\)
Simplifier : ⓐ\(12(−9)÷(−3)^3\) ⓑ\(−27÷3+(−5)(−6).\)
- Réponse
-
ⓐ 4 ⓑ 21
Simplifier : ⓐ\(18(−4)÷(−2)^3\) ⓑ\(−32÷4+(−2)(−7).\)
- Réponse
-
ⓐ 9 ⓑ 6
Evaluer des expressions variables avec des entiers
N'oubliez pas que pour évaluer une expression, vous devez substituer un nombre à la variable de l'expression. Nous pouvons maintenant utiliser des nombres négatifs aussi bien que des nombres positifs.
Évaluez\(4x^2−2xy+3y^2\) quand\(x=2,y=−1\).
- Réponse
-
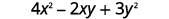
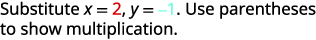
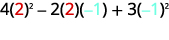
Simplifiez les exposants. 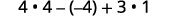
Multipliez. 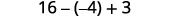
Soustraire. 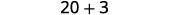
Ajoutez. 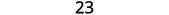
Évaluez :\(3x^2−2xy+6y^2\) quand\(x=1,y=−2\).
- Réponse
-
31
Évaluez :\(4x^2−xy+5y^2\) quand\(x=−2,y=3\).
- Réponse
-
67
Traduisez des phrases en expressions avec des nombres entiers
Nos travaux antérieurs sur la traduction de l'anglais en algèbre s'appliquent également aux phrases qui incluent à la fois des nombres positifs et négatifs.
Traduire et simplifier : somme de 8 et −12, augmentée de 3.
- Réponse
-
\(\begin{array}{lc} \text{} & \text{the } \textbf{sum } \underline{\text{of}} \; –8 \; \underline{\text{and}} −12 \text{ increased by } 3 \\ \text{Translate.} & [8+(−12)]+3 \\ \text{Simplify. Be careful not to confuse the} \; \; \; \; \; \; \; \; \; \; & (−4)+3 \\ \text{brackets with an absolute value sign.} \\ \text{Add.} & −1 \end{array}\)
Traduisez et simplifiez la somme de 9 et −16, augmentée de 4.
- Réponse
-
\((9+(−16))+4;−3\)
Traduisez et simplifiez la somme de −8 et −12, augmentée de 7.
- Réponse
-
\((−8+(−12))+7;−13\)
Utiliser des nombres entiers dans les applications
Nous allons présenter un plan pour résoudre les demandes. Il est difficile de trouver quelque chose si l'on ne sait pas ce que l'on cherche ou comment l'appeler ! Ainsi, lorsque nous résolvons une application, nous devons d'abord déterminer ce que le problème nous demande de trouver. Ensuite, nous allons écrire une phrase qui donne les informations nécessaires pour le trouver. Nous allons traduire la phrase en expression, puis simplifier l'expression pour obtenir la réponse. Enfin, nous résumons la réponse en une phrase pour nous assurer qu'elle a du sens.
La température à Kendallville, dans l'Indiana, un matin était de 11 degrés. En milieu d'après-midi, la température était tombée à −9−9 degrés. Quelle était la différence entre les températures du matin et de l'après-midi ?
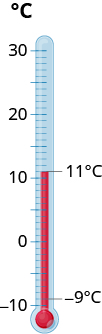
- Réponse
-






Un matin, la température à Anchorage, en Alaska, était de 15 degrés. En milieu d'après-midi, la température était tombée à 30 degrés en dessous de zéro. Quelle était la différence entre les températures du matin et de l'après-midi ?
- Réponse
-
La différence de température était de 45 degrés Fahrenheit.
La température à Denver était de −6 degrés à l'heure du déjeuner. Au coucher du soleil, la température était tombée à −15 degrés. Quelle était la différence entre les températures au déjeuner et au coucher du soleil ?
- Réponse
-
La différence de température était de 9 degrés.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
- Identifiez ce que l'on nous demande de trouver.
- Écrivez une phrase qui donne les informations nécessaires pour le trouver.
- Traduisez la phrase en expression.
- Simplifiez l'expression.
- Répondez à la question par une phrase complète.
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner avec des nombres entiers.
- Soustraire des entiers à l'aide de compteurs
Concepts clés
- \[\begin{align} & −a \text{ means the opposite of the number }a \\ & \text{The notation} −a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
- La valeur absolue d'un nombre est sa distance par rapport à 0 sur la ligne numérique.
La valeur absolue d'un nombre n s'écrit comme\(|n|\) et\(|n|≥0\) pour tous les nombres.
Les valeurs absolues sont toujours supérieures ou égales à zéro.
- \[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
- Propriété de soustraction
\(a−b=a+(−b)\)
Soustraire un nombre revient à ajouter son opposé. - Pour la multiplication et la division de deux nombres signés :
Si les signes sont identiques, le résultat est positif.Mêmes signes Résultat • Deux points positifs positif • Deux points négatifs positif
Si les signes sont différents, le résultat est négatif.Différents signes Résultat • Positif et négatif NÉGATIF • Négatif et positif NÉGATIF - Multiplication par\(−1\)
\(−1a=−a\)
Multiplier un nombre par\(−1\) donne son contraire.
- Comment utiliser des nombres entiers dans les applications.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris
- Identifiez ce que l'on nous demande de trouver.
- Écrivez une phrase qui donne les informations nécessaires pour le trouver.
- Traduisez la phrase en expression.
- Simplifiez l'expression.
- Répondez à la question par une phrase complète.
Lexique
- valeur absolue
- La valeur absolue d'un nombre est sa distance par rapport\(0\) à la ligne numérique.
- entiers
- Les nombres entiers et leurs contraires sont appelés entiers.
- nombres négatifs
- Les nombres inférieurs à\(0\) sont des nombres négatifs.
- opposé
- L'opposé d'un nombre est le nombre qui se trouve à la même distance de zéro sur la ligne numérique mais du côté opposé à zéro.


