2.7: 向量代数示例

示例\(\PageIndex{1}\): Analytical Computation of a Resultant

平面\(\vec{C}\)中的三个位移向量\(\vec{A}\)\(\vec{B}\)、和（图 2.3.6）分别由其幅度 A = 10.0、B = 7.0 和 C = 8.0 以及它们各自的方向角指定，水平方向\(\alpha\) = 35°、\(\beta\) = −110° 和\(\gamma\)= 30°。 量级的物理单位是厘米。 将向量解析为其标量分量并找到以下矢量和：

1. \(\vec{R}\)=\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\)，
2. \(\vec{D}\)=\(\vec{A}\) −\(\vec{B}\)，以及
3. \(\vec{S}\)=\(\vec{A}\) − 3\(\vec{B}\) +\(\vec{C}\)。

策略

首先，我们使用方程 2.4.13 来找出每个向量的标量分量，然后以给出的向量分量形式表示每个向量\(\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}\)。 然后，我们使用向量代数的分析方法来寻找结果。

解决方案

我们将给定向量解析为其标量分量：

\[ \begin{cases} A_{x} = A \cos \alpha = (10.0\; cm) \cos {35^{o}} = 8.19\; cm \\ A_{y} = A \sin \alpha = (10.0\; cm) \sin{35^{o}} = 5.73\; cm \end{cases}\]

\[ \begin{cases} B_{x} = B \cos \beta = (7.0\; cm) \cos (-110^{o}) = -2.39\; cm \\ B_{y} = B \sin \beta= (7.0\; cm) \sin (-110^{o}) = -6.58\; cm \end{cases}\]

\[ \begin{cases} C_{x} = C \cos \gamma= (8.0\; cm) \cos (30^{o}) = 6.93\; cm \\ C_{y} = C \sin \gamma= (8.0\; cm) \sin(30^{o}) = 4.00\; cm \end{cases}\]

对于 (a)，我们可以直接代入方程 2.6.7 来找出所得结果的标量分量：

\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = 8.19\; cm - 2.39\; cm + 6.93\; cm = 12.73\; cm \\ R_{y} = A_{y} + B_{y} + C_{y} = 5.73\; cm - 6.58\; cm + 4.00\; cm = 3.15\; cm \end{cases}\]

因此，生成的向量为\(\vec{R} = R_{x} \hat{i} + R_{y} \hat{j} = (12.7 \hat{i} + 3.1 \hat{j})\) cm。 对于 (b)，我们可能希望将向量差写为

\[\vec{D} = \vec{A} - \vec{B} = (A_{x} \hat{i} + A_{y} \hat{j}) - (B_{x} \hat{i} + B_{y} \hat{j}) = (A_{x} - B_{x}) \hat{i} + (A_{y} - B_{y}) \hat{j} \ldotp\]

因此，差值向量为\(\vec{D} = D_{x} \hat{i} + D_{y} \hat{j} = (10.6 \hat{i} + 12.3 \hat{j})\) cm。

对于 (c)，我们可以用以下显式形式写入向量\(\vec{S}\)：

\[ \vec{S} = \vec{A} - 3 \vec{B} + \vec{C} = (A_{x} \hat{i} + A_{y} \hat{j}) - 3(B_{x} \hat{i} + B_{y} \hat{j}) + (C_{x} \hat{i} + C_{y} \hat{j}) = (A_{x} - 3 B_{x} + C_{x}) \hat{i} + (A_{y} - 3 B_{y} + C_{y}) \hat{j} \ldotp\]

然后，的标量分量\(\vec{S}\)是

\[ \begin{cases} S_{x} = A_{x} - 3B_{x} + C_{x} = 8.19\; cm - 3(-2.39\; cm) + 6.93\; cm = 22.29\; cm \\ S_{y} = A_{y} - 3B_{y} + C_{y} = 5.73\; cm -3(-6.58\; cm) + 4.00\; cm = 29.47\; cm \end{cases}\]

向量为\(\vec{S} = S_{x} \hat{i} + S_{y} \hat{j} = (22.3 \hat{i} + 29.5 \hat{j})\) cm。

意义

找到向量分量后，我们可以通过图表来说明向量，或者我们可以计算大小和方向角度，如图所示\(\PageIndex{1}\)。 (b) 和 (c) 中量级的结果可以与使用图形方法获得的相同问题的结果进行比较，如图 2.3.7 和图 2.3. 8 所示。 请注意，分析方法会产生精确的结果，其精度不受标尺或量角器分辨率的限制，就像示例 2.3.2 中用于查找相同结果的图形方法一样。

图\(\PageIndex{1}\)：通过分析获得的解的图形说明。

练习 2.8

三个位移向量\(\vec{A}\)\(\vec{B}\)、和\(\vec{F}\)（图 2.3.6）分别由其幅度 A = 10.00、B = 7.00 和 F = 20.00 指定，以及它们各自的方向角指定，水平方向\(\alpha\) = 35°、\(\beta\) = −110° 和\(\varphi\) = 110°。 量级的物理单位是厘米。 使用分析方法查找向量\(\vec{F}\) =\(\vec{A}\) + 2\(\vec{B}\) −\(\vec{F}\)。 验证 G = 28.15 厘米且\(\theta_{G}\) = −68.65°。

示例\(\PageIndex{2}\): The Tug-of-War Game

四只名为 Astro、Balto、Clifford 和 Dug 的狗用玩具玩拔河游戏（人偶\(\PageIndex{2}\)）。 Astro 向东以南 55° 的方向\(\alpha\)拉动玩具，巴尔托向方向\(\beta\) = 北向东 60° 拉动，克利福德向方向\(\gamma\) = 北向西 55° 拉动。 Astro 以 160.0 单位的力 (N) 进行强力拉动，我们将其缩写为 A = 160.0 N。巴尔托的拉力比 Astro 还要强，大小为 B = 200.0 N，而 Clifford 以 C = 140.0 N 的力拉动玩具时，他的力量会平衡玩具产生的结果其他三种力量，玩具不会向任何方向移动。 Dug 必须用多大的力量向哪个方向拉动玩具才能做到这一点？

图\(\PageIndex{2}\)：四只狗用玩具玩拔河比赛。

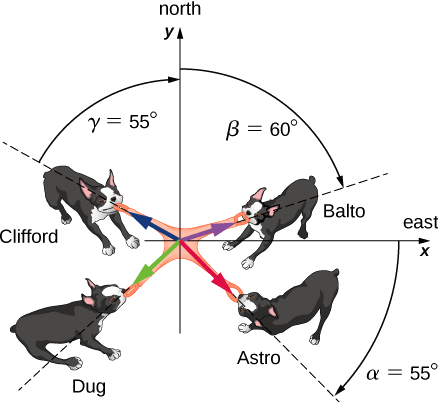
策略

我们假设东方是 x 轴正方向，北方是 y 轴正方向。 如示例所示\(\PageIndex{1}\)，我们必须将三种给定的力——\(\vec{A}\)（来自天文的拉力）、\(\vec{B}\)（来自巴尔托的拉力）和\(\vec{C}\)（来自克利福德的拉力）——解析为它们的标量分量，然后找到合成向量的标量分量\(\vec{R}\) =\(\vec{A}\) +\(\vec{B}\) +\(\vec{C}\)。 当 Dug\(\vec{D}\) 的拉力平衡了这个结果时，\(\vec{D}\)和的总和\(\vec{R}\)必须得出空向量\(\vec{D}\) +\(\vec{R}\) =\(\vec{0}\)。 这意味着\(\vec{D}\) =\(- \vec{R}\) 所以来自 Dug 的拉力必须与之反平行\(\vec{R}\)。

解决方案

方向角为\(\theta_{A}\)\(− \alpha\) = −55°、\(\theta_{B}\) = 90° −\(\beta\) = 30° 和\(\theta_{C}\) = 90° +\(\gamma\) = 145°，将它们代入方程 2.4.13 可以得出三种给定力的标量分量：

\[ \begin{cases} A_{x} = A \cos \theta_{A} = (160.0\; N) \cos (-55^{o}) = + 91.8\; N \\ A_{y} = A \sin \theta_{A} = (160.0\; N) \sin (-55^{o}) = -131.1\; N \end{cases}\]

\[ \begin{cases} B_{x} = B \cos \theta_{B} = (200.0\; N) \cos 30^{o} = + 173.2\; N \\ B_{y} = B \sin \theta_{B} = (200.0\; N) \sin 30^{o} = + 100.0\; N \end{cases}\]

\[ \begin{cases} C_{x} = C \cos \theta_{C} = (140.0\; N) \cos 145^{o} = -114.7\; N \\ C_{y} = C \sin \theta_{C} = (140.0\; N) \sin 145^{o} = + 80.3\; N \end{cases}\]

现在我们计算合成向量的标量分量\(\vec{R} = \vec{A} + \vec{B} + \vec{C}\)：

\[ \begin{cases} R_{x} = A_{x} + B_{x} + C_{x} = + 91.8\; N+ 173.2\; N- 114.7\; N = +150.3 \; N\\ R_{y} = A_{y} + B_{y} + C_{y} = -131.1\; N + 100.0\; N + 80.3\; N= +49.2\; N\end{cases}\]

结果的反平行向量\(\vec{R}\)为

\[\vec{D} = -\vec{R} = -R_{x} \hat{i} - R_{y} \hat{j} = (-150.3 \hat{i} - 49.2 \hat{j}) N \ldotp\]

Dug 的拉力大小是

\[D = \sqrt{D_{x}^{2} + D_{y}^{2}} = \sqrt{(-150.3)^{2} + (-49.2)^{2}} N = 158.1\; N \ldotp\]

Dug 的拉力方向是

\[\theta = \tan^{-1} \left(\dfrac{D_{y}}{D_{x}}\right) = \tan^{-1} \left(\dfrac{-49.2\; N}{-150.3\; N}\right) = \tan^{-1} \left(\dfrac{49.2}{150.3}\right) = 18.1^{o}\ldotp\]

Dug 向西以南 18.1° 的方向拉动，因为两个分量均为负数，这意味着拉力向量位于第三象限中（图 2.4.4）。

练习 2.9

假设 Example 中的 Balto\(\PageIndex{2}\) 离开游戏去处理更重要的事情，但是 Astro、Clifford 和 Dug 继续玩游戏。 Astro 和 Clifford 对玩具的拉力没有改变，但是 Dug 跑来跑去，在另一个地方咬了玩具。 为了平衡 Clifford 和 Astro 的综合拉力，Dug 现在必须用多大的力量向哪个方向拉动玩具？ 通过绘制表示所有相关力量的矢量图来说明这种情况。

示例\(\PageIndex{3}\): Vector Algebra

找出满足方程 2\(\vec{A}\) − 6\(\vec{B}\) + 3\(\vec{C}\) = 2\(\hat{j}\)、= − 2\(\hat{k}\) 和\(\vec{A}\)\(\vec{B}\) =\(\hat{i}\) −\(\hat{j}\) + 的向量\(\vec{C}\)的大小\(\frac{\hat{k}}{2}\)。

策略

我们首先求解未知向量的给定方程\(\vec{C}\)。 然后我们替换\(\vec{A}\) and\(\vec{B}\); 沿三个方向\(\hat{i}\)\(\hat{j}\)、和\(\hat{k}\); 对项进行分组，并确定标量分量 C _x、C _y 和 C _z。 最后，我们用方程式 2.5.6 来求出量级 C。

解决方案

\[\begin{split} 2 \vec{A} - 6 \vec{B} +& 3 \vec{C} = 2 \hat{j}\\ & 3 \vec{C} = 2 \hat{j} - 2 \vec{A} + 6 \vec{B} \\ &\vec{C} = \frac{2}{3} \hat{j} - \frac{2}{3} \vec{A} + 2 \vec{B}\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} (\hat{i} - 2\hat{k}) + 2 \big(- \hat{j} + \frac{\hat{k}}{2}\big)\\ & \quad = \frac{2}{3} \hat{j} - \frac{2}{3} \hat{i} + \frac{4}{3} \hat{k} - 2 \hat{j} + \hat{k}\\ & \quad = -\frac{2}{3} \hat{i} + \big(\frac{2}{3} - 2 \big)\hat{j} + \big(\frac{4}{3}\ + 1 \big)\hat{k}\\ & \quad = -\frac{2}{3} \hat{i} - \frac{4}{3} \hat{j} + \frac{7}{3} \hat{k} \end{split}\]

分量为 C _x =\(-\frac{2}{3}\)、C _y =\(-\frac{4}{3}\) 和 C _z =\(\frac{7}{3}\)，代入方程 2.5.6 得出

\[C = \sqrt{C_{x}^{2} + C_{y}^{2} + C_{z}^{2}} = \sqrt{\left(-\dfrac{2}{3}\right)^{2} + \left(-\dfrac{4}{3}\right)^{2} + \left(\dfrac{7}{3}\right)^{2}} = \sqrt{\frac{23}{3}} \ldotp\]

示例\(\PageIndex{4}\): Displacement of a Skier

从滑雪小屋开始，越野滑雪者向北行驶5.0公里，然后向西行驶3.0公里，最后向西南行驶4.0公里，然后休息。 找到他在休息点时相对于小屋的总位移向量。 他必须从休息点滑多远、朝哪个方向滑雪才能直接返回旅馆？

策略

我们假设一个矩形坐标系，其原点位于滑雪小屋，单位\(\hat{i}\)向量指向东方，单位向量\(\hat{j}\)指向北方。 有三种位移：\(\vec{D}_{1}\)\(\vec{D}_{2}\)、和\(\vec{D}_{3}\)。 我们将它们的大小确定为 D ₁ = 5.0 km、D ₂ = 3.0 km 和 D ₃ = 4.0 km。 我们确定它们的方向是角度\(\theta_{1}\) = 90°、\(\theta_{2}\) = 180° 和\(\theta_{3}\) = 180° + 45° = 225°。 我们将每个位移向量解析为其标量分量，然后将这些分量替换为方程 2.6.5，以获得\(\vec{D}\)从小屋到静止点的合成位移的标量分量。 在从休息点返回小屋的路上，排水量为\(\vec{B}\) = −\(\vec{D}\)。 最后，我们找到了大小和方向\(\vec{B}\)。

解决方案

位移向量的标量分量为

\[ \begin{cases} D_{1x} = D_{1} \cos \theta_{1} = (5.0\; km) \cos 90^{o} = 0 \\ D_{1y} = D_{1} \sin \theta_{1} = (5.0\; km) \sin 90^{o} = 5.0\; km \end{cases}\]

\[ \begin{cases} D_{2x} = D_{2} \cos \theta_{2} = (3.0\; km) \cos 180^{o} = -3.0 \;km\\ D_{2y} = D_{2} \sin \theta_{2} = (3.0\; km) \sin 180^{o} = 0 \end{cases}\]

\[ \begin{cases} D_{3x} = D_{3} \cos \theta_{3} = (4.0\; km) \cos 225^{o} = -2.8\; km \\ D_{3y} = D_{3} \sin \theta_{3} = (4.0\; km) \sin 225^{o} = -2.8\; km \end{cases}\]

净位移向量的标量分量为

\[ \begin{cases} D_{x} = D_{1x} + D_{2x} + D_{3x} = (0 - 3.0 - 2.8)km = -5.8\; km \\ D_{y} = D_{1y} + D_{2y} + D_{3y} = (5.0 + 0 - 2.8)km = + 2.2\; km \end{cases}\]

因此，滑雪者的净位移向量为\(\vec{D}\) = D _x\(\hat{i}\) + D _y\(\hat{j}\) = (−5.8\(\hat{i}\) + 2.2\(\hat{j}\)) km。 在返回小屋的路上，他的位移量为\(\vec{B}\) = −\(\vec{D}\) = − (−5.8\(\hat{i}\) + 2.2\(\hat{j}\)) km = (5.8\(\hat{i}\) − 2.2\(\hat{j}\)) km。 它的大小为 B\(\sqrt{B_{x}^{2} + B_{y}^{2}}\) =\(\sqrt{(5.8)^{2} + (−2.2)^{2}}\) km = 6.2 km，其方向角为\(\theta\) = tan ⁻¹\(\left(\dfrac{−2.2}{5.8}\right)\) = −20.8°。 因此，要返回旅馆，他必须向东部以南约 21° 的方向行驶 6.2 公里。

意义

请注意，通过分析方法解决这个问题不需要任何数字。 使用图形方法时需要图形；但是，我们可以通过草绘来检查解是否合理，这是求解任何向量问题的最后有用步骤。

示例\(\PageIndex{5}\): Displacement of a Jogger

慢跑者跑上了 200 个相同的台阶到达山顶，然后沿着山顶跑 50.0 米，然后在饮水机停下来（图\(\PageIndex{3}\)）。 他从台阶底部的点A到喷泉的B点的位移向量为\(\vec{D}_{AB}\) = (−90.0\(\hat{i}\) + 30.0\(\hat{j}\)) m。飞行中每个台阶的高度和宽度是多少？ 慢跑者的实际行驶距离是多少？ 如果他循环返回到点 A，他的净位移向量是多少？

图\(\PageIndex{3}\)：慢跑者跑上一段台阶。

策略

位移向量\(\vec{D}_{AB}\)是慢跑者\(\vec{D}_{AT}\)沿楼梯的位移向量（从楼梯底部的 A 点到楼梯顶部的 T 点）和他在山顶的位移向量\(\vec{D}_{RB}\)（从楼梯顶部的 T 点到B点的喷泉）。 我们必须找到的水平和垂直分量\(\vec{D}_{TB}\)。 如果每个步骤的宽度 w 和高度 h，则的水平分量的长度\(\vec{D}_{TB}\)必须为 200w，垂直分量的长度必须为 200h。 慢跑者的实际行驶距离是他跑上楼梯的距离和他沿着山顶跑的50.0 m的距离之和。

解决方案

在图中所示的坐标系中\(\PageIndex{3}\)，慢跑者在山顶上的位移向量为\(\vec{D}_{RB}\) = (−50.0 m)\(\hat{i}\)。 他的净位移向量是

\[\vec{D}_{AB} = \vec{D}_{AT} + \vec{D}_{TB} \ldotp \nonumber\]

因此，他\(\vec{D}_{TB}\)沿着楼梯的位移向量为

\[\begin{split} \vec{D}_{AT}& = \vec{D}_{AB} - \vec{D}_{TB} = (-90.0 \hat{i} + 30.0 \hat{j})m - (-50.0 m)\hat{i}) = [(-90.0 50.0) hat{i} + 30.0 \hat{j})]m \\ & = (-40.0 \hat{i} + 30.0 \hat{j})m \ldotp \end{split}\]

它的标量分量是 D _atX = −40.0 m 和 D aT _y = 30.0 m。因此，我们必须有

\[200 w=|-40.0| \mathrm{m} \text { and } 200 h=30.0 \: \mathrm{m} \ldotp \nonumber\]

因此，台阶宽度为 w\(\frac{40.0\; m}{200}\) = 0.2 m = 20 厘米，台阶高度为 w\(\frac{30.0\; m}{200}\) = 0.15 m = 15 cm。 慢跑者沿着楼梯行驶的距离是

\[\vec{D}_{AT} = \sqrt{\vec{D}_{ATx}^{2} + \vec{D}_{ATy}^{2}} = \sqrt{(-40.0)^{2} + (30.0)^{2}}m = 50.0\; m \ldotp \nonumber\]

因此，他跑的实际距离为 D A _T + D _TB = 50.0 m + 50.0 m = 100.0 m。当他循环并从喷泉回到 A 点的初始位置时，他覆盖的总距离是这个距离的两倍，即 200.0 m。但是，他的净位移向量为零，因为当其最终位置与初始位置相同时，其净位移向量的标量分量为零（方程 2.4.4）。

在许多物理环境中，我们经常需要知道向量的方向。 例如，我们可能想知道某个点的磁场矢量的方向或物体的运动方向。 我们已经说过方向是由单位向量给出的，它是一个无量纲的实体，也就是说，它没有与之相关的物理单位。 当有问题的向量位于笛卡尔坐标系中的一个轴上时，答案很简单，因为那样的话，它的方向单位向量要么平行，要么与轴的单位向量的方向平行，要么反平行。 例如，向量方向\(\vec{d}\) = -5 m\(\hat{i}\) 是单位向量\(\vec{d}\) =-\(\hat{i}\)。 找到任何向量的方向单位向\(\vec{V}\)量的一般规则\(\vec{V}\)是将其除以其量级 V：

\[\widehat{\mathbf{V}}=\frac{\overrightarrow{\mathbf{V}}}{V} \label{2.26} \cdot \]

从这个表达式中我们可以看出，方向的单位向量确实是无量纲的，因为方程\ ref {2.26} 中的分子和分母具有相同的物理单位。 通过这种方式，方程\ ref {2.26} 允许我们用轴的单位向量来表示方向的单位向量。 以下示例说明了这个原理。

示例\(\PageIndex{6}\): The Unit Vector of Direction

如果示例 2.6.1 中军事车队的速度矢量为\(\vec{v}\) = (4.000\(\hat{i}\) + 3.000\(\hat{j}\) + 0.100\(\hat{k}\)) km/h，则其运动方向的单位向量是多少。

策略

车队运动方向的单位向量是平行\(\hat{v}\)于速度矢量的单位向量。 根据方程\ ref {2.26}，单位向量是通过将向量除以其大小获得的。

解决方案

向量的大小\(\vec{v}\)为

\[v = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}} = \sqrt{4.000^{2} + 3.000^{2} + 0.100^{2}}km/h = 5.001\; km/h \ldotp \nonumber\]

要获得单位向量\(\hat{v}\)，请除\(\vec{v}\)以其大小：

\[\begin{split} \hat{v}& = \frac{\vec{v}}{v} = \frac{(4.000 \hat{i} + 3.00 \hat{j} + 0.100 \hat{k})km/h}{5.001\; km/h} \\ & = \frac{(4.000 \hat{i} + 3.000 \hat{j} + 0.1100 \hat{k})}{5.001} \\ & = \frac{4.000}{5.001} \hat{i} + \frac{3.000}{5.001} \hat{j} + \frac{0.100}{5.001} \hat{k} \\ & = (79.98 \hat{i} + 59.99 \hat{j} + 2.00 \hat{k}) \times 10^{-2} \ldotp \end{split}\]

意义

请注意，将分析方法与计算器一起使用时，建议至少将计算到小数点后三位，然后将最终答案四舍五入到所需的有效数字数，这是我们在本示例中执行计算的方式。 如果您过早地对部分答案进行四舍五入，则最终答案可能会出现巨大的数值误差，而且可能与确切答案或实验中测得的值相去甚远。

练习 2.10

通过计算示例中\(\hat{v}\)获得的向量的大小来验证其确实\(\PageIndex{3}\)是单位向量。 如果示例 2.6.1 中的车队正在沙漠平地上移动，也就是说，如果其速度的第三个分量为零，则其运动方向的单位向量是多少？ 它代表哪个地理方向？