10.1:使用平方根属性求解二次方程
- Page ID
- 204537
在本节结束时,您将能够:
- \(ax^2=k\)使用平方根属性求解形式的二次方程
- \(a(x−h)^2=k\)使用平方根属性求解形式的二次方程
在@@
- 简化:\(\sqrt{75}\)。
- 简化:\(\sqrt{\dfrac{64}{3}}\)
- 因子:\(4x^{2} − 12x + 9\)。
二次方程是形式的方程式\(ax^{2} + bx + c = 0\),其中\(a \neq 0\)。 它们与线性方程的不同之处在于,它们包含一个将变量提高到二次幂的项。 我们使用与线性方程不同的方法来求解二次方程 s,因为仅仅相加、减去、乘和除项并不能隔离变量。
我们已经看到,一些二次方程可以通过分解来求解。 在本章中,我们将使用其他三种方法来求解二次方程。
\(ax^2=k\)使用平方根属性求解形式的二次方程
我们已经通过分解求解了一些二次方程。 让我们回顾一下我们是如何使用分解来求解二次方程的\(x^{2} = 9\)。
\[\begin{array}{ll} {}&{x^2=9}\\ {\text{Put the equation in standard form.}}&{x^2−9=0}\\ {\text{Factor the left side.}}&{(x - 3)(x + 3) = 0}\\ {\text{Use the Zero Product Property.}}&{(x - 3) = 0, (x + 3) = 0}\\ {\text{Solve each equation.}}&{x = 3, x = -3}\\ {\text{Combine the two solutions into} \pm \text{form}}&{x=\pm 3}\\ \nonumber \end{array}\]
(解读\(x\)为 “等于正或负”\(3\)。)
我们可以很容易地使用因子分解来找到相似方程的解,比如\(x^{2}=16\)和\(x^{2} = 25\),因为\(16\)和\(25\)是完美的正方形。 但是当我们有这样的方程式时会发生什么\(x^{2}=7\)? 由于\(7\)不是完美的正方形,因此我们无法通过分解来求解方程。
这些方程都是形式上的\(x^{2}=k\)。
我们用这种方式定义了数字的平方根:
如果\(n^{2} = m\),\(n\)则为的平方根\(m\)。
这就产生了平方根属性。
如果\(x^{2}=k\)、和\(k \geq 0\)、然后\(x = \sqrt{k}\)或\(x = -\sqrt{k}\)。
请注意,平方根属性为形式的方程给出了两个解\(x^2=k\):k 的主平方根及其对立面。 我们也可以将解决方案写成\(x=\pm \sqrt{k}\)
现在,我们将\(x^{2} = 9\)再次求解方程,这次是使用平方根属性。
\[\begin{array}{ll} {}&{x^{2} = 9}\\ {\text{Use the Square Root Property.}}&{x = \pm\sqrt{9}}\\ {\text{Simplify the radical.}}&{x = \pm 3}\\ {\text{Rewrite to show the two solutions.}}&{x = 3, x = −3}\\ \nonumber \end{array}\]
当常量不是完美正方形时会发生什么? 让我们使用平方根属性来求解方程\(x^2=7\)。
\[\begin{array} {ll} {\text{Use the Square Root Property. }}&{x = \pm\sqrt{7}}\\ {\text{Rewrite to show two solutions.}}&{x = \sqrt{7}, x = −\sqrt{7}}\\ {\text{We cannot simplify} \sqrt{7} \text{ so we leave the answer as a radical.}}&{}\\ \nonumber \end{array}\]
解决:\(x^{2} = 169\)
- 回答
-
\[\begin{array}{ll} {}&{x^2=169}\\ {\text{Use the Square Root Property.}}&{x=\pm\sqrt{169}}\\ {\text{Simplify the radical.}}&{x = \pm13}\\{\text{Rewrite to show two solutions.}}&{x = 13, x = −13}\\ \nonumber \end{array}\]
解决:\(x^2=81\)
- 回答
-
x=9,x=−9
解决:\(y^{2} = 121\)
- 回答
-
y = 11,y = −11
如何\(ax^{2} = k\)使用平方根属性求解这种形式的二次方程
解决:\(x^{2} − 48 = 0\)
- 回答




解决:\(x^{2} − 50 = 0\)
- 回答
-
\(x = 5\sqrt{2}, x = −5\sqrt{2}\)
解决:\(y^{2} − 27 = 0\)
- 回答
-
\(y = 3\sqrt{3}, x = −3\sqrt{3}\)
- 分离二次项并将其系数设为一。
- 使用平方根属性。
- 简化激进。
- 检查解决方案。
要使用平方根属性,变量项的系数必须等于 1。 在下一个示例中,在使用平方根属性之前,我们必须将方程的两边除以 5。
解决:\(5m^2=80\)
- 回答
-
二次项是孤立的。 \(5m^2=80\) 除以 5 得出 cofficient 1。 \(\frac{5m^2}{5}=\frac{80}{5}\) 简化。 \(m^2=16\) 使用平方根属性。 \(m=\pm\sqrt{16}\) 简化激进。 \(m=\pm 4\) 重写以显示两个解决方案。 m=4,m=−4 检查解决方案。
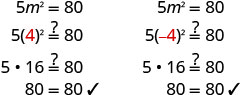
解决:\(2x^2=98\)。
- 回答
-
x=7,x=−7
解决:\(3z^2=108\)。
- 回答
-
z=6,z=−6
平方根属性以表示 “\(x^2=k\)If an\(k\ge 0\) d” 开头。 如果会发生什么\(k<0\)? 在下一个示例中,情况将如此。
解决:\(q^2+24=0\)。
- 回答
-
\[\begin{array}{ll} {}&{q^2=24}\\ {\text{Isolate the quadratic term.}}&{q^2=−24}\\ {\text{Use the Square Root Property.}}&{q=\pm\sqrt{-24}}\\ {\text{The} \sqrt{-24} \text{is not a real number}}& {\text{There is no real solution}}\\ \nonumber \end{array}\]
解决:\(c^2+12=0\)。
- 回答
-
没有真正的解决方案
解决:\(d^2+81=0\)。
- 回答
-
没有真正的解决方案
解决:\(\frac{2}{3}u^2+5=17\)。
- 回答
-
\(\frac{2}{3}u^2+5=17\) 分离二次项。 \(\frac{2}{3}u^2=12\)
乘\(\frac{3}{2}\)以得出系数 1。 \(\frac{3}{2}·\frac{2}{3}u^2=\frac{3}{2}·12\) 简化。 \(u^2=18\) 使用平方根属性。 \(u=\pm\sqrt{18}\) 简化激进。 \(u=\pm\sqrt{9}\sqrt{2}\) 简化。 \(u=\pm3\sqrt{2}\) 重写以显示两个解决方案。 \(u=3\sqrt{2}\),\(u=−3\sqrt{2}\) 查看。
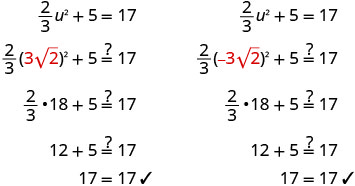
解决:\(\frac{1}{2}x^2+4=24\)
- 回答
-
\(x=2\sqrt{10}\),\(x=−2\sqrt{10}\)
解决:\(\frac{3}{4}y^2−3=18\)。
- 回答
-
\(y=2\sqrt{7}\),\(y=−2\sqrt{7}\)
某些方程的解在自由基内部可能有分数。 当这种情况发生时,我们必须使分母合理化。
解决:\(2c^2−4=45\)。
- 回答
-
\(2c^2−4=45\) 分离二次项。 \(2c^2=49\) 除以 2 得出系数 1。 \(\frac{2c^2}{2}=\frac{49}{2}\) 简化。 \(c^2=\frac{49}{2}\) 使用平方根属性。 \(c=\pm\frac{\sqrt{49}}{\sqrt{2}}\) 简化激进。 \(c=\pm\frac{\sqrt{49}}{\sqrt{2}}\) 合理化分母。 \(c=\pm\frac{\sqrt{49}\sqrt{2}}{\sqrt{2}\sqrt{2}}\) 简化。 \(c=\pm\frac{7\sqrt{2}}{2}\) 重写以显示两个解决方案。 \(c=\frac{7\sqrt{2}}{2}\),\(c=−\frac{7\sqrt{2}}{2}\) 查看。 我们把支票留给你。
解决:\(5r^2−2=34\)。
- 回答
-
\(r=\frac{6\sqrt{5}}{5}\),\(r=−\frac{6\sqrt{5}}{5}\)
解决:\(3t^2+6=70\)。
- 回答
-
\(t=\frac{8\sqrt{3}}{3}\),\(t=−\frac{8\sqrt{3}}{3}\)
\(a(x-h)^2=k\)使用平方根属性求解形式的二次方程
我们也可以使用平方根属性来求解方程。\((x−3)^2=16\) 我们将整个二项式 (x−3) 视为二次项。
解决:\((x−3)^2=16\)。
- 回答
-
\((x−3)^2=16\) 使用平方根属性。 \(x−3=\pm\sqrt{16}\) 简化。 \(x−3=\pm 4\) 写成两个方程式。 \(x−3=4\),\(x−3=−4\) 解决。 x=7,x=−1 查看。
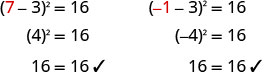
解决:\((q+5)^2=1\)。
- 回答
-
q=−6,q=−4
解决:\((r−3)^2=25\)。
- 回答
-
r=8,r=−2
解决:\((y−7)^2=12\)。
- 回答
-
\((y−7)^2=12\)。 使用平方根属性。 \(y−7=\pm\sqrt{12}\) 简化激进。 \(y−7=\pm2\sqrt{3}\) 求解 y。 \(y=7\pm2\sqrt{3}\) 重写以显示两个解决方案。 \(y=7+2\sqrt{3}\),\(y=7−2\sqrt{3}\) 查看。

解决:\((a−3)^2=18\)。
- 回答
-
\(a=3+3\sqrt{2}\),\(a=3−3\sqrt{2}\)
解决:\((b+2)^2=40\)。
- 回答
-
\(b=−2+2\sqrt{10}\),\(b=−2−2\sqrt{10}\)
解决:\((x−\frac{1}{2})^2=\frac{5}{4}\)。
- 回答
-
\((x−\frac{1}{2})^2=\frac{5}{4}\) 使用平方根属性。 \((x−\frac{1}{2})=\pm\sqrt\frac{5}{4}\) 将基数重写为平方根的分数。 \((x−\frac{1}{2})=\pm\frac{\sqrt{5}}{\sqrt{4}}\) 简化激进。 \((x−\frac{1}{2})=\pm\frac{\sqrt{5}}{2}\) 求解 x。 \(x=\frac{1}{2}+\pm\frac{\sqrt{5}}{2}\) 重写以显示两个解决方案。 \(x=\frac{1}{2}+\frac{\sqrt{5}}{2}\),\(x=\frac{1}{2}−\frac{\sqrt{5}}{2}\) 查看。 我们把支票留给你
解决:\((x−\frac{1}{3})^2=\frac{5}{9}\)。
- 回答
-
\(x=\frac{1}{3}+\frac{\sqrt{5}}{3}\),\(x=\frac{1}{3}−\frac{\sqrt{5}}{3}\)
解决:\((y−\frac{3}{4})^2=\frac{7}{16}\)。
- 回答
-
\(y=\frac{3}{4}+\frac{\sqrt{7}}{4}\),\(y=\frac{3}{4}−\frac{\sqrt{7}}{4}\),
我们将通过隔离二项式来开始下一个示例的解。
解决:\((x−2)^2+3=30\)。
- 回答
-
\((x−2)^2+3=30\) 分离二项式项。 \((x−2)^2=27\) 使用平方根属性。 \(x−2=\pm\sqrt{27}\) 简化激进。 \(x−2=\pm3\sqrt{3}\) 求解 x。 \(x=2+\pm3\sqrt{3}\) \(x−2=\pm3\sqrt{3}\) \(x=2+3\sqrt{3}\),\(x=2−3\sqrt{3}\) 查看。 我们把支票留给你
解决:\((a−5)^2+4=24\)。
- 回答
-
\(a=5+2\sqrt{5}\),\(a=5−2\sqrt{5}\)
解决:\((b−3)^2−8=24\)。
- 回答
-
\(b=3+4\sqrt{2}\),\(b=3−4\sqrt{2}\)
解决:\((3v−7)^2=−12\)。
- 回答
-
\((3v−7)^2=−12\) 使用平方根属性。 \(3v−7=\pm\sqrt{−12}\) \(\sqrt{−12}\)不是实数。 没有真正的解决方案。
解决:\((3r+4)^2=−8\)。
- 回答
-
没有真正的解决方案
在接下来的两个例子中,方程的左边似乎不是这种形式\(a(x−h)^2\)。 但是它们是完美的正方三项式,所以我们会考虑把它们变成我们需要的形式。
解决:\(p^2−10p+25=18\)。
- 回答
-
方程的左侧是一个完美的方形三项式。 我们将首先将其考虑在内。
\(p^2−10p+25=18\) 将完美的正方三项式分解出来。 \((p−5)^2=18\) 使用平方根属性。 \(p−5=\pm\sqrt{18}\) 简化激进。 \(p−5=\pm3\sqrt{2}\) 求解 p。 \(p=5\pm3\sqrt{2}\) 重写以显示两个解决方案。 \(p=5+3\sqrt{2}\),\(p=5−3\sqrt{2}\) 查看。 我们把支票留给你。
解决:\(x^2−6x+9=12\)。
- 回答
-
\(x=3+2\sqrt{3}\),\(x=3−2\sqrt{3}\)
解决:\(y^2+12y+36=32\)。
- 回答
-
\(y=−6+4\sqrt{2}\),\(y=−6−4\sqrt{2}\)
解决:\(4n^2+4n+1=16\)。
- 回答
-
同样,我们注意到方程的左侧是一个完美的方形三项式。 我们将首先将其考虑在内。
\(4n^2+4n+1=16\) 将完美的正方三项式分解出来。 \((2n+1)^2=16\) 使用平方根属性。 \((2n+1)=\pm\sqrt{16}\) 简化激进。 \((2n+1)=\pm4\) 求解 n。 \(2n=−1\pm4\) 将每边除以 2。 \(\frac{2n}{2}=\frac{−1\pm4}{2}\)
\(n=\frac{−1\pm4}{2}\)
重写以显示两个解决方案。 \(n=\frac{−1+4}{2}\),\(n=\frac{−1−4}{2}\) 简化每个方程。 \(n=\frac{3}{2}\),\(n=−\frac{5}{2}\) 查看。
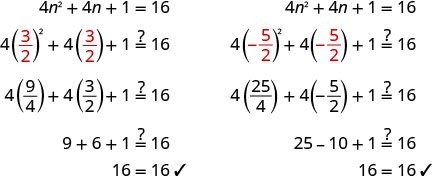
解决:\(9m^2−12m+4=25\)。
- 回答
-
\(m=\frac{7}{3}\),\(m=−1\)
解决:\(16n^2+40n+25=4\)。
- 回答
-
\(n=−\frac{3}{4}\), \(n=−\frac{7}{4}\)
访问以下在线资源,获取有关求解二次方程的更多指导和练习:
- 求解二次方程:取平方根求解
- 使用平方根求解二次方程
- 求解二次方程:平方根法
关键概念
- 平方根属性 I
f\(x^2=k\)、and\(k\ge 0\)、then\(x=\sqrt{k}\) or\(x=−\sqrt{k}\)。
词汇表
- 二次方程
- 二次方程是形式\(ax^2+bx+c=0\)为 where 的方程\(a \ne 0\)。
- 平方根属性
- 平方根属性指出 if、an\(x^2=k\) d\(k\ge 0\)、then\(x=\sqrt{k}\) or\(x=−\sqrt{k}\)。


