9.6: 用平方根求解方程
- Page ID
- 204412
在本节结束时,您将能够:
- 求解激进方程
- 在应用程序中使用平方根
求解激进方程
在本节中,我们将求解以平方根的基数为变量的方程。 这种类型的方程称为激进方程。
变量位于平方根的基数中的方程称为激进方程。
像往常一样,在求解这些方程时,我们对方程的一侧所做的事情也必须对另一侧做的事情。 由于求平量和取平方根是 “相反的” 运算,因此我们将对两边进行平方,以移除激进符号并求解内部变量。
但是请记住,当我们写作时,\(\sqrt{a}\)我们指的是主平方根。 所以\(\sqrt{a} \ge 0\)总是这样。 当我们通过将两边求平来求解激进方程时,我们可能会得到一个代数解,该解会为\(\sqrt{a}\)负数。 这个代数解不是原始激进方程的解;它是一个无关的解。 当我们求解有理方程时,我们也看到了无关的解。
对于方程式\(\sqrt{x+2}=x\):
- x=2 是解决方案吗?
- x=−1 是一个解决方案吗?
- 回答
-
1。 x=2 是解决方案吗?
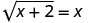
假设 x = 2。 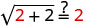
简化。 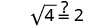
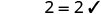
2 是一个解决方案。 2。 x=−1 是一个解决方案吗?
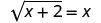
假设 x = −1。 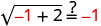
简化。 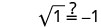
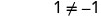
−1 不是解。 −1 是方程的外来解。
对于方程式\(\sqrt{x+6}=x\):
- x=−2 是解决方案吗?
- x=3 是解决方案吗?
- 回答
-
- 不
- 是的
对于方程式\(\sqrt{−x+2}=x\):
- x=−2 是解决方案吗?
- x=1 是解决方案吗?
- 回答
-
- 不
- 是的
对于\(a \ge 0\),\((\sqrt{a})^2=a\)
如何求解激进方程
解决:\(\sqrt{2x−1}=7\)
- 回答
-
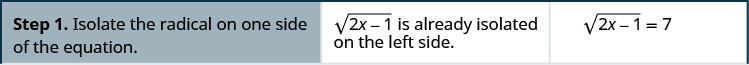



解决:\(\sqrt{3x−5}=5\)。
- 回答
-
10
解决:\(\sqrt{4x+8}=6\)。
- 回答
-
7
- 分离方程一侧的自由基。
- 对方程的两边进行平方。
- 求解新方程。
- 检查答案。
解决:\(\sqrt{5n−4}−9=0\)。
- 回答
-
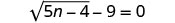
要隔离激进分子,请在两边加上 9。 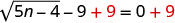
简化。 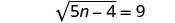
对方程的两边进行平方。 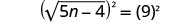
求解新方程。 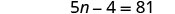


检查答案。

解是 n = 17。
解决:\(\sqrt{3m+2}−5=0\)。
- 回答
-
\(\frac{23}{3}\)
解决:\(\sqrt{10z+1}−2=0\)。
- 回答
-
\(\frac{3}{10}\)
解决:\(\sqrt{3y+5}+2=5\)。
- 回答
-
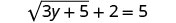
要隔离根部,请从两边减去 2。 
简化。 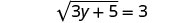
对方程的两边进行平方。 
求解新方程。 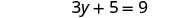

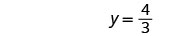
检查答案。
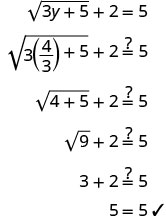
解决的办法是\(y=\frac{4}{3}\)
解决:\(\sqrt{3p+3}+3=5\)。
- 回答
-
\(\frac{1}{3}\)
解决:\(\sqrt{5q+1}+4=6\)。
- 回答
-
\(\frac{3}{5}\)
当我们使用激进符号时,我们指的是主根或正根。 如果一个方程的平方根等于负数,则该方程将没有解。
解决:\(\sqrt{9k−2}+1=0\)。
- 回答
-
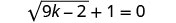
要隔离根部,请从两边减去 1。 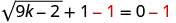
简化。 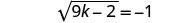
由于平方根等于负数,因此方程没有解。
解决:\(\sqrt{2r−3}+5=0\)
- 回答
-
没有解决办法
解决:\(\sqrt{7s−3}+2=0\)。
- 回答
-
没有解决办法
\[\begin{array}{cc} {(a+b)^2=a^2+2ab+b^2}&{(a−b)^2=a^2−2ab+b^2}\\ \nonumber \end{array}\]
别忘了中间学期!
解决:\(\sqrt{p−1}+1=p\)。
- 回答
-
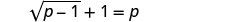
要隔离根部,请从两边减去 1。 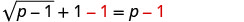
简化。 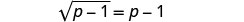
对方程的两边进行平方。 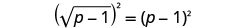
简化,然后求解新方程。 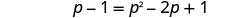
它是一个二次方程,所以在一边求零。 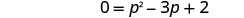
将右侧考虑在内。 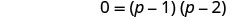
使用零乘积属性。 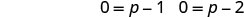
求解每个方程。 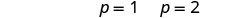
查看答案。
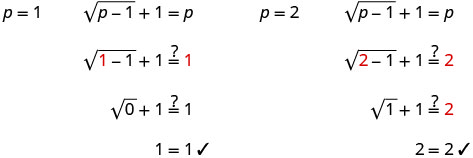
解是 p = 1,p = 2。
解决:\(\sqrt{x−2}+2=x\)。
- 回答
-
2、3
解决:\(\sqrt{y−5}+5=y\)。
- 回答
-
5、6
解决:\(\sqrt{r+4}−r+2=0\)。
- 回答
-
\(\sqrt{r+4}−r+2=0\) 隔离激进分子。 \(\sqrt{r+4}=r−2\) 对方程的两边进行平方。 \((\sqrt{r+4})^2=(r−2)^2\) 求解新方程。 \(r+4=r^2−4r+4\) 它是一个二次方程,所以在一边求零。 \(0=r^2−5r\) 将右侧考虑在内。 \(0=r(r−5)\) 使用零乘积属性。 0=r 0=r−5 求解方程。 r=0 r=5 检查答案。
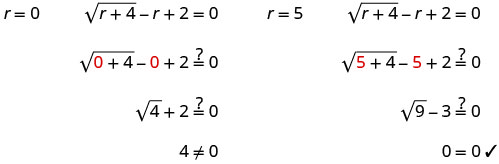
r=5 r=0 是一个无关的解。
解决:\(\sqrt{m+9}−m+3=0\)。
- 回答
-
7
解决:\(\sqrt{n+1}−n+1=0\)
- 回答
-
3
当激进前面有一个系数时,我们也必须将其平方。
解决:\(3\sqrt{3x−5}−8=4\)。
- 回答
-
\(3\sqrt{3x−5}−8=4\) 隔离激进分子。 \(3\sqrt{3x−5}=12\) 对方程的两边进行平方。 \((3\sqrt{3x−5})^2=(12)^2\) 简化,然后求解新方程。 9 (3x−5) =144 分发。 27x−45=144 求解方程。 27x=189 x=7 检查答案。
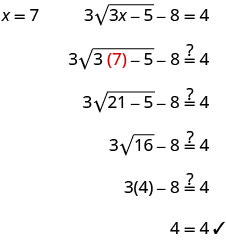
解决方案是 x=7。
解决:\(\sqrt{24a+2}−16=16\)。
- 回答
-
\(\frac{127}{2}\)
解决:\(\sqrt{36b+3}−25=50\)。
- 回答
-
\(\frac{311}{3}\)
解决:\(\sqrt{4z−3}=\sqrt{3z+2}\)。
- 回答
-
\(\sqrt{4z−3}=\sqrt{3z+2}\) 激进的术语是孤立的 \(\sqrt{4z−3}=\sqrt{3z+2}\) 对方程的两边进行平方。 \((\sqrt{4z−3})^2=(\sqrt{3z+2})^2\) 简化,然后求解新方程 4z−3=3z+2 z−3=2 z=5 x=7 检查答案。
我们留给你出示 5 张支票!
解是 z=5。
解决:\(\sqrt{2x−5}=\sqrt{5x+3}\)。
- 回答
-
没有解决办法
解决:\(\sqrt{7y+1}=\sqrt{2y−5}\)。
- 回答
-
没有解决办法
有时候,在对方程的两边进行平方之后,我们在激进内部还有一个变量。 发生这种情况时,我们重复程序的第 1 步和第 2 步。 我们将方程的两边分离出来,然后再平方。
解决:\(\sqrt{m}+1=\sqrt{m+9}\)。
- 回答
-
\(\sqrt{m}+1=\sqrt{m+9}\) 右边的激进分子是孤立的。
两边都是正方形
\((\sqrt{m}+1)^2=(\sqrt{m+9})^2\) 简化——乘法时要非常小心! \(m+2\sqrt{m}+1=m+9\) 方程式中还有一个激进分子。
因此,我们必须重复前面的步骤。 隔离激进分子。
\(2\sqrt{m}=8\) 两边都是正方形。 \((2\sqrt{m})^2=(8)^2\) 简化,然后求解新方程。 4m=64 m=16 检查答案。
我们留给你来证明那张 m=16 支票!
解决方案是 m=16。
解决:\(\sqrt{x}+3=\sqrt{x+5}\)。
- 回答
-
没有解决办法
解决:\(\sqrt{m}+5=\sqrt{m+16}\)。
- 回答
-
没有解决办法
解决:\(\sqrt{q−2}+3=\sqrt{4q+1}\)。
- 回答
-
\(\sqrt{q−2}+3=\sqrt{4q+1}\) 右边的激进分子是孤立的。
两边都是正方形
\((\sqrt{q−2}+3)^2=(\sqrt{4q+1})^2\) 简化。 \(q−2+6\sqrt{q−2}+9=4q+1\) 方程式中还有一个激进分子。
因此,我们必须重复前面的步骤。 隔离激进分子。
\(6\sqrt{q−2}=3q−6\) 两边都是正方形。 \((6\sqrt{q−2})^2=(3q−6)^2\) 简化,然后求解新方程。 \(36(q−2)=9q^2−36q+36\) 分发。 \(36q−72=9q^2−36q+36\) 它是一个二次方程,所以在一边求零。 \(0=9q^2−72q+108\) 将右侧考虑在内。 \(0=9(q^2−8q+12)\)
\(0=9(q−6)(q−2)\)
使用零乘积属性 \[\begin{array}{ll} {q−6=0}&{q−2=0}\\ {q=6}&{q=2}\\ \nonumber \end{array}\] 支票留给你了。 (两种解决方案都应该有效。)
解是 q=6 和 q=2。
解决:\(\sqrt{y−3}+2=\sqrt{4y+2}\)。
- 回答
-
没有解决办法
解决:\(\sqrt{n−4}+5=\sqrt{3n+3}\)。
- 回答
-
没有解决办法
在应用程序中使用平方根
随着大学课程的进展,你会遇到在许多学科中都包含平方根的公式。 我们已经使用公式来求解几何应用程序。
我们将使用几何应用程序的问题解决策略,稍作修改,为我们提供一个使用任何学科公式求解应用程序的计划。
- 阅读问题并确保所有文字和想法都被理解。 在适当的时候,画一个图形并用给定的信息贴上标签。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 命名它。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
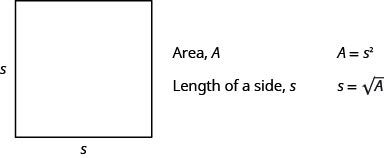
我们使用公式 A=L·W 来求出长度为 L 、宽 W 的矩形的面积。 正方形是长度和宽度相等的矩形。 如果我们将 s 设为正方形边的长度,则正方形的面积为\(s^2\)。
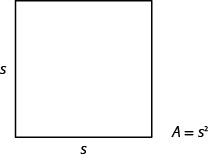
如果我们知道边的长度,则该公式会\(A=s^2\)给出正方形的面积。 如果我们想找到给定区域的一条边的长度怎么办? 然后我们需要求解 s 的方程。
\[\begin{array}{ll} {}&{A=s^2}\\ {\text{Take the square root of both sides.}}&{\sqrt{A}=\sqrt{s^2}}\\ {\text{Simplify.}}&{s=\sqrt{A}}\\ \nonumber \end{array}\]
我们可以使用这个公式\(s=\sqrt{A}\)来计算给定面积的正方形边的长度。
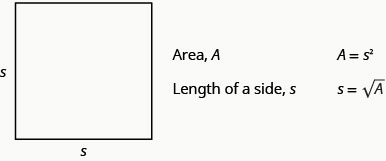
我们将在下一个示例中举一个这样的例子。
Mike 和 Lychelle 想做一个方形露台。 他们有足够的混凝土来铺设 200 平方英尺的面积。 使用公式计算\(s=\sqrt{A}\)露台两侧的长度。 将答案四舍五入到最接近的十分之一英尺。
- 回答
-
第 1 步。 阅读问题。 画一个图形并用给定的信息贴上
标签。
A = 200 平方英尺 第 2 步。 确定你在找什么。 方形露台一侧的长度。 第 3 步。 通过
选择一个变量来表示你要找的东西来命名它。假设 s = 边的长度。 第 4 步。 通过编写
适合情况的公式或模型将其转换为方程。
替换给定的信息。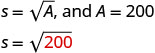
第 5 步。 使用良好的代数
技巧求解方程。 四舍五入到小数点后一位。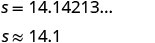
第 6 步。 检查问题中的答案并
确保答案合理。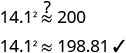
这已经足够接近了,因为我们四舍五入了
平方根。
侧面为 14.1 英尺的露台是否合理?
是的。第 7 步。 用完整的
句子回答问题。露台的两侧应为 14.1 英尺。
凯蒂想在她的前院种一块方形草坪。 她有足够的草皮覆盖370平方英尺的面积。 使用公式计算\(s=\sqrt{A}\)草坪两侧的长度。 将答案四舍五入到最接近的十分之一英尺。
- 回答
-
19.2 英尺
塞尔吉奥想制作一个方形的马赛克作为他正在建造的桌子的镶嵌物。 他有足够的瓷砖覆盖2704平方厘米的面积。 使用公式\(s=\sqrt{A}\)求出他的马赛克每边的长度。 将答案四舍五入到最接近的十分之一英尺。
- 回答
-
52.0 厘米
平方根的另一种应用与重力有关。
在地球上,如果物体从 hh feet 的高度掉落,则使用以下公式得出到达地面所需的时间(以秒为单位)
\(t=\frac{\sqrt{h}}{4}\)
例如,如果一个物体从 64 英尺的高度掉落,我们可以通过在公式中替换 h=64 来计算到达地面所需的时间。
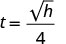 |
|
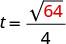 |
|
| 以 64 的平方根为例。 | 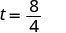 |
| 简化分数。 | 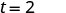 |
从 64 英尺高处掉落的物体需要 2 秒钟才能到达地面。
克里斯蒂把太阳镜从河上方400英尺的一座桥上掉下来。 使用公式计算\(t=\frac{\sqrt{h}}{4}\)太阳镜到达河里花了多少秒钟。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 太阳镜到达河里所花费
的时间。第 3 步。 通过
选择一个变量来表示你要找的东西来命名它。让 t = 时间。 第 4 步。 通过编写
适合情况的公式或模型将其转换为方程。
在给定的信息中替换。

第 5 步。 使用良好的代数
技巧求解方程。

第 6 步。 检查问题中的答案并
确保答案合理。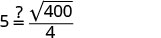

5=5 ✓5 秒钟看起来合理吗?
是的。第 7 步。 用完整的
句子回答问题。太阳镜落水需要 5 秒钟。
一架直升机从1,296英尺的高度投下了一个救援包。 使用公式计算\(t=\frac{\sqrt{h}}{4}\)包裹到达地面花了多少秒。
- 回答
-
9 秒
洗窗器从人行道上方 196 英尺的平台上掉了一\(t=\frac{\sqrt{h}}{4}\)把刮刀使用公式计算刮刀到达人行道花了多少秒钟。
- 回答
-
3.5 秒
调查车祸的警官测量人行道上防滑痕迹的长度。 然后,他们使用平方根来确定汽车在刹车前行驶的速度,以英里/小时为单位。
如果防滑痕迹的长度为 d 英尺,则可以使用以下公式得出刹车前汽车的速度 s
\(s=\sqrt{24d}\)
车祸发生后,一辆汽车的防滑痕迹长达 190 英尺。 在施加制动之前,使用该公式\(s=\sqrt{24d}\)找出汽车的速度。 将答案四舍五入到最接近的十分之一。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 汽车的速度。 第 3 步。 说出我们要找的东西。 假设 s = 速度。 第 4 步。 通过编写相应的公式将其@@ 转换为方程。 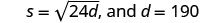
替换给定的信息。 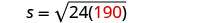
第 5 步。 求解方程。 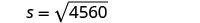
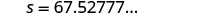
四舍五入到小数点后一位。 
第 6 步。 检查问题中的答案。
67.5β? 24 (190)
67.5? 4560
67.5? 67.5277...67.5 英里/小时是合理的速度吗? 是的。 第 7 步。 用完整的句子@@ 回答问题。 汽车的速度约为每小时 67.5 英里。
事故调查员测量了汽车的防滑痕迹。 防滑痕迹的长度为 76 英尺。 在施加制动之前,使用该公式\(s=\sqrt{24d}\)找出汽车的速度。 将答案四舍五入到最接近的十分之一。
- 回答
-
42.7 英尺
发生事故的车辆的防滑痕迹长达 122 英尺。 在施加制动之前,使用该公式\(s=\sqrt{24d}\)找出车辆的速度。 将答案四舍五入到最接近的十分之一。
- 回答
-
54.1 英尺
关键概念
- 要求解激进方程:
- 分离方程一侧的自由基。
- 对方程的两边进行平方。
- 求解新方程。
- 检查答案。 获得的某些解在原始方程中可能不起作用。
- 使用公式求解应用程序
- 阅读问题并确保所有文字和想法都被理解。 在适当的时候,画一个图形并用给定的信息贴上标签。
- 确定我们在寻找什么。
- 通过选择一个变量来表示我们要找的东西来@@ 命名它。
- 通过编写适合情况的公式或模型将其@@ 转换为方程。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
- 正方形的面积
- 坠落物体
- 在地球上,如果物体从 hh feet 的高度掉落,则使用公式得出到达地面所需的时间(以秒为单位)\(t=\frac{\sqrt{h}}{4}\)。
- 汽车的防滑痕迹和速度
- 如果防滑痕迹的长度为 d 英尺,则可以使用公式得出刹车前汽车的速度 s\(s=\sqrt{24d}\)。
词汇表
- 激进方程
- 变量位于平方根的基数中的方程称为激进方程


