9.5: 除以平方根
- Page ID
- 204331
在本节结束时,您将能够:
- 除以平方根
- 合理化单项分母
- 合理化两项分母
除以平方根
我们知道,我们可以通过移除分子和分母共有的因子来简化分数。 当我们在分子中有一个带有平方根的分数时,我们首先简化平方根。 然后我们可以寻找共同的因素。
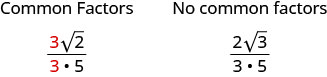
简化:\(\frac{\sqrt{54}}{6}\)
- 回答
-
\(\frac{\sqrt{54}}{6}\) 简化激进。 \(\frac{\sqrt{9}·\sqrt{6}}{6}\) 简化。 \(\frac{3\sqrt{6}}{6}\) 移除常见因素。 \(\frac{3\sqrt{6}}{3·2}\) 简化。 \(\frac{\sqrt{6}}{2}\)
简化:\(\frac{\sqrt{32}}{8}\)。
- 回答
-
\(\frac{\sqrt{2}}{2}\)
简化:\(\frac{\sqrt{75}}{15}\)。
- 回答
-
\(\frac{\sqrt{3}}{3}\)
简化:\(\frac{6−\sqrt{24}}{12}\)。
- 回答
-
\(\frac{6−\sqrt{24}}{12}\) 简化激进。 \(\frac{6−\sqrt{4}·\sqrt{6}}{12}\) 简化。 \(\frac{6−2\sqrt{6}}{12}\) 将分子中的公因子分解。 \(\frac{2(3−\sqrt{6})}{12}\) 移除常见因素。 \(\frac{2(3−\sqrt{6})}{2·6}\) 简化。 \(\frac{3−\sqrt{6}}{6}\)
简化:\(\frac{8−\sqrt{40}}{10}\)。
- 回答
-
\(\frac{4−\sqrt{10}}{5}\)
简化:\(\frac{10−\sqrt{75}}{20}\)。
- 回答
-
\(\frac{5−\sqrt{3}}{4}\)
我们使用了平方根的商属性来简化分数的平方根。 平方根的商属性说
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\),\(b \ne 0\)。
有时我们需要 “反向” 使用平方根的商属性来简化具有平方根的分数。
\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\),\(b \ne 0\)。
我们将重写平方根的商属性,这样我们就可以一起看待两种情况。 请记住:我们假设所有变量都大于或等于零,因此它们的平方根是实数。
如果 a, b 是非负实数\(b \ne 0\),那么
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)和\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
当我们开头的分数是两个平方根的商时,我们将 “反向” 使用平方根的商属性,并且两个 radicand 都不是完美的正方形。 当我们用单平方根写分数时,我们可能会在分子和分母中找到共同的因子。
简化:\(\frac{\sqrt{27}}{\sqrt{75}}\)
- 回答
-
\(\frac{\sqrt{27}}{\sqrt{75}}\) 两个 radicand 都不是完美的正方形,因此请使用平方根的商属性进行重写。 \(\sqrt{\frac{27}{75}}\) 删除分子和分母中的常见因子。 \(\sqrt{\frac{9}{25}}\) 简化。 \(\frac{3}{5}\)
简化:\(\frac{\sqrt{48}}{\sqrt{108}}\)
- 回答
-
\(\frac{2}{3}\)
简化:\(\frac{\sqrt{96}}{\sqrt{54}}\)
- 回答
-
\(\frac{4}{3}\)
当我们在基数中有指数的变量时\(\frac{a^m}{a^n}=a^{m−n}\),我们将使用指数的商属性。
简化:\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)
- 回答
-
\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\) 两个 radicand 都不是完美的正方形,因此请使用平方根的商属性进行重写。 \(\sqrt{\frac{6y^5}{2y}}\) 删除分子和分母中的常见因子。 \(\sqrt{3y^4}\) 简化。 \(y^2\sqrt{3}\)
简化:\(\frac{\sqrt{12r^3}}{\sqrt{6r}}\)。
- 回答
-
\(r\sqrt{2}\)
简化:\(\frac{\sqrt{14p^9}}{\sqrt{2p^5}}\)
- 回答
-
\(p^2\sqrt{7}\)
简化:\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)
- 回答
-
\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\) 使用平方根的商属性重写。 \(\sqrt{\frac{72x^3}{162x}}\) 移除常见因素。 \(\sqrt{\frac{18·4·x^2·x}{18·9·x}}\) 简化。 \(\sqrt{\frac{4x^2}{9}}\) 简化激进。 \(\frac{2x}{3}\)
简化:\(\frac{\sqrt{50s^3}}{\sqrt{128s}}\)。
- 回答
-
\(\frac{5s}{8}\)
简化:\(\frac{\sqrt{75q^5}}{\sqrt{108q}}\)。
- 回答
-
\(\frac{5q^2}{6}\)
简化:\(\frac{\sqrt{147ab^8}}{\sqrt{3a^3b^4}}\)。
- 回答
-
\(\frac{\sqrt{147ab^8}}{\sqrt{3a^{3}b^{4}}}\) 使用平方根的商属性重写。 \(\sqrt{\frac{147ab^8}{3a^{3}b^{4}}}\) 移除常见因素。 \ (\ sqrt {\ frac {49b^4} {a^2}}\ 简化激进。 \(\frac{7b^2}{a}\)
简化:\(\frac{\sqrt{162x^{10}y^{2}}}{\sqrt{2x^6y^6}}\)。
- 回答
-
\(\frac{9x^2}{y^2}\)
简化:\(\frac{\sqrt{300m^{3}n^{7}}}{\sqrt{3m^{5}n}}\)。
- 回答
-
\(\frac{10n^3}{m}\)
合理化单项分母
在计算器成为日常生活工具之前,使用平方根表来计算平方根的近似值。 该@@ 图显示了平方和平方根表的一部分。 在此表中,平方根近似于小数点后五位。
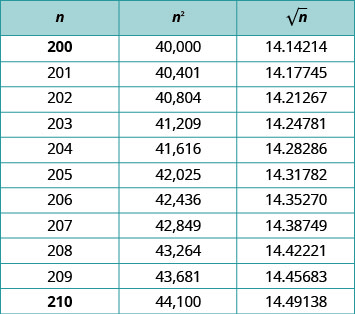
如果有人需要用分母中的平方根来近似分数,那就意味着用五位小数除数进行长除法。 这是一个非常繁琐的过程。
为此,制定了一个名为 “分母合理化” 的流程。 分母中有激进的分数被转换为分母为整数的等效分数。 这个过程至今仍在使用,在其他数学领域也很有用。
将分母中有激进的分数转换为分母为整数的等效分数的过程称为合理化分母。
不是完美正方形的数字的平方根是非理性数。 当我们对分母进行合理化时,我们会写一个等效的分数,分母中有一个有理数。
让我们来看一个数字示例。
\[\begin{array}{ll} {\text{Suppose we need an approximate value for the fraction.}}&{\frac{1}{\sqrt{2}}}\\ {\text{A five decimal place approximation to} \sqrt{2} \text{is} 1.41421}&{\frac{1}{1.41421}}\\ {\text{Without a calculator, would you want to do this division?}}&{1.41421) \overline{1.0}}\\ \nonumber \end{array}\]
但是我们可以通过将分子和分母\(\frac{1}{\sqrt{2}}\)乘以来找到等效于的分数\(\sqrt{2}\)。
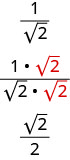
现在,如果我们需要一个近似值,我们就除以\(2) \overline{1.41421}\)。 这要容易得多。
尽管我们几乎到处都有计算器,但仍必须合理化分母中带有激进分母的分数。 如果分母包含平方根,则不视为简化。
同样,如果 radicand 包含分数,则不认为平方根是简化的。
如果有,则认为平方根是简化的
- 基数中没有完美平方因子
- 基数中没有分数
- 分数的分母中没有平方根
为了合理化分母,我们使用以下属性\((\sqrt{a})^2=a\). If we square an irrational square root, we get a rational number.
在下一个示例中,我们将使用此属性来合理化分母。
简化:\(\frac{4}{\sqrt{3}}\)。
- 回答
-
要从分母中移除平方根,我们将其自身相乘。 为了保持分数相等,我们将分子和分母乘以相同的因子。
\(\frac{4}{\sqrt{3}}\)
将分子和分母乘以\(\sqrt{3}\)\(\frac{4·\sqrt{3}}{\sqrt{3}·\sqrt{3}}\) 简化。 \(\frac{4\sqrt{3}}{3}\)
简化:\(\frac{5}{\sqrt{3}}\)。
- 回答
-
\(\frac{5\sqrt{3}}{3}\)
简化:\(\frac{6}{\sqrt{5}}\)。
- 回答
-
\(\frac{6\sqrt{5}}{5}\)
简化:\(−\frac{8}{3\sqrt{6}}\)
- 回答
-
要从分母中移除平方根,我们将其自身相乘。 为了保持分数相等,我们将分子和分母乘以\(\sqrt{6}\)。
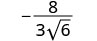
将分子和分母都乘以\(\sqrt{6}\)。 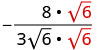
简化。 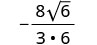
移除常见因素。 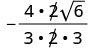
简化。 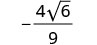
简化:\(\frac{5}{2\sqrt{5}}\)。
- 回答
-
\(\frac{\sqrt{5}}{2}\)
简化:\(−\frac{9}{4\sqrt{3}}\)。
- 回答
-
\(−\frac{3\sqrt{3}}{4}\)
在合理化分母之前,务必先简化分母中的激进。 这样,数字就会变得更小,更易于处理。
简化:\(\sqrt{\frac{5}{12}}\)。
- 回答
-
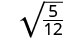
分数不是完美的正方形,因此请使用
商属性进行重写。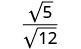
简化分母。 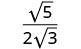
合理化分母。 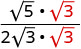
简化。 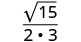
简化。 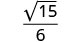
简化:\(\sqrt{\frac{7}{18}}\)。
- 回答
-
\(\frac{\sqrt{14}}{6}\)
简化:\(\sqrt{\frac{3}{32}}\)。
- 回答
-
\(\frac{\sqrt{6}}{8}\)
简化:\(\sqrt{\frac{11}{28}}\)
- 回答
-
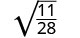
使用 Quotient 属性重写。 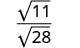
简化分母。 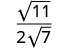
合理化分母。 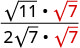
简化。 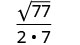
简化。 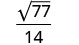
简化:\(\sqrt{\frac{3}{27}}\)。
- 回答
-
\(\frac{1}{3}\)
简化:\(\sqrt{\frac{10}{50}}\)
- 回答
-
\(\frac{\sqrt{5}}{5}\)
合理化两项分母
当分数的分母是平方根的总和或差时,我们使用共轭乘积模式来合理化分母。
\[\begin{array}{ll} {(a−b)(a+b)}&{(2−\sqrt{5})(2+\sqrt{5})}\\ {a^2−b^2}&{2^2−(\sqrt{5})^2}\\ {}&{4−5}\\ {}&{−1}\\ \nonumber \end{array}\]
当我们将包含平方根的二项式乘以其共轭物时,乘积没有平方根。
简化:\(\frac{4}{4+\sqrt{2}}\)。
- 回答
-
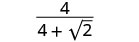
将分子和分母乘以分母的共轭。 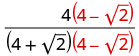
将分母中的共轭物相乘。 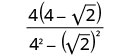
简化分母。 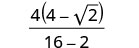
简化分母。 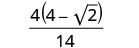
从分子和分母中移除常见因子。 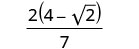
我们以因子形式保留分子,以便在简化分母后更容易寻找常见因子。
简化:\(\frac{2}{2+\sqrt{3}}\)。
- 回答
-
\(\frac{2(2−\sqrt{3})}{1}\)
简化:\(\frac{5}{5+\sqrt{3}}\)。
- 回答
-
\(\frac{5(5−\sqrt{3})}{22}\)
简化:\(\frac{5}{2−\sqrt{3}}\)。
- 回答
-
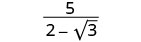
将分子和分母乘以分母的共轭。 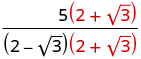
将分母中的共轭物相乘。 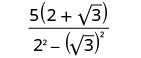
简化分母。 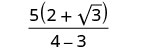
简化分母。 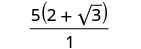
简化。 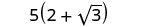
简化:\(\frac{3}{1−\sqrt{5}}\)。
- 回答
-
\(−\frac{3(1+\sqrt{5})}{4}\)
简化:\(\frac{2}{4−\sqrt{6}}\)。
- 回答
-
\(\frac{4+\sqrt{6}}{5}\)
简化:\(\frac{\sqrt{3}}{\sqrt{u}−\sqrt{6}}\)。
- 回答
-
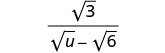
将分子和分母乘以分母的共轭。 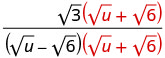
将分母中的共轭物相乘。 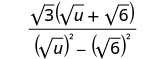
简化分母。 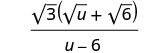
简化:\(\frac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\)。
- 回答
-
\(\frac{\sqrt{5}(\sqrt{x}−\sqrt{2})}{x−2}\)
简化:\(\frac{\sqrt{10}}{\sqrt{y}−\sqrt{3}}\)。
- 回答
-
\(\frac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y−3}\)
简化:\(\frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}−\sqrt{7}}\)。
- 回答
-
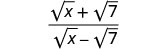
将分子和分母乘以分母的共轭。 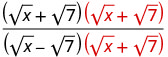
将分母中的共轭物相乘。 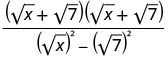
简化分母。 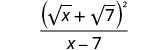
我们不对分子求平方。 在因子计算的形式中,我们可以看到没有常见的因子可以从分子和分母中移除。
简化:\(\frac{\sqrt{p}+\sqrt{2}}{\sqrt{p}−\sqrt{2}}\).
- 回答
-
\(\frac{(\sqrt{p}+\sqrt{2})^2}{p−2}\)
简化:\(\frac{\sqrt{q}−\sqrt{10}}{\sqrt{q}+\sqrt{10}}\)。
- 回答
-
\(\frac{(\sqrt{q}−\sqrt{10})^2}{q−10}\)
访问此在线资源,通过划分和合理化获得更多指导和练习。
- 分裂和合理化
关键概念
- 平方根的商特性
- 如果 a, b 是非负实数\(b \ne 0\),那么
\(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)和\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
- 如果 a, b 是非负实数\(b \ne 0\),那么
- 简化的平方根
如果有,则认为平方根是简化的- 在 radicand 中没有完美的平方因子
- 基数中没有分数
- 分数的分母中没有平方根
词汇表
- 合理化分母
- 将分母中有激进的分数转换为分母为整数的等效分数的过程称为合理化分母。


