9.4E:练习
- Page ID
- 204369
练习成就完美
乘以平方根
在以下练习中,进行简化。
- \(\sqrt{2}·\sqrt{8}\)
- \((3\sqrt{3})(2\sqrt{18})\)
- 回答
-
- \(44\)
- \(18\sqrt{6}\)
- \(\sqrt{6}·\sqrt{6}\)
- \((3\sqrt{2})(2\sqrt{32})\)
- \(\sqrt{7}·\sqrt{14}\)
- \((4\sqrt{8})(5\sqrt{8})\)
- 回答
-
- \(7\sqrt{2}\)
- 160
- \(\sqrt{6}·\sqrt{12}\)
- \((2\sqrt{5})(2\sqrt{10})\)
\((5\sqrt{2})(3\sqrt{6})\)
- 回答
-
\(30\sqrt{3}\)
\((2\sqrt{3})(4\sqrt{6})\)
\((−2\sqrt{3})(3\sqrt{18})\)
- 回答
-
\(−18\sqrt{6}\)
\((−4\sqrt{5})(5\sqrt{10})\)
\((5\sqrt{6})(−\sqrt{12})\)
- 回答
-
\(−30\sqrt{2}\)
\((6\sqrt{2})(−\sqrt{10})\)
\((−2\sqrt{7})(−2\sqrt{14})\)
- 回答
-
\(28\sqrt{2}\)
\((−2\sqrt{11})(−4\sqrt{22})\)
- \((\sqrt{15y})(\sqrt{5y^3})\)
- \((\sqrt{2n^2})(\sqrt{18n^3})\)
- 回答
-
- \(5y^2\sqrt{3}\)
- \(6n^2\sqrt{n}\)
- \((\sqrt{14x^3})(\sqrt{7x^3})\)
- \((\sqrt{3q^2})(\sqrt{48q^3})\)
- \((\sqrt{16y^2})(\sqrt{8y^4})\)
- \((\sqrt{11s^6})(\sqrt{11s})\)
- 回答
-
- \(8y^3\sqrt{2}\)
- \(11s^3\sqrt{s}\)
ⓐ\((\sqrt{8x^3})(\sqrt{3x})\)
ⓑ\((\sqrt{7r})(\sqrt{7r^8})\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
- 回答
-
\(40b^2\sqrt{3}\)
\((\sqrt{38c^5})(\sqrt{26c^3})\)
\((6\sqrt{3d^3})(4\sqrt{12d^5})\)
- 回答
-
\(144d^4\)
\((2\sqrt{5b^3})(4\sqrt{15b})\)
\((2\sqrt{5d^6})(3\sqrt{20d^2})\)
- 回答
-
\(60d^4\)
\((−2\sqrt{7z^3})(3\sqrt{14z^8})\)
\((4\sqrt{2k^5})(−3\sqrt{32k^6})\)
- 回答
-
\(−96k^5\sqrt{k}\)
- \((\sqrt{7})^2\)
- \((−\sqrt{15})^2\)
- \((\sqrt{11})^2\)
- \((−\sqrt{21})^2\)
- 回答
-
- 11
- 21
- \((\sqrt{19})^2\)
- \((−\sqrt{5})^2\)
- \((\sqrt{23})^2\)
- \((−\sqrt{3})^2\)
- 回答
-
- 23
- 3
- \((4\sqrt{11})(−3\sqrt{11})\)
- \((5\sqrt{3})^2\)
- \((2\sqrt{13})(−9\sqrt{13})\)
- \((6\sqrt{5})^2\)
- 回答
-
- −234
- 180
- \((−3\sqrt{12})(−2\sqrt{6})\)
- \( (−4\sqrt{10})^2\)
- \((−7\sqrt{5})(−3\sqrt{10})\)
- \( (−2\sqrt{14})^2\)
- 回答
-
- \(105\sqrt{2}\)
- 56
使用多项式乘法乘以平方根
在以下练习中,进行简化。
- \(3(4−\sqrt{3})\)
- \(\sqrt{2}(4−\sqrt{6})\)
- \(4(6−\sqrt{11})\)
- \(\sqrt{2}(5−\sqrt{12})\)
- 回答
-
- \(24−4\sqrt{11}\)
- \(5\sqrt{2}−2\sqrt{6}\)
- \(5(3−\sqrt{7})\)
- \(\sqrt{3}(4−\sqrt{15})\)
- \(7(−2−\sqrt{11})\)
- \(\sqrt{7}(6−\sqrt{14})\)
- 回答
-
- \(−14−7\sqrt{11}\)
- \(6\sqrt{7}−7\sqrt{2}\)
- \(\sqrt{7}(5+2\sqrt{7})\)
- \(\sqrt{5}(\sqrt{10}+\sqrt{18})\)
- \(\sqrt{11}(8+4\sqrt{11})\)
- \(\sqrt{3}(\sqrt{12}+\sqrt{27})\)
- 回答
-
- \(44+8\sqrt{11}\)
- 15
- \(\sqrt{11}(−3+4\sqrt{1})\)
- \(\sqrt{3}(\sqrt{15}−\sqrt{18})\)
- \(\sqrt{2}(−5+9\sqrt{2})\)
- \(\sqrt{7}(\sqrt{3}−\sqrt{21})\)
- 回答
-
- \(18−5\sqrt{2}\)
- \(\sqrt{21}−7\sqrt{3}\)
\((8+\sqrt{3})(2−\sqrt{3})\)
\((7+\sqrt{3})(9−\sqrt{3})\)
- 回答
-
\(60+2\sqrt{3}\)
\((8−\sqrt{2})(3+\sqrt{2})\)
\((9−\sqrt{2})(6+\sqrt{2})\)
- 回答
-
\(52+3\sqrt{2}\)
\((3−\sqrt{7})(5−\sqrt{7})\)
\((5−\sqrt{7})(4−\sqrt{7})\)
- 回答
-
\(27−9\sqrt{7}\)
\((1+3\sqrt{10})(5−2\sqrt{10})\)
\((7−2\sqrt{5})(4+9\sqrt{5})\)
- 回答
-
\(−62+55\sqrt{5}\)
\((\sqrt{3}+\sqrt{10})(\sqrt{3}+2\sqrt{10})\)
\((\sqrt{11}+\sqrt{5})(\sqrt{11}+6\sqrt{5})\)
- 回答
-
\(41+7\sqrt{55}\)
\((2\sqrt{7}−5\sqrt{11})(4\sqrt{7}+9\sqrt{11})\)
\((4\sqrt{6}+7\sqrt{13})(8\sqrt{6}−3\sqrt{13})\)
- 回答
-
\(−81+44\sqrt{78}\)
\((5−\sqrt{u})(3+\sqrt{u})\)
\((9−\sqrt{w})(2+\sqrt{w})\)
- 回答
-
\(18+7\sqrt{w}\)
\((7+2\sqrt{m})(4+9\sqrt{m})\)
\((6+5\sqrt{n})(11+3\sqrt{n})\)
- 回答
-
\(66+73\sqrt{n}+15n\)
- \((3+\sqrt{5})^2\)
- \((2−5\sqrt{3})^2\)
- \((4+\sqrt{11})^2\)
- \((3−2\sqrt{5})^2\)
- 回答
-
- \(27+8\sqrt{11}\)
- \(29−12\sqrt{5}\)
- \((9−\sqrt{6})^2\)
- \((10+3\sqrt{7})^2\)
- \((5−\sqrt{10})^2\)
- \((8+3\sqrt{2})^2\)
- 回答
-
- \(35−10\sqrt{10}\)
- \(82+48\sqrt{2}\)
\((3−\sqrt{5})(3+\sqrt{5})\)
\((10−\sqrt{3})(10+\sqrt{3})\)
- 回答
-
97
\((4+\sqrt{2})(4−\sqrt{2})\)
\((7+\sqrt{10})(7−\sqrt{10})\)
- 回答
-
39
\((4+9\sqrt{3})(4−9\sqrt{3})\)
\((1+8\sqrt{2})(1−8\sqrt{2})\)
- 回答
-
−127
\((12−5\sqrt{5})(12+5\sqrt{5})\)
\((9−4\sqrt{3})(9+4\sqrt{3})\)
- 回答
-
33
混合练习
在以下练习中,进行简化。
\(\sqrt{3}·\sqrt{21}\)
\((4\sqrt{6})(−\sqrt{18})\)
- 回答
-
\(−24\sqrt{3}\)
\((−5+\sqrt{7})(6+\sqrt{21})\)
\((−5\sqrt{7})(6\sqrt{21})\)
- 回答
-
\(−210\sqrt{3}\)
\((−4\sqrt{2})(2\sqrt{18})\)
\((\sqrt{35y^3})(\sqrt{7y^3})\)
- 回答
-
\(7y^3\sqrt{5}\)
\((4\sqrt{12x^5})(2\sqrt{6x^3})\)
\((\sqrt{29})^2\)
- 回答
-
29
\((−4\sqrt{17})(−3\sqrt{17})\)
\((−4+\sqrt{17})(−3+\sqrt{17})\)
- 回答
-
\(29−7\sqrt{17}\)
日常数学
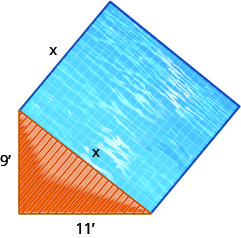
园丁想在三角形甲板旁边放一个方形反射池,如下所示。 三角形甲板是一个直角三角形,腿长 9 英尺和 11 英尺,水池将与斜边相邻。
- 使用毕达哥拉斯定理找出水池一侧的长度。 将答案四舍五入到最接近的十分之一英尺。
- 找到游泳池的确切区域。
一位艺术家想要制作一座小纪念碑,其形状为方形底座,顶部为直角三角形,如下所示。 方形底部将与三角形的一条腿相邻。 三角形的另一条腿长 2 英尺,斜边将为 5 英尺。
- 使用毕达哥拉斯定理找出正方形底边的长度。 将答案四舍五入到最接近的十分之一英尺。
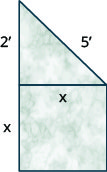
- 找到正方形底座表面的确切面积。
- 回答
-
- 4.6 英尺
- 21 平方英尺
将用石头边框建造一个方形花园。 如果只有\(3+\sqrt{10}\)几英尺的石头可用,\((3+\sqrt{10})^2\)请简化以确定最大的此类花园的面积。
将建造一个花园,使其包含两个方形部分,一个部分有边长\(\sqrt{5}+\sqrt{6}\)码,另一个部分有边长\(\sqrt{2}+\sqrt{3}\)码。 简化\((\sqrt{5}+\sqrt{6})(\sqrt{2}+\sqrt{3})\)以确定花园的总面积。
假设在前面的练习中,将向花园添加第三个部分。 第三部分的宽度为英\(\sqrt{432}\)尺。 写一个表达式,给出花园的总面积。
写作练习
- 解释为什么\((−\sqrt{n})^2\)总是积极的,因为\(n \ge 0\)。
- 解释为什么\(−(\sqrt{n})^2\)总是负面的,对于\(n \ge 0\)。
- 回答
-
- 当求负数平方时,它变成正数
- 由于负数未包含在括号中,因此它不是平方,并且仍然是负数
使用二项式方形图案进行简化\((3+\sqrt{2})^2\)。 解释你的所有步骤。
自检
ⓐ 完成练习后,使用这份清单来评估你对本节目标的掌握程度。
ⓑ 在 1-10 的等级中,根据你在清单上的回复,你会如何评价你对本节的掌握程度? 你怎么能改善这个?


