9.4: 乘以平方根
- Page ID
- 204350
在本节结束时,您将能够:
- 乘以平方根
- 使用多项式乘法将平方根相乘
乘以平方根
我们使用平方根的乘积属性通过移除完美平方因子来简化平方根。 平方根的乘积特性说
\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]
我们可以 “反向” 使用平方根的乘积属性来乘以平方根。
\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]
请记住,我们假设所有变量都大于或等于零。
我们将重写平方根的乘积属性,这样我们就可以一起看清两种情况。
如果 a, b 是非负实数,那么
\(\sqrt{ab}=\sqrt{a}·\sqrt{b}\)和\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\)。
这样我们就可以乘以\(\sqrt{3}·\sqrt{5}\) in this way:
\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]
有时产品会给我们一个完美的正方形:
\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]
即使乘积不是完美的正方形,我们也必须寻找完美平方因子并尽可能简化基数。
将自由基与系数相乘很像将变量与系数相乘。 要乘以 4x·3y,我们将系数乘在一起,然后乘以变量。 结果是 12xy。 在做这些例子时,请记住这一点。
简化:
- \(\sqrt{2}·\sqrt{6}\)
- \((4\sqrt{3})(2\sqrt{12})\)。
- 回答
-
1。 \(\sqrt{2}·\sqrt{6}\) 使用产品属性乘以。 \(\sqrt{12}\) 简化激进。 \(\sqrt{4}·\sqrt{3}\) 简化。 \(2\sqrt{3}\) 2。 \((4\sqrt{3})(2\sqrt{12})\) 使用产品属性乘以。 \(8\sqrt{36}\) 简化激进。 \(8·6\) 简化。 \(48\)
简化:
- \(\sqrt{3}·\sqrt{6}\)
- \((2\sqrt{6})(3\sqrt{12})\)。
- 回答
-
- \(3\sqrt{2}\)
- \(36\sqrt{2}\)
简化:
- \(\sqrt{5}·\sqrt{10}\)
- \((6\sqrt{3})(5\sqrt{6})\)
- 回答
-
- \(5\sqrt{2}\)
- \(90\sqrt{2}\)
简化:\((6\sqrt{2})(3\sqrt{10})\)
- 回答
-
\((6\sqrt{2})(3\sqrt{10})\) 使用产品属性乘以。 \(18\sqrt{20}\) 简化激进。 \(18\sqrt{4}·\sqrt{5}\) 简化。 \(18·2·\sqrt{5}\) \(36\sqrt{5}\)
简化:\((3\sqrt{2})(2\sqrt{30})\)
- 回答
-
\(12\sqrt{15}\)
简化:\((3\sqrt{3})(3\sqrt{6})\)。
- 回答
-
\(27\sqrt{2}\)
当我们必须乘以平方根时,我们首先找到乘积,然后去除任何完美的平方因子。
简化:
- \((\sqrt{8x^3})(\sqrt{3x})\)
- \((\sqrt{20y^2})(\sqrt{5y^3})\)
- 回答
-
1。 \((\sqrt{8x^3})(\sqrt{3x})\) 使用产品属性乘以。 \(\sqrt{24x^4}\) 简化激进。 \(\sqrt{4x^4}·\sqrt{6}\) 简化。 \(2x^2\sqrt{6}\) 2。 \((\sqrt{20y^2})(\sqrt{5y^3})\) 使用产品属性乘以。 \(\sqrt{100y^5}\) 简化激进。 \(10y^2\sqrt{y}\)
简化:
- \((\sqrt{6x^3})(\sqrt{3x})\)
- \((\sqrt{2y^3})(\sqrt{50y^2})\)。
- 回答
-
- \(3x^2\sqrt{2}\)
- \(10y^2\sqrt{y}\)
简化:
- \((\sqrt{6x^5})(\sqrt{2x})\)
- \((\sqrt{12y^2})(\sqrt{3y^5})\)
- 回答
-
- \(2x^3\sqrt{3}\)
- \(6y^2\sqrt{y}\)
简化:\((10\sqrt{6p^3})(3\sqrt{18p})\)
- 回答
-
\((10\sqrt{6p^3})(3\sqrt{18p})\) 乘以。 \(30\sqrt{108p^4}\) 简化激进。 \(30\sqrt{36p^4}·\sqrt{3}\) \(30·6p^2·\sqrt{3}\) \(180p^2\sqrt{3}\)
简化:\((\sqrt{62x^2})(8\sqrt{45x^4})\)
- 回答
-
\(144x^3\sqrt{10}\)
简化:\((2\sqrt{6y^4})(12\sqrt{30y})\)。
- 回答
-
\(144y^2\sqrt{5y}\)
简化:
- \((\sqrt{2})^2\)
- \((−\sqrt{11})^2\)。
- 回答
-
1。 \((\sqrt{2})^2\) 重写为产品。 \((\sqrt{2})(\sqrt{2})\) 乘以。 \(\sqrt{4}\) 简化。 2 2。 \((−\sqrt{11})^2\) 重写为产品。 \((−\sqrt{11})(−\sqrt{11})\) 乘以。 \(\sqrt{121}\) 简化。 11
简化:
- \((\sqrt{12})^2\)
- \((−\sqrt{15})^2\)。
- 回答
-
- 12
- 15
简化:
- \((\sqrt{16})^2\)
- \((−\sqrt{20})^2\)。
- 回答
-
- 16
- 20
前一个示例的结果将我们引导到这个属性。
如果 a 是非负实数,则
\((\sqrt{a})^2=a\)
意识到平方和取平方根是 “相反的” 运算,我们可以简化\((\sqrt{2})^2\)并立即得出 2。 当我们在下一个示例(a)部分中将两者相乘时,等于平方根。
简化:
- \((2\sqrt{3})(8\sqrt{3})\)
- \((3\sqrt{6})^2\)。
- 回答
-
1。 \((2\sqrt{3})(8\sqrt{3})\) 乘以。 记住,\((\sqrt{3}^2)\) 16·3 简化。 48 2。 \((3\sqrt{6})^2\) 乘以。 9·6 简化。 54
简化:
- \((6\sqrt{11})(5\sqrt{11})\)
- \((5\sqrt{8})^2\)。
- 回答
-
- 330
- 200
简化:
- \((3\sqrt{7})(10\sqrt{7})\)
- \((−4\sqrt{6})^2\)。
- 回答
-
- 210
- 96
使用多项式乘法乘以平方根
在接下来的几个示例中,我们将使用分布属性将表达式与平方根相乘。
我们将首先分布,然后尽可能简化平方根。
简化:
- \(3(5−\sqrt{2})\)
- \(\sqrt{2}(4−\sqrt{10})\)。
- 回答
-
1。 \(3(5−\sqrt{2})\) 分发。 \(15−3\sqrt{2})\) 2。 \(\sqrt{2}(4−\sqrt{10})\) 分发。 \(4\sqrt{2}−\sqrt{20}\) 简化。 \(4\sqrt{2}−2\sqrt{5}\)
简化:
- \(2(3−\sqrt{5})\)
- \(\sqrt{3}(2−\sqrt{18})\)。
- 回答
-
- \(6−2\sqrt{5}\)
- \(2\sqrt{3}−3\sqrt{6}\)
简化:
- \(6(2+\sqrt{6})\)
- \(\sqrt{7}(1+\sqrt{14})\)。
- 回答
-
- \(12+\sqrt{6}\)
- \(\sqrt{7}+7\sqrt{2}\)
简化:
- \(\sqrt{5}(7+2\sqrt{5})\)
- \(\sqrt{6}(\sqrt{2}+\sqrt{18})\)。
- 回答
-
1。 \(\sqrt{5}(7+2\sqrt{5})\) 分发。 \(7\sqrt{5}+2·5\) 简化。 \(7\sqrt{5}+10\) \(10+7\sqrt{5}\) 2。 \(\sqrt{6}(\sqrt{2}+\sqrt{18})\) 乘以。 \(\sqrt{12}+\sqrt{108}\) 简化。 \((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\) \(2\sqrt{3}+6\sqrt{3}\) 像激进分子一样结合。 \(8\sqrt{3}\)
简化:
- \(\sqrt{6}(1+3\sqrt{6})\)
- \(\sqrt{12}(\sqrt{3}+\sqrt{24})\)
- 回答
-
- \(18+\sqrt{6}\)
- \(6+12\sqrt{2}\)
简化:
- \(\sqrt{8}(2−5\sqrt{8})\)
- \(\sqrt{14}(\sqrt{2}+\sqrt{42})\)
- 回答
-
- \(−40+4\sqrt{2}\)
- \(2\sqrt{7}+14\sqrt{3}\)
当我们处理多项式时,我们将二项式乘以二项式。 请记住,在我们合并任何类似术语之前,这给了我们四种产品。 为了确保获得所有四种产品,我们组织了工作——通常采用FOIL方法。
简化:\((2+\sqrt{3})(4−\sqrt{3})\)
- 回答
-
\((2+\sqrt{3})(4−\sqrt{3})\) 乘以。 \(8−2\sqrt{3}+4\sqrt{3}−3\) 将相似的术语组合在一起。 \(5+2\sqrt{3}\)
简化:\((1+\sqrt{6})(3−\sqrt{6})\)。
- 回答
-
\(−3+2\sqrt{6}\)
简化:\((4−\sqrt{10})(2+\sqrt{10})\)。
- 回答
-
\(−2+2\sqrt{10}\)
简化:\((3−2\sqrt{7})(4−2\sqrt{7})\)。
- 回答
-
\((3−2\sqrt{7})(4−2\sqrt{7})\) 乘以。 \(12−6\sqrt{7}−8\sqrt{7}+4·7\) 简化。 \(12−6\sqrt{7}−8\sqrt{7}+28\) 将相似的术语组合在一起。 \(40−14\sqrt{7}\)
简化:\((6−3\sqrt{7})(3+4\sqrt{7})\)。
- 回答
-
\(−66+15\sqrt{7}\)
简化:\((2−3\sqrt{11})(4−\sqrt{11})\)
- 回答
-
\(41+14\sqrt{11}\)
简化:\((3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\)。
- 回答
-
\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\) 乘以。 \(3·2+12\sqrt{10}−\sqrt{10}−4·5\) 简化。 \(6+12\sqrt{10}−\sqrt{10}−20\) 将相似的术语组合在一起。 \(−14+11\sqrt{10}\)
简化:\((5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})\)
- 回答
-
\(1+9\sqrt{21}\)
简化:\((\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})\)
- 回答
-
\(−12−20\sqrt{3}\)
简化:\((4−2\sqrt{x})(1+3\sqrt{x})\)。
- 回答
-
\((4−2\sqrt{x})(1+3\sqrt{x})\)。 乘以。 \(4+12\sqrt{x}−2\sqrt{x}−6x\) 将相似的术语组合在一起。 \(4+10\sqrt{x}−6x\)
简化:\((6−5\sqrt{m})(2+3\sqrt{m})\)。
- 回答
-
\(12+8\sqrt{m}−15m\)
简化:\((10+3\sqrt{n})(1−5\sqrt{n})\)
- 回答
-
\(10−47\sqrt{n}−15n\)
请注意,当我们之前乘以二项式时,一些特殊产品使我们的工作变得更容易。 当我们乘以平方根时也是如此。 我们使用的特殊产品配方如下所示。
\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]
我们将在接下来的几个示例中使用特殊的产品配方。 我们将从二项式平方公式开始。
简化:
- \((2+\sqrt{3})^2\)
- \((4−2\sqrt{5})^2\)。
- 回答
-
求二项式求方时务必包含 2ab 项。
1。
2。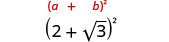
使用二项式正方形图案进行乘法。 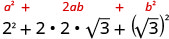
简化。 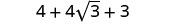
将相似的术语组合在一起。 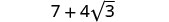
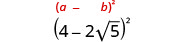
使用二项式正方形图案进行乘法。 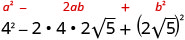
简化。 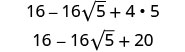
将相似的术语组合在一起。 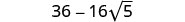
简化:
- \((10+\sqrt{2})^2\)
- \((1+3\sqrt{6})^2\)。
- 回答
-
- \(102+20\sqrt{2}\)
- \(55+6\sqrt{6}\)
简化:
- \((6-\sqrt{5})^2\)
- \((9-2\sqrt{10})^2\)。
- 回答
-
- \(41-12\sqrt{5}\)
- \(121-36\sqrt{10}\)
简化:\((1+3\sqrt{x})^2\)。
- 回答
-
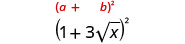
使用二项式正方形图案进行乘法。 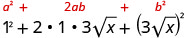
简化。 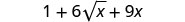
简化:\((2+5\sqrt{m})^2\)。
- 回答
-
\(4+20\sqrt{m}+25m\)
简化:\((3−4\sqrt{n})^2\)。
- 回答
-
\(9−24\sqrt{n}+16n\)
在接下来的两个例子中,我们将找到共轭物的乘积。
简化:\((4−\sqrt{2})(4+\sqrt{2})\)。
- 回答
-
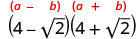
使用二项式正方形图案进行乘法。 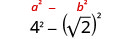
简化。 
简化:\((2−\sqrt{3})(2+\sqrt{3})\)
- 回答
-
1
简化:\((1+\sqrt{5})(1−\sqrt{5})\)
- 回答
-
−4
简化:\((5−2\sqrt{3})(5+2\sqrt{3})\)
- 回答
-
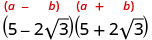
使用二项式正方形图案进行乘法。 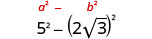
简化。 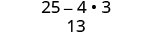
简化:\((3−2\sqrt{5})(3+2\sqrt{5})\)。
- 回答
-
−11
简化:\((4+5\sqrt{7})(4−5\sqrt{7})\)。
- 回答
-
−159
访问这些在线资源以获取更多指导和使用乘法平方根进行练习。
- 产品特性
- 用平方根乘以二项式
关键概念
- 平方根的乘积属性如果 a, b 是非负实数,那么
\(\sqrt{ab}=\sqrt{a·b}\)和\(\sqrt{a}·\sqrt{b}=\sqrt{ab}\)
- 用于乘以二项@@ 式和共轭物的特殊公式:
\[\begin{array}{ll} {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2 }&{}\\ \nonumber \end{array}\]
- FOIL 方法可用于乘以含有自由基的二项式。


