8.9:使用直接变异和逆变量
- Page ID
- 204748
在本节结束时,您将能够:
- 解决直接变异问题
- 解决逆变问题
在开始之前,请参加这个准备测验。
如果您遗漏了问题,请返回列出的部分并查看材料。
- 找出 −8 的乘法逆数
如果你错过了这个问题,请查看练习 1.10.13。 - 求解 n: 45=20n
如果你错过了这个问题,请查看练习 2.2.1。 - 评估\(5x^2\)何时 x=10
如果你错过了这个问题,请查看练习 1.3.25。
当两个量按比例关联时,我们说它们彼此成正比。 表达这种关系的另一种方法是讨论两个量的变化。 在本节中,我们将讨论直接变异和逆变异。
解决直接变异问题
Lindsay 在工作时每小时可获得 15 美元的报酬。 如果我们假设我们是她的工资,h 是她的工作时数,我们可以用方程式来模拟这种情况
s=15h
Lindsay 的薪水是常数 15 和她工作时数的乘积。 我们说林赛的薪水与她的工作时数直接不同。 如果一个变量是常量的乘积而另一个变量是直接变化。
对于任意两个变量 x 和 y,y 与 x 直接变化
y=kx,哪里\(n \ne 0\)
在使用直接变异的应用程序中,通常我们会知道一对变量的值,并被要求找到与 x 和 y 相关的方程。 然后我们可以使用该方程为 x 的其他值找出 y 的值。
如何解决直接变异问题
如果 y 与 x 直接变化,当 x=8 时 y=20,则找出与 x 和 y 相关的方程。
- 回答
-
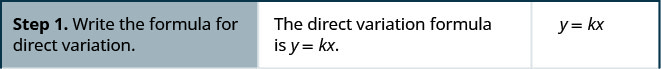



如果 y 直接变化为 x 和 y=3,则当 x=10 时,求出与 x 和 y 相关的方程。
- 回答
-
\(y=\frac{3}{10}x\)
如果 y 直接变化为 x,当 x=4 时 y=12,则找出与 x 和 y 相关的方程。
- 回答
-
y=3x
我们将在下面列出步骤。
- 写出直接变异的公式。
- 用给定值代替变量。
- 求解变异常数。
- 写出与 x 和 y 相关的方程。
现在我们将解决一些直接变异的应用。
当拉乌尔在健身房的跑步机上跑步时,他消耗的卡路里数量 c 与他使用跑步机的分钟数直接不同。 他在跑步机 18 分钟时消耗了 315 卡路里的热量。
- 写出与 c 和 m 相关的方程。
- 如果他在跑步机上跑了 25 分钟,他会消耗多少卡路里?
- 回答
-
1。
卡路里数量,c 与分钟数直接变化,m,在跑步机上,当 m=18 时 c=315 写出直接变异的公式。 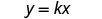
我们将使用 c 代替 y,用 mm 代替 x。 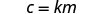
用给定值代替变量。 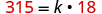
求解变异常数。 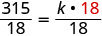
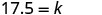
写出与 c 和 m 相关的方程。 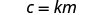
用变异常数代替。 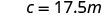
2。
当 m=25 时找到 c。
写出与 c 和 m 相关的方程。 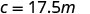
用给定值替换 m。 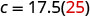
简化。 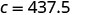
如果拉乌尔使用跑步机 25 分钟,他将消耗 437.5 卡路里的热量。
消耗的卡路里数量 c 直接随运动所花费的时间 t 而变化。 阿诺德在 65 分钟的锻炼中消耗了 312 卡路里的热量。
- 写出与 c 和 t 相关的方程。
- 如果他运动 90 分钟,他会消耗多少卡路里?
- 回答
-
- c=4.8t
- 432 卡路里
移动物体的行进距离 d 直接随时间变化,t,它会移动。 一列火车在 2 小时内行驶 100 英里
- 写出与 d 和 t 相关的方程。
- 它会在 5 小时内行驶多少英里?
- 回答
-
- d=50t
- 250 英里
在前面的示例中,问题中命名了变量 c 和 m。 通常情况并非如此。 我们必须在下一个示例中命名变量作为解决方案的一部分,就像我们在大多数应用问题中所做的那样。
尤妮丝的汽车消耗的加仑汽油数量与她行驶的里程数直接不同。 上周她开了469.8英里,用了14.5加仑的汽油。
- 写出将使用的加仑汽油数与行驶里程数相关的方程式。
- 如果尤妮丝开了 1000 英里,她的车会消耗多少加仑的汽油?
- 回答
-
1。
加仑的汽油数量直接随行驶里程数的变化而变化。 首先,我们将命名变量。 假设 g = 加仑汽油的数量。
m= 行驶的里程数。写出直接变异的公式。 
我们将使用 g 代替 y,用 m 代替 x。 
用给定值代替变量 
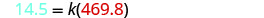
求解变异常数。 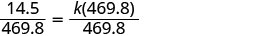
我们将四舍五入到最接近的千分之一。 
写出与 g 和 m 相关的方程。 
用变异常数代替。 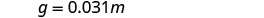
2。
当 m=1000 时找到 g。 写出与 g 和 m 相关的方程。 g=0.031m 用给定值替换 m。 g=0.031 (1000) 简化。 g=31 如果尤妮丝开了1000英里,她的汽车将消耗31加仑的汽油。 请注意,在本示例中,变异常数上的单位是加仑/英里。 在日常生活中,我们通常谈论英里/加仑。
布拉德旅行的距离直接因旅行所花费的时间而异。 布拉德在12小时内行驶了660英里
- 写出将行驶里程数与时间相关的方程式。
- 布拉德能在 4 小时内行驶多少英里?
- 回答
-
- m=55h
- 220 英里
液体的重量直接随其体积而变化。 重 24 磅的液体的体积为 4 加仑。
- 写出将重量与体积相关的方程式。
- 如果液体的体积为 13 加仑,它的重量是多少?
- 回答
-
- w=6v
- 78 磅
在某些情况下,一个变量直接与另一个变量的平方变化。 发生这种情况时,直接变异方程为\(y=kx^2\)。
梁承受的最大载荷直接随梁横截面对角线的平方而变化。 对角线为 4 英寸的光束将承受 75 磅的最大载荷。
- 写出将最大载荷与横截面相关的方程。
- 对角线为 8 英寸的梁所能承受的最大载荷是多少?
- 回答
-
1。
最大载荷直接随横截面对角线的平方而变化。 为变量命名。 假设 L = 最大负载。
c= 横截面的对角线写出直接变异的公式,其中 y 与 x 的平方直接变化。 
我们将使用 L 代替 y,用 c 代替 x。 
用给定值代替变量。 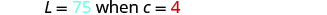

求解变异常数。 

写出与 L 和 c 相关的方程。 
用变异常数代替。 
2。
当 c=8 时找到 L。 写出与 L 和 c 相关的方程。 \(L=4.6875c^2\) 用给定值替换 c。 \(L=4.6875(8)^2\) 简化。 L=300 对角线为 8 英寸的光束可以承受 300 磅的最大载荷。
物体坠落的距离与其坠落时间的平方成正比。 一个球在 3 秒钟内落下 144 英尺。
- 写出将距离与时间相关的方程式。
- 物体在 4 秒钟内会掉落多远?
- 回答
-
- \(d=16t^2\)
- 256 英尺
圆的面积随着半径的平方而直接变化。 半径为 6 英寸的圆形披萨的面积为 113.04 平方英寸。
- 写出将面积与半径相关的方程。
- 半径为 9 英寸的披萨的面积是多少?
- 回答
-
- \(A=3.14r^2\)
- 254.34 平方英寸
解决逆变问题
许多应用程序涉及两个反向变化的变量。 随着一个变量的增加,另一个变量的减少。 将它们关联的方程式是\(y=\frac{k}{x}\)。
对于任意两个变量 x 和 y,y 与 x 成反比变化
y=\(\frac{k}{x}\),哪里\(k \ne 0\)
逆变中的 “逆变” 一词是指乘法逆变。 x 的乘法逆为\(\frac{1}{x}\)。
我们解决逆变异问题的方式与解决直接变异问题的方法相同。 只有方程的一般形式发生了变化。 我们将在这里复制程序框,然后将 “直接” 更改为 “反向”。
- 写下逆变异的公式。
- 用给定值代替变量。
- 求解变异常数。
- 写出与 x 和 y 相关的方程。
如果 y 与 x 成反比变化,当 x=8 x 和 y 时 y=20。
- 回答
-
写下逆变异的公式。 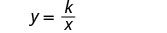
用给定值代替变量。 
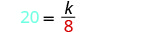
求解变异常数。 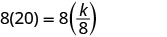

写出与 x 和 y 相关的方程。 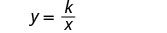
用变异常数代替。 
如果 p 与 q 成反比变化,当 q=12 时 p=30,请找到与 p 和 q 相关的方程。
- 回答
-
\(p=\frac{360}{q}\)
如果 y 与 x 成反比变化,当 x=2 时 y=8,则找出与 x 和 y 相关的方程。
- 回答
-
\(y=\frac{16}{x}\)
汽车的油耗(mpg)与其重量成反比。 一辆重 3100 磅的汽车在高速公路上行驶 26 英里/小时。
- 写下变异方程。
- 一辆重4030磅的汽车的油耗是多少?
- 回答
-
1。
油耗与重量成反比。 首先,我们将命名变量。 让 f = 油耗。
w= 重量。写下逆变异的公式。 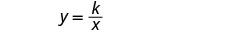
我们将使用 f 代替 y,用 w 代替 x。 
用给定值代替变量。 
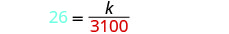
求解变异常数。 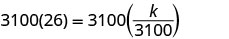

写出与 f 和 w 相关的方程。 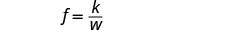
用变异常数代替。 
2。
在 w=4030 时找到 f。 写出与 f 和 w 相关的方程。 
用给定值代替 w。 \(f=\frac{80,600}{4030}\) 简化。 f=20 一辆重 4030 磅的汽车的油耗为 20 英里/小时。
汽车的价值与车龄成反比。 艾琳娜花了2万美元买了一辆已有两年历史的汽车。
- 写下变异方程。
- 当Elena的汽车使用5岁时,它的价值会是多少?
- 回答
-
- \(v=\frac{40,000}{a}\)
- 8,000 美元
清空水池所需的时间与抽水速度成反比。 Lucy 花了 2.5 个小时才使用额定速度为 400 gpm(每分钟加仑)的泵清空游泳池。
- 写下变异方程。
- 她用额定速度为 500 gpm 的泵清空水池需要多长时间?
- 回答
-
- \(t=\frac{1000}{r}\)
- 2 个小时
吉他弦的频率与其长度成反比。 一根 26 英寸长的琴弦振动频率为每秒 440 次。
- 写下变异方程。
- 如果将手指放在琴格上将琴弦的长度缩短到 20 英寸,每秒会有多少振动?
- 回答
-
1。
频率与长度成反比。 为变量命名。 让 f = 频率。
L = 长度。写下逆变异的公式。 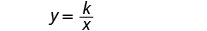
我们将使用 f 代替 y,用 L 代替 x 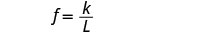
用给定值代替变量。 

求解变异常数。 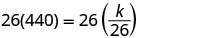

写出与 f 和 L 相关的方程 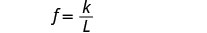
用变异常数代替。 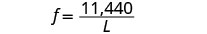
2。
当 L=20 时找到 f。 写出与 f 和 L 相关的方程 \(f=\frac{11,440}{L}\) 用给定值代替 L。 \(f=\frac{11,440}{20}\) 简化。 f=572 一根 20 英寸的吉他弦每秒振动 572 次。
冰融化所需的小时数与空气温度成反比。 假设温度为 65 度时,一块冰在 2 小时内融化。
- 写下变异方程。
- 如果温度为78度,同一块冰需要多少小时才能融化?
- 回答
-
- \(h=\frac{130}{t}\)
- \(1\frac{2}{3}\)小时
打破一块木板所需的力随其长度成反比。 理查德用 24 磅的压力打破了一块 2 英尺长的木板。
- 写下变异方程。
- 打破一块 5 英尺长的木板需要多少磅的压力?
- 回答
-
- \(F=\frac{48}{L}\)
- 9.6 磅


