8.8：解决均匀运动和工作应用

Last updated
Save as PDF

Page ID: 204780

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

解决均匀运动应用程序
解决工作申请

在@@ 开始之前，请参加这个准备测验。

如果您遗漏了问题，请返回列出的部分并查看材料。

特快列车和当地巴士离开芝加哥前往香槟。特快巴士可以在2小时内出行，而当地巴士需要5个小时才能到达。特快巴士的速度比当地公交车的速度快42英里/小时。查找当地公交车的速度。
如果你错过了这个问题，请查看 [链接]。
解决$\frac{1}{3}x+\frac{1}{4}x=\frac{5}{6}$。
如果你错过了这个问题，请查看 [链接]。
解决：$18t^2−30=−33t$。
如果你错过了这个问题，请查看 [链接]。

解决均匀运动应用程序

在前面的章节中，我们已经使用公式 d=rt 解决了均匀运动问题。我们使用了如下所示的表格来整理信息并引导我们得出方程式。

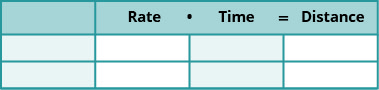
$上图是一个包含 4 列和 3 行的表。第一行是标题行。标题行中的第二列有 “rate” 一词。第三列有 “时间” 一词。第四列显示 “距离”。其余空格为空。$

公式 d=rt 假设我们知道 r 和 t 并用它们来找出 D。如果我们知道 D 和 r 并且需要找到 t，我们将求解 t 的方程并得到公式$t=\frac{D}{r}$

我们还解释了在潮流下飞行或逆流飞行如何影响飞行器的速度。我们将在下一个示例中重新审视这个想法。

示例$\PageIndex{1}$

一架飞机可以在 30 英里/小时的逆风中飞行 200 英里，其时间与在 30 英里/小时的顺风下飞行 300 英里所需的时间相同。飞机的速度是多少？

解决方案

这是一种统一的运动情况。图表将帮助我们直观地了解情况。

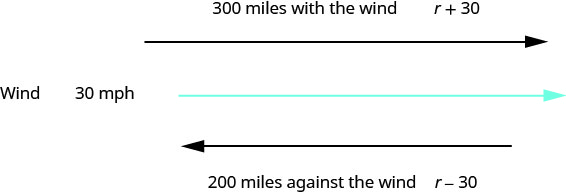
$上图有两个平行箭头。第一支箭头的尖端指向右箭头上方，“300 英里，风 r 加 30”。下面是一条波浪线。在波浪线的左边，上面写着 “风速每小时 30 英里”。下方是一个箭头，其尖端指向左边。下面是 “逆风 200 英里 r 减去 30” 字样。$

我们填写图表来整理信息。

我们正在寻找飞机的速度。	让 r = 飞机的速度。
当飞机随风飞行时，风速会增加，速率为 r+30。
当飞机逆风飞行时，风速会降低，速率为 r−30。
写下费率。在远处写字。由于 d=r∙t，我们求解 t 并得到$\frac{D}{r}$。我们将距离除以每行的速率，然后将表达式放在时间列中。	$。$
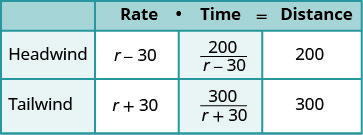我们知道时间是相等的，所以我们写出方程式。	$\frac{200}{r−30}=\frac{300}{r+30}$
我们将两边乘以液晶屏。 200 (r+30) =300 (r−30)
简化。	(r+30) (200) = (r−30) (300)
	200r+6000=300r−9000
解决。	15000=100r 150=r
查看。
对于飞机来说，150 英里/小时是合理的速度吗？是的。如果飞机以 150 英里/小时的速度行驶，风速为 30 英里/小时：
顺风 150+30=180 英里/$\frac{300}{180}=\frac{5}{3}$ 小时小时
逆风 150−30=120 英里/$\frac{200}{120}=\frac{5}{3}$ 小时
时间是相等的，所以它会检查。	飞机以每小时 150 英里的速度行驶。

试试看$\PageIndex{2}$

Link 可以在 3 英里/小时的逆风中骑自行车 20 英里，这与他以 3 英里/小时的顺风行驶 30 英里的时间相同。 Link 的骑行速度是多少？

回答: 15 英里每小时

试试看$\PageIndex{3}$

Judy 可以在 7 英里/小时的逆风中航行 5 英里，这与她在 7 英里/小时的顺风下航行 12 英里的时间相同。没有风的 Judy 的船速度是多少？

回答: 17 英里每小时

在下一个示例中，我们将知道以不同速度行驶不同距离所产生的总时间。

示例$\PageIndex{4}$

周六，贾兹敏训练了 3 个小时。她跑了 8 英里然后骑了 24 英里。她的骑行速度比跑步速度快 4 英里/小时。她的跑步速度是多少？

解决方案

这是一种统一的运动情况。图表将帮助我们直观地了解情况。

$上图是一条直线，两个箭头指向右边。在最左边，在这条线的上方，它写着 “跑”，再往下，稍微超过第一个箭头，上面写着 “自行车”。在这条线稍下方，在最左边，在第一个箭头之前，它写着 “8 英里”；在最右边，第一个箭头之后写着 “12 英里”。对从箭头最左边到最右边的区域进行分组，表示该线的整个长度为 3 小时。$

我们填写图表来整理信息。

我们正在寻找 Jazmine 的跑步速度。	让 r= Jazmine 在跑步 sp
她的骑行速度比跑步速度快 4 英里。	r+4= 她的骑行速度
给出了距离，将其输入到图表中。
由于 d=r∙t，我们求解 t 并得到$t=\frac{D}{r}$ We 将距离除以每行中的速率，然后将表达式放在时间列中。	$。$
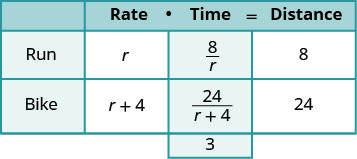写一个单词句子。	她的时间加上骑自行车的时间
翻译句子得出方程式。	$\frac{8}{r}+\frac{24}{r+4}=3$
解决。	$r(r+4)(\frac{8}{r}+\frac{24}{r+4})=3r(r+4)$ $8(r+4)+24r=3r^2+12r$ $8r+32+24r=3r^2+12r$ $32+32r=3r^2+12r$ $0=3r^2−20r−32$ $0=(3r+4)(r−8)$
	(3r+4) =0，(r−8) =0
	$r=−\frac{4}{3}$，r=8
查看。r=8
在这个问题中，负速度是没有意义的，所以 r=8 是解决方案。
8 英里/小时是合理的跑步速度吗？是的。
跑 8 英里每小时，$\frac{8 miles}{8 mph}=1 hour$ 自行车 12 英里每小时，$\frac{24 miles}{12 mph}=2 hours$ 总计 3 个小时。 Jazmine 的跑步速度为 8 英里/小时。

试试看$\PageIndex{5}$

周六，丹尼斯进行了6个小时的越野滑雪。他在上坡滑了20英里，然后向下滑了20英里，回到了起点。他的上坡速度比下坡速度慢 5 英里/小时。丹尼斯的上坡速度和下坡的速度是多少？

回答: 10 英里每小时

试试看$\PageIndex{6}$

托尼开车4个小时回家，在州际公路上行驶208英里，在乡间小路上行驶40英里。如果他在州际公路上的行驶速度比在乡间道路上快15英里/小时，那么他在乡间小路上的速度是多少？

回答: 50 英里每小时

再一次，我们将使用为变量 t 求解的均匀运动公式。

示例$\PageIndex{7}$

汉密尔顿骑着自行车沿着从家到大海的河道上下坡12英里，然后骑上坡回家。他的上坡速度比下坡速度慢8英里/小时。他回家的时间比他去海里花的时间长了两个小时。找出汉密尔顿的下坡速度。

解决方案

这是一种统一的运动情况。图表将帮助我们直观地了解情况。

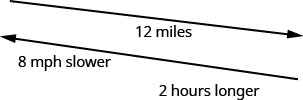
$上图显示了 2 条对角线，平行线指向相反方向。顶线指向右和向下，下方写着 “12 英里”。底线指向左和向上，下方写着 “每小时慢8英里，长2个小时”。$

我们填写图表来整理信息。

我们正在寻找汉密尔顿的下坡速度。	让 r= 汉密尔顿的下坡速度。
他的上坡速度慢了每小时 8 英里。在图表中输入汇率。	h−8= 汉密尔顿的上坡速度
两个方向的距离相同，12 英里。由于 d=r∙t，我们求解 t 并得到$t=\frac{D}{r}$ We 将距离除以每行中的速率，然后将表达式放在时间列中。	$。$
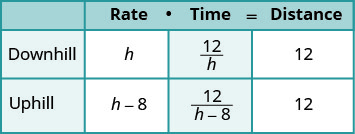写一句关于时间的单词句子。	他上坡的时间比下坡时间长 2 个小时。上坡时间比下坡时间长 2。
翻译句子得出方程式。解决。	$\frac{12}{h−8}=\frac{12}{h}+2$ $h(h−8)(\frac{12}{h−8})=h(h−8)(\frac{12}{h}+2)$ 12h=12 (h−8) +2h (h−8) $12h=12h−96+2h^2−16h$ $0=2h^2−16h−96$ $0=2(h^2−8h−48)$ 0=2 (h−12) (h+4) h−12=0，h+4=0 h=12，h=−4
查看。 12 英里/小时是骑行下坡的合理速度吗？是的。
下坡 12 英里每小时， $\frac{12 miles}{12 mph}=1 hour$
上坡 12−8=4 英里/小时 $\frac{12 miles}{4 mph}=3 hours$
	上坡时间比下坡时间长 2 小时。汉密尔顿的下坡速度为 12 英里/小时。

试试看$\PageIndex{8}$

一个周末，凯拉在离大学75英里的地方骑着自行车回家，然后乘公共汽车回大学。她坐公交车回大学的时间比骑自行车回家花的时间少了两个小时，而且公交车的平均时速比凯拉的骑行速度快了10英里/小时。查找 Kayla 的骑行速度。

回答: 15 英里每小时

试试看$\PageIndex{9}$

维多利亚沿着一条平坦的小径慢跑12英里到公园，然后在18英里的丘陵小径上慢跑返回。她在丘陵小径上慢跑每小时比在平坦的小径上慢一英里，而且她的回程花了两个小时。在平坦的小径上找到她的慢跑速度。

回答: 6 英里每小时

解决工作申请

假设 Pete 可以在 10 个小时内粉刷一个房间。如果他以稳定的速度工作，他将在1小时内画出房间$\frac{1}{10}$的画面。如果艾丽西亚要花 8 个小时来粉刷同一个房间，那么 1 小时后她就会画$\frac{1}{8}$出这个房间。如果 Pete 和 Alicia 一起工作（并且不干扰彼此的进步），他们要花多长时间才能粉刷房间？

这是一个典型的 “工作” 应用程序。这里涉及三个数量——两个人各自独自完成工作所花费的时间，以及他们共同完成工作所花费的时间。

我们回去找皮特和艾丽西娅粉刷房间吧 我们将假设他们一起粉刷房间所花费的小时数。 因此，在一起工作1小时后，他们就完成$\frac{1}{t}$了工作。

一小时后 Pete 就完成$\frac{1}{10}$了这份工作。艾丽西亚做$\frac{1}{8}$了这份工作。他们一起完成$\frac{1}{t}$了这项工作。

我们可以用 “方程” 一词对其进行建模，然后将其转换为有理方程。为了找出他们合作所花费的时间，我们求解了 t。

	$。$
	$。$
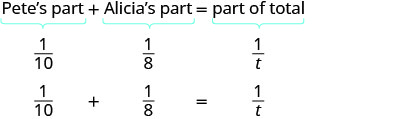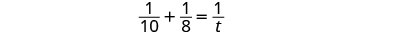乘以液晶屏，40t	$。$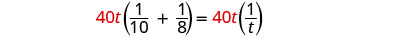
分发。	$。$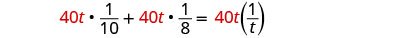
简化并解决。	$。$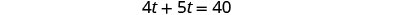
	$。$
	$。$
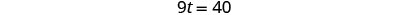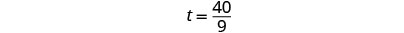我们将写成混合数字，这样我们就可以将其转换为小时和分钟。	$。$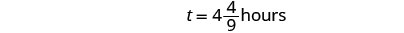
请记住，1 小时 = 60 分钟。	$。$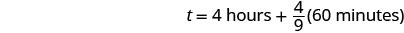
乘以，然后四舍五入到最接近的分钟。	$。$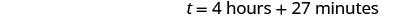
	Pete 和 Alica 要花大约 4 小时 27 分钟才能粉刷房间。

请记住，两个人一起完成一份工作所花费的时间应该少于任何一个人单独完成工作所花费的时间。

示例$\PageIndex{10}$

每周八卦杂志有一篇关于公主宝贝的重大报道，编辑希望该杂志尽快出版。她要求打印机额外运行一台印刷机以更快地完成打印。按 #1 需要 6 个小时才能完成工作，按 #2 需要 12 个小时才能完成工作。在两台印刷机一起运行的情况下，打印机需要多长时间才能打印杂志？

解决方案

这是一个工作问题。图表将帮助我们整理信息。

假设 t= 一起完成任务所需的小时数。
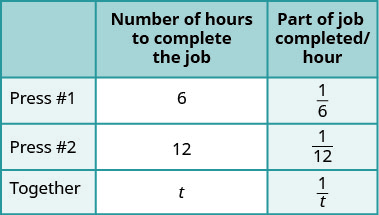输入每项作业的工时，按 #1、按 #2 以及它们何时协同工作。如果 Press #1 上的作业需要 6 个小时，则该作业将在 1 小时$\frac{1}{6}$内完成。同样，可以找到 Press #2 工作已完成的部分/小时以及它们何时协同工作。	$。$
写一个单词句子。
由 Press #1 完成的部分加上 Press #2 完成的部分等于总完成的数量。
转换为方程。	$。$
解决。	$。$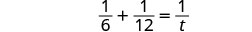
乘以液晶屏，12t。	$。$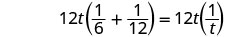
简化。	$。$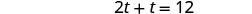
	$。$
	$。$
	当两台印刷机都在运行时，需要4个小时才能完成这项工作。

试试看$\PageIndex{11}$

一个园丁可以在 4 小时内修剪一个高尔夫球场，而另一个园丁可以在 6 小时内修剪同一个高尔夫球场。如果两个园丁一起修剪高尔夫球场需要多长时间？

回答: 2 小时 24 分钟

试试看$\PageIndex{12}$

Carrie 可以在 7 个小时内在花园里除草，而她妈妈可以在 3 个小时内除草。他们两个一起工作要花多长时间？

回答: 2 小时 6 分钟

示例$\PageIndex{13}$

Corey 可以在 4 小时内铲掉人行道和车道上的所有积雪。如果他和他的双胞胎凯西一起工作，他们可以在两个小时内完成铲雪。 Casey 要花多少小时才能独自完成这项工作？

解决方案

这是一个工作应用程序。图表将帮助我们整理信息。
我们正在寻找 Casey 要花多少小时才能独自完成这项工作。
假设 t= Casey 完成所需的小时数。
输入 Corey、Casey 每份工作的工时以及他们在一起工作的时间。如果 Corey 需要 4 个小时，则在 1 小时内$\frac{1}{4}$完成作业。同样，可以发现 Casey 的工作已完成/工作时间，以及他们何时一起工作。	$。$
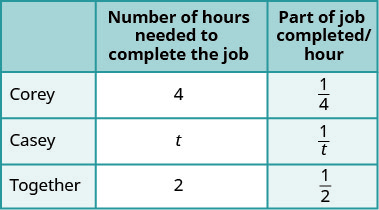写一个单词句子。
由 Corey 完成的部分加上 Casey 完成的部分等于总完成的数量。
转换为方程式：	$。$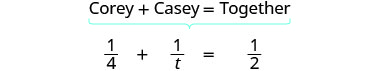
解决。	$。$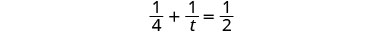
乘以液晶屏，4t。	$。$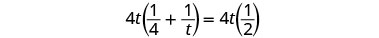
简化。	$。$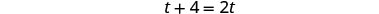
	$。$
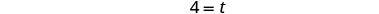	要让 Casey 独自完成这项工作需要 4 个小时。

试试看$\PageIndex{14}$

两根软管可以在 10 小时内填满游泳池。一根软管自己填满水池需要 26 个小时。另一根单独工作的软管需要多长时间才能填满水池？

回答: 16.25 小时

试试看$\PageIndex{15}$

Cara 和 Cindy 一起工作可以在 4 个小时内完成院子里的耙子。辛迪独自工作，需要6个小时才能把院子里耙出来。 Cara 独自挖院子要花多长时间？

回答: 12 个小时

练习成就完美

求解均匀运动应用程序

在以下练习中，求解均匀运动应用程序

试试看$\PageIndex{16}$

玛丽乘坐直升机进行观光旅游，该直升机可以在逆风 35 英里/小时的逆风下飞行 450 英里，与在 35 英里/小时的顺风下行驶 702 英里的时间相同。找出直升机的速度。

解决方案

160 mph

练习$\PageIndex{17}$

私人飞机可以在 25 英里/小时的逆风下飞行 1210 英里，其顺风速度为 25 英里/小时可以飞行 1694 英里的时间相同。找到喷气式飞机的速度。

试试看$\PageIndex{18}$

一艘船在下游行驶 140 英里，同时向上游行驶 92 英里。当前的速度为 6 英里/小时。船的速度是多少？

回答: 29 英里/小时

练习$\PageIndex{19}$

达林可以在 4 英里/小时的风速下滑板 2 英里，时间与他在 4 英里/小时的风速下滑板 6 英里的时间相同。找出没有风的 Darrin 滑板的速度。

试试看$\PageIndex{20}$

Jane 花了 2 个小时骑着越野车探索一座山。当她上坡 40 英里时，她的行驶速度比到达山顶时慢 5 英里/小时，沿着山顶骑行 12 英里。她在峰会上的评分是多少？

回答: 30 英里每小时

练习$\PageIndex{21}$

吉尔想减肥，所以她计划锻炼一天。她总共花了2个小时骑自行车和慢跑。她骑了12英里然后慢跑了6英里。她的慢跑速度比骑行速度低 10 英里/小时。她慢跑时的分数是多少？

试试看$\PageIndex{22}$

比尔想尝试不同的水上飞船。他乘坐摩托艇向下游行驶了62英里，乘坐摩托艇向下游行了27英里。他在摩托艇上的速度比摩托艇快10英里/小时。比尔在水上总共花了4个小时。他在摩托艇上的速度是多少？

回答: 20 英里每小时

练习$\PageIndex{23}$

南希开了 3 个小时的车程。在被暴风雨困住之前，她跑了 50 英里。然后，她以每小时 9 英里/小时的速度行驶 68 英里，比天气晴朗时开了 68 英里。暴风雨中她的速度是多少？

试试看$\PageIndex{24}$

切斯特骑着自行车上坡 24 英里，然后以比上坡快 2 英里/小时的速度下坡。如果他上坡的时间比下坡的时间长 2 个小时，我，他的上坡速度是多少？

回答: 4 英里每小时

练习$\PageIndex{25}$

马修慢跑到 12 英里外的朋友家，然后搭车回家。他在那里慢跑的时间比骑回去的时间长了两个小时。他的慢跑速度比骑行时的速度慢25英里/小时。他的慢跑率是多少？

试试看$\PageIndex{26}$

哈德森乘坐喷气式飞机行驶 1080 英里，然后开车 240 英里去参加商务会议。喷气式飞机的行驶速度比汽车的速度快 300 英里/小时，汽车的行驶时间比喷气式飞机长 1 个小时。汽车的速度是多少？

回答: 60 英里每小时

练习$\PageIndex{27}$

内森在沥青路上行走了 12 英里。他在穿过森林的碎石路上走了12英里回到自己的车里。在沥青上，他每小时的行走速度比在碎石上行走快2英里。在砾石上行走的时间比在沥青上行走的时间长了一个小时。他在碎石上行走的速度有多快？

试试看$\PageIndex{28}$

约翰可以以 50 英里/小时的风速驾驶飞机 2800 英里，同时他可以逆风行驶 2400 英里。如果风速为 50 英里/小时，请找出他的飞机的速度。

回答: 650 mph

练习$\PageIndex{29}$

吉姆的快艇可以在3英里/小时的电流下向上行驶20英里，其下游行驶时间与以3英里/小时的当前速度向下游行驶22英里的时间相同。找出吉姆船的速度。

试试看$\PageIndex{30}$

Hazel 需要乘飞机和租车去孙女家。她乘飞机旅行 900 英里，开车旅行 250 英里。飞机的行驶速度比汽车快 250 英里/小时。如果她驾驶租车的时间比乘坐飞机多 2 个小时，请找出汽车的速度。

回答: 50 英里每小时

练习$\PageIndex{31}$

Stu 昨天训练了 3 个小时。他跑了 14 英里然后骑了 40 英里。他的骑行速度比跑步速度快 6 英里/小时。他的跑步速度是多少？

试试看$\PageIndex{32}$

在开车9小时回家时，沙龙在州际公路上行驶了390英里，在乡间小路上行驶了150英里。她在州际公路上的速度比在乡间小路上的速度高15分。她在乡间小路上的速度是多少？

回答: 50 英里每小时

练习$\PageIndex{33}$

两个姐妹喜欢骑自行车。塔玛拉的速度可以比她的妹妹萨曼莎快 4 英里/小时。如果萨曼莎比塔玛拉长 1 个小时才能行驶 80 英里，那么萨曼莎骑自行车的速度有多快？

解决工作申请

在以下练习中，求解工作申请。

试试看$\PageIndex{34}$

迈克是一位经验丰富的瓦工，可以在3个小时内修建一堵墙，而他的儿子正在学习，可以在6个小时内完成这项工作。他们一起筑墙需要多长时间？

回答: 2 个小时

练习$\PageIndex{35}$

Sam 需要 4 个小时才能在前面的草坪上耙，而他的兄弟 Dave 可以在 2 小时内耙草坪。他们一起挖草坪要花多长时间？

试试看$\PageIndex{36}$

玛丽可以在6小时内打扫她的公寓，而她的室友可以在5个小时内打扫公寓。如果他们一起工作，他们需要多长时间才能打扫公寓？

回答: 2 小时 44 分钟

练习$\PageIndex{37}$

布莱恩可以在 6 小时内铺设一块混凝土板，而 Greg 可以在 4 小时内完成。如果布莱恩和格雷格一起工作，需要多长时间？

试试看$\PageIndex{38}$

Leeson 可以在 4 小时内校对一份报纸副本。如果瑞安帮忙，他们可以在3小时内完成这项工作。 Ryan 独自完成工作需要多长时间？

回答: 12 个小时

练习$\PageIndex{39}$

Paul 可以在 3 小时内清理教室的地板。当他的助手帮助他时，这项工作需要2个小时。助手一个人做要花多长时间？

试试看$\PageIndex{40}$

Josephine 可以在 5 个小时内更正学生的试卷，但如果老师的助手帮忙，他们将需要 3 个小时。助手一个人做要花多长时间？

回答: 7 小时 30 分钟

练习$\PageIndex{41}$

八岁的李维独自洗车需要2.5个小时。如果他爸爸帮助他，那就需要一个小时。李维斯的爸爸自己洗车要花多长时间？

试试看$\PageIndex{42}$

杰克逊可以在7小时内从房屋中取出带状疱疹，而马丁可以在5小时内清除带状疱疹。如果他们一起工作，他们需要多长时间才能取出带状疱疹？

回答: 2 小时 55 分钟

练习$\PageIndex{43}$

归根结底，多迪可以在15分钟内打扫她的美发沙龙。和她一起工作的安可以在30分钟内打扫沙龙。如果他们一起工作，他们要花多长时间才能打扫商店？

试试看$\PageIndex{44}$

罗纳德可以在 4 小时内铲掉车道，但如果他的兄弟唐纳德帮忙，那将需要 2 个小时。唐纳德独自铲车道要花多长时间？

回答: 4 个小时

练习$\PageIndex{45}$

Tina 花了 3 个小时才能冻结她的节日饼干，但如果 Candy 帮助她则需要 2 个小时。 Candy 自己给节日饼干加霜需要多长时间？

日常数学

试试看$\PageIndex{46}$

达娜喜欢带她的狗去散步，但有时候她的狗会逃脱，她必须追着他。 Dana walking 了她的狗 7 英里，但随后不得不跑了 1 英里，总共花了 2.5 个小时陪伴她的狗。她的跑步速度比步行速度快 3 英里/小时。找出她的行走速度

回答: 3 英里每小时

练习$\PageIndex{47}$

Ken 和 Joe 离开公寓去参加 45 英里外的足球比赛。肯开车速度快 30 英里/小时 Joe 可以骑自行车。如果 Joe 玩游戏的时间比 Ken 长 2 个小时，那么 Joe 的速度是多少？

写作练习

练习$\PageIndex{48}$

在示例中，解 h=−4 被划掉。解释原因。

练习$\PageIndex{49}$

宝拉和尤基是室友。 Paula 花了 3 个小时来打扫他们的公寓。 Yuki 打扫公寓需要 4 个小时。这个方程$\frac{1}{3}+\frac{1}{4}=\frac{1}{t}$可以用来求出 t，即他们俩共同努力打扫公寓所花费的小时数。解释这个方程是如何模拟情况的。

自检

ⓐ 完成练习后，使用这份清单来评估你对本节目标的掌握程度。

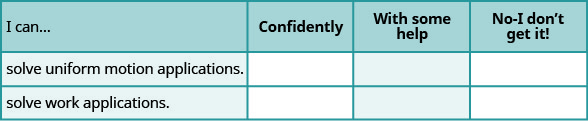
$此表有三行四列。第一行是标题行，它标记了每列。第一列标有 “我能...”，第二列标记为 “自信地”，第三列标记为 “有帮助”，最后一列标记为 “不，我不明白”。在 “我能...” 列中，下一行是 “解决均匀运动应用程序”。下一行是 “解决工作申请”。其余列为空白。$

ⓑ 在 1-10 的等级中，根据你在清单上的回复，你会如何评价你对本节的掌握程度？你怎么能改善这个？