7.6E：练习

练习成就完美

使用 “零积分” 属性

在以下练习中，求解。

练习 1

$(x−3)(x+7)=0$

回答

$x=3$，$x=−7$所以解决方案集是：$\{3, -7\}$

练习 2

$(y−11)(y+1)=0$

练习 3

$(3a−10)(2a−7)=0$

回答

$a=\frac{10}{3}$，$a=\frac{7}{2}$所以解决方案集是：$\Big\{\tfrac{10}{3}, \tfrac{7}{2}\Big\}$

练习 4

$(5b+1)(6b+1)=0$

练习 5

$6m(12m−5)=0$

回答

$m=0$，$m=\frac{5}{12}$所以解决方案集是：$\Big\{0, \tfrac{5}{12}\Big\}$

练习 6

$2x(6x−3)=0$

练习 7

$(y−3)^2=0$

回答

$y=3$所以解决方案集是：$\{3\}$

练习 8

$(b+10)^2=0$

练习 9

$(2x−1)^2=0$

回答

$x=\frac{1}{2}$所以解决方案集是：$\Big\{\tfrac{1}{2}\Big\}$

练习 10

$(3y+5)^2=0$

通过分解求解二次方程

在以下练习中，求解。

练习 11

$x^2+7x+12=0$

回答

$x=−3$，$x=−4$所以解决方案集是：$\{-3, -4\}$

练习 12

$y^2−8y+15=0$

练习 13

$5a^2−26a=24$

回答

$a=−\tfrac{4}{5}$，$a=6$所以解决方案集是：$\Big\{−\tfrac{4}{5}, 6\Big\}$

练习 14

$4b^2+7b=−3$

练习 15

$4m^2=17m−15$

回答

$m=\frac{5}{4}$，$m=3$所以解决方案集是：$\Big\{\tfrac{5}{4}, 3\Big\}$

练习 16

$n^2=5−6n$

练习 17

$7a^2+14a=7a$

回答

$a=−1$，$a=0$所以解决方案集是：$\{-1, 0\}$

练习 18

$12b^2−15b=−9b$

练习 19

$49m^2=144$

回答

$m=\frac{12}{7}$，$m=−\frac{12}{7}$所以解决方案集是：$\Big\{−\tfrac{12}{7}, \tfrac{12}{7}\Big\}$

练习 20

$625=x^2$

练习 21

$(y−3)(y+2)=4y$

回答

$y=−1$，$y=6$所以解决方案集是：$\{-1, 6\}$

练习 22

$(p−5)(p+3)=−7$

练习 23

$(2x+1)(x−3)=−4x$

回答

$x=\frac{3}{2}$，$x=−1$所以解决方案集是：$\Big\{-1,\tfrac{3}{2}\Big\}$

练习 24

$(x+6)(x−3)=−8$

练习 25

$16p^3=24p^2−9p$

回答

$p=0$，$p=\frac{3}{4}$所以解决方案集是：$\Big\{0,\tfrac{3}{4}\Big\}$

练习 26

$m^3−2m^2=−m$

练习 27

$20x^2−60x=−45$

回答

$x=\frac{3}{2}$所以解决方案集是：$\Big\{\tfrac{3}{2}\Big\}$

练习 28

$3y^2−18y=−27$

求解由二次方程建模的应用程序

在以下练习中，求解。

练习 29

两个连续整数的乘积为 56。 找出整数。

回答

7 和 8；−8 和 −7

练习 30

两个连续整数的乘积为 42。 找出整数。

练习 31

矩形地毯的面积为 28 平方英尺。 长度比宽度多三英尺。 找出地毯的长度和宽度。

回答

4 英尺和 7 英尺

练习 32

矩形挡土墙的面积为 15 平方英尺。 墙的高度比其长度小两英尺。 找出墙的高度和长度。

练习 33

三角旗的形状像直角三角形，斜边 10 英尺。 三角旗一侧的长度比另一侧的长度长两英尺。 找出三角旗两边的长度。

回答

6 英尺和 8 英尺

练习 34

反射池的形状像直角三角形，一条腿沿着建筑物的墙壁。 斜边比建筑物沿线的一侧长 9 英尺。 第三面比建筑物沿线的一侧长 7 英尺。 找出反射池所有三边的长度。

混合练习

在以下练习中，求解。

练习 35

(x+8) (x−3) =0

回答

$x=−8, \; x=3$所以解决方案集是：$\{-8, 3\}$

练习 36

(3y−5) (y+7) =0

练习 37

$p^2+12p+11=0$

回答

$p=−1, \;p=−11$所以解决方案集是：$\{-11, -1\}$

练习 38

$q^2−12q−13=0$

练习 39

$m^2=6m+16$

回答

$m=−2, \; m=8$所以解决方案集是：$\{-2, 8\}$

练习 40

$4n^2+19n=5$

练习 41

$a^3−a^2−42a=0$

回答

$a=0, \;a=−6, \;a=7$所以解决方案集是：$\{-6, 0, 7\}$

练习 42

$4b^2−60b+224=0$

练习 43

两个连续整数的乘积为 110。 找出整数。

回答

10 和 11；−11 和 −10

练习 44

直角三角形的一条腿的长度比另一条腿的长度多三条。 如果斜边为 15，则求出两条腿的长度。

日常数学

练习 45

露台面积如果方形露台的两侧增加 4 英尺，则露台的面积将为 196 平方英尺。 求解方程 (s+4) 2=196 (s+4) 2=196 让 s 得出露台一侧的长度。

回答

10 英尺

练习 46

Watermelon drop 西瓜从建筑物的第十层掉落。 求解 tt 的方程 −16t2+144=0−16t2+144=0，得出西瓜到达地面所需的秒数。

写作练习

练习 47

解释如何求解二次方程。 你预计二次方程会得到多少答案？

回答

答案可能因解释而异。 二次方程的解应该不超过 2 个。 它通常有两个解决方案，但有时，它可能有一个重复的解决方案，甚至没有解决方案。

练习 48

举一个二次方程的示例，该方程具有 GCF，且该方程的解都不为零。

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

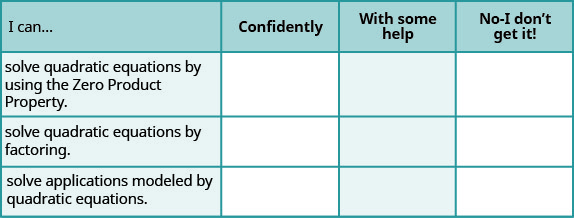
b. 总的来说，看完清单后，你认为你为下一节做好了充分的准备吗？ 为什么或者为什么不呢？