7.6: 二次方程
- Page ID
- 204541
在本节结束时,您将能够:
- 使用零积属性求解二次方程
- 求解二次方程分解
- 求解由二次方程建模的应用程序
我们已经求解了线性方程,即形式的方程式\(a x+b y=c\)。 在线性方程中,变量没有指数。 二次方程是将变量求平方的方程。 下面列出了一些二次方程的示例:
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
最后一个方程似乎没有将变量求平方,但是当我们简化左边的表达式时,就会得到\(n^{2}+n\)。
二次方程的一般形式为\(a x^{2}+b x+c=0\),with\(a \neq 0\)。
这种形式的方程\(a x^{2}+b x+c=0\)称为二次方程。
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
为了求解二次方程,我们需要的方法不同于我们在求解线性方程时使用的方法。 我们将在此处介绍一种方法,然后在后面的章节中介绍其他几种方法。
使用零积属性求解二次方程
我们将首先使用零积属性求解一些二次方程。 零产品属性表示,如果两个数量的乘积为零,则必须至少有一个数量为零。 获得等于零的乘积的唯一方法是乘以零本身。
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
解决:\((x+1)(x-4)=0\)
- 回答
-



解决:\((x-3)(x+5)=0\)
- 回答
-
\(x=3, x=-5\)
解决:\((y-6)(y+9)=0\)
- 回答
-
\(y=6, y=-9\)
在求解使用零积属性产生的线性方程时,我们通常会比上一个示例多做一点工作。
解决:\((5 n-2)(6 n-1)=0\)
- 回答
-
\((5 n-2)(6 n-1)=0\) 使用零积属性将
每个因子设置为 0。\(5 n-2=0 \)
\(6 n-1=0\) 求解方程式。 \(n=\frac{2}{5}\) \(n = \frac{1}{6}\) 检查你的答案。 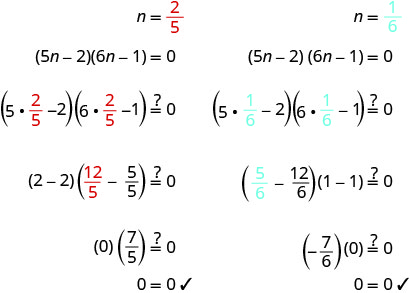
解决:\((3 m-2)(2 m+1)=0\)
- 回答
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
解决:\((4 p+3)(4 p-3)=0\)
- 回答
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
请注意,当我们检查解时,每个解只有一个因子等于零。 但是两种解决方案的产品均为零。
解决:\(3 p(10 p+7)=0\)
- 回答
-
\(3p(10p+7)=0\) 使用零积属性将
每个因子设置为 0。3p=0 10p+7=0 求解方程式。 p=0 10p=−7 \(p=-\frac{7}{10}\) 检查你的答案。 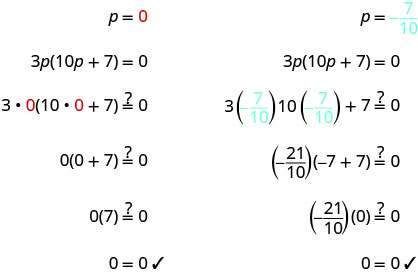
解决:\(2 u(5 u-1)=0\)
- 回答
-
\(u=0, u=\frac{1}{5}\)
解决:\(w(2 w+3)=0\)
- 回答
-
\(w=0, w=-\frac{3}{2}\)
在下一个示例中,似乎只有一个因素。 但是请记住,这\((y-8)^{2}\)意味着\((y-8)(y-8)\)。
解决:\((y-8)^{2}=0\)
- 回答
-
\((y−8)^{2}=0\) 将左侧重写为产品。 (y−8) (y−8) =0 使用零乘积属性并将每个因子
设置为 0。y−8=0 y−8=0 求解方程式。 y=8 y=8 当解决方案重复出现时,我们称之
为双根。检查你的答案。 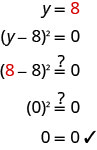
解决:\((x+1)^{2}=0\)
- 回答
-
\(x=1\)
解决:\((v-2)^{2}=0\)
- 回答
-
\(v=2\)
通过分解求解二次方程
到目前为止,我们在本节中求解的每个方程都有一面是因子分解的。 要使用零积属性,必须对二次方程进行分解,一侧为零。 因此,我们一定要从标准形式的二次方程开始\(a x^{2}+b x+c=0\)。 然后我们将左边的表达式分解。
解决:\(x^{2}+2 x-8=0\)
- 回答
-

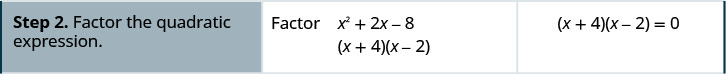



解决:\(x^{2}-x-12=0\)
- 回答
-
\(x=4, x=-3\)
解决:\(b^{2}+9 b+14=0\)
- 回答
-
\(b=-2, b=-7\)
通过@@
- 以标准形式写下二次方程\(a x^{2}+b x+c=0\)。
- 将二次表达式分解为因子。
- 使用 “零积分” 属性。
- 求解线性方程。
- 查看。
在分解之前,我们必须确保二次方程为标准形式。
解决:\(2 y^{2}=13 y+45\)
- 回答
-
\(2 y^{2}=13 y+45\) 用标准形式写下二次方程。 \(2 y^{2}-13 y-45=0\) 将二次表达式分解为因子。 \((2 y+5)(y-9)=0\) 使用零积属性
将每个因子设置为 0。\(2 y+5=0\) \(y-9=0\) 求解每个方程。 \(y=-\frac{5}{2}\) \(y=9\) 检查你的答案。 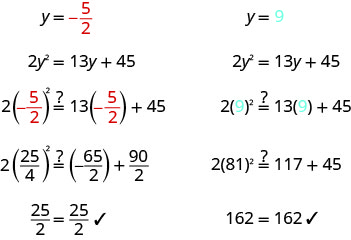
解决:\(3 c^{2}=10 c-8\)
- 回答
-
\(c=0, c=\frac{4}{3}\)
解决:\(2 d^{2}-5 d=3\)
- 回答
-
\(d=3, d=-\frac{1}{2}\)
解决:\(5 x^{2}-13 x=7 x\)
- 回答
-
\(5 x^{2}-13 x=7 x\) 用标准形式写下二次方程。 \(5 x^{2}-20 x=0\) 将方程的左侧考虑在内。 \(5 x(x-4)=0\) 使用零积属性
将每个因子设置为 0。\(5x=0\) \(x−4=0\) 求解每个方程。 \(x=0\) \(x=4\) 检查你的答案。 
解决:\(6 a^{2}+9 a=3 a\)
- 回答
-
\(a=0, a=-1\)
解决:\(45 b^{2}-2 b=-17 b\)
- 回答
-
\(b=0, b=-\frac{1}{3}\)
通过分解求解二次方程将利用你在本章中学到的所有分解技术! 你认出下一个例子中的特殊产品图案吗?
解决:\(144 q^{2}=25\)
- 回答
-
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
解决:\(25 p^{2}=49\)
- 回答
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
解决:\(36 x^{2}=121\)
- 回答
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
下一个示例中的左边是分数的,但右边不为零。 要使用零积属性,方程的一侧必须为零。 我们将乘以因子,然后以标准形式写出方程。
解决:\((3 x-8)(x-1)=3 x\)
- 回答
-
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
解决:\((2 m+1)(m+3)=12 m\)
- 回答
-
\(m=1, m=\frac{3}{2}\)
解决:\((k+1)(k-1)=8\)
- 回答
-
\(k=3, k=-3\)
零积特性也适用于三个或更多因子的乘积。 如果乘积为零,则至少有一个因子必须为零。 我们可以使用零积属性求解一些度数大于二度的方程,就像我们求解二次方程一样。
解决:\(9 m^{3}+100 m=60 m^{2}\)
- 回答
-
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
解决:\(8 x^{3}=24 x^{2}-18 x\)
- 回答
-
\(x=0, x=\frac{3}{2}\)
解决:\(16 y^{2}=32 y^{3}+2 y\)
- 回答
-
\(y=0, y=\frac{1}{4}\)
在下一个示例中,当我们将二次方程分解时,我们将得到三个因子。 但是,第一个因子是一个常数。 我们知道该因子不能等于 0。
解决:\(4 x^{2}=16 x+84\)
- 回答
-
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
解决:\(18 a^{2}-30=-33 a\)
- 回答
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
解决:\(123 b=-6-60 b^{2}\)
- 回答
-
\(b=2, b=\frac{1}{20}\)
求解由二次方程建模的应用程序
我们之前在转换为线性方程的应用程序中使用的问题解决策略对于转换为二次方程的应用程序同样有效。 我们将在这里复制问题解决策略,以便我们可以将其用作参考。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 用一句话用所有重要信息重述问题可能会有所帮助。 然后,将英语句子翻译成代数方程。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
两个连续整数的乘积是 “\(132 .\)查找整数”。
- 回答
-
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
两个连续整数的乘积是 “\(240 .\)查找整数”。
- 回答
-
\(-15,-16\)和\(15,16\)
两个连续整数的乘积是 “\(420 .\)查找整数”。
- 回答
-
\(-21,-20\)和\(20,21\)
你对前面示例的解决方案之一那对负整数感到惊讶吗? 两个正整数的乘积和两个负整数的乘积都得出 132。
在某些应用中,负解将由代数产生,但对于这种情况来说并不现实。
矩形花园的面积为 15 平方英尺。 花园的长度比宽度多两英尺。 找出花园的长度和宽度。
- 回答
-
第 1 步。 阅读问题。 在涉及几何图形的问题中,草图可以帮助你直观地看到情况。 
第 2 步。 确定你在找什么。 我们正在寻找长度和宽度。 第 3 步。 说出你要找的东西。
长度比宽度多两英尺。假设 W = 花园的宽度。
W + 2 = 花园的长度第 4 步。 翻译成方程式。
在句子中重述重要信息。
矩形花园的面积为 15 平方英尺。使用矩形面积的公式。 \(A=L \cdot W\) 在变量中替换。 \(15=(W+2) W\) 第 5 步。 求解方程。 先分发。 \(15=W^{2}+2 W\) 一边为零。 \(0=W^{2}+2 W-15\) 将三项式分解为因子。 \(0=(W+5)(W-3)\) 使用 “零积分” 属性。 \(0=W+5\) \(0=W−3\) 求解每个方程。 \(−5=W\) \(3=W\) 由于 W 是花园的宽度,
因此将其设为
负数是没有意义的。 我们消除 W 的这个值。\(W=−5\) cannot be the width, since it's negative.
\(W=3\)\(3=W\)
宽度为 3 英尺。找出长度的值。 \(\text{length}=W+2\) \(\text{length}=3+2\) \(\text{length}=5\) 长度为 5 英尺。 第 6 步。 检查答案。
答案有意义吗?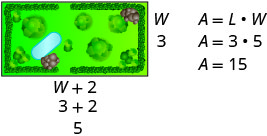
是的,这是有道理的。 第 7 步。 回答问题。 花园的宽度为 3 英尺
,长度为 5 英尺。
矩形标志的面积为 30 平方英尺。 标志的长度比宽度多一英尺。 找出标志的长度和宽度。
- 回答
-
55 英尺和 66 英尺
矩形露台的面积为 180 平方英尺。 露台的宽度比长度小三英尺。 找出露台的长度和宽度。
- 回答
-
12 英尺和 15 英尺
在前面的章节中,我们使用了毕达哥拉斯定理\(\left(a^{2}+b^{2}=c^{2}\right)\)。 它给出了直角三角形的腿部和斜边之间的关系。
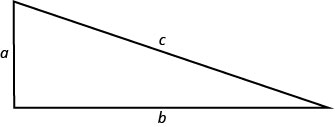
我们将在下一个示例中使用这个公式。
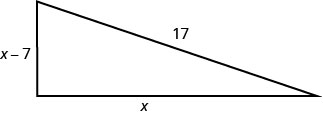
贾斯汀想在她后院的角落放一个直角三角形的甲板,如下所示。 斜边将长达 17 英尺。 一边的长度将比另一边的长度小 7 英尺。 找出甲板两侧的长度。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 我们正在寻找甲板两侧
的长度。第 3 步。 说出你要找的东西。
一侧比另一侧少 7。假设 x = 牌组一侧的长度
x − 7 = 另一边的长度第 4 步。 翻译成方程式。
由于这是一个直角三角形,我们可以使用
毕达哥拉斯定理。\(a^{2}+b^{2}=c^{2}\) 在变量中替换。 \(x^{2}+(x-7)^{2}=17^{2}\) 第 5 步。 求解方程。 \(x^{2}+x^{2}-14 x+49=289\) 简化。 \(2 x^{2}-14 x+49=289\) 它是一个二次方程,所以在一边求零。 \(2 x^{2}-14 x-240=0\) 因子是最大的共同因素。 \(2\left(x^{2}-7 x-120\right)=0\) 将三项式分解为因子。 \(2(x-15)(x+8)=0\) 使用 “零积分” 属性。 \(2\neq 0\) \(x−15=0\) \(x+8=0\) 解决。 \(2\neq 0\) \(x=15\) \(x=-8\) 因为\(x\)是三角形的一边,所以\(x=−8\)没有
意义。\(2\neq 0\) \(x=15\) \(\cancel{x=−8}\) 找出另一边的长度。 如果一边的长度为 \(x=15\) 那么另一边的长度是 \(x-7\) \(15 - 7 = 8\) 8 是另一边的长度。 第 6 步。 检查答案。
这些数字有意义吗?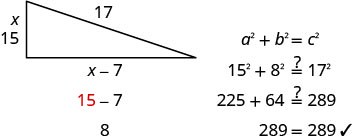
第 7 步。 回答问题。 甲板的两侧分别为 8、15 和 17 英尺。
船帆是一个直角三角形。 帆一侧的长度比另一侧长 7 英尺。 斜边为 13。 找出帆两侧的长度。
- 回答
-
5 英尺和 12 英尺
冥想花园呈直角三角形,一条腿 7 英尺。 斜边的长度比另一条腿的长度多一条。 找出斜边和另一条腿的长度。
- 回答
-
24 英尺和 25 英尺
关键概念
- 零产品属性 If\(a \cdot b=0\),则要么是 a=0 或 b=0,要么两者兼而有之。 参见示例。
- 通过@@ 分解求解二次方程要通过分解求解二次方程:参见示例。
- 以标准形式写下二次方程\(a x^{2}+b x+c=0\)。
- 将二次表达式分解为因子。
- 使用 “零积分” 属性。
- 求解线性方程。
- 查看。
- 使用问题解决策略来解决单词问题参见示例。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 用一句话用所有重要信息重述问题可能会有所帮助。 然后,将英语句子翻译成代数方程。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
词汇表
- 二次方程
- 是将变量求平方的方程。
- 零产品属性
- 零积物属性指出,如果两个数量的乘积为零,则至少有一个数量为零。


