7.5: 分解多项式的通用策略
- Page ID
- 204576
在本节结束时,您将能够:
- 识别并使用适当的方法将多项式完全分解
识别并使用适当的方法完全分解多项式
现在,您已经熟悉了本课程中需要的所有保理方法。 (在你的下一个代数课程中,更多方法将添加到你的曲目中。) 下图总结了我们介绍的所有分解方法。 图中\(\PageIndex{1}\)概述了在分解多项式时应使用的策略。

- 有最大的共同因素吗?
- 把它排除在外。
- 多项式是二项式、三项式还是超过三个项?
- 如果是二项式:
是总和吗?- 正方形? 平方和不分解。
- 多维数据集? 使用立方体总和模式。
- 正方形? 因子是共轭物的乘积。
- 多维数据集? 使用立方体差异图案。
- 如果是三项式:
是这样的\(x^{2}+b x+c ?\)吗? 撤消 FOIL。
是这样的吗\(a x^{2}+b x+c\)?- 如果 aa 和 cc 是正方形,请检查它是否符合三项式方形图案。
- 使用反复试验或 “ac” 方法。
- 如果它有三个以上的术语:
使用分组方法。
- 如果是二项式:
- 查看。
- 完全考虑了吗?
- 这些因子会乘回原来的多项式吗?
请记住,如果除单项式以外,多项式的因子是素数,则该多项式是完全分解的!
完全考虑以下因素:\(4 x^{5}+12 x^{4}\)
- 回答
-
\ (\ begin {array} {ll}\ text {有 GCF 吗? } &\ text {是的,} 4 x^ {4} & 4 x^ {5} +12 x^ {4}\\\ text {除去 GCF。} & &4 x^ {4} (x+3)\\ text {在括号中,是二项式,a} &\\ text {三项式,还是有三个以上的术语? } &\ text {二项式。} &\\\ quad\ text {是总和吗? } &\ text {是的。}\\\ quad\ text {Of squares? 多维数据集? } &\ text {No.}\\\ text {Check。}
\\\\\ quad\ text {表达式完全考虑了吗? } &\ text {是。}\\\ quad\ text {乘法。}\\\ begin {array} {l} {4 x^ {4} (x+3)}\\ {4 x^ {4}\\ {4 x^ {5} +12 x^ {4}\ checkmark\ end {array}\ end {数组}\)
完全考虑以下因素:\(3 a^{4}+18 a^{3}\)
- 回答
-
3\(a^{3}(a+6)\)
完全考虑以下因素:\(45 b^{6}+27 b^{5}\)
- 回答
-
9\(b^{5}(5 b+3)\)
完全考虑以下因素:\(12 x^{2}-11 x+2\)
- 回答
-
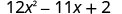
有全球气候基金吗? 不。 它是二项式、三项式还是超过
三个项?三项式。 a 和 c 是完美的正方形吗? 不,a = 12,
不是一个完美的正方形。使用反复试验或 “ac” 方法。
我们将在这里使用反复试验。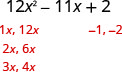
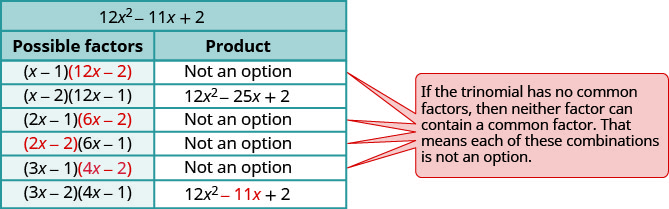
- 查看。 \(\begin{array}{l}{(3 x-2)(4 x-1)} \\ {12 x^{2}-3 x-8 x+2} \\ {12 x^{2}-11 x+2 }\checkmark \end{array}\)
完全考虑以下因素:\(10 a^{2}-17 a+6\)
- 回答
-
\((5 a-6)(2 a-1)\)
完全考虑以下因素:\(8 x^{2}-18 x+9\)
- 回答
-
\((2 x-3)(4 x-3)\)
完全考虑以下因素:\(g^{3}+25 g\)
- 回答
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, g.} &g^{3}+25 g \\\text { Factor out the GCF. } & &g\left(g^{2}+25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \quad \text { Is it a sum? Of squares? } & \text { Yes. } & \text { Sums of squares are prime. } \\\text { Check. } \\ \\ \quad \text { Is the expression factored completely? } &\text { Yes. } \\ \quad \text { Multiply. } \\ \qquad \begin{array}{l}{g\left(g^{2}+25\right)} \\ {g^{3}+25 g }\checkmark \end{array} \end{array}\)
完全考虑以下因素:\(x^{3}+36 x\)
- 回答
-
\(x\left(x^{2}+36\right)\)
完全考虑以下因素:\(27 y^{2}+48\)
- 回答
-
3\(\left(9 y^{2}+16\right)\)
完全考虑以下因素:\(12 y^{2}-75\)
- 回答
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 3.} &12 y^{2}-75 \\\text { Factor out the GCF. } & &3\left(4 y^{2}-25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \text { Is it a sum?} & \text { No. } & \\ \text { Is it a difference? Of squares or cubes? } &\text { Yes, squares. } & 3\left((2 y)^{2}-(5)^{2}\right) \\ \text { Write as a product of conjugates. } & &3(2 y-5)(2 y+5)\\\text { Check. } \\ \\ \text { Is the expression factored completely? } & \text{ Yes.}& \\ \text { Neither binomial is a difference of } \\ \text { squares. } \\ \text{ Multiply.} \\ \quad \begin{array}{l}{3(2 y-5)(2 y+5)} \\ {3\left(4 y^{2}-25\right)} \\ {12 y^{2}-75}\checkmark \end{array} \end{array}\)
完全考虑以下因素:\(16 x^{3}-36 x\)
- 回答
-
4\(x(2 x-3)(2 x+3)\)
完全考虑以下因素:\(27 y^{2}-48\)
- 回答
-
3\((3 y-4)(3 y+4)\)
完全考虑以下因素:\(4 a^{2}-12 a b+9 b^{2}\)
- 回答
-
有全球气候基金吗? 不。 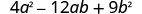
它是二项式、三项式还是
还有其他术语?三项式与\(a\neq 1\). 但是第一个术语是一个
完美的方块。最后一个术语是完美的正方形吗? 是的。 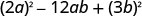
它符合图案\(a^{2}-2 a b+b^{2}\)吗,? 是的。 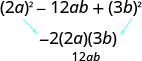
把它写成正方形。 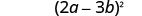
检查你的答案。 这个表达式是完全考虑的吗? 是的。 二项式不是平方差。 乘以。 \((2 a-3 b)^{2}\) \((2 a)^{2}-2 \cdot 2 a \cdot 3 b+(3 b)^{2}\) \(4 a^{2}-12 a b+9 b^{2} \checkmark\)
完全考虑以下因素:\(4 x^{2}+20 x y+25 y^{2}\)
- 回答
-
\((2 x+5 y)^{2}\)
完全考虑以下因素:\(9 m^{2}+42 m n+49 n^{2}\)
- 回答
-
\((3 m+7 n)^{2}\)
完全考虑以下因素:\(6 y^{2}-18 y-60\)
- 回答
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 6.} &6 y^{2}-18 y-60 \\\text { Factor out the GCF. } & \text { Trinomial with leading coefficient } 1&6\left(y^{2}-3 y-10\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more terms? } & & \\ \text { "Undo' FOIL. } & 6(y\qquad )(y\qquad ) &6(y+2)(y-5) \\ \text { Check your answer. } \\ \text { Is the expression factored completely? } & & \text{ Yes.} \\ \text { Neither binomial is a difference of squares. } \\ \text { Multiply. } \\ \\\qquad \begin{array}{l}{6(y+2)(y-5)} \\ {6\left(y^{2}-5 y+2 y-10\right)} \\ {6\left(y^{2}-3 y-10\right)} \\ {6 y^{2}-18 y-60} \checkmark \end{array} \end{array}\)
完全考虑以下因素:\(8 y^{2}+16 y-24\)
- 回答
-
8\((y-1)(y+3)\)
完全考虑以下因素:\(5 u^{2}-15 u-270\)
- 回答
-
5\((u-9)(u+6)\)
完全考虑以下因素:\(24 x^{3}+81\)
- 回答
-
有全球气候基金吗? 是的,3。 \(24 x^{3}+81\) 把它排除在外。 3\(\left(8 x^{3}+27\right)\) 在括号中,它是二项式、三项式
还是超过三个项?二项式。 是总和还是差异? 总和。 正方形还是立方体? 立方体总和。 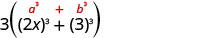
使用立方体总和模式进行编写。 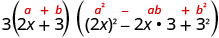
这个表达式是完全考虑的吗? 是的。 3\((2 x+3)\left(4 x^{2}-6 x+9\right)\) 乘法检查。 我们把支票留给你。
完全考虑以下因素:\(250 m^{3}+432\)
- 回答
-
2\((5 m+6)\left(25 m^{2}-30 m+36\right)\)
完全考虑以下因素:\(81 q^{3}+192\)
- 回答
-
\(3(3q+4)\left(9q^{2}-12 q+16\right)\)
完全考虑以下因素:\(2 x^{4}-32\)
- 回答
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &2 x^{4}-32 \\\text { Factor out the GCF. } & &2\left(x^{4}-16\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } & \text { Binomial. }& \\ \text { Is it a sum or difference? } &\text { Yes. }& \\\text { Of squares or cubes? } & \text { Difference of squares. } & 2\left(\left(x^{2}\right)^{2}-(4)^{2}\right) \\ \text { Write it as a product of conjugates. } & & 2\left(x^{2}-4\right)\left(x^{2}+4\right) \\ \text { The first binomial is again a difference of squares. } & & 2\left((x)^{2}-(2)^{2}\right)\left(x^{2}+4\right) \\ \text { Write it as a product of conjugates. } & & 2(x-2)(x+2)\left(x^{2}+4\right) \\ \text { Is the expression factored completely? } &\text { Yes. } & \\ \\ \text { None of these binomials is a difference of squares. } \\ \text { Check your answer. } \\ \text{ Multiply. }\\ \\ \qquad \qquad \begin{array}{l}{2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-10)} \\ {2 x^{4}-32} \checkmark \end{array} \end{array}\)
完全考虑以下因素:\(4 a^{4}-64\)
- 回答
-
4\(\left(a^{2}+4\right)(a-2)(a+2)\)
完全考虑以下因素:\(7 y^{4}-7\)
- 回答
-
7\(\left(y^{2}+1\right)(y-1)(y+1)\)
完全考虑以下因素:\(3 x^{2}+6 b x-3 a x-6 a b\)
- 回答
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 3.} &3 x^{2}+6 b x-3 a x-6 a b\\\text { Factor out the GCF. } & &3\left(x^{2}+2 b x-a x-2 a b\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { More than } 3 & \\ \text { or are there more terms? } &\text { terms. } & \\ \text { Use grouping. } & & \begin{array}{c}{3[x(x+2 b)-a(x+2 b)]} \\ {3(x+2 b)(x-a)}\end{array} \\ \text { Check your answer. } \\ \\ \text { Is the expression factored completely? Yes. } \\ \text { Multiply. } \\\qquad \qquad \begin{array}{l}{3(x+2 b)(x-a)} \\ {3\left(x^{2}-a x+2 b x-2 a b\right)} \\ {3 x^{2}-3 a x+6 b x-6 a b} \checkmark \end{array}\end{array}\)
完全考虑以下因素:\(6 x^{2}-12 x c+6 b x-12 b c\)
- 回答
-
6\((x+b)(x-2 c)\)
完全考虑以下因素:\(16 x^{2}+24 x y-4 x-6 y\)
- 回答
-
2\((4 x-1)(x+3 y)\)
完全考虑以下因素:\(10 x^{2}-34 x-24\)
- 回答
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &10 x^{2}-34 x-24\\\text { Factor out the GCF. } & &2\left(5 x^{2}-17 x-12\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { Trinomial with } & \\ \text { or are there more than three terms? } &\space a \neq 1 & \\ \text { Use trial and error or the "ac" method. } & & 2\left(5 x^{2}-17 x-12\right) \\ & & 2(5 x+3)(x-4) \\ \text { Check your answer. Is the expression factored } \\\text { completely? Yes. }\\ \\ \text { Multiply. } \\ \qquad \begin{array}{l}{2(5 x+3)(x-4)} \\ {2\left(5 x^{2}-20 x+3 x-12\right)} \\ {2\left(5 x^{2}-17 x-12\right)} \\ {10 x^{2}-34 x-24}\checkmark \end{array}\end{array}\)
完全考虑以下因素:\(4 p^{2}-16 p+12\)
- 回答
-
4\((p-1)(p-3)\)
完全考虑以下因素:\(6 q^{2}-9 q-6\)
- 回答
-
3\((q-2)(2 q+1)\)
关键概念
- 分解多项式的通用策略见图\(\PageIndex{1}\)。
- 如何分解多项式
- 有最大的共同因素吗? 把它排除在外。
- 多项式是二项式、三项式还是超过三个项?
- 如果是二项式:
是总和吗?- 正方形? 平方和不分解。
- 多维数据集? 使用立方体总和模式。
- 正方形? 因子是共轭物的乘积。
- 多维数据集? 使用立方体差异图案。
- 如果是三项式:
是这样的\(x^{2}+b x+c\)吗? 撤消 FOIL。
是这样的吗\(a x^{2}+b x+c\)?- 如果 'a' 和 'c' 是正方形,请检查它是否符合三项式方形图案。
- 使用反复试验或 “ac” 方法。
- 如果它有三个以上的术语:
使用分组方法。
- 如果是二项式:
- 查看。 完全考虑了吗? 这些因子会乘回原来的多项式吗?


