7.4: 因子特殊产品
- Page ID
- 204556
在本节结束时,您将能够:
- 因子完美正方形三项式
- 正方形的因子差
- 因子总和和和与立方差
- 选择完全分解多项式的方法
我们在上一节中开发的分解策略将指导您分解大多数具有三个以上项的二项式、三项式和多项式。 我们已经看到,一些二项式和三项式是由特殊乘积产生的,即二项式的平方和乘法共轭物。 如果你学会识别这类多项式,你可以使用特殊乘积模式更快地分解它们。
Factor Perfect Square 三项式
有些三项式是完美的正方形。 它们是将二项式乘以本身得出的。 你可以使用 FOIL 对二项式进行平方,但是使用你在上一章中看到的二项式方块模式可以节省一个步骤。 让我们通过使用 FOIL 对二项式求平方来回顾二项式方格模式。
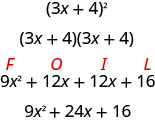
第一个项是二项式第一个项的平方,最后一个项是最后一个项的平方。 中间项是二项式两个项的乘积的两倍。
\[\begin{array}{c}{(3 x)^{2}+2(3 x \cdot 4)+4^{2}} \\ {9 x^{2}+24 x+16}\end{array}\]
三项式\(9 x^{2}+24+16\)被称为完美正方形三项式。 它是二项式 3 x +4 的平方。
我们将在这里重复二项式方块模式,用作因式分解的参考。
如果 a 和 b 是实数,
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \qquad(a-b)^{2}=a^{2}-2 a b+b^{2}\]
当你对二项式求平方时,乘积是一个完美的方形三项式。 在本章中,你正在学习分解——现在,你将从一个完美的正方三项式开始,然后将其分解为其素因子。
你可以使用上一节中描述的方法来分解这个三项式,因为它的形式是这样的\(ax^{2}+bx+c\)。 但是,如果你认识到第一个和最后一个项是正方形,而三项式符合完美的方形三项式模式,那么你可以为自己节省很多工作。
这是图案——与二项式方块图案相反。
如果 a 和 b 是实数,
\[a^{2}+2 a b+b^{2}=(a+b)^{2} \qquad a^{2}-2 a b+b^{2}=(a-b)^{2}\]
要使用这种模式,你必须认识到给定的三项式适合它。 首先检查前导系数是否为完美正方形\(a^2\)。 接下来检查最后一个术语是否是完美的正方形,\(b^2\)。 然后看看中间词——是产品的两倍\(2ab\)吗? 如果一切正常,你可以很容易地写出因子。
因子:\(9 x^{2}+12 x+4\)
- 回答
-



因子:\(4 x^{2}+12 x+9\)
- 回答
-
\((2 x+3)^{2}\)
因子:\(9 y^{2}+24 y+16\)
- 回答
-
\((3 y+4)^{2}\)
中间术语的符号决定我们将使用哪种模式。 当中间术语为负数时,我们使用模式\(a^{2}-2 a b+b^{2}\),其因素是\((a-b)^{2}\)。
此处总结了这些步骤。
F@@
\(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
我们现在要研究一个中间词为负值的地方。
因子:\(81 y^{2}-72 y+16\)
- 回答
-
第一个和最后一个项是平方。 看看中间术语是否符合完美方形三项式的模式。 中间项是负数,所以二项式平方是负数\((a-b)^{2}\)。
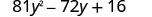
第一个和最后一个项是完美的正方形吗? 
查看中间术语。 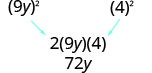
是否匹配\((a-b)^{2}\)? 是的。 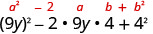
写下二项式的平方。 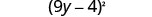
乘法检查。 \((9 y-4)^{2}\) \((9 y)^{2}-2 \cdot 9 y \cdot 4+4^{2}\) \(81 y^{2}-72 y+16 \checkmark\)
因子:\(64 y^{2}-80 y+25\)
- 回答
-
\((8 y-5)^{2}\)
因子:\(16 z^{2}-72 z+81\)
- 回答
-
\((4 z-9)^{2}\)
下一个例子将是具有两个变量的完美平方三项式。
因子:\(36 x^{2}+84 x y+49 y^{2}\)
- 回答
-
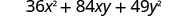
测试每个术语以验证模式。 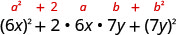
因子。 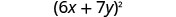
乘法检查。 \((6 x+7 y)^{2}\) \((6 x)^{2}+2 \cdot 6 x \cdot 7 y+(7 y)^{2}\) \(36 x^{2}+84 x y+49 y^{2} \checkmark\)
因子:\(49 x^{2}+84 x y+36 y^{2}\)
- 回答
-
\((7 x+6 y)^{2}\)
因子:\(64 m^{2}+112 m n+49 n^{2}\)
- 回答
-
\((8 m+7 n)^{2}\)
因子:\(9 x^{2}+50 x+25\)
- 回答
-
\(\begin{array}{lc} & 9 x^{2}+50 x+25 \\ \text { Are the first and last terms perfect squares? } & (3 x)^{2} \qquad\quad (5)^2 \\ \text { Check the middle term-is it 2ab? } & (3 x)^{2} \searrow_{2(3 x)(5) }\swarrow (5)^{2}. \\ & \tiny{30x} \\ \text { No! } 30 x \neq 50 x & \text { This does not fit the pattern! } \\ \text { Factor using the "ac" method. } & 9 x^{2}+50 x+25 \\ \begin{array}{c}{\text { ac }} \\ {\text { Notice: } 9 \cdot 25 \text { and } 5 \cdot 45=225} \\ {225}\end{array} \\ {\text { Split the middle term. }} & \begin{array}{c}{9 x^{2}+5 x+45 x+25} \\ {x(9 x+5)+5(9 x+5)} \\ {(9 x+5)(x+5)}\end{array}\\ {\text { Factor by grouping. }} \\ \text { Check. } & \\ \begin{array}{l}{(9 x+5)(x+5)} \\ {9 x^{2}+45 x+5 x+25} \\ {9 x^{2}+50 x+25}\checkmark\end{array}\end{array}\)
因子:\(16 r^{2}+30 r s+9 s^{2}\)
- 回答
-
\((8 r+3 s)(2 r+3 s)\)
因子:\(9 u^{2}+87 u+100\)
- 回答
-
\((3 u+4)(3 u+25)\)
还记得我们的多项式分解策略的第一步吗? 这是在问 “有最大的共同因素吗?” 而且,如果有的话,你可以在进一步研究之前考虑GCF。 完美方三项式可能在所有三个项中都有 GCF,应该先将其分解出来。 而且,有时候,一旦考虑了 GCF,你就会认出一个完美的方形三项式。
因子:\(36 x^{2} y-48 x y+16 y\)
- 回答
-
\(36 x^{2} y-48 x y+16 y\) 有全球气候基金吗? 是的,4 y,所以把它排除在外。 4\(y\left(9 x^{2}-12 x+4\right)\) 这是一个完美的方形三项式吗? 验证图案。 
因子。 4\(y(3 x-2)^{2}\) 记住:在最终产品中保留因子 4 y。 查看。 \(4y(3 x-2)^{2}\) \(4y[(3 x)^{2}-2 \cdot 3 x \cdot 2+2^{2}]\) \(4 y(9 x)^{2}-12 x+4\) \(36 x^{2} y-48 x y+16 y\checkmark\)
因子:\(8 x^{2} y-24 x y+18 y\)
- 回答
-
2\(y(2 x-3)^{2}\)
因子:\(27 p^{2} q+90 p q+75 q\)
- 回答
-
3\(q(3 p+5)^{2}\)
正方形的因子差
你在之前看到的另一个特殊产品是 “共轭物产物” 图案。 你用它来乘以两个作为共轭物的二项式。 下面是一个例子:
\[\begin{array}{c}{(3 x-4)(3 x+4)} \\ {9 x^{2}-16}\end{array}\]
请记住,当你乘以共轭二项式时,乘积的中间项加起来为 0。 你剩下的只是一个二项式,即平方差。
乘以共轭物是从两个二项式的乘积获得二项式的唯一方法。
如果 a 和 b 是实数
\[(a-b)(a+b)=a^{2}-b^{2}\]
该乘积称为平方差。
为了分数,我们将使用 “反向” 乘积模式来分解平方差。 平方因子与共轭物乘积的差。
如果 a 和 b 是实数,
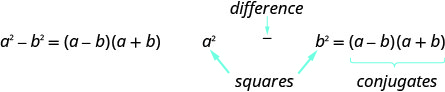
请记住,“差异” 是指减法。 因此,要使用这种模式,你必须确保你有一个二项式,其中要减去两个正方形。
因子:\(x^{2}-4\)
- 回答
-




因子:\(h^{2}-81\)
- 回答
-
\((h-9)(h+9)\)
因子:\(k^{2}-121\)
- 回答
-
\((k-11)(k+11)\)
\(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
重要的是要记住,平方和不会分解为二项式的乘积。 没有二项式因子可以相乘得出平方和。 移除任何 GCF 后,表达式\(a^{2}+b^{2}\)为 prime!
别忘了 1 是一个完美的正方形。 在下一个例子中,我们需要使用这个事实。
因子:\(64 y^{2}-1\)
- 回答
-
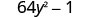
这是区别吗? 是的。 
第一个和最后一个项是完美的正方形吗? 是的-把它们写成正方形。 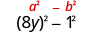
因子是共轭物的乘积。 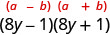
乘法检查。 \((8 y-1)(8 y+1)\) \(64 y^{2}-1 \checkmark\)
因子:\(m^{2}-1\)
- 回答
-
\((m-1)(m+1)\)
因子:\(81 y^{2}-1\)
- 回答
-
\((9 y-1)(9 y+1)\)
因子:\(121 x^{2}-49 y^{2}\)
- 回答
-
\(\begin{array}{lc} & 121 x^{2}-49 y^{2} \\ \text { Is this a difference of squares? Yes. } & (11 x)^{2}-(7 y)^{2} \\ \text { Factor as the product of conjugates. } & (11 x-7 y)(11 x+7 y) \\ \text { Check by multiplying. } & \\ \begin{array}{l}{(11 x-7 y)(11 x+7 y)} \\ {121 x^{2}-49 y^{2}} \checkmark \end{array} \end{array}\)
因子:\(196 m^{2}-25 n^{2}\)
- 回答
-
\((16 m-5 n)(16 m+5 n)\)
因子:\(144 p^{2}-9 q^{2}\)
- 回答
-
\((12 p-3 q)(12 p+3 q)\)
下一个例子中的二项式可能是 “向后看”,但它仍然是平方差。
因子:\(100-h^{2}\)
- 回答
-
\(\begin{array}{lc} & 100-h^{2} \\ \text { Is this a difference of squares? Yes. } & (10)^{2}-(h)^{2}\\ \text { Factor as the product of conjugates. } & (10-h)(10+h)\\ \text { Check by multiplying. } & \\ \begin{array}{l}{(10-h)(10+h)} \\ {100-h^{2}} \checkmark \end{array} \end{array}\)
注意不要将原始表达式重写为\(h^{2}-100\)。
自己考虑因素\(h^{2}-100\),然后注意结果与之有何不同\((10-h)(10+h)\)。
因子:\(144-x^{2}\)
- 回答
-
\((12-x)(12+x)\)
因子:\(169-p^{2}\)
- 回答
-
\((13-p)(13+p)\)
为了在下一个示例中完全分解二项式,我们将对平方差进行两次分解!
因子:\(x^{4}-y^{4}\)
- 回答
-
\(\begin{array}{lc}\text { Is this a difference of squares? Yes. } & {x^{4}-y^{4}} \\\text { Factor it as the product of conjugates. } & {\left(x^{2}\right)^{2}-\left(y^{2}\right)^{2}} \\ \text { Notice the first binomial is also a difference of squares! } & {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ \text { Factor it as the product of conjugates. The last }& {(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ \text { factor, the sum of squares, cannot be factored. } \\ \\ \text { Check by multiplying. } & \\\begin{array}{l}{(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ {[(x-y)(x+y)]\left(x^{2}+y^{2}\right)} \\ {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ {x^{4}-y^{4}} \checkmark \end{array} \end{array}\)
因子:\(a^{4}-b^{4}\)
- 回答
-
\(\left(a^{2}+b^{2}\right)(a+b)(a-b)\)
因子:\(x^{4}-16\)
- 回答
-
\(\left(x^{2}+4\right)(x+2)(x-2)\)
与往常一样,每当你有要因子的表达式时,你都应该先寻找一个共同因子。 有时候,一个共同因子可能 “掩盖” 平方差,在你将 GCF 分解出来之前,你无法识别出完美的正方形。
因子:\(8 x^{2} y-98 y\)
- 回答
-
\(\begin{array}{lc}& 8 x^{2} y-98 y \\ \text { Is there a GCF? Yes, } 2 y-\text { factor it out! } & 2 y\left(4 x^{2}-49\right) \\ \text { Is the binomial a difference of squares? Yes. } & 2 y\left((2 x)^{2}-(7)^{2}\right) \\ \text { Factor as a product of conjugates. } & 2 y(2 x-7)(2 x+7) \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{2 y(2 x-7)(2 x+7)} \\ {2 y[(2 x-7)(2 x+7)]} \\ {2 y\left(4 x^{2}-49\right)} \\ {8 x^{2} y-98 y} \checkmark \end{array} \end{array}\)
因子:\(7 x y^{2}-175 x\)
- 回答
-
7\(x(y-5)(y+5)\)
因子:\(45 a^{2} b-80 b\)
- 回答
-
5\(b(3 a-4)(3 a+4)\)
因子:\(6 x^{2}+96\)
- 回答
-
\(\begin{array}{lc}&6 x^{2}+96 \\ \text { Is there a GCF? Yes, } 6-\text { factor it out! } & 6\left(x^{2}+16\right) \\ \text { Is the binomial a difference of squares? No, it } & \\ \text { is a sum of squares. Sums of squares do not factor! } & \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{6\left(x^{2}+16\right)} \\ {6 x^{2}+96 }\checkmark \end{array} \end{array}\)
因子:\(8 a^{2}+200\)
- 回答
-
8\(\left(a^{2}+25\right)\)
因子:\(36 y^{2}+81\)
- 回答
-
9\(\left(4 y^{2}+9\right)\)
多维数据集的因子总和和和和差
还有另一种特殊的分解模式,我们在乘以多项式时没有使用这种模式。 这是立方体总和和和差的模式。 我们将先写出这些公式,然后通过乘法检查它们。
\[\begin{aligned} a^{3}+b^{3} &=(a+b)\left(a^{2}-a b+b^{2}\right) \\ a^{3}-b^{3} &=(a-b)\left(a^{2}+a b+b^{2}\right) \end{aligned}\]
我们将检查第一个图案,然后将第二个模式留给你。
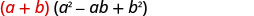 |
|
| 分发。 |  |
| 乘。 | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| 将相似的术语组合在一起。 | \(a^{3}+b^{3}\) |
\[\begin{array}{l}{a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)} \\ {a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)}\end{array}\]
这两种模式看起来很相似,不是吗? 但是请注意这些因素中的迹象。 二项式因子的符号与原始二项式中的符号相匹配。 而三项式因子的中间项的符号与原始二项式中的符号相反。 如果你认出标志的图案,它可能会帮助你记住这些图案。

无法考虑立方体总和差值模式中的三项式因子。
如果你学会识别 1 到 10 的整数的立方体,就像你学会识别正方形一样,这会非常有帮助。 我们在图中列出了从 1 到 10 的整数的立方体\(\PageIndex{1}\)。

因子:\(x^{3}+64\)
- 回答
-





因子:\(x^{3}+27\)
- 回答
-
\((x+3)\left(x^{2}-3 x+9\right)\)
因子:\(y^{3}+8\)
- 回答
-
\((y+2)\left(y^{2}-2 y+4\right)\)
要计算立方体的总和或差值,请执行以下操作:
- 二项式是否符合立方体模式的总和或差异?
- 是总和还是差异?
- 第一个和最后一个学期是完美的立方体吗?
- 把它们写成立方体。
- 使用立方体的总和或差值模式。
- 在圆括号内简化
- 通过乘以因子进行检查。
因子:\(: x^{3}-1000\)
- 回答
-

这个二项式是区别的。 第一个和最后一个术语是完美的立方体。 将术语写成立方体。 
使用立方体差异图案。 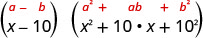
简化。 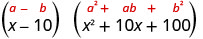
乘法检查。 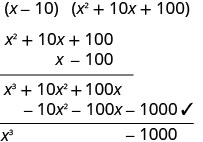
因子:\(u^{3}-125\)
- 回答
-
\((u-5)\left(u^{2}+5 u+25\right)\)
因子:\(v^{3}-343\)
- 回答
-
\((v-7)\left(v^{2}+7 v+49\right)\)
注意在立方体总和和差值的因子中使用正确的符号。
因子:\(512-125 p^{3}\)
- 回答
-

这个二项式是区别的。 第一个和最后一个术语是完美的立方体。 将术语写成立方体。 
使用立方体差异图案。 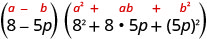
简化。 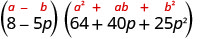
乘法检查。 我们会把支票留给你。
因子:\(64-27 x^{3}\)
- 回答
-
\((4-3 x)\left(16+12 x+9 x^{2}\right)\)
因子:\(27-8 y^{3}\)
- 回答
-
\((3-2 y)\left(9+6 y+4 y^{2}\right)\)
因子:\(27 u^{3}-125 v^{3}\)
- 回答
-

这个二项式是区别的。 第一个和最后一个术语是完美的立方体。 将术语写成立方体。 
使用立方体差异图案。 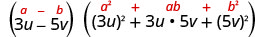
简化。 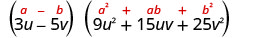
乘法检查。 我们会把支票留给你。
因子:\(8 x^{3}-27 y^{3}\)
- 回答
-
\((2 x-3 y)\left(4 x^{2}+6 x y+9 y^{2}\right)\)
因子:\(1000 m^{3}-125 n^{3}\)
- 回答
-
\((10 m-5 n)\left(100 m^{2}+50 m n+25 n^{2}\right)\)
在下一个例子中,我们首先考虑了 GCF。 然后我们就可以识别出立方体的总和了。
因子:\(5 m^{3}+40 n^{3}\)
- 回答
-
查看。 要检查一下,你可能会发现先将立方体因子的总和相乘,然后将该乘积乘以 5 会更容易。 我们将把乘法留给你。
将共同因素考虑在内。 
这个二项式是一个总和。 第一个和最后一个术语是完美的立方体。 将术语写成立方体。 
使用立方体总和模式。 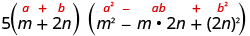
简化。 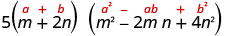
- 5\((m+2 n)\left(m^{2}-2 m n+4 n^{2}\right)\)
因子:\(500 p^{3}+4 q^{3}\)
- 回答
-
4\((5 p+q)\left(25 p^{2}-5 p q+q^{2}\right)\)
因子:\(432 c^{3}+686 d^{3}\)
- 回答
-
2\((6 c+7 d)\left(36 c^{2}-42 c d+49 d^{2}\right)\)
关键概念
- 因子完美平方三项式参见示例。 \(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
- 平方的因子差参见示例。 \(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
- 系数立方体的总和和与差分要分解立方体的总和或差值:参见示例。
- 二项式是否符合立方体模式的总和或差异? 是总和还是差异? 第一个和最后一个学期是完美的立方体吗?
- 把它们写成立方体。
- 使用立方体的总和或差值模式。
- 在圆括号内简化
- 通过乘以因子进行检查。
词汇表
- 完美的方形三项式图案
- 如果 a 和 b 是实数,
\[\begin{array}{cc} {a^2+2ab+b^2=(a+b)^2}&{a^2−2ab+b^2=(a−b)^2}\\ \nonumber \end{array}\]
- 正方差图案
- 如果 a 和 b 是实数,

- 立方体总和差值模式
-
\[\begin{array}{cc} {a^3+b^3=(a+b)(a^2−ab+b^2)}&{a^3−b^3=(a−b)(a^2+ab+b^2)}\\ \nonumber \end{array}\]


