Skip to main content
Global

6.2：使用指数的乘法属性

  1. Last updated
  2. Save as PDF
  • Page ID
    204954

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 使用指数简化表达式
    • 使用指数的乘积属性简化表达式
    • 使用指数的幂属性简化表达式
    • 使用 Product to a Power 属性简化表达式
    • 通过应用多个属性来简化表达式
    • 乘以单项式
    注意

    在开始之前，请参加这个准备测验。

    1. 简化：\(\frac{3}{4}\cdot \frac{3}{4}\)
      如果您错过了此问题，请查看练习 1.6.13。
    2. 简化：\((−2)(−2)(−2)\)。
      如果您错过了此问题，请查看练习 1.5.13。

    使用指数简化表达式

    请记住，指数表示相同数量的重复乘法。 例如，\(2^4\)表示\(4\)因子的乘积\(2\)，因此\(2^4\)均值\(2·2·2·2\)。

    让我们回顾一下带有指数的表达式的词汇表。

    指数表示法

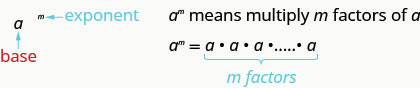
    此图有两列。 左列中是 a 到 m 的幂次方。 m 以蓝色标记为指数。 a 以红色标记为基础。 右栏是文本 “a 到 m 的幂次方表示乘以 a 的 m 个因子”。 在此之下是 a 到 m 的乘以 a 乘以 a，然后是省略号，下面是蓝色的 “m 因子”。

    这已经被大\(a\)\(m^{th}\)力读懂了。

    在表达式中\(a^{m}\)，指数\(m\)告诉我们使用基数 a 作为因子的次数。

    此图有两列。 左列包含 4 个立方体。 下面是4乘以4乘以4，下面用蓝色写的 “3 个因子”。 右列包含负9到第五次方。 下方是负9乘以负9乘以负9乘以负9乘以负9乘以负9，下面用蓝色写的 “5 个因子”。

    在我们开始处理包含指数的变量表达式之前，让我们简化几个仅涉及数字的表达式。

    示例\(\PageIndex{1}\)

    简化：

    1. \(4^{3}\)
    2. \(7^{1}\)
    3. \(\left(\frac{5}{6}\right)^{2}\)
    4. \((0.63)^{2}\)
    回答
    1. \(\begin{array}{ll} & 4^{3}\\ {\text { Multiply three factors of } 4 .} & {4 \cdot 4 \cdot 4} \\ {\text { Simplify. }} & {64}\end{array}\)
    2. \(\begin{array}{ll} & 7^{1}\\ \text{Multiply one factor of 7.} & 7\end{array}\)
    3. \(\begin{array}{ll} &\left(\frac{5}{6}\right)^{2}\\ {\text { Multiply two factors. }} & {\left(\frac{5}{6}\right)\left(\frac{5}{6}\right)} \\ {\text { Simplify. }} & {\frac{25}{36}}\end{array}\)
    4. \(\begin{array}{ll} &(0.63)^{2}\\ {\text { Multiply two factors. }} & {(0.63)(0.63)} \\ {\text { Simplify. }} & {0.3969}\end{array}\)
    示例\(\PageIndex{2}\)

    简化：

    1. \(6^{3}\)
    2. \(15^{1}\)
    3. \(\left(\frac{3}{7}\right)^{2}\)
    4. \((0.43)^{2}\)
    回答
    1. 216
    2. 15
    3. \(\frac{9}{49}\)
    4. 0.1849
    示例\(\PageIndex{3}\)

    简化：

    1. \(2^{5}\)
    2. \(21^{1}\)
    3. \(\left(\frac{2}{5}\right)^{3}\)
    4. \((0.218)^{2}\)
    回答
    1. 32
    2. 21
    3. \(\frac{8}{125}\)
    4. 0.047524
    示例\(\PageIndex{4}\)

    简化：

    1. \((-5)^{4}\)
    2. \(-5^{4}\)
    回答
    1. \(\begin{array}{ll} &(-5)^{4}\\{\text { Multiply four factors of }-5} & {(-5)(-5)(-5)} \\ {\text { Simplify. }} & {625}\end{array}\)
    2. \(\begin{array}{ll} &-5^{4}\\{\text { Multiply four factors of } 5 .} & {-(5 \cdot 5 \cdot 5 \cdot 5)} \\ {\text { Simplify. }} & {-625}\end{array}\)

    请注意示例 1 和示例第 2\(\PageIndex{4}\)\(\PageIndex{4}\) 部分中的相似之处和不同之处！ 为什么答案不同？ 当我们遵循第 1 部分中的运算顺序时，圆括号告诉我们要将次数提高\((−5)\)到第 4 次方。 在第 2 部分中，我们只将第 4 次功率提高\(5\)到第 4 次方，然后取相反的次方。

    示例\(\PageIndex{5}\)

    简化：

    1. \((-3)^{4}\)
    2. \(-3^{4}\)
    回答
    1. 81
    2. −81
    示例\(\PageIndex{6}\)

    简化：

    1. \((-13)^{4}\)
    2. \(-13^{4}\)
    回答
    1. 169
    2. −169

    使用指数的乘积属性简化表达式

    你已经看到，当你通过加减来组合相似的项时，你需要有相同的基数和相同的指数。 但是当你乘以和除法时，指数可能会有所不同，有时基数也可能不同。

    我们将通过在几个示例中寻找模式来推导指数的属性。

    首先，我们将看一个通向产品属性的示例。

      x 平方乘以 x 立方体。
    这是什么意思？
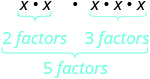    总共有多少因素？    		 x 乘以 x，乘以 x 乘以 x x 有两个因子。x 倍 x 乘以 x 有三个因子。2 加 3 是五个因子。
    所以，我们有 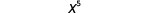x 到第五次方。
    请注意，5 是指数 2 和 3 的总和。 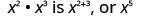x 平方乘以 x cubed 等于 2 加 3 的幂次方，或 x 到第五次方。

    我们写道：\[\begin{array}{c}{x^{2} \cdot x^{3}} \\ {x^{2+3}} \\ {x^{5}}\end{array}\]

    基数保持不变，我们添加了指数。 这导致了指数的乘积属性。

    指数的乘积属性

    如果\(a\)是实数，并且\(m\)和\(n\)正在计算数字，那么

    \[a^{m} \cdot a^{n}=a^{m+n}\]

    要用相似的基数相乘，请将指数相加。

    带数字的示例有助于验证此属性。

    \[\begin{array}{rll} {2^3\cdot2^2} &\stackrel{?}{=} & 2^{2+3}\\ {4\cdot 8} &\stackrel{?}{=} & 2^{5} \\ {32} &=& 32\checkmark\end{array}\]

    示例\(\PageIndex{7}\)

    简化：\(y^{5} \cdot y^{6}\)

    回答
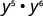
      y 到第五次幂乘以 y 到第六次方。
    使用产品属性\(a^{m} \cdot a^{n}=a^{m+n}\)。 y 以 5 加 6 的幂计算。
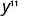
    简化。 y 到第十一个次方。
    示例\(\PageIndex{8}\)

    简化：\(b^{9} \cdot b^{8}\)

    回答

    \(b^{17}\)

    示例\(\PageIndex{9}\)

    简化：\(x^{12} \cdot x^{4}\)

    回答

    \(x^{16}\)

    示例\(\PageIndex{10}\)

    简化：

    1. \(2^{5} \cdot 2^{9}\)
    2. \(3\cdot 3^{4}\)
    回答

    一个。

      2 到第五次乘以 2 到第九次方。
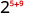
    使用产品属性\(a^{m} \cdot a^{n}=a^{m+n}\)。 2 以 5 加 9 的次方。
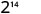
    简化。 2 到第 14 次的力量。

    b。

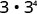
      3 到第五次功率乘以 3 到第四次方。
    使用产品属性\(a^{m} \cdot a^{n}=a^{m+n}\)。 3 以 5 加 4 的次方。
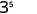
    简化。 3 到第九次方。
    示例\(\PageIndex{11}\)

    简化：

    1. \(5\cdot 5^{5}\)
    2. \(4^{9} \cdot 4^{9}\)
    回答
    1. \(5^{6}\)
    2. \(4^{18}\)
    示例\(\PageIndex{12}\)

    简化：

    1. \(7^{6} \cdot 7^{8}\)
    2. \(10 \cdot 10^{10}\)
    回答
    1. \(7^{14}\)
    2. \(10^{11}\)
    示例\(\PageIndex{13}\)

    简化：

    1. \(a^{7} \cdot a\)
    2. \(x^{27} \cdot x^{13}\)
    回答

    一个。

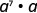
      a 到第七次功率乘以 a。
    重写，\(a = a^1\) a 到第七次幂乘以 a 到第一次方。
    使用产品属性\(a^m\cdot a^n = a^{m+n}\)。 a 以 7 加 1 的幂计算。
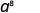
    简化。 a 到第八次方。

    b。

      x 到第二十七次幂乘以 x 到第十三次方。
    注意，基数是相同的，所以加上指数。 x 为 27 加 13 的幂次方。
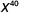
    简化。 x 到第四十次方。
    示例\(\PageIndex{14}\)

    简化：

    1. \(p^{5} \cdot p\)
    2. \(y^{14} \cdot y^{29}\)
    回答
    1. \(p^{6}\)
    2. \(y^{43}\)
    示例\(\PageIndex{15}\)

    简化：

    1. \(z \cdot z^{7}\)
    2. \(b^{15} \cdot b^{34}\)
    回答
    1. \(z^{8}\)
    2. \(b^{49}\)

    我们可以将指数的乘积属性扩展到两个以上的因子。

    示例\(\PageIndex{16}\)

    简化：\(d^{4} \cdot d^{5} \cdot d^{2}\)

    回答
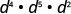
      d 到第四次功率乘以 d 到第五次功率乘以 d 的平方。
    将指数相加，因为基数是相同的。 d 以 4 加 5 加 2 的幂计算。
    简化。 d 到第十一个次方。
    示例\(\PageIndex{17}\)

    简化：\(x^{6} \cdot x^{4} \cdot x^{8}\)

    回答

    \(x^{18}\)

    示例\(\PageIndex{18}\)

    简化：\(b^{5} \cdot b^{9} \cdot b^{5}\)

    回答

    \(b^{19}\)

    使用指数的幂属性简化表达式

    现在让我们来看一个指数表达式，它包含一个上升为幂的乘方。 看看你能不能找到一般财产。

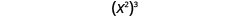      x 平方，括号中，立方体。
    这是什么意思？
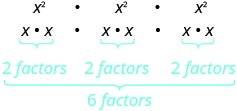    总共有多少因素？    		 x 平方等于 x 平方乘以 x 平方乘以 x 平方，即 x 乘以 x，乘以 x，乘以 x，乘以 x 乘以 x 乘以 x。x 乘以 x 有两个因子。 二加二加二是六个因素。
    所以我们有 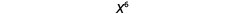x 到第六次方。
    请注意，6 是指数 2 和 3 的乘积。 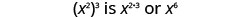x 平方的立方是 x 到 2 倍 3 的次方，或 x 到第六次方。

    我们写道：

    \[\begin{array}{c}{\left(x^{2}\right)^{3}} \\ {x^{2 \cdot 3}} \\ {x^{6}}\end{array}\]

    我们将指数相乘。 这就产生了指数的幂属性。

    指数的幂属性

    如果\(a\)是实数，并且\(m\)和\(n\)是整数，那么

    \[\left(a^{m}\right)^{n}=a^{m \cdot n}\]

    要将乘方提高到乘方，请将指数相乘。

    带数字的示例有助于验证此属性。

    \[\begin{array} {lll} \left(3^{2}\right)^{3} &\stackrel{?}{=}&3^{2 \cdot 3} \\(9)^{3} &\stackrel{?}{=} & 3^{6} \\ 729 &=&729\checkmark \end{array}\]

    示例\(\PageIndex{19}\)

    简化：

    1. \(\left(y^{5}\right)^{9}\)
    2. \(\left(4^{4}\right)^{7}\)
    回答

    一个。

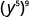
      y 到括号中的第五次方，到第九次方。
    使用电源属性，\(\big(a^m\big)^n = a^{m\cdot n}\)。 y 为 5 倍 9 的次方。
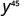
    简化。 y 到第 45 次方。

    b。

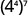
      4 到括号中的第四次方，到第 7 次方。
    使用 power 属性。 4 到 4 次的次方 7。
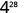
    简化。 4 到第二十八次方。
    示例\(\PageIndex{20}\)

    简化：

    1. \( \left(b^{7}\right)^{5} \)
    2. \(\left(5^{4}\right)^{3}\)
    回答
    1. \( b^{35}\)
    2. \(5^{12}\)
    示例\(\PageIndex{21}\)

    简化：

    1. \(\left(z^{6}\right)^{9}\)
    2. \(\left(3^{7}\right)^{7}\)
    回答
    1. \(z^{54}\)
    2. \(3^{49}\)

    使用乘积到幂属性简化表达式

    现在，我们将看一个包含乘积的表达式，该表达式被提升为幂的乘积。 你能找到这个图案吗？

    \(\begin{array}{ll}{\text { What does this mean? }} & {\text { (2x) }^{3}} \\ {\text { We group the like factors together. }} & {2 x \cdot 2 x \cdot 2 x} \\ {\text { How many factors of } 2 \text { and of } x ?} & {2 \cdot 2 \cdot x^{3}} \\ {\text { Notice that each factor was raised to the power and }(2 x)^{3} \text { is } 2^{3} \cdot x^{3}}\end{array}\)

    \(\begin{array}{ll}\text{We write:} & {(2 x)^{3}} \\ & {2^{3} \cdot x^{3}}\end{array}\)

    指数适用于每个因子！ 这会使乘积成为指数的幂属性。

    指数的乘积与幂属性

    如果\(a\)和\(b\)是实数并且\(m\)是整数，那么

    \[(a b)^{m}=a^{m} b^{m}\]

    要将乘积提高到一个功率，请将每个因子提高到该功率。

    带数字的示例有助于验证此属性：

    \ [\ begin {array} {ll} (2\ cdot 3) ^ {2} &\ stackrel {？} {=} &2^ {2}\ cdot 3^ {2}\\ 6^ {2} &\ stackrel {？} {=} &4\ cdot 9\\ 36 &=&36
    \ 复选标记\ end {array}\]

    示例\(\PageIndex{22}\)

    简化：

    1. \((-9 d)^{2}\)
    2. \((3mn)^{3}\)。
    回答

    一个。

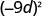
      负 9 d 平方。
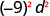
    使用产品属性的力量，\((ab)^m=a^m b^m\)。 负 9 平方 d 的平方。
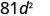
    简化。 81 d 平方。
    b。
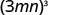
      立方体上有 3 毫米。
    使用产品属性的力量，\((ab)^m=a^m b^m\)。 3 cubed mm cubed n cubed n cubed
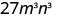
    简化。 27 厘米立方体。
    示例\(\PageIndex{23}\)

    简化：

    1. \((-12 y)^{2}\)
    2. \((2 w x)^{5}\)
    回答
    1. \(144y^{2}\)
    2. \(32w^{5} x^{5}\)
    示例\(\PageIndex{24}\)

    简化：

    1. \((5 w x)^{3}\)
    2. \((-3 y)^{3}\)
    回答
    1. 125\(w^{3} x^{3}\)
    2. \(-27 y^{3}\)

    通过应用多个属性来简化表达式

    现在，我们有三个属性用于将表达式与指数相乘。 让我们总结一下，然后举一些使用多个属性的示例。

    指数的属性

    如果\(a\)和\(b\)是实数，and\(m\)\(n\) 是整数，那么

    \[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]

    对于任何实数\(m\)和，所有指数属性均成立\(n\)。 现在，我们只使用整数指数。

    示例\(\PageIndex{25}\)

    简化：

    1. \(\left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\)
    2. \(\left(-6 x^{4} y^{5}\right)^{2}\)
    回答
    1. \(\begin{array}{ll}& \left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\\ {\text { Use the Power Property. }}& y^{18} \cdot y^{20} \\ {\text { Add the exponents. }} & y^{38} \end{array}\)
    2. \(\begin{array}{ll}& \left(-6 x^{4} y^{5}\right)^{2}\\ {\text { Use the Product to a Power Property. }} & {(-6)^{2}\left(x^{4}\right)^{2}\left(y^{5}\right)^{2}} \\ {\text { Use the Power Property. }} & {(-6)^{2}\left(x^{8}\right)\left(y^{10}\right)^{2}} \\ {\text { Simplify. }} & {36 x^{8} y^{10}}\end{array}\)
    示例\(\PageIndex{26}\)

    简化：

    1. \(\left(a^{4}\right)^{5}\left(a^{7}\right)^{4}\)
    2. \(\left(-2 c^{4} d^{2}\right)^{3}\)
    回答
    1. \(a^{48}\)
    2. \(-8 c^{12} d^{6}\)
    示例\(\PageIndex{27}\)

    简化：

    1. \(\left(-3 x^{6} y^{7}\right)^{4}\)
    2. \(\left(q^{4}\right)^{5}\left(q^{3}\right)^{3}\)
    回答
    1. 81\(x^{24} y^{28}\)
    2. \(q^{29}\)
    示例\(\PageIndex{28}\)

    简化：

    1. \((5 m)^{2}\left(3 m^{3}\right)\)
    2. \(\left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3}\)
    回答
    1. \(\begin{array}{ll}& (5 m)^{2}\left(3 m^{3}\right)\\{\text { Raise } 5 m \text { to the second power. }} & {5^{2} m^{2} \cdot 3 m^{3}} \\ {\text { Simplify. }} & {25 m^{2} \cdot 3 m^{3}} \\ {\text { Use the Commutative Property. }} & {25 \cdot 3 \cdot m^{2} \cdot m^{3}} \\ {\text { Multiply the constants and add the exponents. }} & {75 m^{5}}\end{array}\)
    2. \(\begin{array}{ll} & \left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3} \\ \text{Use the Product to a Power Property.} & \left(3^{4} x^{8} y^{4}\right)\left(2^{3} x^{3} y^{6}\right)\\\text{Simplify.} & \left(81 x^{8} y^{4}\right)\left(8 x^{3} y^{6}\right)\\ \text{Use the Commutative Property.} &81\cdot 8 \cdot x^{8} \cdot x^{3} \cdot y^{4} \cdot y^{6} \\\text{Multiply the constants and add the exponents.} & 648x^{11} y^{10}\\ \end{array}\)
    示例\(\PageIndex{29}\)

    简化：

    1. \((5 n)^{2}\left(3 n^{10}\right)\)
    2. \(\left(c^{4} d^{2}\right)^{5}\left(3 c d^{5}\right)^{4}\)
    回答
    1. 75\(n^{12}\)
    2. 81\(c^{24} d^{30}\)
    示例\(\PageIndex{30}\)

    简化：

    1. \(\left(a^{3} b^{2}\right)^{6}\left(4 a b^{3}\right)^{4}\)
    2. \((2 x)^{3}\left(5 x^{7}\right)\)
    回答
    1. 256\(a^{22} b^{24}\)
    2. 40\(x^{10}\)

    乘以单项式

    由于单项式是代数表达式，因此我们可以使用指数的属性将单项式相乘。

    示例\(\PageIndex{31}\)

    乘以：\(\left(3 x^{2}\right)\left(-4 x^{3}\right)\)

    回答

    \ (\ begin {array} {ll} &\ left (3 x^ {2}\ 右)\ 左 (-4 x^ {3}\ 右)\\\ text {使用交换属性重新排列术语。} & 3\ cdot (-4)\ cdot x^ {2}\ cdot x^ {3}\\
    \ text {Multiply。} & -12 x^ {5}\ end {array}\)

    示例\(\PageIndex{32}\)

    乘以：\(\left(5 y^{7}\right)\left(-7 y^{4}\right)\)

    回答

    \(-35 y^{11}\)

    示例\(\PageIndex{33}\)

    乘以：\(\left(-6 b^{4}\right)\left(-9 b^{5}\right)\)

    回答

    54\(b^{9}\)

    示例\(\PageIndex{34}\)

    乘以：\(\left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\)

    回答

    \(\begin{array}{ll} & \left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & \frac{5}{6} \cdot 12 \cdot x^{3} \cdot x \cdot y \cdot y^{2}\\ \text{Multiply.} &10x^{4} y^{3}\end{array}\)

    示例\(\PageIndex{35}\)

    乘以：\(\left(\frac{2}{5} a^{4} b^{3}\right)\left(15 a b^{3}\right)\)

    回答

    6\(a^{5} b^{6}\)

    示例\(\PageIndex{36}\)

    乘以：\(\left(\frac{2}{3} r^{5} s\right)\left(12 r^{6} s^{7}\right)\)

    回答

    8\(r^{11} s^{8}\)

    注意

    访问以下在线资源以获取更多指导和练习使用指数的乘法属性：

    • 指数的乘法特性

    关键概念

    • 指数表示法
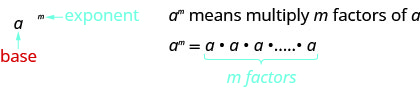
      此图有两列。 左列中是 a 到 m 的幂次方。 m 以蓝色标记为指数。 a 以红色标记为基础。 右栏是文本 “a 到 m 粉末表示乘以 a 的 m 个因子”。 在此之下是 a 到 m 的乘以 a 乘以 a，然后是省略号，下面是蓝色的 “m 因子”。
    • 指数的属性
      • 如果\(a\)和\(b\)是实数，an\(m\) d\(n\) 是整数，那么

    \[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]