5.6: 绘制线性不等式系统的图表
- Page ID
- 204349
在本节结束时,您将能够:
- 确定有序对是否为线性不等式组的解
- 通过绘图求解线性不等式系统
- 解决不等式系统的应用
确定有序对是否为线性不等式组的解
线性不等式组的定义与线性方程组的定义非常相似。
组合在一起的两个或多个线性不等式构成线性不等式系统。
线性不等式系统看起来像线性方程组,但它有不等式而不是方程。 由两个线性不等式组成的系统如下所示。
\[\left\{\begin{array}{l}{x+4 y \geq 10} \\ {3 x-2 y<12}\end{array}\right.\]
为了求解线性不等式系统,我们将找到两个不等式的解的变量的值。 我们使用每个不等式的图来求解系统,并将解显示为图表。 我们将在平面上找到包含所有使两个不等式都成真的有序对 (x, y) (x, y) 的区域。
线性不等式系统的解是使所有不等式都成真的变量的值。
线性不等式组的解显示为 x-y 坐标系中的阴影区域,该区域包括所有点的有序对使不等式成真。
为了确定有序对是否是两个不等式组的解,我们将变量的值替换为每个不等式。 如果有序对使两个不等式都成立,则这是系统的解。
确定订购的配对是否是系统的解决方案。 \(\left\{\begin{array}{l}{x+4 y \geq 10} \\ {3 x-2 y<12}\end{array}\right.\)
- (−2, 4)
- (3,1)
- 回答
-
1。 有序对(−2,4)是解决方案吗?

有序对 (−2, 4) 使两个不等式都成真。 因此 (−2, 4) 是这个系统的解决方案。
2。 订购对 (3,1) 是解决方案吗?

有序对(3,1)使一个不等式成立,但另一个不等式是错误的。 因此 (3,1) 不是该系统的解决方案。
确定订购的配对是否是系统的解决方案。 \(\left\{\begin{array}{l}{x-5 y>10} \\ {2 x+3 y>-2}\end{array}\right.\)
- (3, −1)
- (6, −3)
- 回答
-
- 不
- 是的
确定订购的配对是否是系统的解决方案。 \(\left\{\begin{array}{l}{y>4 x-2} \\ {4 x-y<20}\end{array}\right.\)
- (2,1)
- (4, −1)
- 回答
-
- 不
- 不
通过绘图求解线性不等式系统
单个线性不等式的解是边界线一侧的区域,该区域包含使不等式成真的所有点。 由两个线性不等式组成的系统的解是一个包含两个不等式解的区域。 为了找到这个区域,我们将分别绘制每个不等式的图表,然后找到两者均为真的区域。 解总是以图表形式显示。
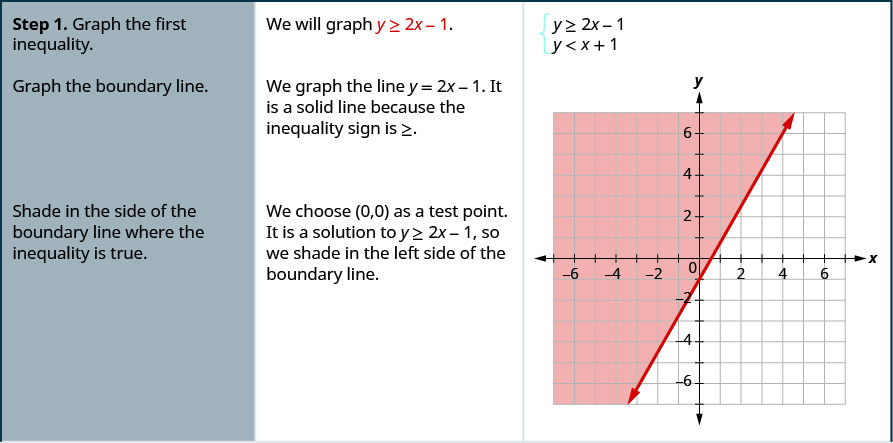
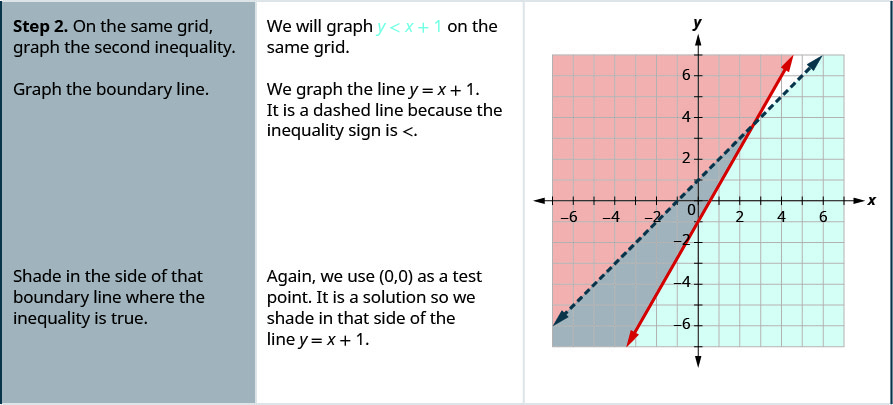
通过绘图求解系统。 \(\left\{\begin{array}{l}{y \geq 2 x-1} \\ {y<x+1}\end{array}\right.\)
- 回答
-


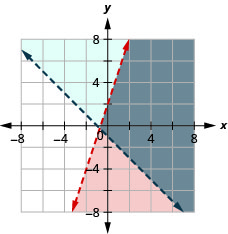
通过绘图求解系统。 \(\left\{\begin{array}{l}{y<3 x+2} \\ {y>-x-1}\end{array}\right.\)
- 回答
-
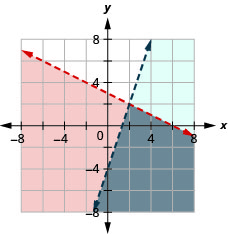
通过绘图求解系统。 \(\left\{\begin{array}{l}{y<-\frac{1}{2} x+3} \\ {y<3 x-4}\end{array}\right.\)
- 回答
-
- 绘制第一个不等式的图表。
- 绘制边界线图。
- 存在不等式的边界线一侧的阴影。
- 在同一个网格上,绘制第二个不等式。
- 绘制边界线图。
- 在不等式为真的那条边界线一侧的阴影。
- 解决方案是阴影重叠的区域。
- 通过选择测试点进行检查。
通过绘图求解系统。 \(\left\{\begin{array}{l}{x-y>3} \\ {y<-\frac{1}{5} x+4}\end{array}\right.\)
- 回答
-
通过绘制 x − y = 3 并
测试一个点来绘制图 x − y > 3。
截距为 x = 3 和 y = −3,边界
线将以虚线表示。
测试 (0, 0)。 它使不平等成为错误。 因此,将不包含 (0, 0) 的一面涂上红色
阴影。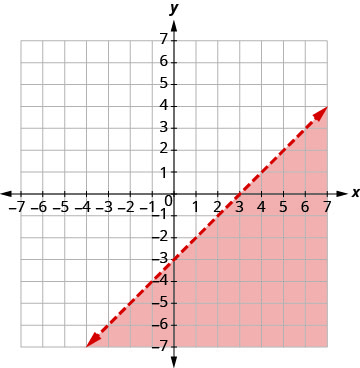
两条线的交点不包括在内,因为两条边界线都是虚线。 解决方案是两次阴影区域,即阴影较暗的区域。
使用斜率 m=−15 和 y −intercept
b = 4 绘制 y=−15x+4 来绘制 y<−15x+4 的图形。 边界线将用虚线表示。
测试 (0, 0)。 它使不等式成真,因此请将包含 (0, 0) 的一面遮住蓝色。
在解中选择一个测试点并验证它是否是两个不等式的解。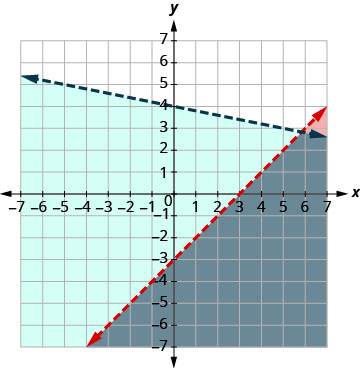
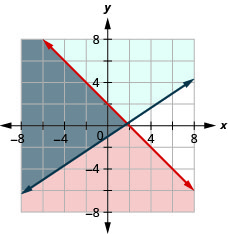
通过绘图求解系统。 \(\left\{\begin{array}{l}{x+y \leq 2} \\ {y \geq \frac{2}{3} x-1}\end{array}\right.\)
- 回答
-
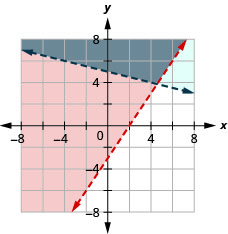
通过绘图求解系统。 \(\left\{\begin{array}{l}{3 x-2 y \leq 6} \\ {y>-\frac{1}{4} x+5}\end{array}\right.\)
- 回答
-
通过绘图求解系统。 \(\left\{\begin{array}{l}{x-2 y<5} \\ {y>-4}\end{array}\right.\)
- 回答
-
通过绘制 x−2y=5 并测试一个点来绘制 x−2y<5 图。
截距为 x = 5 和 y = −2.5,边界线将以虚线表示。
测试 (0, 0)。 它使不平等成为现实。 因此,将包含 (0, 0) 的一面
涂上红色阴影。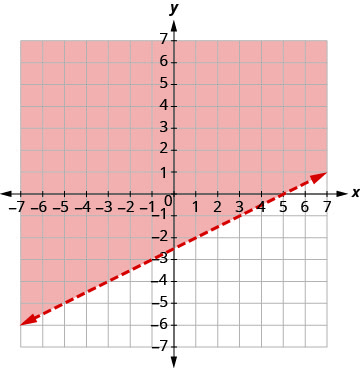
Graph y > −4,通过绘制 y = −4 并识别出它是穿过 y = −4 的
水平线。 边界线将用虚线表示。
测试 (0, 0)。 它使不平等成为现实。 因此,
将包含 (0, 0) 的一面遮光(蓝色)。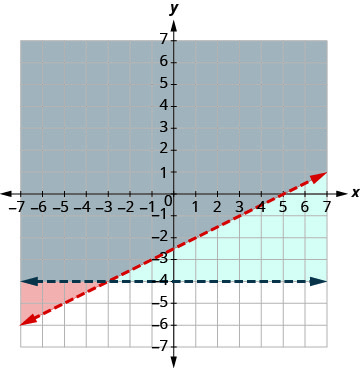
点 (0, 0) 在解中,我们已经发现它是每个不等式的解。 两条线的交点不包括在内,因为两条边界线都是虚线。
解决方案是两次阴影区域,即阴影较暗的区域。
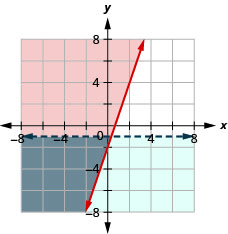
通过绘图求解系统。 \(\left\{\begin{array}{l}{y \geq 3 x-2} \\ {y<-1}\end{array}\right.\)
- 回答
-
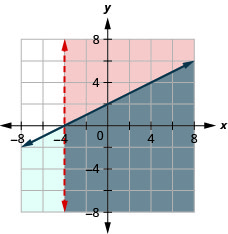
通过绘图求解系统。 \(\left\{\begin{array}{l}{x>-4} \\ {x-2 y \leq-4}\end{array}\right.\)
- 回答
-
边界线平行的线性不等式系统可能没有解。 我们将在示例中看到这一点\(\PageIndex{13}\)。
通过绘图求解系统。 \(\left\{\begin{array}{l}{4 x+3 y \geq 12} \\ {y<-\frac{4}{3} x+1}\end{array}\right.\)
- 回答
-
绘制图形\(4x+3y\geq 12\),通过绘制 4x+3y=12 并测试一个点来绘制。
截距为 x = 3 和 y = 4,边界线将为实线。
测试 (0, 0)。 它使不平等成为错误。 因此,将不包含 (0, 0) 的一面涂上红色
阴影。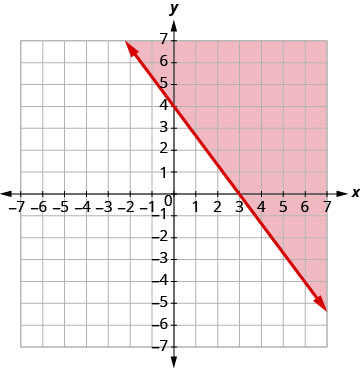
两个阴影区域都没有点,因此系统没有解。 这个系统没有解决办法。\(y=−\frac{4}{3}x+1\)使用
斜率\(m = \frac{4}{3}\)和 y 截距 b = 1 绘制图\(y<−\frac{4}{3}x+1\)形。 边界线将用虚线表示。
测试 (0, 0)。 它使不平等成为现实。 因此,将包含 (0, 0) 的一面涂上蓝色
阴影。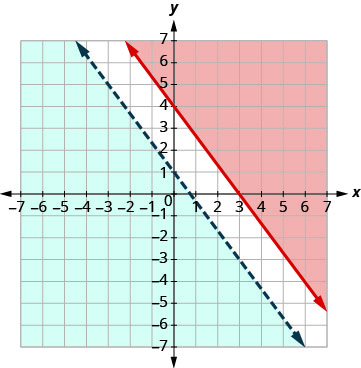
通过绘图求解系统。 \(\left\{\begin{array}{l}{3 x-2 y \leq 12} \\ {y \geq \frac{3}{2} x+1}\end{array}\right.\)
- 回答
-
没有解决办法
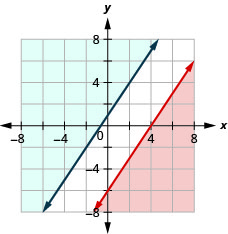
通过绘图求解系统。 \(\left\{\begin{array}{l}{x+3 y>8} \\ {y<-\frac{1}{3} x-2}\end{array}\right.\)
- 回答
-
没有解决办法
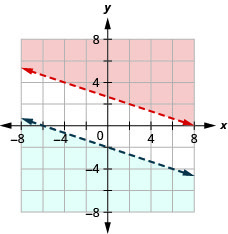
通过绘图求解系统。 \(\left\{\begin{array}{l}{y>\frac{1}{2} x-4} \\ {x-2 y<-4}\end{array}\right.\)
- 回答
-
\(y=\frac{1}{2}x−4\)
使用斜率\(m=\frac{1}{2}\)和截距
b = −4 绘制图\(y>\frac{1}{2}x−4\)形。 边界线将用虚线表示。
测试 (0, 0)。 它使不平等成为现实。 因此,将包含 (0, 0) 的一面涂上红色
阴影。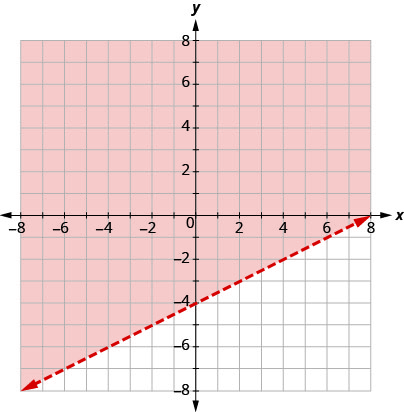
通过绘制 x−2y=−4x−2y=−4 并测试一个点来绘制 x−2y<−4 图 x−2y<−4。
截距为 x = −4 和 y = 2,边界
线将以虚线表示。
在解中选择一个测试点并
验证它是否是两个不等式的解。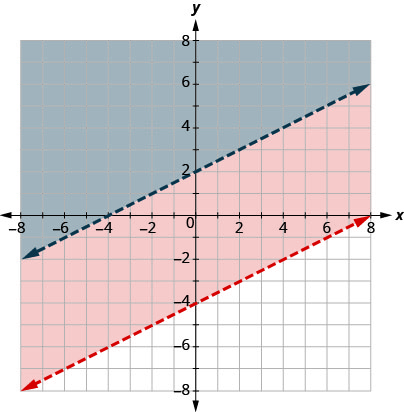
解中不包括边界线上的任何点,因为两条线都是虚线。
解是经过两次阴影的区域,这也是 x−2y<−4 的解。
通过绘图求解系统。 \(\left\{\begin{array}{l}{y \geq 3 x+1} \\ {-3 x+y \geq-4}\end{array}\right.\)
- 回答
-
\(y \geq 3 x+1\)
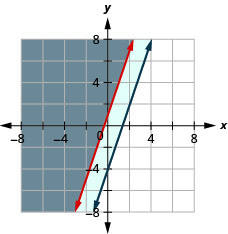
通过绘图求解系统。 \(\left\{\begin{array}{l}{y \leq-\frac{1}{4} x+2} \\ {x+4 y \leq 4}\end{array}\right.\)
- 回答
-
\(x+4 y \leq 4\)

求解不等式系统的应用
要解决不等式系统的应用,我们需要做的第一件事就是将每个条件转化为不等式。 然后我们像上面那样绘制系统图,以查看包含解的区域。 许多情况只有在两个变量均为正时才是真实的,因此它们的图表只会显示 Quadrant I。
克里斯蒂在街头集市的摊位上出售她的照片。 一开始,她希望在自己的展位上展示至少 25 张照片。 她展示的每张小照片要花4美元,每张大照片要花10美元。 她不想花超过200美元购买要展示的照片。
- 编写一个不等式系统来模拟这种情况。
- 绘制系统图表。
- 她能展示15张小照片和5张大照片吗?
- 她能展示3张大照片和22张小照片吗?
- 回答
-
1.让 x= 小照片的数量。
y= 大型照片的数量
要找到不等式系统,请翻译信息。
\(\begin{array}{c}{\text { She wants to have at least } 25 \text { photos. }} \\ {\text { The number of small plus the number of large should be at least } 25 .} \\ {x+y \geq 25} \\ {\$ 4 \text { for each small and } \$ 10 \text { for each large must be no more than } \$ 200} \\ {4 x+10 y \leq 200}\end{array}\)
我们有我们的不平等体系。 \(\left\{\begin{array}{l}{x+y \geq 25} \\ {4 x+10 y \leq 200}\end{array}\right.\)2。
要绘制图形\(x+y\geq 25\),请将 x + y = 25 绘制为实线。
选择 (0, 0) 作为测试点。 由于它不能使不等式成
真,因此请将不包括点 (0, 0) 的一侧涂成红色。
要绘制图表\(4x+10y\leq 200\),请将 4 x + 10 y = 200 绘制为实线。
选择 (0, 0) 作为测试点。 由于它不能使不等式成
真,因此请将包含点 (0, 0) 的边变为蓝色。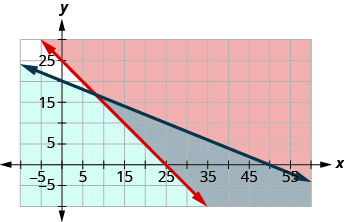
系统的解决方案是图形的区域呈双重阴影,因此阴影较暗。3。 为了确定 10 张小照片和 20 张大照片是否有效,我们看看点 (10、20) 是否在解区内。 不是。 克里斯蒂不会显示 10 张小照片和 20 张大照片。
4。 为了确定 20 张小照片和 10 张大照片是否有效,我们看看点 (20、10) 是否在解区内。 确实如此。 克里斯蒂可以选择显示 20 张小照片和 10 张大照片。
请注意,我们还可以通过将值替换为每个不等式来测试可能的解决方案。
拖车的最大重量为 160 磅,最大体积为 15 立方英尺。 微波炉重 30 磅,体积为 2 立方英尺,而打印机重 20 磅,有 3 立方英尺的空间。
- 编写一个不等式系统来模拟这种情况。
- 绘制系统图表。
- 这辆拖车能否携带 4 台微波炉和 2 台打印机?
- 这辆拖车能否携带 7 台微波炉和 3 台打印机?
- 回答
-
- \(\left\{\begin{array}{l}{30 m+20 p \leq 160} \\ {2 m+3 p \leq 15}\end{array}\right.\)
3. 是的
4. 没有
玛丽需要购买答卷和铅笔用品,以便为高中的大三学生提供标准化考试。 所需的答卷数量至少比铅笔数量多 5 张。 铅笔的价格为2美元,答卷的价格为1美元。 玛丽购买这些用品的预算允许的最高费用为400美元。
- 编写一个不等式系统来模拟这种情况。
- 绘制系统图表。
- 玛丽可以买 100 支铅笔和 100 张答卷吗?
- 玛丽可以买 150 支铅笔和 150 张答卷吗?
- 回答
-
- \(\left\{\begin{array}{l}{a \geq p+5} \\ {a+2 p \leq 400}\end{array}\right.\)
3. 没有
4. 没有
奥马尔在进行团队练习之前需要消耗至少 800 卡路里的热量。 他想要的只是汉堡包和饼干,而且他不想花超过5美元。 在他学院附近的汉堡店,每个汉堡包含有240卡路里的热量,价格为1.40美元。 每个饼干含有160卡路里的热量,价格为0.50美元。
- 编写一个不等式系统来模拟这种情况。
- 绘制系统图表。
- 他能吃 1 块饼干和 3 个汉堡包吗?
- 他能吃 4 个饼干和 2 个汉堡包吗?
- 回答
-
假设 h = 汉堡包的数量。
c= cookie 的数量
要找到不等式系统,请翻译信息。
每个汉堡包的卡路里为240卡路里,再加上饼干中每个160卡路里的热量必须超过800卡路里。\[240 h+160 c \geq 800\]
购买汉堡包的金额为每个 1.40 美元,加上购买饼干的每个 0.50 美元,必须不超过 5.00 美元。
\[1.40 h+0.50 c \leq 5\]
\(\text { We have our system of inequalities. } \quad \left\{\begin{array}{l}{240 h+160 c \geq 800} \\ {1.40 h+0.50 c \leq 5}\end{array}\right.\)
2。
将\(240h+160c\geq 800\)图形 240h+160c=800 绘制为实线。
选择 (0, 0) 作为测试点。它不会使不等式成真。
因此,对不包括点 (0, 0) 的一侧进行阴影(红色)。
如图所\(1.40 h+0.50 c \leq 5\)示,将 1.40h+0.50c=5 绘制为实线。
选择 (0,0) 作为测试点。 它使不平等成为现实。 因此,将包含该点的一面加上阴影
(蓝色)。
系统的解决方案是图形的区域呈双重阴影,因此阴影较暗。
3。 为了确定 1 个饼干和 3 个汉堡包是否符合奥马尔的标准,我们看看点 (1、3) 是否在解决方案区域。 不是。
4。 为了确定 4 个饼干和 2 个汉堡包是否符合奥马尔的标准,我们看看问题(4、2)是否在解决方案区域。 确实如此。 他可能会选择吃 4 个饼干和 2 个汉堡包。我们还可以通过将值替换为每个不等式来测试可能的解决方案。
紧张情绪每天至少需要额外消耗 1,000 卡路里的热量,为跑马拉松做准备。 他只有25美元可以花在他需要的额外食物上,并且会花在0.75美元的甜甜圈上,每个甜甜圈含有360卡路里的热量和含有110卡路里的2美元的能量饮料。
- 写一个不等式系统来模拟这种情况。
- 绘制系统图表。
- 他能买 8 个甜甜圈和 4 杯能量饮料吗?
- 他能买 1 个甜甜圈和 3 杯能量饮料吗?
- 回答
-
- \(\left\{\begin{array}{l}{0.75 d+2 e \leq 25} \\ {360 d+110 e \geq 1000}\end{array}\right.\)
3. 是的
4. 没有
菲利普的医生告诉他,他应该在日常饮食中每天至少增加1000卡路里的热量。 菲利普想购买每块价格为1.80美元、含有140卡路里的蛋白质棒,以及每瓶价格为1.25美元、含有125卡路里的果汁。 他不想花超过12美元。
- 写一个不等式系统来模拟这种情况。
- 绘制系统图表。
- 他能买 3 块蛋白棒和 5 瓶果汁吗?
- 他能买 5 块蛋白棒和 3 瓶果汁吗?
- 回答
-
- \(\left\{\begin{array}{l}{140 p+125 j \geq 1000} \\ {1.80 p+1.25 j \leq 12}\end{array}\right.\)
3. 是的
4. 没有
关键概念
- 通过绘图求解线性不等式系统
- 绘制第一个不等式的图表。
- 绘制边界线图。
- 存在不等式的边界线一侧的阴影。
- 在同一个网格上,绘制第二个不等式。
- 绘制边界线图。
- 在不等式为真的那条边界线一侧的阴影。
- 解决方案是阴影重叠的区域。
- 通过选择测试点进行检查。
- 绘制第一个不等式的图表。
词汇表
- 线性不等式系统
- 组合在一起的两个或多个线性不等式构成线性不等式系统。


