5.5:使用方程组求解混合应用
- Page ID
- 204367
在本节结束时,您将能够:
- 求解混合应用
- 解决利息申请
求解混料应用程序
当我们之前用硬币和彩票解决混合应用程序时,我们首先创建了一个表格,这样我们就可以整理信息。 举一个带有镍和硬币的硬币示例,表格如下所示:
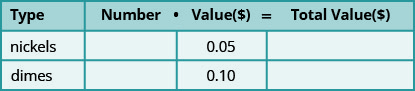
使用一个变量意味着我们必须将镍的数量和一角钱的数量联系起来。 我们必须决定是让 n 成为镍的数量,然后用 n 写出硬币的数量,还是让 d 成为一角钱并用 d 写出镍的数量。
现在我们知道如何用两个变量求解方程组,我们只让 n 是镍数,d 是角钱数。 我们将像以前一样根据总值列写一个方程,另一个方程将来自数字列。
在第一个例子中,我们将解决门票问题,门票价格以整美元为单位,因此我们暂时不需要使用小数。
转换为方程组并求解:
一家电影院的票房售出了147张晚间节目的门票,总收入为1,302美元。 售出了多少张11美元的成人票和多少8美元的儿童票?
- 回答
-
第 1 步。 阅读问题。 我们将创建一个表来组织信息。 第 2 步。 确定我们在寻找什么。 我们正在寻找成人票的数量
和售出的儿童票数量。第 3 步。 说出我们要找的东西。 假设 a= 成人票的数量。
c= 儿童票的数量表格将帮助我们整理数据。
我们有两种类型的门票:成人和儿童。写上 a 和 c 作为门票数量。 在 “号码” 列的
底部写下售出的门票总数。总共售出了 147 个。 在 “值” 列中写下每种类型票证的
值。每张成人票的价值为11美元。
每张儿童票的价值为8美元。乘以该值得出总
价值,因此成人票的总价值为
\(a\cdot 11=11a\),儿童
票的总价值为\(c\cdot 8=8c\)。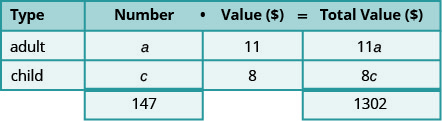
门票的总价值为
1,302美元。填写总值列。 第 4 步。 转换为方程组。 “数字” 列和 “总值
” 列为我们提供了方程组。
我们将使用消除方法来解决
这个系统。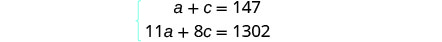
将第一个方程乘以 −8。 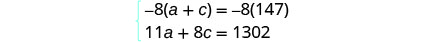
简化并添加,然后求解 a。 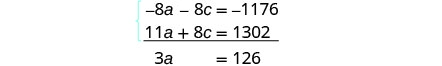

用 a = 42 代入第一个方程,
然后求解 c。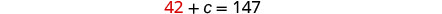
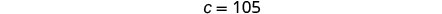
第 5 步。 检查问题中的答案。
42 张成人票,每张门票 11 美元,每张票为 462 美元
105 张儿童票,每张门票 8 美元,每张 840 美元。
总收入为1,302美元。 ✓第 6 步。 回答问题。 电影院售出了 42 张成人票和 105 张儿童票。
转换为方程组并求解:
动物园的售票处有一天售出了553张门票。 收据总额为3,936美元。 售出了多少张9美元的成人票和多少6美元的儿童票?
- 回答
-
共售出206张成人票,售出347张儿童票。
转换为方程组并求解:
一个科学中心在一个繁忙的周末售出了1,363张门票。 收据总额为12,146美元。 售出了多少张 12 美元的成人票和多少 7 美元的儿童票?
- 回答
-
共售出521张成人票,售出842张儿童票。
在练习中,\(\PageIndex{4}\)我们将解决硬币问题。 既然我们已经知道如何使用由两个变量组成的系统,那么在 “数字” 列中命名变量就很容易了。
转换为方程组并求解:
Priam拥有一系列镍和四分之一,总价值为7.30美元。 镍的数量是六个,少于季度数的三倍。 他有多少镍和多少个季度?
- 回答
-
第 1 步。 阅读问题。 我们将创建一个表来组织信息。 第 2 步。 确定我们在寻找什么。 我们正在寻找镍的数量
和季度数。第 3 步。 说出我们要找的东西。 假设 n= 镍的数量。
q = 季度数表格将帮助我们整理数据。
我们有两种类型的硬币,镍
和硬币。写上 n 和 q 作为每种硬币的编号。 在 “价值” 列中填写每
种硬币的价值。每种镍的价值为0.05美元。
每个季度的价值为0.25美元。该值的乘以得出总
值,因此,镍的总值为
n (0.05) = 0.05 n,
季度的总值为 q (0.25) = 0.25 q。
这些硬币的总价值
为7.30美元。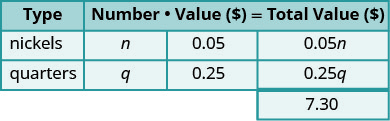
第 4 步。 转换为方程组。 总值列给出一个方程。 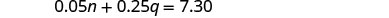
我们还知道镍的数量
比季度数少了六倍。
翻译得到第二个方程。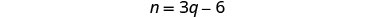
现在我们有了要解决的系统。 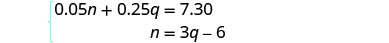
第 5 步。 求解方程组
我们将使用替换方法。
将 n = 3 q − 6 代入第一个方程。
简化并求解 q。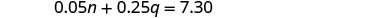
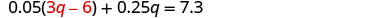
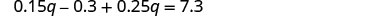
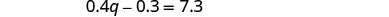
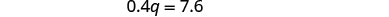
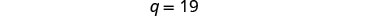
要找到镍的数量,请在第二个方程中替换
q = 19。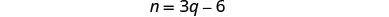
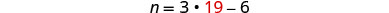
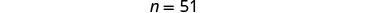
第 6 步。 检查问题中的答案。
\(\begin{aligned} 19 \text { quarters at } \$ 0.25 &=\$ 4.75 \\ 51 \text { ickels at } \$ 0.05 &=\$ 2.55 \\ \text { Total } &=\$ 7.30 \checkmark \\ 3 \cdot 19-16 &=51 \checkmark\end{aligned}\)第 7 步。 回答问题。 Priam 有 19 个四分之一和 51 个镍。
转换为方程组并求解:
玛蒂尔达有几个季度和一毛钱,总价值为8.55美元。 季度数为 3,是硬币数的两倍多。 她有多少毛钱,有多少季度?
- 回答
-
玛蒂尔达有 13 毛钱和 29 个季度。
转换为方程组并求解:
胡安有一袋镍和一角钱。 硬币的总价值为8.10美元。 硬币的数量为9,少于镍数的两倍。 胡安有多少镍和多少硬币?
- 回答
-
胡安有 36 个镍和 63 角钱。
一些混合物的应用涉及混合食物或饮料。 示例情况可能包括将葡萄干和坚果混合制成混合物,或者使用两种类型的咖啡豆制作混合物。
转换为方程组并求解:
卡森想用坚果和巧克力片制作 20 磅的混合物。 他的预算要求混合越野车每磅花费7.60美元。 坚果的价格为每磅9.00美元,巧克力片的价格为每磅2.00美元。 他应该用多少磅的坚果和多少磅的巧克力片?
- 回答
-
第 1 步。 阅读问题。 我们将创建一个表来组织信息。 第 2 步。 确定我们在寻找什么。 我们正在寻找坚果的磅数
和巧克力片的磅数。第 3 步。 说出我们要找的东西。 假设 n= 坚果的磅数。
c= 筹码的磅数Carson 会混合坚果和巧克力片
来混合。
用 n 和 c 写下坚果和巧克力片
的磅数。
会有 20 磅的越野混合物。
在 “价值” 列中输入每件商品
的每磅价格。
使用填写最后一列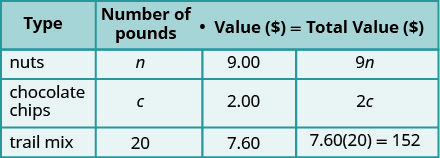
数字·价值 = 总价值 第 4 步。 转换为方程组。
我们从 “数字”
和 “总值” 列中获得方程。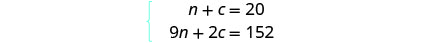
第 5 步。 求解方程组
我们将使用消除来求解方程组。将第一个方程乘以 −2 即可消除 c。 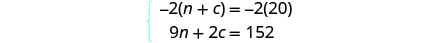
简化并添加。 求解 n。 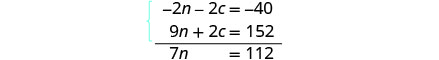
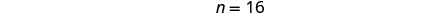
要求出
巧克力片的磅数,请在第一个方程
中替换 n = 16,然后求解 c。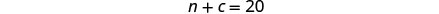
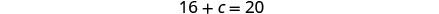
c=4 第 6 步。 检查问题中的答案。
\(\begin{aligned} 16+4 &=20 \checkmark \\ 9 \cdot 16+2 \cdot 4 &=152 \checkmark \end{aligned}\)第 7 步。 回答问题。 Carson 应该将 16 磅的坚果
和 4 磅的巧克力片混合,制成混合物。
转换为方程组并求解:
Greta 想用花生和腰果制成 5 磅的坚果混合物。 她的预算要求混合物每磅花费6美元。 花生为每磅4美元,腰果为每磅9美元。 她应该用多少磅花生和多少磅腰果?
- 回答
-
Greta 应该使用 3 磅花生和 2 磅腰果。
转换为方程组并求解:
萨米拥有制作大批辣椒所需的大部分食材。 他唯一缺少的物品是豆子和碎牛肉。 他总共需要20磅的豆类和碎牛肉,每磅的预算为3美元。 豆类的价格为每磅1美元,碎牛肉的价格为每磅5美元。 他应该买多少磅的豆子和多少磅的碎牛肉?
- 回答
-
萨米应该购买 10 磅的豆子和 10 磅的碎牛肉。
混合物问题的另一个应用涉及浓缩清洁用品、其他化学品和混合饮料。 浓度以百分比给出。 例如,浓缩20%的家用清洁剂意味着总量的20%是清洁剂,其余是水。 要制成 35 盎司的 20% 浓度,请将 7 盎司(35 盎司的 20%)的洁面乳与 28 盎司的水混合。
对于这类混合问题,我们将使用百分比而不是表中其中一列的值。
转换为方程组并求解:
萨希娜是她所在社区学院的实验室助理。 她需要用 40% 的硫酸溶液制成 200 毫升用于实验室实验。 实验室的储藏室里只有 25% 和 50% 的溶液。 她应该将 25% 和 50% 的解决方案混合多少才能制成 40% 的解决方案?
- 回答
-
第 1 步。 阅读问题。 一个数字可以帮助我们可视化情况,然后
我们将创建一个表格来组织信息。Sasheena 必须将 25% 的
溶液中的一部分和 50% 的溶液中的一部分混合
在一起,才能获得 200 毫升 40% 的溶液。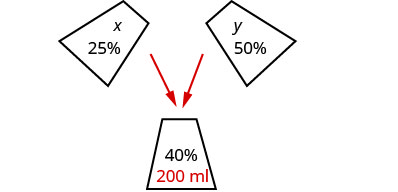
第 2 步。 确定我们在寻找什么。 我们正在寻找
她需要多少解决方案。第 3 步。 说出我们要找的东西。 假设 x= 25% 溶液的毫升数。
y= 50% 溶液的毫升数表格将帮助我们整理数据。
她将 x ml 的 25% 和 y ml 混合,获得 200 毫升 40% 的溶液。
我们在图表中将百分比写成
小数。
我们将单位数乘以浓
度得出每种溶液中的硫酸总
量。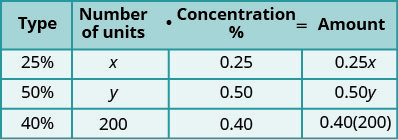
第 4 步。 转换为
方程组。 我们从
“数字” 列和 “金额
” 列中获得方程。现在我们有了系统。 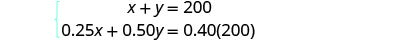
第 5 步。 求解方程组。
我们将通过淘汰来解决系统。
将第一个方程乘以 −0.5 即可
消除 y。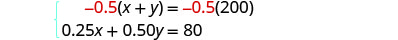
简化并添加以求解 x。 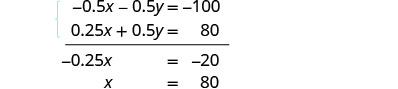
要求解 y,请在
第一个方程中替换 x = 80。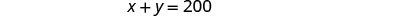
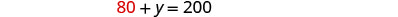
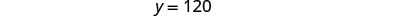
第 6 步。 检查问题中的答案。
\(\begin{array}{rll} 80+120 &=&120 \checkmark\\ 0.25(80)+0.50(120) &=&80 \checkmark \\ &&\text{Yes!} \end{array}\)第 7 步。 回答问题。 Sasheena 应将 80 毫升 25% 的溶液
与 120 毫升的 50% 溶液混合,获得 40% 溶液中的 200 毫升
。
转换为方程组并求解:
勒布朗需要150毫升的30%硫酸溶液进行实验室实验,但只能获得25%和50%的溶液。 他应该混合多少 25% 和 50% 溶液中的多少才能制成 30% 的溶液?
- 回答
-
勒布朗需要 120 毫升 25% 的溶液和 30 毫升的 50% 溶液。
转换为方程组并求解:
为了进行实验室实验,Anatole 需要用 25% 的盐酸溶液制成 250 毫升。 实验室在储藏室中只有 10% 的溶液和 40% 的溶液。 他应该混合多少 10% 和 40% 的溶液中的多少才能制成 25% 的解决方案?
- 回答
-
Anatole 应混合 125 毫升 10% 溶液和 125 毫升 40% 溶液。
解决利息申请
对利息申请进行建模的公式为 I = P rt。 利息 I 是本金 P、利率 r 和时间 t 的乘积。 在我们的工作中,我们将计算一年内获得的利息,因此 t 将为 1。
我们修改混合表中的列标题以显示兴趣公式,如您将在练习中看到的那样\(\PageIndex{13}\)。
转换为方程组并求解:
阿德南有40,000美元可供投资,并希望每年赚取7.1%的利息。 他将把一部分资金存入年利率为8%的股票基金,其余资金投入年利3%的债券。 他应该向每只基金投入多少钱?
- 回答
-
2,000股股票和7,200美元的债券。” >
您是否注意到 “本金” 栏代表投资的总金额,而 “利息” 列仅代表所得利息? 同样,我们系统中的第一个方程 s + b = 40,000 表示投资的总金额,第二个方程式 0.08 s + 0.03 b = 0.071 (40,000),代表所得利息。第 1 步。 阅读问题。 图表将帮助我们整理信息。 第 2 步。 确定我们在寻找什么。 我们正在寻找每只基金的投资金额。 第 3 步。 说出我们要找的东西。 假设s=投资于股票的金额。
b = 投资于债券的金额。将
每只基金的利率写成小数。
乘以:
本金·利率·是时候拿
到利息了。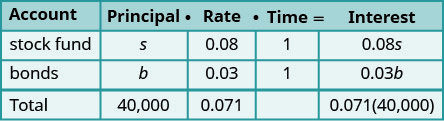
第 4 步。 转换为
方程组。
我们从 “本金” 列和 “
利息” 列中获得方程组。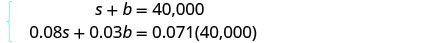
第 5 步。 求解方程组通过消除
求解。
将顶部方程乘以 −0.03。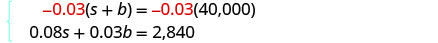
简化并添加以求解 s。 

要找出 b,请将 s = 32,800 替换到第一个方程中。 


第 6 步。 检查问题中的答案。 我们把支票留给你。 第 7 步。 回答问题。 阿德南应该投资32,800
美元的股票和7,200美元的债券。
转换为方程组并求解:
莱昂有5万美元可以投资,并希望每年赚取6.2%的利息。 他将把一部分资金存入每年收入7%的股票基金,其余的存入年收入2%的储蓄账户。 他应该向每只基金投入多少钱?
- 回答
-
莱昂应该将42,000美元存入股票基金,将8000美元存入储蓄账户。
转换为方程组并求解:
朱利叶斯向两项股票投资投资了7,000美元。 一只股票支付了11%的利息,另一只股票支付了13%的利息。 他赚取了总投资的12.5%的利息。 他在每只股票里投入了多少钱?
- 回答
-
朱利叶斯以11%的价格投资了1,750美元,以13%的价格投资了5,250美元。
转换为方程组并求解:
罗茜的两笔学生贷款欠了21,540美元。 她的银行贷款利率为10.5%,联邦贷款的利率为5.9%。 她去年支付的利息总额为1,669.68美元。 每笔贷款的本金是多少?
- 回答
-
第 1 步。 阅读问题。 图表将帮助我们整理信息。 第 2 步。 确定我们在寻找什么。 我们正在寻找每笔贷款的本金。 第 3 步。 说出我们要找的东西。 让 b = 银行贷款的本金。
f = 联邦贷款的本金贷款总额为21,540美元。 在图表
中将利率记录为小数。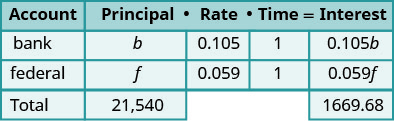
使用公式 l = Pr t 进行乘以
得利息。第 4 步。 转换为
方程组。
方程组来自 “
本金” 列和 “利息
” 列。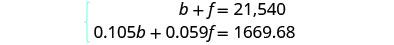
第 5 步。 求解方程组
我们将使用替换来求解。
求解 b 的第一个方程。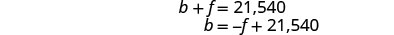
将 b = − f + 21,540 代入
第二个方程。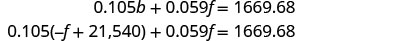
简化并求解 f。 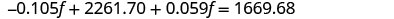
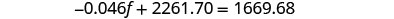
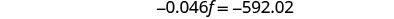
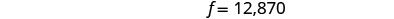
要找出 b,请将 f = 12,870 替换到第一个
方程中。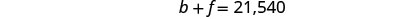
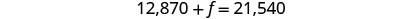
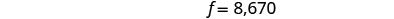
第 6 步。 检查
问题中的答案。我们把支票留给你。 第 7 步。 回答问题。 银行贷款的本金为12,870美元,
联邦贷款的本金为8,670美元。
转换为方程组并求解:
劳拉欠学生贷款18,000美元。 银行贷款的利率为2.5%,联邦贷款的利率为6.9%。 她去年支付的利息总额为1,066美元。 每笔贷款的本金是多少?
- 回答
-
银行贷款的本金为4,000美元。 联邦贷款的本金为14,000美元。
转换为方程组并求解:
Jill's Sandwich Shoppe欠两笔商业贷款65,200美元,一笔利息为4.5%,另一笔利息为7.2%。 去年所欠利息总额为3582美元。 每笔贷款的本金是多少?
- 回答
-
本金为41,200美元,占4.5%。 本金为24,000美元,占7.2%。
关键概念
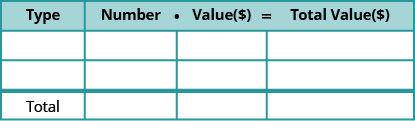
- 硬币和混合物应用表
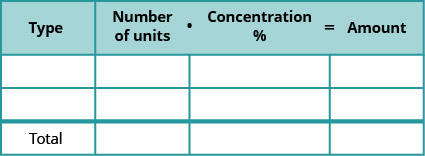
- 浓缩应用表
- 利息申请表