5.4:使用方程组求解应用程序
- Page ID
- 204407
在本节结束时,您将能够:
- 转换为方程组
- 解决直接翻译应用程序
- 求解几何应用程序
- 解决均匀运动应用程序
在本章的前面部分,我们使用线性方程组解决了几个应用程序。 在本节中,我们将介绍一些与两个数量相关的特定类型的应用程序。 我们将把单词翻译成线性方程,决定哪种是最方便使用的方法,然后求解它们。
我们将使用我们的线性方程组问题解决策略。
对线性方程组使用问题解决策略。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择变量来表示这些数量。
- 转化为方程组。
- 使用良好的代数技巧求解方程组。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
转换为方程组
我们在之前的应用程序中解决的许多问题都与两个数量有关。 以下是数学模型章节中的两个示例。
- 两个数字的总和为负十四。 一个数字比另一个数字小四个。 找到数字。
- 一对已婚夫妇每年的总收入为110,000美元。 妻子的收入少16,000美元,不到丈夫收入的两倍。 丈夫挣多少钱?
在那一章中,我们仅使用一个变量将每种情况转换为一个方程。 有时候想出如何命名这两个数量有点困难,不是吗?
让我们看看如何将这两个问题转化为具有两个变量的方程组。 我们将重点介绍问题解决策略的第 1 步到第 4 步。
转换为方程组:
两个数字的总和为负十四。 一个数字比另一个数字小四个。 找到数字。
- 回答
-




转换为方程组:
两个数字的总和为负二十三。 一个数字比另一个数字小 7。 找到数字。
- 回答
-
\(\left\{\begin{array}{l}{m+n=-23} \\ {m=n-7}\end{array}\right.\)
转换为方程组:
两个数字的总和为负十八。 一个数字比另一个数字多 40。 找到数字。
- 回答
-
\(\left\{\begin{array}{l}{m+n=-18} \\ {m=n+40}\end{array}\right.\)
我们再举一个例子,在写完方程组之后停下来。
转换为方程组:
一对已婚夫妇每年的总收入为110,000美元。 妻子的收入少16,000美元,不到丈夫收入的两倍。 丈夫挣多少钱?
- 回答
-
\(\begin{array}{ll}{\text {We are looking for the amount that }} & {\text {Let } h=\text { the amount the husband earns. }} \\ {\text {the husband and wife each earn. }} & { w=\text { the amount the wife earns }} \\ {\text{Translate.}} & {\text{A married couple together earns \$110,000.} }\\ {} & {w+h=110000} \\ & \text{The wife earns \$16,000 less than twice what} \\ & \text{husband earns.} \\ & w=2h−16,000 \\ \text{The system of equations is:} & \left\{\begin{array}{l}{w+h=110,000} \\ {w=2 h-16,000}\end{array}\right.\end{array}\)
转换为方程组:
一对夫妇的家庭总收入为84,000美元。 丈夫的收入少18,000美元,不到妻子收入的两倍。 妻子挣多少钱?
- 回答
-
\(\left\{\begin{array}{l}{w+h=84,000} \\ {h=2 w-18,000}\end{array}\right.\)
转换为方程组:
高级员工的收入低于新员工每小时收入的两倍 5美元。 他们每小时共赚43美元。 每位员工每小时的收入是多少?
- 回答
-
\(\left\{\begin{array}{l}{s=2 n-5} \\ {s+n=43}\end{array}\right.\)
解决直接翻译应用程序
我们在练习\(\PageIndex{1}\)和练习中设置了方程组,但没有求解\(\PageIndex{4}\)现在我们将情境转换为方程组,然后求解。
转换为方程组然后求解:
德文比他的儿子库珀大26岁。 他们的年龄总和为 50。 找出他们的年龄
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 我们正在寻找德文和库珀的时代。 第 3 步。 说出我们要找的东西。 让 d= 德文郡的年龄。
c= 库珀的年龄第 4 步。 转换为方程组。 德文郡比库珀大26岁。 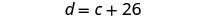
他们的年龄总和为 50。 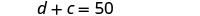
该系统是: 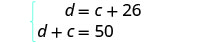
第 5 步。 求解方程组。
通过替换求解。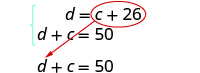
用 c + 26 代入第二个方程。 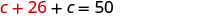
求解 c。 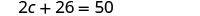
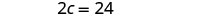
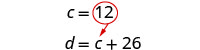
用 c = 12 代入第一个方程,然后求解 d。 
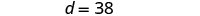
第 6 步。 检查问题中的答案。 德文郡的26岁比库珀的年龄高吗?
是的,38 比 12 多 26。
他们的年龄总和是50吗?
是的,38 加 12 等于 50。第 7 步。 回答问题。 德文是 38 岁,库珀是 12 岁。
转换为方程组然后求解:
阿里比他最小的妹妹贾米拉大12岁。 他们的年龄总和为40岁。 找出他们的年龄
- 回答
-
阿里 26 岁,贾米拉是 14 岁。
转换为方程组然后求解:
杰克的爸爸是杰克年龄的三倍多 6 倍。 他们的年龄总和为42岁。 找出他们的年龄
- 回答
-
杰克 9 岁,爸爸 33 岁。
转换为方程组然后求解:
当 Jenna 在椭圆训练器上花了 10 分钟,然后进行了 20 分钟的循环训练时,她的健身应用程序显示她消耗了 278 卡路里的热量。 当她在椭圆机训练器上花 20 分钟和 30 分钟循环训练时,她消耗了 473 卡路里的热量。 在椭圆训练机上,她每分钟消耗多少卡路里? 她每分钟循环训练消耗多少卡路里?
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 我们正在寻找
椭圆训练器每分钟
消耗的卡路里数量,以及每分钟循环训练消耗的卡
路里数量。第 3 步。 说出我们要找的东西。 假设 e= 椭圆训练机每分钟消耗的卡路里数。
c= 循环训练时每分钟消耗的卡路里数第 4 步。 转换为方程组。 在椭圆机上进行 10 分钟和循环
训练 20 分钟,消耗
278 卡路里
在椭圆机上 20 分钟和
30 分钟的循环训练消耗了
473 卡路里的热量
该系统是: 
第 5 步。 求解方程组。 将第一个方程乘以 −2 得到 e 的相反系数。 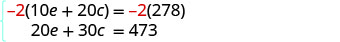
简化并添加方程。
求解 c。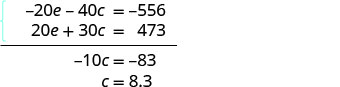
将 c = 8.3 替换为原始方程之一来求解 e。 




第 6 步。 检查问题中的答案。 自己检查数学。 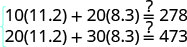
第 7 步。 回答问题。 Jenna 在使用椭圆机训练时每分钟
消耗 8.3 卡路里的热量,每
分钟消耗 11.2 卡路里的热量。
转换为方程组然后求解:
Mark 去健身房做了 40 分钟的 Bikram 热瑜伽和 10 分钟的跳千斤顶。 他消耗了 510 卡路里的热量。 下次他去健身房时,他做了 30 分钟的 Bikram 热瑜伽和 20 分钟的跳千斤顶,消耗 470 卡路里的热量。 瑜伽每分钟消耗多少卡路里? 每跳千斤顶消耗多少卡路里?
- 回答
-
Mark 每分钟瑜伽消耗 11 卡路里的热量,每分钟跳千斤顶消耗 7 卡路里的热量。
转换为方程组然后求解:
艾琳花了 30 分钟在划船机上,在健身房举重 20 分钟,消耗了 430 卡路里的热量。 下次去健身房时,她在划船机上花了50分钟,举重花了10分钟,消耗了600卡路里的热量。 她在划船机上每分钟消耗多少卡路里? 她每举重一分钟消耗多少卡路里?
- 回答
-
艾琳在划船机上每分钟消耗 11 卡路里的热量,每举重一分钟消耗 5 卡路里的热量。
求解几何应用程序
当我们学习数学模型时,我们使用三角形和矩形的属性求解了几何应用程序。 现在,我们将在列表中添加一些角度的属性。
两个互补角度的测量值相加为 90 度。 两个补充角度的测量值相加为 180 度。
如果两个角度的测量值之和为 90 度,则这两个角度是互补的。
如果两个角度的测量总和为 180 度,则两个角度是补充的。
如果两个角度是互补的,我们说一个角度是另一个角度的补充。
如果两个角度是互补的,我们说一个角度是另一个角度的补充。
转换为方程组然后求解:
两个互补角的差为 26 度。 找到角度的测量值。
- 回答
-
\(\begin{array}{ll}{\textbf {Step 1. Read}\text{ the problem. }} & {} \\ {\textbf {Step 2. Identify}\text{ what we are looking for.}} & {\text {We are looking for the measure of each angle.}} \\ \\ {\textbf{Step 3. Name}\text{ what we are looking for.}} & {\text{Let x = the measure of the first angle.} }\\ {} & \text{y = the measure of the second angle} \\ \textbf{Step 4. Translate}\text{ into a system of equations.}& \text{The angles are complementary.} \\ & \text{x+y=90} \\ & \text{The difference of the two angles is 26 degrees.} \\ & \text{x−y=26} \\ \\ \text{The system is} & {\left\{\begin{array}{l}{x+y=90} \\ {x-y=26}\end{array}\right.} \\ \textbf{Step 5. Solve}\text{ the system of equations by elimination.} \\& \left\{\begin{array}{l}{x+y=90} \\ \underline{x-y=26}\end{array}\right. \\ & \quad2x\quad=116 \\ \text{Substitute x = 58 into the first equation.}& \begin{array}{lrll} &x&=&58 \\ &x+y&=&90 \\ &58+y&=&90 \\ &y&=&32\end{array} \\ \textbf{Step 6. Check}\text{ the answer in the problem.} & \\ 58+32=90\checkmark\\ 58-32=36\checkmark \\ \\ \textbf{Step 7. Answer}\text{ the question.} & \text{The angle measures are 58 degrees and 32 degrees.}\end{array}\)
转换为方程组然后求解:
两个互补角度的差为 20 度。 找到角度的测量值。
- 回答
-
角度测量值为 55 度和 35 度。
转换为方程组然后求解:
两个互补角的差为 80 度。 找到角度的测量值。
- 回答
-
角度测量值为 5 度和 85 度。
转换为方程组然后求解:
两个角度是补充的。 较大角度的测量值比小于小角度的五倍。 找出两个角度的测量值。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 我们正在寻找每个角度的测量方法。 第 3 步。 说出我们要找的东西。 假设 x= 第一个角度的度量。
y = 第二个角度的度量第 4 步。 转换为方程组。 角度是补充性的。 
较大的角度为十二小于较小角度的五倍 
系统是:
步骤 5。 求解方程替换系统。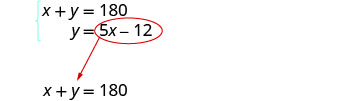
在第一个方程中用 5 x − 12 代替 y。 
求解 x。 


在第二个方程中用 32 代替,然后求解 y。 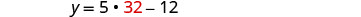


第 6 步。 检查问题中的答案。
\(\begin{aligned} 32+158 &=180 \checkmark \\ 5 \cdot 32-12 &=147 \checkmark \end{aligned}\)第 7 步。 回答问题。 角度测量值为 148 和 32。
转换为方程组然后求解:
两个角度是补充的。 较大角度的测量值是小角度的三倍多 12 度。 找到角度的测量值。
- 回答
-
角度测量值为 42 度和 138 度。
转换为方程组然后求解:
两个角度是补充的。 较大角度的测量值为 18 小于较小角度的两倍。 找到角度的测量值。
- 回答
-
角度测量值为 66 度和 114 度。
转换为方程组然后求解:
兰德尔有 125 英尺的围栏来围住他家旁边后院的矩形部分。 他只需要围绕三面围栏,因为第四面将是房屋的墙壁。 他希望围栏院子(与房屋墙壁平行)的长度是宽度的四倍多 5 英尺。 找出长度和宽度。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 我们正在寻找长度和宽度。 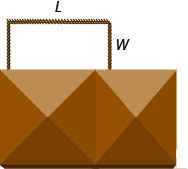
第 3 步。 说出我们要找的东西。 假设 L = 围栏码的长度。
W = 围栏院子的宽度第 4 步。 转换为方程组。 一个长度和两个宽度等于 125。 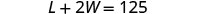
长度将比宽度的四倍多 5 英尺。 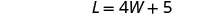
系统是:
步骤 5。 通过替换求解方程组。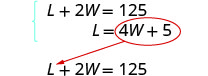
用 L = 4 W + 5 代入第一个
方程,然后求解 W。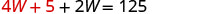
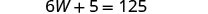
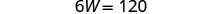
在第二个
方程中用 20 代替 W,然后求解 L。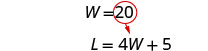
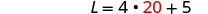
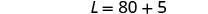
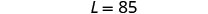
第 6 步。 检查问题中的答案。
\(\begin{array}{rll} 20+28+20&=&125\checkmark \\ 85 &=&4\cdot 20 + 5\checkmark\end{array}\)第 7 步。 回答方程式。 长度为 85 英尺,宽度为 20 英尺。
转换为方程组然后求解:
马里奥想在他后院的游泳池周围放一个矩形围栏。 由于一侧与房屋相邻,他只需要将三面围起来。 有两个长边,一个较短的一边与房子平行。 他需要 155 英尺的围栏来封闭游泳池。 长边的长度小于 10 英尺,小于宽度的两倍。 找出要封闭的泳池区域的长度和宽度。
- 回答
-
长度为 60 英尺,宽度为 35 英尺。
转换为方程组然后求解:
亚历克西斯想在邻居围栏旁边的院子里建造一只矩形的狗跑道。 她将使用 136 英尺的围栏将矩形狗跑道完全封闭。 狗沿着邻居围栏奔跑的长度将小于宽度的两倍16英尺。 找出狗跑的长度和宽度。
- 回答
-
长度为 60 英尺,宽度为 38 英尺。
求解均匀运动应用程序
前面介绍均匀运动问题时,我们使用表格来整理这些问题的信息。 我们将继续使用此表。 基本方程为 D = r t,其中 D 是行进距离,r 是速率,t 是时间。
我们的第一个均匀运动应用示例将针对类似于我们已经看到的情况,但现在我们可以使用两个变量和两个方程了。
转换为方程组然后求解:
乔尼在州际公路上离开圣路易斯,以每小时 65 英里的速度向西行驶向丹佛。 半小时后,凯利以与乔尼相同的路线离开圣路易斯,每小时行驶78英里。 凯利要多久才能赶上 Joni?
- 回答
-
图表有助于我们直观地了解情况。

识别并命名我们要找的东西。
图表将帮助我们整理数据。
我们知道 Joni 和 Kelly 的汇率,因此
我们在图表中输入了它们。我们正在寻找 Kelly、
k 和 Joni、j 各自开车的时间长度。
由于 d=r·t 我们可以填写 “距离” 列。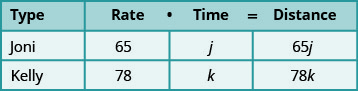
转化为方程组。
要形成方程组,我们必须认识到 Kelly 和 Joni 的行驶距离相同。 所以,65j=78k。
此外,由于凯利稍后离开,她的时间将比乔尼的时间少1212小时。
所以,k=j−12。现在我们有了系统。 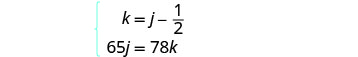
通过替换求解方程组。 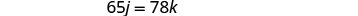
用 k=j−12 代入第二个方程,然后求解 j。 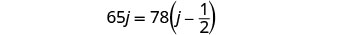
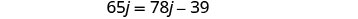
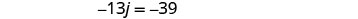

要找出 Kelly 的时间,用 j = 3 代入第一个方程,然后求解 k。 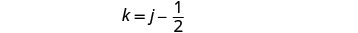
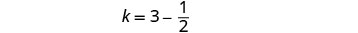
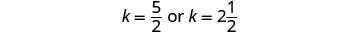
检查问题中的答案。
Joni 3 小时(65 英里/小时)= 195 英里。
凯利\(2\frac{1}{2}\)时长(78 英里/小时)= 195 英里。
是的,他们相遇
时会走同样的距离。回答问题。 凯利会在\(2\frac{1}{2}\)几个小时内赶上 Joni。
到那时,乔尼已经旅行了 3 个小时。
转换为方程组然后求解:米切尔在州际公路上离开底特律,向南行驶至奥兰多,时速为每小时 60 英里。 一小时后,克拉克以每小时 75 英里的速度离开底特律,沿着与米切尔相同的路线行驶。 克拉克要花多长时间才能抓住米切尔?
- 回答
-
克拉克要花4个小时才能抓到米切尔。
翻译成方程组然后求解:查理以平均每小时 36 英里的速度离开了母亲的房子。 他的妹妹 Sally 在 15 分钟(1/4 小时)后离开,沿着同一条路线行驶,平均时速为 42 英里。 莎莉要等多久才能赶上查理?
- 回答
-
莎莉要花\(1\frac{1}{2}\)几个小时才能赶上查理。
许多现实世界中均匀运动的应用之所以出现,是因为水流或空气流对车辆实际速度的影响。 由于风流盛行,在美国,越野飞机向西飞行所需的时间通常比向东飞行更长。
让我们来看看在河上行驶的船。 根据船的行驶方向,水流要么减慢船速,要么加速。
图\(\PageIndex{1}\)和图\(\PageIndex{2}\)显示了河流如何影响船只的实际行驶速度。 我们将船在静止水中的速度 b 和河流的速度称为 c。
在图\(\PageIndex{1}\)中,船正在向下游行驶,方向与河流的方向相同。 潮流有助于推动船只,因此船的实际速度比在静水中的速度快。 船的实际移动速度为 b + c。
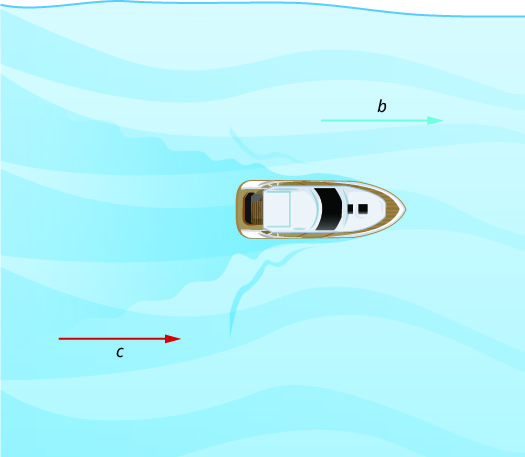
在图\(\PageIndex{2}\)中,船正在向上游行驶,与河流相反。 潮流不利于船,因此船的实际速度比它在静水中的速度慢。 船的实际速度为 b−c。
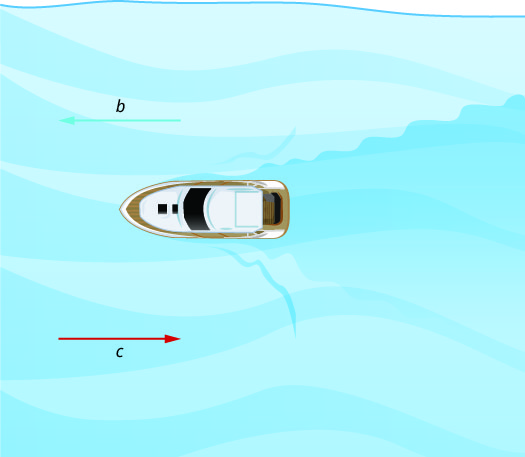
我们将在练习中为这种情况提供一些数字\(\PageIndex{25}\)。
转换为方程组然后求解:
一艘内河游轮在下游航行了 60 英里,行驶了 4 个小时,然后花了 5 个小时向上游航行才返回码头。 找出船在静水中的速度和河流的速度。
- 回答
-
阅读问题。
这是一个均匀的运动问题,一张照片可以帮助我们直观地看到情况。
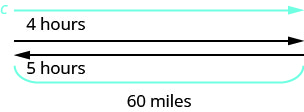
确定我们在寻找什么。 我们正在寻找飞船在静止水
中的速度和潮流的速度。说出我们要找的东西。 假设 s=s= 飞船在静止水中的速度。
c=c= 当前的速率图表将帮助我们整理信息。
这艘船先下游,然后再往上游行驶。
下游,潮流对
船舶有帮助;因此,船舶的实际费率为 s + c。
向上游移动,潮流会减慢船的速度;
因此,实际速率为 s − c。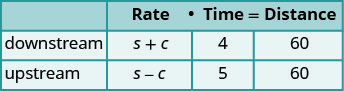
下游需要 4 个小时。
上游需要 5 个小时。
单程距离为 60 英里。转化为方程组。
由于速率时间就是距离,我们可以
编写方程组。
求解方程组。
Distribute 使两个方程都
采用标准形式,然后通过消法求解。
将顶部方程乘以 5,将底部方程乘以 4。
将方程相加,然后求解 s。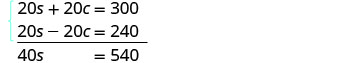
将 s = 13.5 替换为原始方程之一。 




检查问题中的答案。
下游速度将为
13.5 + 1.5 = 15 英里/小时。
在 4 小时内,船将行驶
15 · 4 = 60 英里。
上游速度将为
13.5 − 1.5 = 12 英里/小时。
在 5 个小时内,船将行驶
12 · 5 = 60 英里。回答问题。 飞船的速度为13.5英里/小时
,目前的速度为1.5英里/小时。
转换为方程组然后求解:密西西比河游船向上游航行 120 英里,行驶 12 个小时,然后花了 10 个小时才返回码头。 找出河船在静水中的速度和河流的速度。
- 回答
-
船的速度为11英里/小时,目前的速度为1英里/小时。
转换为方程组然后求解:Jason 在上游 24 英里处划独木舟 4 个小时。 他花了 3 个小时才往后划桨。 找出独木舟在静水中的速度和河流的速度。
- 回答
-
独木舟的速度为7英里/小时,当前的速度为1英里/小时。
风流影响飞机速度的方式与水流影响船速的方式相同。 我们将在练习中看到这一点\(\PageIndex{28}\)。 与飞机飞行方向相同的风流称为顺风。 向飞机方向吹来的风流称为逆风。
转换为方程组然后求解:
私人飞机可以在三个小时内顺风飞行1095英里,但在逆风后的三个小时内只能飞行987英里。 找出喷气机在静止空气中的速度和风速。
- 回答
-
阅读问题。
这是一个均匀的运动问题,一张图片可以帮助我们进行可视化。
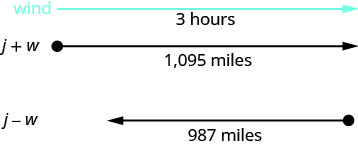
确定我们在寻找什么。 我们正在寻找喷气式飞机
在静止空气中的速度和风速。说出我们要找的东西。 让 j= 喷气机在静止空气中的速度。
w = 风速图表将帮助我们整理信息。
喷气式飞机进行了两次飞行,一次在顺风中
,一次在逆风中。
在顺风中,风有助于喷气式飞机,因此
速率为 j + w。
在逆风中,风会减慢喷气机的速度,
因此速率为 j − w。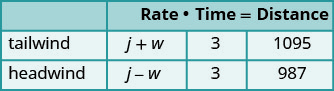
每次旅行需要 3 个小时。
飞机顺风飞行 1095 英里。
在逆风中,喷气式飞机飞行了987英里。转化为方程组。
由于速率时间就是距离,所以我们得到方
程组。
求解方程组。
分发,然后通过消除求解。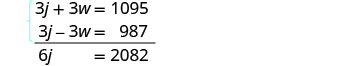
相加,然后求解 j。
将 j = 347 替换为原始方
程之一,然后求解 w。




检查问题中的答案。
顺风下,
喷气式飞机的实际速度将为
347 + 18 = 365英里/小时。
飞机将在 3 小时内行驶
365 · 3 = 1095 英里。
进入逆风时,喷气式飞机的实际
速度将为
347-18 = 329英里/小时。
飞机将在 3 小时内行驶
329 · 3 = 987 英里。回答问题。 喷气式飞机的速度为 347 英里/小时,风
速为 18 英里/小时。
转换为方程组然后求解:一架小型喷气式飞机在顺风下可以在5小时内飞行1,325英里,但在逆风的5小时内只能飞行1025英里。 找出喷气机在静止空气中的速度和风速。
- 回答
-
喷气式飞机的速度为 235 英里/小时,风速为 30 英里/小时。
转换为方程组然后求解:一架商用飞机在顺风下可以在4小时内飞行1728英里,但在逆风的4小时内只能飞行1536英里。 找出喷气机在静止空气中的速度和风速。
- 回答
-
喷气式飞机的速度为 408 英里/小时,风速为 24 英里/小时。
词汇表
- 互补角度
- 如果两个角度的测量值之和为\(90\)度,则两个角度是互补的。
- 补充角度
- 如果两个角度的测量值之和为\(180\)度,则两个角度是补充的。


