5.2:通过替换求解方程组
- Page ID
- 204312
在本节结束时,您将能够:
- 通过替换求解方程组
- 通过替换求解方程组的应用
在开始之前,请参加这个准备测验。
- 简化 −5 (3−x)。
如果你错过了这个问题,请查看练习 1.10.43。 - 简化 4−2 (n+5)。
如果您错过了此问题,请查看练习 1.10.41。 - 求解 y。8y−8=32−2y
如果你错过了这个问题,请查看练习 2.3.22。 - 求解 x. 3x−9y=−3
如果你错过了这个问题,请查看练习 2.6.22。
通过绘图求解线性方程组是可视化可能产生的解类型的好方法。 但是,在许多情况下,通过绘图求解系统不方便或不精确。 如果图形延伸到小网格之外,x 和 y 都介于 −10 和 10 之间,则绘制线条可能很麻烦。 而且,如果系统的解不是整数,则可能很难从图表中精确读出它们的值。
在本节中,我们将通过替换法求解线性方程组。
通过替换求解方程组
我们将使用最初用于绘图的相同系统。
\(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
我们将首先求解 x 或 y 的其中一个方程。 我们可以选择任一方程并求解任一变量,但我们会尽量做出让工作变得容易的选择。
然后我们将该表达式替换为另一个方程。 结果是一个只有一个变量的方程——我们知道如何求解这些变量!
找到一个变量的值后,我们会将该值替换为一个原始方程并求解另一个变量。 最后,我们检查解并确保它使两个方程都成立。
现在,我们将在 “练习” 中填写所有这些步骤\(\PageIndex{1}\)。
通过替换求解系统。 \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- 回答
-






通过替换求解系统。 \(\left\{\begin{array}{l}{-2 x+y=-11} \\ {x+3 y=9}\end{array}\right.\)
- 回答
-
(6,1)
通过替换求解系统。 \(\left\{\begin{array}{l}{x+3 y=10} \\ {4 x+y=18}\end{array}\right.\)
- 回答
-
(4,2)
- 求解任一变量的其中一个方程。
- 将步骤 1 中的表达式替换为另一个方程。
- 求解由此产生的方程。
- 将步骤 3 中的解替换为其中一个原始方程以找到另一个变量。
- 将解写成有序对。
- 检查有序对是否是两个原始方程的解。
如果系统中的一个方程是以斜率截距形式给出的,则步骤 1 已经完成了! 我们将在练习中看到这一点\(\PageIndex{4}\)。
通过替换求解系统。 \(\left\{\begin{array}{l}{x+y=-1} \\ {y=x+5}\end{array}\right.\)
- 回答
-
y 的第二个方程已经求解了。 我们将用表达式代替第一个方程中的 y。
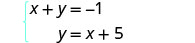
y 的第二个方程已经求解了。
我们将代入第一个方程式。将 y 替换为 x + 5。 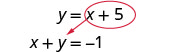
求解 x 的结果方程。 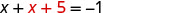
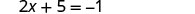
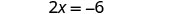
将 x = −3 替换为 y = x + 5 来找出 y。 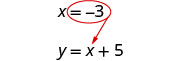
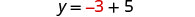
有序对是 (−3, 2)。 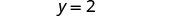
检查两个方程中的有序对:
\(\begin{array} {rllrll} x+y &=&-1 & y&=&x+5\\-3+2 &\stackrel{?}{=}&-1 &2& \stackrel{?}{=} & -3 + 5\\-1 &=&-1\checkmark &2 &=&2\checkmark \end{array}\)解是 (−3, 2)。
通过替换求解系统。 \(\left\{\begin{array}{l}{x+y=6} \\ {y=3 x-2}\end{array}\right.\)
- 回答
-
(2,4)
通过替换求解系统。 \(\left\{\begin{array}{l}{2 x-y=1} \\ {y=-3 x-6}\end{array}\right.\)
- 回答
-
(−1、−3)
如果方程是以标准形式给出的,我们需要从求解其中一个变量开始。 在下一个示例中,我们将求解 y 的第一个方程。
通过替换求解系统。 \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x+4 y=-10}\end{array}\right.\)
- 回答
-
我们需要为一个变量求解一个方程。 然后我们将该表达式替换为另一个方程。
求解 y。
代入另一个方程式。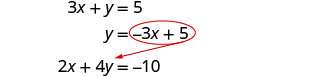
将 y 替换为 −3 x + 5。 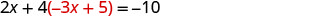
求解 x 的结果方程。 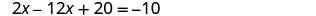
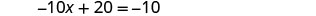
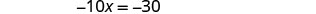
将 x = 3 替换为 3 x + y = 5 即可找到 y。 


有序对是 (3, −4)。 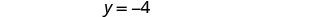
检查两个方程中的有序对:
\(\begin{array} {rllrll} 3x+y &=&5 & 2x+4y&=&-10\\3\cdot3+(-4) &\stackrel{?}{=}&5 &2\cdot3 + 4(-4)& \stackrel{?}{=} & -10\\9-4&\stackrel{?}{=}&5 &6-16& \stackrel{?}{=} & -10\\5 &=&5\checkmark &-10&=&-10\checkmark \end{array}\)解是 (3, −4)。
通过替换求解系统。 \(\left\{\begin{array}{l}{4 x+y=2} \\ {3 x+2 y=-1}\end{array}\right.\)
- 回答
-
(1, −2)
通过替换求解系统。 \(\left\{\begin{array}{l}{-x+y=4} \\ {4 x-y=2}\end{array}\right.\)
- 回答
-
(2,6)
在练习中\(\PageIndex{7}\),在第一个方程中求解 y 最容易,因为它的系数为 1。 在练习中\(\PageIndex{10}\),求解 x 会更容易。
通过替换求解系统。 \(\left\{\begin{array}{l}{x-2 y=-2} \\ {3 x+2 y=34}\end{array}\right.\)
- 回答
-
我们将求解 xx 的第一个方程,然后将该表达式替换为第二个方程。

求解 x。
代入另一个方程式。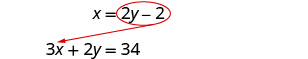
将 x 替换为 2 y − 2。 
求解 y 的结果方程。 
将 y = 5 替换为 x − 2 y = −2 即可找到 x。

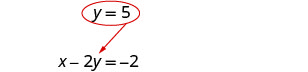



订购的货币对是 (8, 5)。 检查两个方程中的有序对:
\(\begin{array} {rllrll} x-2y &=&-2 & 3x+2y&=&34\\8-2\cdot 5 &\stackrel{?}{=}&-2 &3\cdot8 + 2\cdot5& \stackrel{?}{=} & 34\\8-10&\stackrel{?}{=}&-2 &24+10& \stackrel{?}{=} & 34\\-2 &=&-2\checkmark &34&=&34\checkmark \end{array}\)解决方案是 (8, 5)。
通过替换求解系统。 \(\left\{\begin{array}{l}{x-5 y=13} \\ {4 x-3 y=1}\end{array}\right.\)
- 回答
-
(−2、−3)
通过替换求解系统。 \(\left\{\begin{array}{l}{x-6 y=-6} \\ {2 x-4 y=4}\end{array}\right.\)
- 回答
-
(6,2)
当两个方程都已经求解了同一个变量时,很容易替换!
通过替换求解系统。 \(\left\{\begin{array}{l}{y=-2 x+5} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- 回答
-
由于两个方程都求解了 y,我们可以将一个方程替换为另一个方程。
在第一个方程中替换\(\frac{1}{2}x\) y。 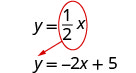
将 y 替换为\(\frac{1}{2}x\) 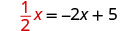
求解由此产生的方程。
首先清除分数。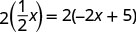
求解 x。 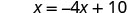
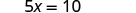
将 x = 2 替\(y = \frac{1}{2}x\)换为 y。 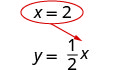
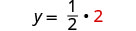
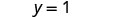
有序的货币对是 (2,1)。 检查两个方程中的有序对:
\(\begin{array} {rllrll} y &=&\frac{1}{2}x & y&=&-2x+5\\1 &\stackrel{?}{=}&\frac{1}{2}\cdot2 &1& \stackrel{?}{=} & -2\cdot2+5\\1 &=&1\checkmark &1 &=&-4+5\\ &&&1&=&1\checkmark \end{array}\)解决方案是 (2,1)。
通过替换求解系统。 \(\left\{\begin{array}{l}{y=3 x-16} \\ {y=\frac{1}{3} x}\end{array}\right.\)
- 回答
-
(6,2)
通过替换求解系统。 \(\left\{\begin{array}{l}{y=-x+10} \\ {y=\frac{1}{4} x}\end{array}\right.\)
- 回答
-
(8,2)
请务必小心下一个示例中的标志。
通过替换求解系统。 \(\left\{\begin{array}{l}{4 x+2 y=4} \\ {6 x-y=8}\end{array}\right.\)
- 回答
-
我们需要为一个变量求解一个方程。 我们将求解 y 的第一个方程。

求解 y 的第一个方程。 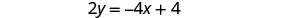
在第二个方程中用 −2 x + 2 代替 y。 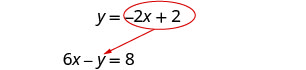
将 y 替换为 −2 x + 2。 
求解 x 的方程。 


替换\(x = \frac{5}{4}\)成 4 x + 2 y = 4 来找到 y。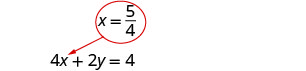



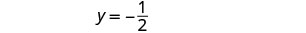
订购的对是\((\frac{5}{4},−\frac{1}{2})\)。 检查两个方程中的有序对。
\(\begin{array} {rllrll} 4x+2y &=&4& 6x-y&=&8\\4(\frac{5}{4}) +2(-\frac{1}{2})&\stackrel{?}{=}&4 &6(\frac{5}{4}) - (-\frac{1}{2})& \stackrel{?}{=} & 8\\5-1&\stackrel{?}{=}&4 &\frac{15}{4} - (-\frac{1}{2}) &\stackrel{?}{=} & 8\\4 &=&4\checkmark &\frac{16}{2} &\stackrel{?}{=}&8\\ &&&8&=&8\checkmark \end{array}\)解是 (54, −12)。
通过替换求解系统。 \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)
- 回答
-
\((2,\frac{3}{2})\)
通过替换求解系统。 \(\left\{\begin{array}{l}{4 x-y=0} \\ {2 x-3 y=5}\end{array}\right.\)
- 回答
-
\((−\frac{1}{2},−2)\)
在示例中,求解 x 或 y 的一个方程需要多做一些工作。
通过替换求解系统。 \(\left\{\begin{array}{l}{4 x-3 y=6} \\ {15 y-20 x=-30}\end{array}\right.\)
- 回答
-
我们需要为一个变量求解一个方程。 我们将求解 x 的第一个方程。
由于 0 = 0 的陈述是正确的,因此系统是一致的。 方程是相关的。 这两个方程的图形会给出相同的直线。 该系统有无限多的解决方案。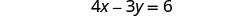
求解 x 的第一个方程。 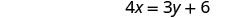
\(\frac{3}{4} y+\frac{3}{2}\)用第二个方程中的 x 代替。 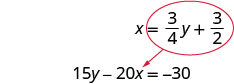
将 x 替换为\(\frac{3}{4} y+\frac{3}{2}\) 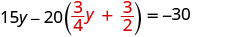
求解 y。 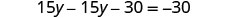
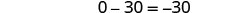

通过替换求解系统。 \(\left\{\begin{array}{l}{2 x-3 y=12} \\ {-12 y+8 x=48}\end{array}\right.\)
- 回答
-
无限多的解决方案
通过替换求解系统。 \(\left\{\begin{array}{l}{5 x+2 y=12} \\ {-4 y-10 x=-24}\end{array}\right.\)
- 回答
-
无限多的解决方案
回头看看练习中的方程式\(\PageIndex{22}\)。 有什么办法可以识别出它们是同一条线吗?
让我们看看下一个例子中会发生什么。
通过替换求解系统。 \(\left\{\begin{array}{l}{5 x-2 y=-10} \\ {y=\frac{5}{2} x}\end{array}\right.\)
- 回答
-
第二个方程已经求解了 y,因此我们可以在第一个方程中替换 y。
由于 0 = −10 是错误的陈述,因此方程不一致。 这两个方程的图形将是平行线。 该系统没有解决方案。在第一个方程中用 x 代替 y。 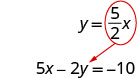
将 y 替换为\(\frac{5}{2}x\)。 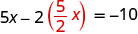
求解 x。 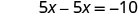

通过替换求解系统。 \(\left\{\begin{array}{l}{3 x+2 y=9} \\ {y=-\frac{3}{2} x+1}\end{array}\right.\)
- 回答
-
没有解决办法
通过替换求解系统。 \(\left\{\begin{array}{l}{5 x-3 y=2} \\ {y=\frac{5}{3} x-4}\end{array}\right.\)
- 回答
-
没有解决办法
通过替换求解方程组的应用
我们将在这里复制我们在通过图形求解方程组部分中用于求解方程组的问题解决策略。 现在我们知道如何通过替换来求解系统,这就是我们在步骤 5 中要做的。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择变量来表示这些数量。
- 转化为方程组。
- 使用良好的代数技术求解方程组。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
有些人发现用两个变量设置单词问题比只用一个变量设置它们要容易。 当你只需要写下两个字母时,选择变量名会更容易。 在下一个例子中考虑一下这个问题——你怎么能只用一个变量来做到这一点?
两个数字的总和为零。 一个数字比另一个数字少九个。 找到数字。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 我们正在寻找两个数字。 第 3 步。 说出我们要找的东西。 假设 n= 第一个数字
让 m = 第二个数字第 4 步。 转换为方程组。 两个数字的总和为零。 
一个数字比另一个数字少九个。 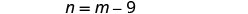
系统是: 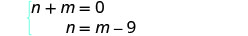
第 5 步。 求解
方程组。 我们将使用替换,
因为第二个方程为 n
求解。在第一个方程中用 m − 9 代替 n。 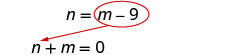
求解 m。 


代\(m=\frac{9}{2}\)入第二个方程,
然后求解 n。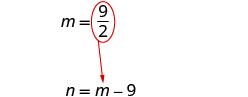
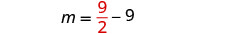
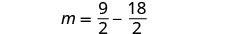
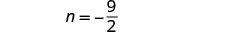
第 6 步。 检查问题中的答案。 这些数字在问题中有
意义吗? 我们会把这个留给你!第 7 步。 回答问题。 数字是\(\frac{9}{2}\)和\(-\frac{9}{2}\)。
两个数字的总和为 10。 一个数字比另一个数字少 4。 找到数字。
- 回答
-
数字是 3 和 7。
两个数字的总和为 −6。 一个数字比另一个数字少 10。 找到数字。
- 回答
-
数字是 2 和 −8。
在练习中\(\PageIndex{28}\),我们将使用矩形周长的公式,P = 2 L + 2 W。
在此处添加练习文本。
- 回答
-
第 1 步。 阅读问题。 
第 2 步。 确定你在找什么。 我们正在寻找长度和宽度。 第 3 步。 说出我们要找的东西。 假设 L = 长度
W = 宽度第 4 步。 转换为方程组。 矩形的周长为 88。 2 L + 2 W = P
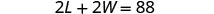
长度是五倍是宽度的两倍。 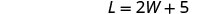
系统是: 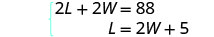
第 5 步。 求解方程组。
我们将使用替换,因为第二个
方程为 L 求解。
在第一个方程中用 2 W + 5 代替 L。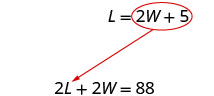
求解 W。 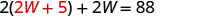
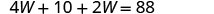
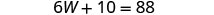
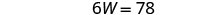
将 W = 13 替换到第二个
方程中,然后求解 L。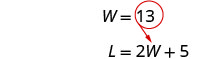
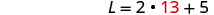
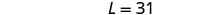
第 6 步。 检查问题中的答案。 长度为 31、宽度为
13 的矩形的周长是否为 88? 是的。第 7 步。 回答方程式。 长度为 31,宽度为 13。
矩形的周长为 40。 长度比宽度多 4。 找出矩形的长度和宽度。
- 回答
-
长度为 12,宽度为 8。
矩形的周长为 58。 长度是宽度的三倍多 5。 找出矩形的长度和宽度。
- 回答
-
长度为 23,宽度为 6。
在练习中,\(\PageIndex{31}\)我们需要记住,三角形角度的测量总和为 180 度,直角三角形有一个 90 度的角。
直角三角形中一个小角度的测量值是另一个小角度的三倍以上的十倍。 找到两个角度的测量值。
- 回答
-
我们将画一个人物并贴上标签。
第 1 步。 阅读问题。 
第 2 步。 确定你在找什么。 我们正在寻找角度的测量方法。 第 3 步。 说出我们要找的东西。 假设 a= 第 1 个角度的测量
b= 第 2 个角度的测量第 4 步。 转换为方程组。 直角三角形中一个小角
度的测量值是另一个小角度的三
倍以上的十倍。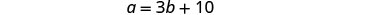
三角形角度的测量总和
为 180。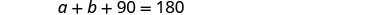
系统是: 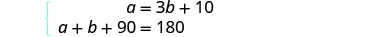
第 5 步。 求解方程组。
我们将使用替换,因为第一个
方程已求解 a。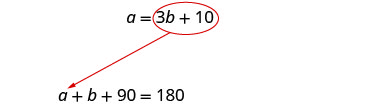
在
第二个方程中用 3 b + 10 代替 a。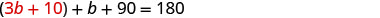
求解 b。 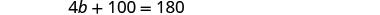


将 b = 20 替换到第一个
方程中,然后求解 a。

第 6 步。 检查问题中的答案。 我们会把这个留给你! 第 7 步。 回答问题。 小角度的测量值为
20 和 70。
直角三角形中一个小角度的测量值是另一个小角度的测量值的 2 倍多 3 倍。 找到两个角度的测量值。
- 回答
-
角度的测量值为 22 度和 68 度。
直角三角形中一个小角度的测量值小于 18,小于另一个小角度的两倍。 找到两个角度的测量值。
- 回答
-
角度的测量值为 36 度和 54 度。
希瑟在健身房当教练的薪水有两种选择。 选项 A 将向她支付 25,000 美元,另加每次训练的 15 美元。 选项 B 将为每次培训课程向她支付 10,000 美元+ 40 美元。 多少次培训会使薪资选择相等?
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 我们正在寻找
能够使薪酬相等的培训课程数量。第 3 步。 说出我们要找的东西。 让 s= Heather 的薪水。
n= 训练课程的次数第 4 步。 转换为方程组。 选项 A 将向她支付 25,000 美元
,另加每次训练的 15 美元。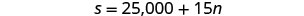
选项 B 将
为每次训练向她支付 10,000 美元+ 40 美元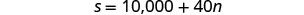
系统是: 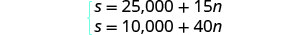
第 5 步。 求解方程组。
我们将使用替代。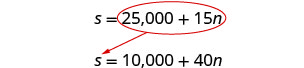
在第二个方程中用 25,000 + 15 n 代替 s。 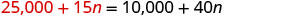
求解 n。 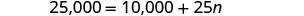
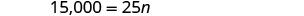

第 6 步。 检查答案。 每年 600 次培训课程是否合理?
当 n = 600 时,这两个选项是否相等?第 7 步。 回答问题。 600次培训课程的薪金选项将相等。
两家保险公司向杰拉尔丁提供了职位。 第一家公司为每售出一张保单支付12,000美元的薪水外加100美元的佣金。 第二个支付20,000美元的工资,每售出一张保单加50美元的佣金。 需要出售多少保单才能使总工资保持不变?
- 回答
-
需要出售160张保单才能使总工资保持不变。
Kenneth目前以22,000美元的薪水为A公司出售西装,每售出一套西装可获得10美元的佣金。 B公司为他提供薪水为28,000美元的职位,每售出一套西装可获得4美元的佣金。 Kenneth 需要卖出多少套西装才能使期权相等?
- 回答
-
肯尼斯需要出售 1,000 套西装。
关键概念
- 通过替换求解方程组
- 求解任一变量的其中一个方程。
- 将步骤 1 中的表达式替换为另一个方程。
- 求解由此产生的方程。
- 将步骤 3 中的解替换为其中一个原始方程以找到另一个变量。
- 将解写成有序对。
- 检查有序对是否是两个原始方程的解。


