4.1: 使用矩形坐标系

Last updated
Save as PDF

Page ID: 204713

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

在矩形坐标系中绘制点
验证两个变量中方程的解
完成线性方程的解表
在两个变量中找到线性方程的解

注意

在开始之前，请参加这个准备测验。

评估$x+3$时间$x=−1$。
如果您错过了此问题，请查看练习 1.5.25。
计算$2x−5y$何时$x=3$和 y=−2。
如果您错过了此问题，请查看练习 1.5.28。
求解 y：$40−4y=20$
如果你错过了这个问题，请查看练习 2.3.1。

在矩形坐标系上绘制点

就像地图使用网格系统来识别位置一样，代数中使用网格系统来显示矩形坐标系中两个变量之间的关系。矩形坐标系也称为 xy 平面或 “坐标平面”。

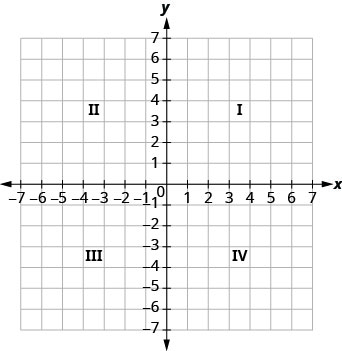
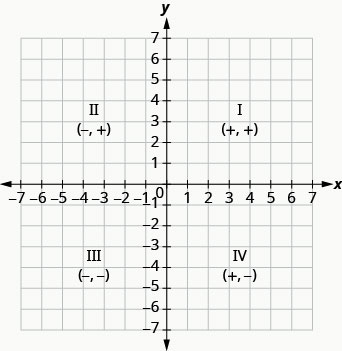
水平数字线称为 x 轴。垂直数字线称为 y 轴。 x 轴和 y 轴共同构成矩形坐标系。这些轴将一个平面分成四个区域，称为象限。象限由罗马数字标识，从右上角开始，逆时针移动。参见图$\PageIndex{1}$。

该图显示了 x y 坐标平面。 x 轴和 y 轴各从负 7 到 7 不等。飞机的右上部分标记为 “I”，飞机的左上角标记为 “II”，飞机的左下部分标记为 “III”，飞机的右下部分标记为 “IV”。 — 图$\PageIndex{1}$：“Quadrant” 的根为 “quad”，意思是 “四”。

在矩形坐标系中，每个点都由一对有序表示。有序对中的第一个数字是该点的 x 坐标，第二个数字是该点的 y 坐标。

已订购对

有序对 (x, y) (x, y) 给出矩形坐标系中点的坐标。

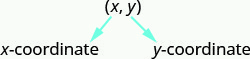
有序对 x y 被标记为第一个坐标 x 标记为 “x 坐标”，第二个坐标 y 标记为 “y 坐标”。 — 图$\PageIndex{2}$

第一个数字是 x 坐标。

第二个数字是 y 坐标。

短语 “有序配对” 表示顺序很重要。坐标轴交叉点的有序对是多少？此时两个坐标均为零，因此其有序对为$(0,0)$。这个点$(0,0)$有一个特殊的名字。它被称为起源。

起源

该点$(0,0)$被称为原点。它是 x 轴和 y 轴相交的点。

我们使用坐标在 xy 平面上定位一个点。让我们把这个点画$(1,3)$成一个例子。首先，在 x 轴上找到 1，然后轻描绘一条穿过 x=1x=1 的垂直线。然后，在 y 轴上找到 3 并绘制一条穿过 y=3y=3 的水平线。现在，找到这两条线的交汇点——即有坐标的点$(1,3)$。

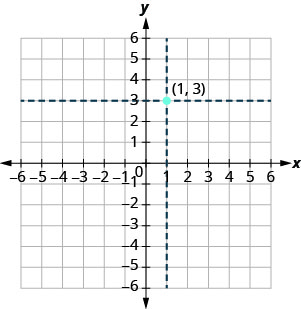
该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。箭头从原点开始，向右延伸到 x 轴上的数字 2。点 (1, 3) 已绘制并标记。两条虚线，一条平行于 x 轴，另一条平行于 y 轴，在 1、3 处垂直相交。平行于 x 轴的虚线在 3 处与 y 轴截距。平行于 y 轴的虚线在 1 处截住 x 轴。 — 图$\PageIndex{3}$

请注意，垂直线穿过$x=1$和水平线$y=3$不在图表中。我们只是用它们来帮助我们找到重点$(1,3)$。

练习$\PageIndex{1}$

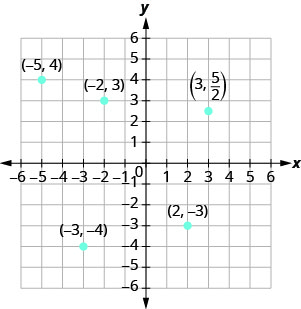
在矩形坐标系中绘制每个点并确定该点所在的象限：

(−5,4)
(−3、−4)
(2, −3)
(−2,3)
$(3, \frac{5}{2})$

回答

坐标对的第一个数字是 x 坐标，第二个数字是 y 坐标。

由于 x=−5，该点位于 y 轴的左边。此外，由于 y=4，该点位于 x 轴上方。点 (−5,4) 位于象限 II 中。
由于 x=−3，该点位于 y 轴的左边。此外，由于 y=−4，该点位于 x 轴以下。点 (−3, −4) 位于象限 III 中。
由于 x=2，该点位于 y 轴的右边。由于 y=−3，该点位于 x 轴以下。点 (2, −3) 在 Quadrant lV 中。
由于 x=−2，该点位于 y 轴的左边。由于 y=3，该点位于 x 轴上方。点 (−2,3) 在象限 II 中。
由于 x=3，该点位于 y 轴的右边。因为$y = \frac{5}{2}$，该点在 x 轴上方。（写$\frac{5}{2}$成混合数字或十进制可能会有所帮助。）重点在$(3, \frac{5}{2})$象限 I 中

该图显示了 x y 坐标平面。 x 轴和 y 轴各从负 7 到 7 不等。对点（负 5、4）、（负 2、3）、（负 3、负 4）、（3、负五半）和（2，负 3）进行绘制和标记。 — 图$\PageIndex{4}$

练习$\PageIndex{2}$

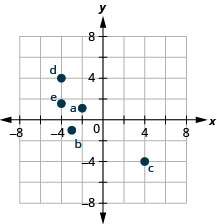
在矩形坐标系中绘制每个点并确定该点所在的象限：

(−2,1)
(−3、−1)
(4, −4)
(−4,4)
$(-4, \frac{3}{2})$

回答: $该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。点（负 2，1）被绘制并标记为 “a”。点（负 3，负 1）被绘制并标记为 “b”。点（4，负 4）被绘制并标记为 “c”。点（负 4，负一半）被绘制并标记为 “d”。$

练习$\PageIndex{3}$

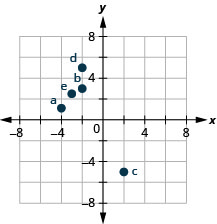
在矩形坐标系中绘制每个点并确定该点所在的象限：

(−4,1)
(−2,3)
(2, −5)
(−2,5)
$(-3, \frac{5}{2})$

回答: $该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。点（负 4，1）被绘制并标记为 “a”。点（负 2，3）被绘制并标记为 “b”。点（2，负 5）被绘制并标记为 “c”。点（负 3、2 和一半）被绘制并标记为 “d”。$

这些标志如何影响点的位置？在上一个示例中绘制点图时，您可能已经注意到了一些模式。

对于 Quadrant IV$\PageIndex{4}$ 中的图，你注意到坐标符号了什么？那么第三象限中各点的坐标符号呢？第二个象限？第一个象限？

只要看一下坐标就可以分辨出点 (−2,5) 位于哪个象限中吗？ (2, −5) 位于哪个象限？

象限

我们可以用这种方式总结象限的符号模式。

\[\begin{array}{ccc}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\]

该图显示了 x y 坐标平面。 x 轴和 y 轴各从负 7 到 7 不等。该图显示了 x y 坐标平面。 x 和 y 轴分别从 -7 到 7 延伸。飞机的右上部分标有 “I” 和 “有序对 +、+”，飞机的左上角标记为 “II” 和 “有序对-，+”，飞机的左下部分标记为 “III” “有序对-，”，飞机的右下部分标有 “IV” 和 “有序对 +，-”。 — 图$\PageIndex{5}$

如果一个坐标为零会怎样，如图所示$\PageIndex{6}$？点 (0,4) 在哪里？点 (−2,0) 在哪里？

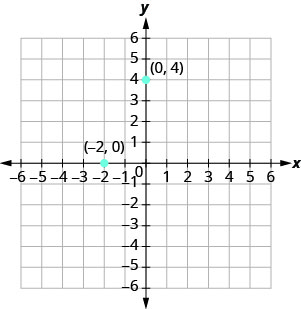
该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。绘制和标记点 (0、4) 和（负 2、0）。 — 图$\PageIndex{6}$

点 (0,4) 在 y 轴上，点 (−2,0) 在 x 轴上。

坐标轴上的点

y 坐标等于 0 的点位于 x 轴上，并具有坐标 (a,0)。

x 坐标等于 0 的点位于 y 轴上，并具有坐标 (0, b)。

练习$\PageIndex{4}$

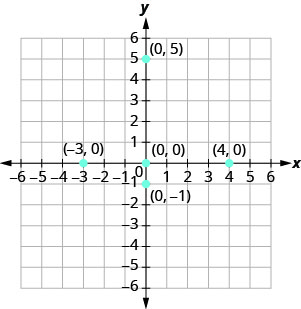
绘制每个点：

(0,5)
(4,0)
(−3,0)
(0,0)
(0, −1)

回答

由于 x=0，坐标为 (0,5) 的点位于 y 轴上。
由于 y=0，坐标为 (4,0) 的点位于 x 轴上。
由于 y=0，坐标为 (−3,0) 的点位于 x 轴上。
由于 x=0 和 y=0，坐标为 (0,0) 的点是原点。
由于 x=0，坐标为 (0, −1) 的点位于 y 轴上。

$该图显示了 x y 坐标平面。 x 轴和 y 轴各从负 7 到 7 不等。点（负 3, 0）、（0、0）、（0、负 1）、（0、负 1）、（0、5）和（4、0）均已绘制和标记。$

图$\PageIndex{7}$

练习$\PageIndex{5}$

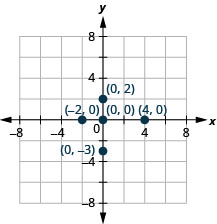
绘制每个点：

(4,0)
(−2,0)
(0,0)
(0,2)
(0, −3)。

回答: $该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。点 (4, 0)、(负 2, 0)、(0, 0)、(0、2) 和 (0, 负 3) 均已绘制和标记。$

练习$\PageIndex{6}$

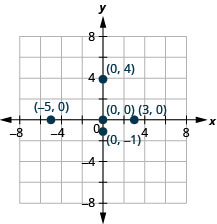
绘制每个点：

(−5,0)
(3,0)
(0,0)
(0, −1)
(0,4)。

回答: $该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。对点（负 5、0）、（3、0）、（0、0）、（0、负 1）和（0、4）进行绘制和标记。$

在代数中，能够识别图表上显示的点的坐标与能够绘制点同样重要。要识别图表上某点的 x 坐标，请读取该点正上方或下方的 x 轴上的数字。要识别一个点的 y 坐标，请直接读取该点左侧或右侧的 y 轴上的数字。请记住，当你写有序对时，请使用正确的顺序（x，y）。

练习$\PageIndex{7}$

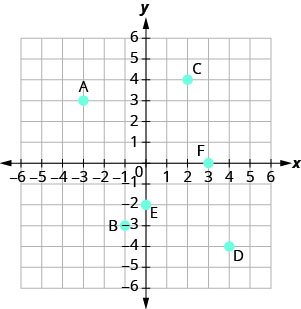
命名矩形坐标系中显示的每个点的有序对。

该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。点 (4、0)、（负 2、0）、（0、0）、（0、2）和（0，负 3）分别绘制并标记为 A、B、C、D 和 E。 — 图$\PageIndex{8}$

回答

点 A 在 x 轴上高于 −3，因此该点的 x 坐标为 −3。

该点在 y 轴上 3 的左边，因此该点的 y 坐标为 3。

该点的坐标为 (−3,3)。

点 B 在 x 轴上低于 −1，因此该点的 x 坐标为 −1。

该点位于 y 轴上 −3 的左边，因此该点的 y 坐标为 −3。

该点的坐标为 (−1, −3)。

点 C 在 x 轴上高于 2，因此该点的 x 坐标为 2。

该点在 y 轴上 4 的右侧，因此该点的 y 坐标为 4。

该点的坐标为 (2,4)。

点 D 在 x 轴上低于 4，因此该点的 x 坐标为 4。

该点位于 y 轴上 −4 的右侧，因此该点的 y 坐标为 −4。

该点的坐标为 (4, −4)。

点 E 位于 y 轴上 y=−2 处。点 E 的坐标为 (0, −2)。

点 F 位于 x 轴上 x=3 处。点 F 的坐标为 (3,0)。

练习$\PageIndex{8}$

命名矩形坐标系中显示的每个点的有序对。

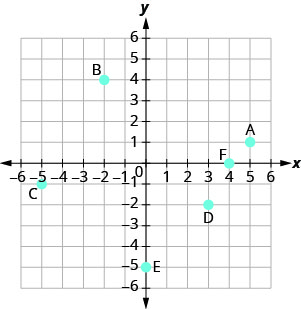
回答: A: (5,1) B: (−2,4) C: (−5, −1) D: (3, −2) E: (0, −5) F: (4,0)

练习$\PageIndex{9}$

命名矩形坐标系中显示的每个点的有序对。

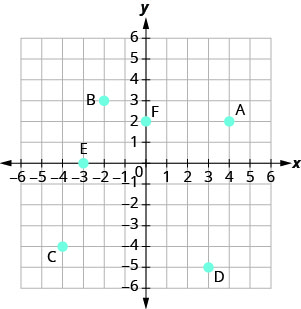
该图显示了 x y 坐标平面。 x 轴和 y 轴分别从负 6 到 6 不等。点（负 5、0）、（3、0）、（0、0）、（0、负 1）和（0、4）分别绘制并标记为 A、B、C、D 和 E。 — 图$\PageIndex{10}$

回答: A: (4,2) B: (−2,3) C: (−4, −4) D: (3, −5) E: (−3,0) F: (0,2)

验证两个变量中方程的解

到目前为止，你求解的所有方程都是只有一个变量的方程。在几乎所有情况下，当你求解方程时，你只得到了一个解。求解方程的过程以像 x=4 这样的语句结束。（然后，你用回方程来检查解。）

以下是一个变量中的方程及其一个解的示例。

\[\begin{aligned} 3 x+5 &=17 \\ 3 x &=12 \\ x &=4 \end{aligned}\]

但是方程可以有多个变量。具有两个变量的方程可以采用 Ax+By=C 的形式。这种形式的方程在两个变量中称为线性方程。

线性方程

Ax+By=C 形式的方程被称为两个变量的线性方程，其中 A 和 B 都不为零。

注意 line 这个词是线性的。以下是两个变量 x 和 y 中的线性方程的示例。

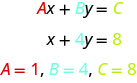
在此图中，我们可以看到线性方程 Ax plus By 等于 C。下方是方程 x 加 4y 等于 8。在此之下是值 A 等于 1，B 等于 4，C 等于 8。 — 图$\PageIndex{11}$

方程 y=−3x+5 也是一个线性方程。但它似乎不是 Ax+By=C 的形式。我们可以使用 Equality 的加法属性，然后以 Ax+By=C 的形式重写它。

$\begin{array}{llll} {} &{y} &{=} &{-3x + 5} \\ {\text{Add to both sides.}} &{y + 3x } &{=} &{-3x + 5 + 3x} \\{\text{Simplify.}} &{y + 3x} &{=} &{5} \\{\text{Use the Commutative Property to put it in}} &{3x + y} &{=} &{5} \\{Ax+By = C\text{ form.}} &{} &{} &{} \end{array}$

通过将 y=−3x+5 重写为 3x+y=5，我们可以很容易地看出它是由两个变量组成的线性方程，因为它的形式为 Ax+By=C。当方程的形式为 Ax+By=C 时，我们说它是标准形式。

线性方程的标准形式

线性方程在写成 Ax+By=C 时采用标准形式。

大多数人更喜欢将A、B和C作为整数，并且在以标准形式书写线性方程$A\geq 0$时，尽管这并不是绝对必要的。

线性方程有无限多的解。对于每个替换 x 的数字，都有一个对应的 y 值。这对值是线性方程的解，由有序对 (x, y) 表示。当我们将这些 x 和 y 的值代入方程时，结果是真实的陈述，因为左边的值等于右边的值。

两个变量中线性方程的解

有序对 (x, y) 是线性方程 Ax+By=C 的解，前提是当有序对的 x 和 y 值被替换为方程时，该方程为真陈述。

练习$\PageIndex{10}$

确定哪些有序对是方程 x+4y=8 的解。

(a) (0,2)

(b) (2, −4)

回答

将每个有序对中的 x 和 y 值替换到方程中，然后确定结果是否为真陈述。

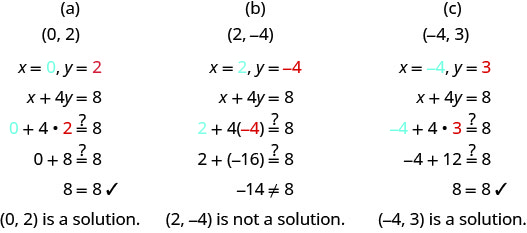
$此图有三列。第一列的顶部是有序对 (0, 2)。在此之下是值 x 等于 0，y 等于 2。下方是等式 x 加 4y 等于 8。下面是相同的方程，用 0 和 2 代替 x 和 y：0 加 4 乘以 2 可能等于 8。下方是 0 加 8 可能等于 8。下方是 8 等于 8，旁边有一个复选标记。下面是 “(0, 2) 是解决方案” 这句话。第二列的顶部是有序对（2，负 4）。在此之下是值 x 等于 2，y 等于负 4。下方是等式 x 加 4y 等于 8。下方是相同的方程，用 2 和负 4 代替 x 和 y：2 加 4 乘以负 4 可能等于 8。下方是 2 加负 16 可能等于 8。低于此值是负 14 不等于 8。下面是句子：“（2，负 4）不是解决方案。” 第三列的顶部是有序对（负 4、3）。在此之下是值 x 等于负 4，y 等于 3。下方是等式 x 加 4y 等于 8。下方是相同的方程，用负 4 和 3 代替 x 和 y：负 4 加 4 乘以 3 可能等于 8。下方是负数 4 加 12 可能等于 8。下方是 8 等于 8，旁边有一个复选标记。下面是句子：“（负数4，3）是一个解决方案。”$

练习$\PageIndex{11}$

以下哪个有序对是 2x+3y=6 的解？

(3,0)
(2,0)
(6, −2)

回答: 1、3

练习$\PageIndex{12}$

以下哪个有序对是方程 4x−y=8 的解？

(0,8)
(2,0)
(1, −4)

回答: 2、3

练习$\PageIndex{13}$

以下哪个有序对是方程 y=5x−1 的解？

(a) (0, −1)

(b) (1,4)

回答

将每个有序对中的 x 和 y 值替换到方程中，然后确定其结果是否为真。

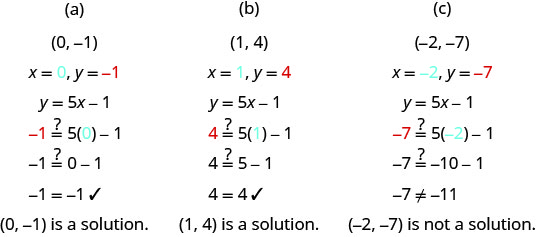
$此图有三列。第一列的顶部是有序对（0，负 1）。在此之下是值 x 等于 0，y 等于负 1。在此之下是方程 y 等于 5x 减去 1。下方是相同的方程，用 0 和负 1 代替 x 和 y：负 1 可能等于 5 倍 0 减去 1。下方是负数 1 可能等于 0 减去 1。下方是负 1 等于负 1，旁边有一个复选标记。下面是句子：“（0，负 1）是解。” 第二列的顶部是有序对 (1, 4)。在此之下是值 x 等于 1，y 等于 4。在此之下是方程 y 等于 5x 减去 1。下面是相同的方程，用 1 和 4 代替 x 和 y：4 可能等于 5 倍 1 减去 1。下方是 4 可能等于 5 减去 1。下方是 4 等于 4，旁边有一个复选标记。下面是句子：“（1，4）是一个解决方案。” 右列的顶部是有序对（负 2，负 7）。在此之下是值 x 等于负 2，y 等于负 7。在此之下是方程 y 等于 5x 减去 1。下面是用负 2 和负 7 代替 x 和 y 的相同方程：负 7 可能等于 5 乘以负 2 减去 1。下方是负 7 可能等于负 10 减去 1。低于此值是负 7 不等于负 11。下面是句子：“（负2，负 7）不是解决方案。”$

练习$\PageIndex{14}$

以下哪个有序对是方程 y=4x−3 的解？

(0,3)
(1,1)
(−1, −1)

回答: 2

练习$\PageIndex{15}$

以下哪个有序对是方程 y=−2x+6 的解？

(0,6)
(1,4)
(−2、−2)

回答: 1、2

完成两个变量中线性方程的解表

在上面的示例中，我们替换了给定有序对的 x 和 y 值，以确定它是否是线性方程的解。但是，如果没有给出订购的货币对，如何找到它们呢？这比你想象的要容易——你可以为 xx 选择一个值，然后求解 yy 的方程。或者，为 yy 选择一个值，然后求解 xx。

首先，我们来看看我们在练习中找到的方程 y = 5x−1 的解$\PageIndex{13}$。我们可以在解决方案表中总结这些信息，如表所示$\PageIndex{1}$。

桌子$\PageIndex{1}$
y=5x−1
x	y	(x, y)
0	−1	(0, −1)
1	4	(1,4)

要找到第三个解，我们让 x=2 求解 y。

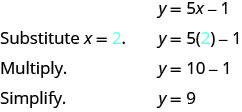
该图显示了在方程中 y 等于 5 x 减 1 时 x 等于 2 时求解 y 的步骤。方程 y 等于 5 x 减去 1 如图所示。其下方是用 2 代替 x 的方程，即 y 等于 5 乘以 2 减去 1。要求解 y，首先乘以使方程变成 y 等于 10 减去 1，然后减去方程 y 等于 9。 — 图$\PageIndex{12}$

有序对 (2,9) 是 y=5x−1 的解。我们会将其添加到表中$\PageIndex{2}$。

桌子$\PageIndex{2}$
y=5x−1
x	y	(x, y)
0	−1	(0, −1)
1	4	(1,4)
2	9	(2,9)

我们可以通过替换 x 的任意值或 y 的任意值，然后求解所得方程以得到另一个有序对即解，从而找到更多方程解。这个方程有无限多的解。

练习$\PageIndex{16}$

完成表以找出方程 y=4x−2 的三个解。

桌子$\PageIndex{3}$
y=4x−2
x	y	(x, y)
0
−1
2

回答

将 x=0、x=−1 和 x=2 替换为 y=4x−2。

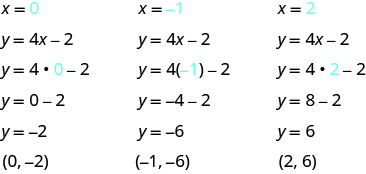
$此图有三列。第一列的顶部是值 x 等于 0。在此之下是方程 y 等于 4x 减去 2。下面是相同的方程，用 0 代替 x: y 等于 4 乘以 0 减去 2。下方是 y 等于 0 减去 2。下方是 y 等于负 2。在此之下是有序对（0，负 2）。第二列的顶部是值 x 等于负 1。在此之下是方程 y 等于 4x 减去 2。下方是相同的方程，用负 1 代替 x: y 等于 4 倍减去 1 减去 2。下方是 y 等于负 4 减去 2。下方是 y 等于负 6。在此之下是有序对（负 1，负 6）。第三列的顶部是值 x 等于 2。在此之下是方程 y 等于 4x 减去 2。下面是相同的方程，用 2 代替 x: y 等于 4 乘以 2 减去 2。下方是 y 等于 8 减去 2。在此之下是 y 等于 6。下方是有序对 (2, 6)。$

结果汇总在表中$\PageIndex{4}$。

桌子$\PageIndex{4}$
y=4x−2
x	y	(x, y)
0	−2	(0, −2)
−1	−6	(−1、−6)
2	6	(2,6)

练习$\PageIndex{17}$

填写表格以找到该方程的三个解：y=3x−1。

桌子$\PageIndex{5}$
y=3x−1
x	y	(x, y)
0
−1
2

回答

桌子$\PageIndex{6}$
y=3x−1
x	y	(x, y)
0	-1	(0, -1)
−1	-4	(-1、-4)
2	5	(2、5)

练习$\PageIndex{18}$

完成表格以找到该方程的三个解：y=6x+1。

桌子$\PageIndex{7}$
y=6x+1
x	y	(x, y)


-2

回答

桌子$\PageIndex{8}$
y=6x+1
x	y	(x, y)
0	1	(0,1)
1	7	(1,7)
−2	−11	(−2、−11)

练习$\PageIndex{19}$

填写表格$\PageIndex{9}$，找出方程 5x−4y=20 的三个解。

桌子$\PageIndex{9}$
5x−4y=20
x	y	(x, y)

	0
	5

回答

将给定值代入方程 5x−4y=20，然后求解另一个变量。然后，填写表中的值。

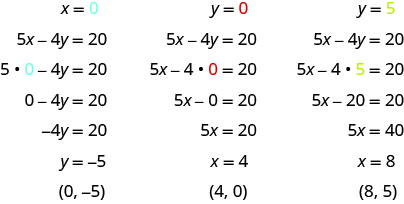
$此图有三列。第一列的顶部是值 x 等于 0。下方是等式 5x 减去 4y 等于 20。下面是相同的方程，用 0 代替 x：5 乘以 0 减去 4y 等于 20。下方是 0 减去 4y 等于 20。下方是负数 4y 等于 20。下方是 y 等于负 5。在此之下是有序对（0，负 5）。第二列的顶部是值 y 等于 0。下方是等式 5x 减去 4y 等于 20。下面是相同的方程，用 0 代替 y：5x 减去 4 倍 0 等于 20。下方是 5 倍减去 0 等于 20。低于这个值是 5 倍等于 20。下方是 x 等于 4。下方是有序对 (4, 0)。第三列的顶部是值 y 等于 5。下方是等式 5x 减去 47 等于 20。下面是相同的方程，用 5 代替 y：5x 减去 4 倍 5 等于 20。在此之下是等式 5x 减去 20 等于 20。低于这个值是 5 倍等于 40。下方是 x 等于 8。下方是有序对 (8, 5)。$

结果汇总在表中$\PageIndex{10}$。

桌子$\PageIndex{10}$
5x−4y=20
x	y	(x, y)
0	−5	(0, −5)
4	0	(4,0)
8	5	(8,5)

练习$\PageIndex{20}$

填写表格以找到该方程的三个解：2x−5y=20。

桌子$\PageIndex{11}$
2x−5y=20
x	y	(x, y)


-5

回答

桌子$\PageIndex{12}$
2x−5y=20
x	y	(x, y)
0	−4	(0, −4)
10	0	(10,0)
−5	−6	(−5、−6)

练习$\PageIndex{21}$

填写表格以找到该方程的三个解：3x−4y=12。

桌子$\PageIndex{13}$
3x−4y=12
x	y	(x, y)


-4

回答

桌子$\PageIndex{14}$
3x−4y=12
x	y	(x, y)
0	−3	(0, −3)
4	0	(4,0)
−4	−6	(−4、−6)

找到线性方程的解

要找到线性方程的解，你真的可以选择任何你想在方程中替换 x 或 y。但是由于你需要使用这个数字来求解另一个变量，所以选择一个易于使用的数字是个好主意。

当方程为 y 形式时，y 本身位于方程的一侧，通常更容易选择 x 的值然后求解 y。

练习$\PageIndex{22}$

找到方程 y=−3x+2 的三个解。

回答

我们可以用任何我们想要的值代替 x 或用任何值替换 y。由于方程是 y 形式，所以用 x 的值替换会更容易。让我们选择 x=0、x=1 和 x=−1。

			$。$	$。$	$。$
			$。$	$。$	$。$
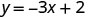
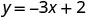
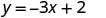
将该值替换到方程中。			$。$	$。$	$。$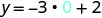
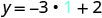
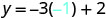
简化。			$。$	$。$	$。$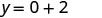
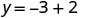
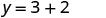
简化。			$。$	$。$	$。$
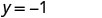
写下有序对。			(0, 2)	(1, -1)	(-1、5)
查看。
y=−3x+2	y=−3x+2	y=−3x+2
$2 \stackrel{?}{=} -3 \cdot 0 + 2$	$-1 \stackrel{?}{=} -3 \cdot 1 + 2$	$5 \stackrel{?}{=} -3 (-1) + 2$
$2 \stackrel{?}{=} 0 + 2$	$-1 \stackrel{?}{=} -3 + 2$	$5 \stackrel{?}{=} -3 + 2$
$2 = 2\checkmark$	$-1 = -1\checkmark$	$5 = 5\checkmark$

桌子$\PageIndex{15}$

因此，(0,2)、(1, −1) 和 (−1,5) 都是 y=−3x+2 的解。我们在表中显示它们$\PageIndex{16}$。

桌子$\PageIndex{16}$
y=−3x+2
x	y	(x, y)
0	2	(0,2)
1	−1	(1, −1)
−1	5	(−1,5)

练习$\PageIndex{23}$

找到这个方程的三个解：y=−2x+3。

回答: 答案会有所不同。

练习$\PageIndex{24}$

找到这个方程的三个解：y=−4x+1。

回答: 答案会有所不同。

我们已经看到，使用零作为 x 的一个值可以轻松找到 y 的值。当方程为标准形式时，x 和 y 在方程的同一边，通常更容易的是，当 x=0 时先找到一个解，当 y=0 时找到第二个解，然后再找到第三个解。

练习$\PageIndex{25}$

找出方程 3x+2y=6 的三个解。

回答

我们可以用任何我们想要的值代替 x 或用任何值代替 y。由于方程是标准形式，所以我们先选择 x=0，然后选择 y=0，然后再找第三个点。

桌子$\PageIndex{17}$
$。$	$。$	$。$
			$。$	$。$	$。$
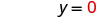
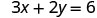
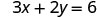
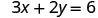
将该值替换到方程中。			$。$	$。$	$。$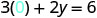
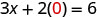
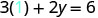
简化。			$。$	$。$	$。$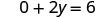
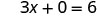
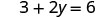
解决。			$。$	$。$	$。$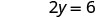
			$。$	$。$	$。$
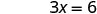
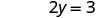
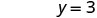
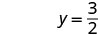
写下有序对。			(0, 3)	(2, 0)	$(1,\frac{3}{2})$
查看。
3x+2y=6	3x+2y=6	3x+2y=6
$3\cdot 0 + 2\cdot 3 \stackrel{?}{=} 6$	$3\cdot 2 + 2\cdot 0 \stackrel{?}{=} 6$	$3\cdot 1 + 2\cdot \frac{3}{2} \stackrel{?}{=} 6$
$0 + 6 \stackrel{?}{=} 6$	$6 + 0 \stackrel{?}{=} 6$	$3 + 3 \stackrel{?}{=} 6$
$6 = 6\checkmark$	$6 = 6\checkmark$	$6 = 6\checkmark$

所以 (0,3)、(2,0) 和$(1,\frac{3}{2})$都是方程 3x+2y=6 的解。我们可以在表中列出这三种解决方案$\PageIndex{18}$。

桌子$\PageIndex{18}$
3x+2y=63x+2y=6
x	y	(x, y)
0	3	(0,3)
2	0	(2,0)
1	$\frac{3}{2}$	$(1, \frac{3}{2})$

练习$\PageIndex{26}$

找出方程 2x+3y=6 的三个解。

回答: 答案会有所不同。

练习$\PageIndex{27}$

找出方程 4x+2y=8 的三个解。

回答: 答案会有所不同。

关键概念

象限的符号图案
$\begin{array}{ll}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}$
坐标轴上的点
- 在 x 轴上，y=0。 y 坐标等于 0 的点位于 x 轴上，并具有坐标 (a,0)。
- 在 y 轴上，x=0。 x 坐标等于 0 的点位于 y 轴上，并具有坐标 (0, b)。
线性方程的解
- 有序对 (x, y) 是线性方程 Ax+By=C 的解，前提是当有序对的 x 和 y 值被替换为方程时，该方程是正确陈述。

词汇表

线性方程: 线性方程的形式为 Ax+By=C，其中 A 和 B 不都为零，被称为两个变量中的线性方程。

已订购一对: 有序对 (x, y) 给出了矩形坐标系中点的坐标。

起源: 点 (0,0) (0,0) 被称为原点。它是 x 轴和 y 轴相交的点。

象限: x 轴和 y 轴将平面分成四个区域，称为象限。

矩形坐标系: 代数中使用网格系统来显示两个变量之间的关系；也称为 xy 平面或 “坐标平面”。

x 坐标: 有序对中的第一个数字 (x, y)。

y 坐标: 有序对中的第二个数字 (x, y)。

已订购对

起源

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

象限

坐标轴上的点

练习\(\PageIndex{4}\)

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

练习\(\PageIndex{9}\)

线性方程

线性方程的标准形式

两个变量中线性方程的解

练习\(\PageIndex{10}\)

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

练习\(\PageIndex{15}\)

练习\(\PageIndex{16}\)

练习\(\PageIndex{17}\)

练习\(\PageIndex{18}\)

练习\(\PageIndex{19}\)

练习\(\PageIndex{20}\)

练习\(\PageIndex{21}\)

练习\(\PageIndex{22}\)

练习\(\PageIndex{23}\)

练习\(\PageIndex{24}\)

练习\(\PageIndex{25}\)

练习\(\PageIndex{26}\)

练习\(\PageIndex{27}\)