3.3：求解混合物应用程序

Last updated
Save as PDF

Page ID: 204884

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

解决硬币字问题
解决票证和邮票字词问题
解决混词问题
使用混合模型使用单利率解决投资问题

注意

在开始之前，请参加这个准备测验。

乘以：$14(0.25)$。
如果您错过了此问题，请查看练习 1.8.19。
解决：$0.25x+0.10(x+4)=2.5$。
如果您错过了此问题，请查看练习 2.4.22。
一角钱比季度数多三角钱。假设 q 代表季度数。为硬币数写一个表达式。
如果您错过了此问题，请查看练习 1.3.43。

解决硬币单词问题

在混合问题中，我们将有两个或更多具有不同值的项目组合在一起。杂货商和调酒师使用混合模型来确保他们为所销售的产品设定公平的价格。许多其他专业人士，例如化学家、投资银行家和园艺师，也使用混合模型。

注意

进行操纵数学活动 Coin Lab 将帮助你更好地理解混词问题。

首先，我们将看一个每个人都熟悉的应用程序——金钱！

想象一下，我们从口袋或钱包里拿出少量硬币，然后放在桌子上。我们将如何确定那堆硬币的价值？如果我们能够制定分步计划来寻找硬币的总价值，那么在我们开始解决硬币词问题时，它将对我们有所帮助。

那我们该怎么办呢？为了顺序整理硬币，我们可以根据硬币的价值将硬币分成几堆。四分之一是四分之一，一角钱加一角钱，镍加镍，依此类推。为了获得所有硬币的总价值，我们将每堆硬币的总价值相加。

我们将如何确定每堆的价值？想想一大堆钱——它值多少钱？ 如果我们计算一角钱，我们就会知道我们有多少毛钱——一角钱。

但这并不能告诉我们所有硬币的价值。假设我们数了17毛钱，它们值多少钱？每角钱价值0.10美元，相当于一角钱的价值。要得出这堆17毛钱的总价值，请将17乘以0.10美元得出1.70美元。这是所有 17 角钱的总价值。此方法得出以下模型。

硬币的总价值

对于相同类型的硬币，许多硬币的总价值是通过使用模型得出的

\[number\cdot value = total\space value\]

其中，
数字是硬币的数量

价值是每枚硬币的价值

总价值是所有硬币的总价值

角钱数乘以每角钱的价值等于一角钱的总价值。

\[\begin{aligned} \text {number.} \cdot \text { value } &=\text { total value } \\ 17 \cdot \$ 0.10 &=\$ 1.70 \end{aligned}\]

我们可以继续对每种类型的硬币进行此处理，然后我们就会知道每种硬币的总价值。要获得所有硬币的总价值，请将每种硬币的总价值相加。

让我们来看一个具体案例。假设有 14 个季度、17 角钱、21 个镍和 39 个便士。

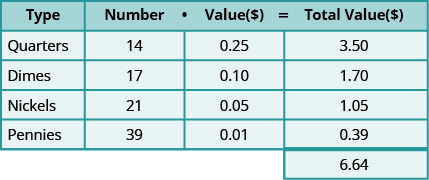
$此表有五行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行显示季度、14、0.25 和 3.50。第三行是 Dimes、17、0.10 和 1.70。第四行是 Nickels、21、0.05 和 1.05。第五行显示便士、39、0.01 和 0.39。额外的单元格读取 6.64。$

桌子$\PageIndex{1}$

所有硬币的总价值为6.64美元。

注意图表如何帮助整理所有信息！让我们看看我们如何使用这种方法来解决硬币字问题。

示例$\PageIndex{1}$

阿达尔贝托的口袋里有2.25美元的一角钱和镍。他的镍比一角钱多九个。他每种硬币有多少？

解决方案

第 1 步。 阅读问题。确保所有文字和想法都被理解。

确定所涉及的硬币类型。
想想我们用来寻找少量硬币价值的策略。我们需要做的第一件事是注意涉及哪些类型的硬币。阿达尔贝托有硬币和镍。 创建一个表来组织信息。见下图。

将列标记为 “类型”、“数字”、“值”、“总值”。
列出硬币的类型。
写下每种硬币的价值。
写下所有硬币的总价值。

我们可以用美分或美元来解决这个问题。在这里，我们将用美元进行操作，并在表格中输入美元符号（$）作为提醒。
一角钱的价值为0.10美元，镍的价值为0.05美元。所有硬币的总价值为2.25美元。下表显示了此信息。
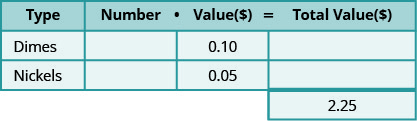
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行显示 “角钱”、“空白”、“0.10” 和 “空白”。第三行显示镍、空白、0.05 和空白。额外的单元格读取 2.25。$

第 2 步。 确定我们在寻找什么。

我们被要求找出阿达尔贝托拥有的硬币和镍的数量。

第 3 步。 说出我们要找的东西。选择一个变量来表示该数量。

使用变量表达式表示每种硬币的数量并将其写入表中。

将数字乘以该值得出每种硬币的总价值。

接下来我们计算了每种硬币的数量。在这个问题中，我们无法计算每种类型的硬币——这正是你要找的——但我们有一个线索。镍比硬币多九个。镍的数量比硬币的数量多九个。

\[\begin{aligned} \text { Let } d &=\text { number of dimes. } \\ d+9 &=\text { number of nickels } \end{aligned}\]

填写表格中的 “数字” 列以帮助整理所有内容。

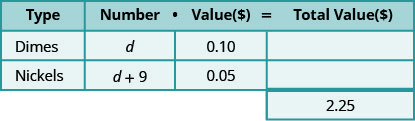
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行显示 “角钱”、“d”、“0.10” 和 “空白”。第三行是 Nickels、d 加 9、0.05 和空白。额外的单元格读取 2.25。$

现在我们有了问题所需的所有信息！

我们将数字乘以该值得出每种硬币的总价值。虽然我们不知道实际数字，但我们确实有一个表达式来表示它。

所以现在要乘以$\text{number}\cdot\text{value}=\text{total value}$。在下表中查看这是如何完成的。

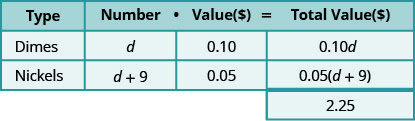
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行读取 “角钱”、“d”、“0.10” 和 “0.10d”。第三行读取 Nickels、d 加 9、0.05 和 0.05 乘以数量（d 加 9）。额外的单元格读取 2.25。$

请注意，我们让表格的标题显示了模型。

第 4 步。 翻译成方程式。用一句话重述问题可能会有所帮助。将英语句子翻译成代数方程。

通过将所有类型硬币的总值相加来写出方程式。

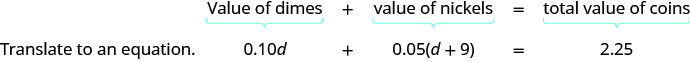
$“一角钱的价值加上镍的价值等于硬币的总价值” 这句话可以翻译成一个方程式。将 “一角钱的价值” 转换为0.10d，将 “镍的价值” 转换为0.05d，并将 “硬币的总价值” 转换为2.25。完整方程为 0.10d 加 0.05 乘以量 d 加 9 等于 2.25。$

第 5 步。使用良好的代数技巧求解方程。

现在求解这个方程。	$。$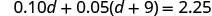
分发。	$。$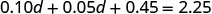
将相似的术语组合在一起。	$。$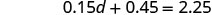
每边减去 0.45。	$。$
除以。	$。$
所以有 12 毛钱。
镍的数量为 d+9d+9。	$。$
	$。$
	21

第 6 步。 检查问题中的答案并确保答案合理。

这会检查吗？

\[\begin{array}{llll}{12 \text { dimes }} & {12(0.10)} &{=} &{1.20} \\ {21 \text { nickels }} & {21(0.05)} & {=} &{\underline{1.05}} \\ {} &{} &{}&{$ 2.25\checkmark} \end{array}\]

第 7 步。用完整的句子回答问题。

阿达尔贝托有十二角钱和二十一镍。

如果这是家庭作业练习，我们的工作可能如下所示。

$在带衬的活页纸上写的家庭作业。作业内容是：“阿达尔贝托的口袋里有2美元和25美分的毛钱和镍。他的镍比一角钱多九个。他每种类型有多少种？” 下面是一张表。表的第一行是标题行，每个单元格为其下方的一列或多列命名。左起第一个单元格被命名为 “类型”。第二个单元格包含等式 “数字” 乘以 “值” 等于 “总值”，其中一列对应 “数字”，一列对应 “值”，一列对应总值。因此，“数字” 列的内容乘以 “值” 列的内容等于 “总值” 列的内容。在表的第二行中，“类型” 列包含 “角钱”，“数字” 列包含 d，“值” 列包含 0.10，“总值” 列包含 0.10d。在表的第三行中，“类型” 列包含 “镍”，“数字” 列包含 d 加 9，“值” 列包含 0.05，“总值” 列包含数量 d 加 9 的 0.05 倍。向下一行，“总值” 列又包含一个单元格，其中包含 2.25。表下方是等式 0.10d 加 0.05d 加 0.45 等于 2.25。下方是 0.15d 加 0.45 等于 2.25。下方是 0.15d 等于 1.80。右边是 d 加 9，相当于 12 加 9 或 21 镍。右边是检查阶段，我们看看12毛钱和21个镍是否等于2美元和25美分。12倍0.10等于1.20，21倍（0.05）等于1.05。1.20加1.05等于2.25。$

试试看$\PageIndex{1}$

迈克尔拉的零钱包里有2.05美元的一毛钱和镍。她比镍多七角钱。她每种类型有多少枚硬币？

回答: 9 个镍，16 毛钱

试试看$\PageIndex{2}$

莉莉安娜的背包里有2.10美元的镍和四分之一的钱。她的镍比四分之一多 12 个。她每种类型有多少枚硬币？

回答: 17 个镍，5 个季度

解决硬币单词问题。

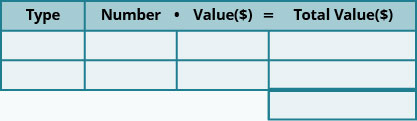
阅读问题。确保所有文字和想法都被理解。
- 确定所涉及的硬币类型。
- 创建一个表来组织信息。
- 将列标记为 “类型”、“数字”、“值”、“总值”。
- 列出硬币的类型。
- 写下每种硬币的价值。
- 写下所有硬币的总价值。
确定我们在寻找什么。
说出我们要找的东西。选择一个变量来表示该数量。
- 使用变量表达式表示每种硬币的数量并将其写入表中。
- 将数字乘以该值得出每种硬币的总价值。
翻译成方程式。
用一句话用所有重要信息重述问题可能会有所帮助。然后，将句子翻译成方程式。
通过将所有类型硬币的总值相加来写出方程式。
使用良好的代数技巧求@@ 解方程。
检查问题中的答案并确保答案合理。
用完整的句子@@ 回答问题。

示例$\PageIndex{2}$

玛丽亚每季度有2.43美元，钱包里有几分钱。她的便士是四分之一的两倍。她每种类型有多少枚硬币？

解决方案

第 1 步。 阅读问题。

确定所涉及的硬币类型。

我们知道玛丽亚有四分之一和便士。

创建一个表来组织信息。

第 2 步。 确定你在找什么。
- 我们正在寻找季度数和便士。
第 3 步。姓名。 使用变量表示季度数和便士数。
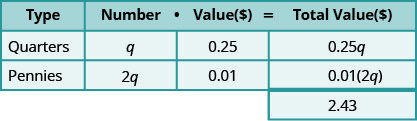
- 将 “数字” 和 “值” 相乘得出每种硬币的 “总价值”。 $没有替代文本$
  第 4 步。翻译。 通过将所有类型硬币的 “总价值” 相加来写出方程式。
  
  $\begin{array} {ll} {\textbf{Step5. Solve} \text{ the equation.}} &{0.25q + 0.01(2q) = 2.43} \\{\text{Multiply.}} &{0.25q + 0.02q = 2.43} \\ {\text{Combine like terms.}} &{0.27q = 2.43} \\ {\text{Divide by 0.27}} &{q = 9 \text{ quarters}} \\ {\text{The number of pennies is 2q.}} &{2q} \\ {} &{2\cdot 9} \\ {} &{18 \text{ pennies}} \\ {\textbf{Step 6. Check} \text{ the answer in the problem.}} &{} \\\\ {\text{Maria has 9 quarters and 18 pennies. Dies this}} &{} \\ {\text{make }$2.43?} &{} \end{array}$
  $\begin{array} {llll}\\ {9\text{ quarters }} &{ 9(0.25)} &{=} &{2.25} \\ {18\text{ pennies }} &{18(0.01)} &{=} &{\underline{0.18}} &{}\\ {\text{Total}} &{} &{} &{$2.43\checkmark} \end{array}$
  $\begin{array} {ll} \\ {\textbf{Step 7. Answer}\text{ the question.}} &{\text{Maria has nine quarters and eighteen pennies.}} \end{array}$

试试看$\PageIndex{3}$

苏曼塔的存钱罐里有4.20美元的镍和一角钱。她的镍是硬币的两倍。她每种类型有多少枚硬币？

回答: 42 个镍，21 毛钱

试试看$\PageIndex{4}$

艾莉森钱包里的一角钱是四分之一的三倍。她总共有9.35美元。她每种类型有多少枚硬币？

回答: 51 毛钱，17 个季度

在下一个示例中，我们将只显示已完成的表格——记住我们填写表格所采取的步骤。

示例$\PageIndex{3}$

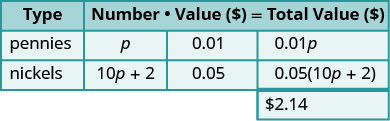
丹尼的存钱罐里有价值2.14美元的便士和镍。镍的数量是便士数量的十倍以上的两倍。丹尼有多少镍和多少便士？

解决方案

第 1 步。阅读问题。
确定所涉及的硬币类型。	便士和镍
创建表。
写下每种硬币的价值。	便士价值0.01美元。镍的价值0.05美元。
第 2 步。确定我们在寻找什么。	便士和镍的数量
第 3 步。姓名。使用变量表示每种硬币的数量。
镍的数量是根据便士的数量定义的，所以从便士开始。	让$p=$数便士。
镍的数量是便士数量的十倍以上的两倍。	再来看镍的$10p+2=$数量。
将数字和值相乘得出每种硬币的总价值。
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行读取便士、p、0.01 和 0.01p。第三行读取镍，10p 加 2、0.05 和 0.05 乘以数量（10 便士加 2）。额外的单元格读取2.14美元。$
第 4 步。翻译。通过将所有类型硬币的总价值相加来写出方程式。	$。$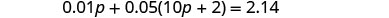
第 5 步。求解方程。	$。$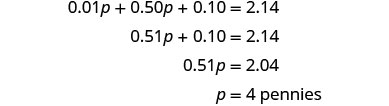
多少镍？	$。$
第 6 步。查看问题中的答案，确保 Danny 有四分钱和 42 个镍合理。总价值是2.14美元吗？ $\begin{array}{rll} {4(0.01)+42(0.05)} &{\stackrel{?}{=}} &{2.14} \\ {2.14} &{=} &{2.14\checkmark} \end{array}$
第 7 步。回答问题。	丹尼有四便士和 42 个镍。

试试看$\PageIndex{5}$

杰西口袋里有价值6.55美元的季度和镍。镍的数量是四分之一数的两倍以上的五个。杰西有多少镍和多少个季度？

回答: 41 个镍，18 个季度

试试看$\PageIndex{6}$

Elane 的硬币罐里总共有 7.00 美元的毛钱和镍。 Elane 拥有的硬币数量比镍的三倍少了七角钱。 Elane 每枚硬币有多少枚？

回答: 22 个镍，59 毛钱

解决票证和邮票字词问题

涉及门票或邮票的问题很像硬币问题。每种类型的票证和邮票都有价值，就像每种硬币一样。因此，为了解决这些问题，我们将遵循与解决硬币问题相同的步骤。

示例$\PageIndex{4}$

在学校音乐会上，售出的门票总价值为1,506美元。学生票每张售价为6美元，成人票每张售价为9美元。售出的成人票数量为五张，比售出的学生票数量少三倍。售出了多少张学生票和多少张成人票？

解决方案

第 1 步。 阅读问题。

确定涉及的门票类型。有学生票和成人票。
创建一个表来组织信息。

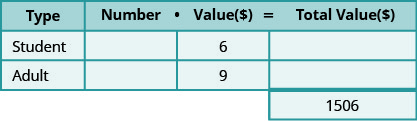
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行显示学生、空白、6 和空白。第三行显示成人、空白、9 和空白。额外的单元格读取 1506。$

第 2 步。 确定我们在寻找什么。

我们正在寻找学生和成人门票的数量。

第 3 步。姓名。 使用变量表示每种类型的票证的数量。

我们知道售出的成人票数量比售出的学生票数量少了五张。

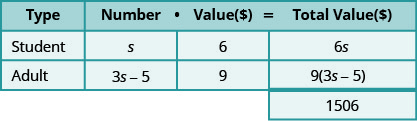
将数字乘以该值得出每种类型票证的总价值。 $此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行显示学生、s、6 和 6s。第三行显示成人，3s 减去数量 5、9 和 9 倍（3s 减去 5）。额外的单元格读取 1506。$
第 4 步。翻译。 通过将每种类型的票证的总值相加来写出方程式。

\[6 s+9(3 s-5)=1506 \nonumber\]

第 5 步。求解方程。

\[\begin{array}{rcl}{6 s+27 s-45} &{=} &{1506} \\ {33 s-45} &{=} &{1506} \\ {33 s} &{=} &{1551} \\ {s} & {=} &{47 \text { student tickets }} \\ {\text{Number of adult tickets}} &{=} &{3s-5} \\ {} &{=} &{3(47)-5} \\ {\text{So there were}} &{136} &{\text{adult tickets}}\end{array} \nonumber\]

第 6 步。 检查答案。

共有47张学生票，每张6美元，还有136张成人票，每张9美元。总价值是1,506美元吗？我们通过将门票数量乘以其价值来得出每种类型门票的总价值，然后相加得出所有售出门票的总价值。

\[\begin{array}{lll} {47\cdot 6} &{=} &{282} \\ {136\cdot 9} &{=} &{\underline{1224}} \\ {} &{} &{1506\checkmark} \\\end{array} \nonumber\]

第 7 步。 回答问题。他们售出了47张学生票和136张成人票。

试试看$\PageIndex{7}$

水球锦标赛的第一天，售出的门票总价值为17,610美元。一日通行证售价为20美元，锦标赛通行证售价为30美元。售出的锦标赛通行证数量比售出的日间通行证数量多37张。售出了多少日通行证和多少张锦标赛通行证？

回答: 330 张日通行证，367 张锦标赛通行证

试试看$\PageIndex{8}$

在电影院，售出的门票总价值为2,612.50美元。成人票每张售价为10美元，老年人/儿童票每张售价为7.50美元。售出的老年人/儿童票数量为25张，少于售出成人票数量的两倍。售出了多少张老年人/儿童票和多少张成人票？

回答: 112 张成人票，199 张老年人/儿童票

我们已经学会了当一种类型的门票的数量基于另一种类型的门票的数量时如何找到总票数。接下来，我们来看一个例子，在这个例子中，我们知道门票的总数，并且必须弄清楚这两种类型的票证是如何关联的。

假设比安卡总共卖出了 100 张门票。每张票要么是成人票，要么是儿童票。如果她卖了 20 张儿童票，那么她卖了多少张成人票？

你刚才说 “80”？你是怎么知道的？你从 100 中减去了 20 吗？

如果她卖了 45 张儿童票，那么她卖了多少张成人票？

你说'55'了吗？你是怎么找到的？从 100 中减去 45？

如果她卖了 75 张儿童票怎么办？她卖了多少张成人票？

成人票的数量必须为 100−75。她卖出了 25 张成人票。

现在，假设比安卡卖出了 x 张儿童票。那她卖了多少张成人票？为了找出答案，我们将遵循上面使用的相同逻辑。在每种情况下，我们从 100 张中减去儿童票的数量得出成人票的数量。我们现在对 x 做同样的事情。

我们在下面对此进行了总结。

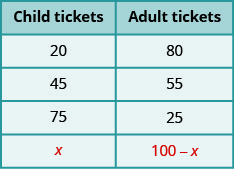
$此表有五行两列。第一行是标题行，从左到右显示儿童票和成人票。第二行读取 20 和 80。第三行读取 45 和 55。第四行读取 75 和 25。第五行读取 x 和 100 加 x。$

桌子$\PageIndex{2}$

我们可以将这些技术应用于其他示例

示例$\PageIndex{5}$

盖伦售出了810张教堂狂欢节门票，总额为2,820美元。儿童票每张3美元，成人票每张5美元。他卖了多少张儿童票和多少张成人票？

解决方案

第 1 步。 阅读问题。

确定涉及的门票类型。有儿童票和成人票。
创建一个表来组织信息。

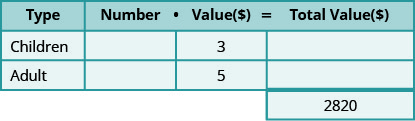
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行显示孩子、空白、3 和空白。第三行显示成人、空白、5 和空白。额外的单元格读取 2820。$

第 2 步。 确定我们在寻找什么。

我们正在寻找儿童和成人门票的数量。

第 3 步。姓名。 使用变量表示每种类型的票证的数量。

我们知道售出的门票总数为810张。
这意味着儿童票的数量加上成人票的数量必须加起来为 810。
假$c$设儿童票的数量。

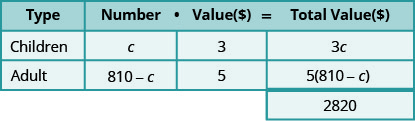
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行显示孩子、c、3 和 3c。第三行显示成人，810 减去 c、5 和 5 乘以数量（810 减去 c）。额外的单元格读取 2820。$

然后$810−c$是成人票的数量。
将数字乘以该值得出每种类型票证的总价值。

第 4 步。翻译。

通过将每种类型的票证的总值相加来写出方程式。

第 5 步。求解方程。

\[\begin{align*} 3 c+5(810-c) &=2,820 \\ 3 c+4,050-5 c &=2,820 \\-2 c &=-1,230 \\ c &=615 \text { children tickets } \end{align*}\]

有多少成年人？

\[\begin{array}{c}{810-c} \\ {810-615} \\ {195 \text { adult tickets }}\end{array} \nonumber\]

第 6 步。 检查答案。共有615张儿童票，每张3美元，还有195张成人票，每张5美元。总价值是2,820美元吗？

\[\begin{array}{rrl}{615 \cdot 3} &{=} & {1845} \\ {195 \cdot 5} &{=} & {\underline{975}} \\ {} &{} &{2,820\checkmark} \end{array} \nonumber\]

第 7 步。 回答问题。盖伦售出了 615 张儿童票和 195 张成人票。

试试看$\PageIndex{9}$

在博物馆售票亭轮班期间，莉亚售出了115张门票，总额为1,163美元。成人票价格为12美元，学生票为5美元。 Leah 卖了多少张成人票和多少张学生票？

回答: 84 张成人票，31 张学生门票

试试看$\PageIndex{10}$

一艘观鲸船上有 40 名付费乘客。从门票中收取的总金额为1,196美元。全价乘客每人支付32美元，减价乘客每人支付26美元。船上有多少全价乘客和多少减价乘客？

回答: 26 张全额票价，14 张减价票价

现在，我们来做一个一次性填写所有表格的工作。

示例$\PageIndex{6}$

莫妮卡花了8.36美元购买了邮票。 41美分邮票的数量是两美分邮票数量的两倍多四张。莫妮卡买了多少张 41 美分的邮票和多少张两美分的邮票？

解决方案

邮票的类型是41美分的邮票和2美分的邮票。他们的名字也赋予了价值！

“41美分邮票的数量是两美分邮票数量的两倍多四张。”

\[\begin{array}{l}{\text { Let } x=\text { number of } 2 \text { -cent stamps. }} \\ {2 x+4=\text { number of } 41-\text { cent stamps }}\end{array} \nonumber\]

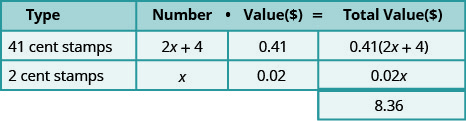
$此表有三行四列，第四列底部有一个额外的单元格。第一行是标题行，从左到右读取 “类型”、“数字”、“值” ($) 和 “总值 ($)”。第二行是 41 美分的邮票，2 倍加 4、0.41 和 0.41 乘以数量（2x 加 4）。第三行是 2 美分的邮票，分别是 x、0.02 和 0.02x。额外的单元格读取 8.36。$

\[\begin{array}{lr} {\text{Write the equation from the total values.}} &{0.41(2x + 4) + 0.02x = 8.36} \\ {} &{0.82x + 1.64 + 0.02x = 8.36} \\ {} &{0.84x + 1.64 = 8.36} \\ {\text{Solve the equation.}} &{0.84x = 6.72} \\ {} &{x = 8} \\\\ {\text{Monica bought eight two-cent stamps.}} &{} \\{\text{Find the number of 41-cent stamps she bought}} &{2x + 4 \text{ for } x = 8} \\{\text{by evaluating}} &{2x + 4} \\{} &{2(8) + 4} \\ {} &{20} \end{array} \nonumber\]

查看。

\[\begin{array} {rll} {8(0.02) + 20(0.41)} &{\stackrel{?}{=}} &{8.36} \\ {0.16 + 8.20} &{\stackrel{?}{=}} &{8.36} \\{8.36} &{=} &{8.46\checkmark} \end{array}\]
\[\begin{array} {ll} \\ {} &{\text{Monica bought eight two-cent stamps and 20}} \\ {} &{\text{41-cent stamps}} \end{array} \nonumber\]

试试看$\PageIndex{11}$

埃里克花了13.36美元购买了邮票。 41美分邮票的数量为八张，是两美分邮票数量的两倍多。埃里克买了多少张 41 美分的邮票和多少张两美分的邮票？

回答: 32 美元为 0.41 美元，12 美元为 0.02 美元

试试看$\PageIndex{12}$

Kailee 花了 12.66 美元购买了邮票。 41美分邮票的数量比20美分邮票数量少了四倍。凯莉买了多少张 41 美分的邮票和多少 20 美分的邮票？

回答: 26 美元为 0.41 美元，10 美元为 0.20 美元

解决混词问题

现在，我们将解决混合模型的一些更常见的应用。杂货商和调酒师使用混合模型为混合两种或更多原料制成的产品设定合理的价格。理财规划师在将资金投资于各种账户并想要找到总体利率时使用混合模型。景观设计师在有各种各样的植物和固定预算时使用混合模型，而活动协调员在为宴会选择开胃菜和主菜时也这样做。

我们的第一个混合词问题是用葡萄干和坚果制作混合物。

示例$\PageIndex{7}$

Henning 正在将葡萄干和坚果混合在一起，制成 10 磅的混合物。葡萄干每磅花费2美元，坚果每磅6美元。如果亨宁想把混合葡萄干的成本定为每磅5.20美元，那么他应该用多少磅的葡萄干和多少磅的坚果？

解决方案

和以前一样，我们填写一张图表来整理我们的信息。

10 磅的混合物将来自葡萄干和坚果的混合。

\[\begin{array}{l}{\text { Let } x=\text { number of pounds of raisins. }} \\ {10-x=\text { number of pounds of nuts }}\end{array} \nonumber\]

我们输入每件商品的每磅价格。

我们将数字乘以该值得出总值。

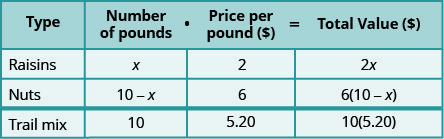
$此表有四行四列。第一行是标题行，从左至右显示类型、磅数、每磅价格 ($) 和总价值 ($)。第二行读取葡萄干 x、2 和 2x。第三行读取坚果，10 减去 x，6 和 6 乘以数量（10 减去 x）。第四行读取 trail mix，10、5.20 和 10 倍 5.20。$

请注意，表中的最后一行提供了混合物总量的信息。

我们知道葡萄干的价值加上坚果的价值将是混合葡萄干的价值。

从总值中写出方程。	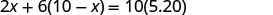$示例 3.32.jpg$
求解方程。	$。$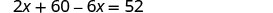
	$。$
	$。$
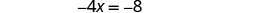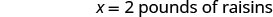找出坚果的磅数。	$。$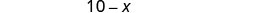
	$。$
	8 磅坚果
查看。 $\begin{array}{rll} {2($2) + 8($6)} &{\stackrel{?}{=} } &{10($5.20)} \\ {$4 + $48} &{\stackrel{?}{=} } &{$52} \\ {$52} &{=} &{$52\checkmark} \end{array}$
	亨宁将两磅葡萄干和八磅坚果混合在一起。

试试看$\PageIndex{13}$

奥兰多正在混合坚果和麦片方块来制作派对混合物。坚果的售价为每磅7美元，谷物方块的售价为每磅4美元。奥兰多想以每磅 6.50 美元的价格制作 30 磅的派对混合物，他应该用多少磅的坚果和多少磅的麦片方块？

回答: 5 磅麦片方块，25 磅坚果

试试看$\PageIndex{14}$

Becca 想混合果汁和苏打水来打一拳。她可以以每加仑3美元的价格购买果汁，以每加仑4美元的价格购买苏打水。如果她想以每加仑3.25美元的价格制作28加仑的拳头，那么她应该买多少加仑的果汁和多少加仑的苏打水？

回答: 21 加仑的水果饮料，7 加仑的苏打水

我们还可以使用混合模型使用单息来解决投资问题。我们使用了简单利率公式$I=Prt$，其中$t$表示年数。当我们只需要找到一年的利息时$t=1$，那就这样吧$I=Pr$。

示例$\PageIndex{8}$

Stacey 有 20,000 美元可以投资两个不同的银行账户。一个账户每年支付3％的利息，另一个账户按每年5％的利息支付。如果她想从总金额中赚取每年4.5％的利息，她应该在每个账户中投资多少钱？

解决方案

我们将填写一张图表来整理我们的信息。我们将使用简单利息公式来计算在不同账户中赚取的利息。

混合投资的利息将来自于将收入3％的账户的利息和收入5％的账户的利息相加，得出20,000美元的总利息。

\[\begin{aligned} \text { Let } x &=\text { amount invested at } 3 \% \\ 20,000-x &=\text { amount invested at } 5 \% \end{aligned}\]

投资金额是每个账户的本金。

我们输入每个账户的利率。

我们将投资金额乘以利率得出利息。

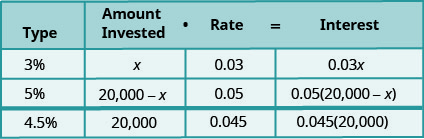
$此表有四行四列。第一行是标题行，从左到右显示类型、投资金额、利率和利息。第二行读取 3%、x、0.03 和 0.03x。第三行读取 5%、20,000 减去 x、0.05 和 0.05 乘以数量（20,000 减去 x）。第四行读取 4.5%、20,000、0.045 和 0.045 乘以 20,000。$

请注意，总投资金额为20,000美元，是投资金额为3％和投资金额为5％的总和。而总利息是3％账户中赚取的利息和5％账户中赚取的利息之和。$0.045(20,000)$

与其他混合应用一样，表中的最后一列为我们提供了要求解的方程。

用所得利息写出方程式。求解方程。	$\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}$
找出投资金额为5％。	$。$ $。$ $。$
查看。 $\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}$
	Stacey应该在收入为3％的账户中投资5,000美元，在收入为5％的账户中投资15,000美元。

试试看$\PageIndex{15}$

雷米有14,000美元可以投资两个共同基金。一个基金每年支付4％的利息，另一个基金按每年7％的利息支付。如果她想赚取总额6.1％的利息，她应该在每只基金中投资多少？

回答: 4,200 美元 4%，9,800 美元，7%

试试看$\PageIndex{16}$

Marco 有 8,000 美元可以存钱用于女儿的大学教育。他想将其分为一个每年支付3.2％利息的账户和另一个每年支付8％利息的账户。如果他希望总投资的利息达到6.5％，他应该在每个账户中投资多少？

回答: 2,500 美元，3.2％，5,500 美元，8％

关键概念

硬币的总价值对于相同类型的硬币，使用模型可以找到许多硬币的总价值。
number·value=总价值，其中数字是硬币的数量，价值是每枚硬币的价值；总价值是所有硬币的总价值
问题解决策略—硬币词问题
1. 阅读问题。让所有的文字和想法都被理解。确定所涉及的硬币类型。
  - 创建一个表来组织信息。
  - 标记列类型、数字、值、总值。
  - 列出硬币的类型。
  - 写下每种硬币的价值。
  - 写下所有硬币的总价值。
2. 确定我们在寻找什么。
3. 说出我们要找的东西。选择一个变量来表示该数量。
  使用变量表达式表示每种硬币的数量并将其写入表中。
  将数字乘以该值得出每种硬币的总价值。
4. 翻译成方程式。用一句话用所有重要信息重述问题可能会有所帮助。然后，将句子翻译成方程式。
  通过将所有类型硬币的总值相加来写出方程式。
5. 使用良好的代数技巧求@@ 解方程。
6. 检查问题中的答案并确保答案合理。
7. 用完整的句子@@ 回答问题。

词汇表

混合物问题: 混合问题将两个或多个具有不同值的项目组合在一起。

用所得利息写出方程式。求解方程。	\(\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}\)
找出投资金额为5％。	$。$ $。$ $。$
查看。 \(\begin{array}{rll} {0.03x + 0.05(15000 + x)} &{\stackrel{?}{=} } &{0.045(20000)} \\ {150 + 750} &{\stackrel{?}{=} } &{900} \\ {900} &{=} &{900\checkmark} \end{array}\)
	Stacey应该在收入为3％的账户中投资5,000美元，在收入为5％的账户中投资15,000美元。

注意

硬币的总价值

示例\(\PageIndex{1}\)

试试看\(\PageIndex{1}\)

试试看\(\PageIndex{2}\)

解决硬币单词问题。

示例\(\PageIndex{2}\)

试试看\(\PageIndex{3}\)

试试看\(\PageIndex{4}\)

示例\(\PageIndex{3}\)

试试看\(\PageIndex{5}\)

试试看\(\PageIndex{6}\)

示例\(\PageIndex{4}\)

试试看\(\PageIndex{7}\)

试试看\(\PageIndex{8}\)

示例\(\PageIndex{5}\)

试试看\(\PageIndex{9}\)

试试看\(\PageIndex{10}\)

示例\(\PageIndex{6}\)

试试看\(\PageIndex{11}\)

试试看\(\PageIndex{12}\)

示例\(\PageIndex{7}\)

试试看\(\PageIndex{13}\)

试试看\(\PageIndex{14}\)

示例\(\PageIndex{8}\)

试试看\(\PageIndex{15}\)

试试看\(\PageIndex{16}\)