3.1: 使用问题解决策略

Last updated
Save as PDF

Page ID: 204800

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

学习目标

在本节结束时，您将能够：

以积极的态度处理单词问题
对单词问题使用问题解决策略
解决数字问题

注意

在开始之前，请参加这个准备测验。

将 “6 小于两倍 x” 翻译成代数表达式。
如果您错过了此问题，请查看练习 1.3.43。
解决：$\frac{2}{3}x=24$。
如果您错过了此问题，请查看练习 2.2.10。
解决：$3x+8=14$。
如果您错过了此问题，请查看练习 2.3.1。

以积极的态度处理单词问题

“如果你认为可以... 或者认为你做不到... 你是对的。” —亨利·福特

这个世界充满了文字问题！我的收入有资格租那套公寓吗？我需要为派对打多少拳头？我能买多大尺寸的钻石给我的女朋友？我应该乘飞机还是开车去与家人团聚？我需要多少钱才能给车加油？我应该在餐厅留多少小费？度假时我应该带多少只袜子？感恩节晚餐我需要买多大尺寸的火鸡，然后我需要什么时候把它放进烤箱里？如果我和姐姐给妈妈买礼物，我们每个人要付多少钱？

现在我们可以求解方程了，我们已经准备好将我们的新技能应用于单词问题了。你认识过去有过文字问题负面经历的人吗？你有过像下面的学生一样的想法吗（图$\PageIndex{1}$）？

学生会看到一个思想泡泡说：“我不知道该加、减、乘还是除！，” “我不明白单词问题！，” “我的老师从来没有解释过这个！，” “如果我跳过所有问题这个词，我可能还能通过课程” 和 “我就是做不到！” — 图$\PageIndex{1}$：消极的想法可能成为成功的障碍。

当我们觉得自己无法控制并继续重复消极想法时，我们就会为成功设置障碍。我们需要平息恐惧，改变我们的负面情绪。

从一个全新的角度开始，开始思考积极的想法。如果我们控制住并相信自己能取得成功，我们就能掌握单词问题！阅读 Figure 中的积极想法$\PageIndex{2}$，然后大声说出来。

一个学生被带着思想泡泡说：“虽然过去单词问题很难，但我想我现在可以尝试了”，“我现在准备得更好了。我想我会开始理解单词问题了，” “我想我可以！我想我可以！，” 和 “这可能需要时间，但我可以开始解决单词问题了。” — 图$\PageIndex{2}$：思考积极的想法是迈向成功的第一步。

想一想，在校外，你现在可以做但三年前做不到的事情。它在开车吗？单板滑雪？做一顿美味的饭菜？说一门新语言？你过去遇到单词问题的经历发生在你年轻的时候，现在你已经年纪大了，准备好取得成功！

对单词问题使用问题解决策略

我们已经回顾了使用一些基本的数学词汇和符号将英语短语翻译成代数表达式的情况。我们还将英语句子翻译成代数方程并解决了一些单词问题。问题这个词将数学应用于日常情况。我们用一句话重述了情况，赋了一个变量，然后写了一个方程来解决问题。只要情况熟悉并且数学不太复杂，这种方法就行得通。

现在，我们将扩展我们的策略，以便我们可以使用它来成功解决任何单词问题。我们将在这里列出策略，然后用它来解决一些问题。我们在下面总结了解决问题的有效策略。

使用问题解决策略来解决单词问题。

阅读问题。确保所有文字和想法都被理解。
确定我们在寻找什么。
说出我们要找的东西。选择一个变量来表示该数量。
翻译成方程式。用一句话用所有重要信息重述问题可能会有所帮助。然后，将英语句子翻译成代数方程。
使用良好的代数技巧求@@ 解方程。
检查问题中的答案并确保答案合理。
用完整的句子@@ 回答问题。

练习$\PageIndex{1}$

皮拉尔买了一个钱包出售$$18$，这是原价的一半。钱包的原价是多少？

回答

第 1 步。 阅读问题。如有必要，请阅读问题两次或多次。在字典或互联网上查找任何不熟悉的单词。

在这个问题中，讨论的内容是否清楚？每个字都熟悉吗？

假设 p = 钱包的原始价格。

第 2 步。 确定你在找什么。你有没有去卧室去买东西然后忘记自己在找什么？如果你不确定它是什么，就很难找到东西！再读一遍问题并寻找能告诉你你在找什么的词语！

在这个问题中，“钱包的原价是多少” 这句话告诉我们我们需要找到什么。

第 3 步。 说出我们要找的东西。选择一个变量来表示该数量。我们可以使用任何字母作为变量，但要选择一个便于记住它所代表的内容的字母。

第 4 步。 翻译成方程式。用一句话用所有重要信息重述问题可能会有所帮助。将英语句子翻译成代数方程。

仔细阅读问题以了解给定信息之间的关系。通常，有一句话可以提供这些信息，或者写一句包含所有重要信息的句子可能会有所帮助。寻找线索词以帮助将句子翻译成代数。将句子翻译成方程式。

用一句话用所有重要信息重述问题。	$\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}$
翻译成方程式。	$18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p$

第 5 步。使用良好的代数技巧求解方程。即使你马上就知道了解决方案，在这里使用好的代数技巧也可以更好地为解决没有明显答案的问题做好准备。

求解方程。	$18 = \frac{1}{2}p$
将两边乘以 2。	$ {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p $
简化。	$36 = p$

第 6 步。 检查问题中的答案以确保答案合理。我们求解了方程式后发现$p=36$，这意味着 “原始价格” 是$$36$。

这个问题36美元有意义吗？是的，因为18是36个的一半，而钱包的售价是原价的一半。

如果这是一次家庭作业，我们的工作可能看起来像这样：

皮拉尔买了一个钱包出售$$18$，这是原价的一半。钱包的原价是多少？

第 7 步。用完整的句子回答问题。问题问道：“钱包的原价是多少？”

这个问题的答案是：“钱包的原价是36美元。”

	让$p =$原价出发。
	$18$是原价的一半。
	$18 = \frac{1}{2}p$
将两边乘以$2$。	$ {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p $
简化。	$36 = p$
查看。钱包的价格合理吗？$$36$
是的。
$18$一半是$36$吗？
$18 \stackrel{?}{=} \frac{1}{2}\cdot 36$
$18 = 18\checkmark$
	钱包的原价是$$36$。

练习$\PageIndex{2}$

华金以出售的价格购买了一个书柜$$120$，这是原价的三分之二。书柜的原价是多少？

回答: $$180$

练习$\PageIndex{3}$

Mariel播放列表中五分之二的歌曲是乡村歌曲。如果有$16$乡村歌曲，播放列表中的歌曲总数是多少？

回答: $40$

让我们用另一个例子来试试这个方法。

练习$\PageIndex{4}$

金妮和她的同学组成了一个学习小组。研究组中的女生人数为三人，是男生人数的两倍多。研究组里有$11$女生。研究组中有多少男孩？

回答

第 1 步。阅读问题。
第 2 步。确定我们在寻找什么。	研究组中有多少男孩？
第 3 步。姓名。选择一个变量来表示男孩的数量。	假$n=$设男孩的数量。
第 4 步。翻译。用一句话用所有重要信息重述问题。	$\color{cyan} \underbrace{\color{black}\textbf{The number}\\ \color{black}\textbf{of girls}(11)} \quad \underbrace{\strut \text{ } \\ \color{black}\textbf{was}} \quad \underbrace{\color{black}\textbf{three more than}\\ \color{black}\textbf{twice the number of boys}}$
翻译成方程式。	$\qquad 11 \qquad \quad = \qquad \qquad \quad 2b + 3$
第 5 步。求解方程。	$\quad 11 = 2b + 3 $
每边减去 3。	$\quad 11 \,{\color{red}{- \,3}} = 2b + 3 \,{\color{red}{- \,3}} $
简化。	$\quad 8 = 2b $
将每边除以 2。	$ \quad \dfrac{8}{\color{red}{2}}=\dfrac{2b}{\color{red}{2}} $
简化。	$\quad 4 = b$
第 6 步。查看。首先，我们的答案合理吗？是的，让$4$男孩加入学习小组似乎还可以。问题是说女孩的数量是男孩人数的两倍$3$多。如果有四个男孩，那就等于十一个女孩吗？ $4$男孩是两次$8$。比$8$现在多了三个$11$。
第 7 步。回答问题。	研究组里有$4$男孩。

练习$\PageIndex{5}$

吉列尔莫在书店买了教科书和笔记本。教科书的数量是笔记本数量的两倍$3$多。他买了$7$教科书。他买了多少本笔记本电脑？

回答: $2$

练习$\PageIndex{6}$

Gerry 本周制作了数独谜题和填字游戏。他完成的数独谜题数量是填字游戏数量的两倍多八个。他完成了$22$数独谜题。他做了多少填字游戏？

回答: $7$

解决数字问题

现在我们有了解决问题的策略，我们将在几种不同类型的单词问题上使用它。我们将研究的第一种类型是 “数字问题”。数字问题提供了有关一个或多个数字的一些线索。我们用这些线索来写一个方程式。数字问题通常不是每天都会出现，但它们为练习上述问题解决策略提供了很好的介绍。

练习$\PageIndex{7}$

数字和六的差异是$13$。找到号码。

回答

第 1 步。阅读问题。所有的词都熟悉吗？
第 2 步。确定我们在寻找什么。	这个数字
第 3 步。姓名。选择一个变量来表示数字。	让$n=$数字来。
第 4 步。翻译。记得找一些线索词，比如 “差异... of... 和...”
用一句话重述问题。	$\color{cyan} \underbrace{\color{black}\textbf{The difference of the number and }\mathbf{6}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\strut \color{black}\mathbf{13}}$
翻译成方程式。	$\qquad \qquad \qquad n-6 \qquad \qquad \qquad \quad = \quad 13$
第 5 步。求解方程。	$\quad n - 6 = 13$
简化。	$\quad n =19$
第 6 步。查看。
$19$和的区别$6$是$13$。它会检查！
第 7 步。回答问题。	数字是$19$。

练习$\PageIndex{8}$

数字和八的差异是$17$。找到号码。

回答: $25$

练习$\PageIndex{9}$

数字和十一的差异是$−7$。找到号码。

回答: $4$

练习$\PageIndex{10}$

两个数字和七的总和是$15$。找到号码。

回答

第 1 步。阅读问题。
第 2 步。确定我们在寻找什么。	这个数字
第 3 步。姓名。选择一个变量来表示数字。	让$n =$数字来。
第 4 步。翻译。
用一句话重述问题。	$。$
翻译成方程式。	$。$
第 5 步。求解方程。	$。$
每边减去 7 然后简化。	$。$
将每边除以 2 然后简化。	$。$
第 6 步。查看。
两次 4 和 7 的总和等于 15 吗？
$\begin{array} {rrl} {2\cdot 4 + 7} &{\stackrel{?}{=}}& {15} \\ {15} &{=} &{15\checkmark} \end{array}$
第 7 步。回答问题。	数字是$4$。

你有没有注意到我们在求解这个方程式时遗漏了一些步骤？如果您还没有准备好省略这些步骤，请根据需要写下任意数量的步骤。

练习$\PageIndex{11}$

四乘以一个数字和二的总和是$14$。找到号码。

回答: $3$

练习$\PageIndex{12}$

三乘以一个数字和七的总和是$25$。找到号码。

回答: $6$

一些数字词问题要求我们找到两个或多个数字。用不同的变量命名它们可能很诱人，但是到目前为止，我们只用一个变量求解了方程。为了避免使用多个变量，我们将根据同一个变量定义数字。一定要仔细阅读问题，以了解所有数字之间的关系。

练习$\PageIndex{13}$

一个数字比另一个数字多五个。数字之和为 21。找到数字。

回答

第 1 步。阅读问题。
第 2 步。确定我们在寻找什么。		我们正在寻找两个数字。
第 3 步。姓名。我们有两个数字要命名，每个数字都需要一个名字。
选择一个变量来表示第一个数字。		让我们$n=1^{st}$编号。
我们对第二个数字了解多少？		一个数字比另一个数字多五个。
		$n+5=2^{nd}$数字
第 4 步。翻译。将问题重述为一句话，其中包含所有重要信息。		第 1 个数字和^第 2 个数字之^和为 21。
翻译成方程式。		$。$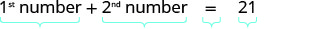
替换变量表达式。		$。$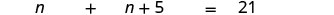
第 5 步。求解方程。		$。$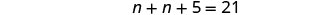
将相似的术语组合在一起。		$。$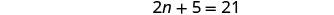
从两边减去 5 然后简化。		$。$
除以 2 然后简化。		$。$
也要找到第二个数字。		$。$
		$。$
		$。$
第 6 步。查看。
这些数字能解决问题吗？
一个数字$5$比另一个数字多吗？	$13\stackrel{?}{=} 8 + 5$
比十三$5$多$8$吗？是的。	$13 = 13\checkmark$
是两个数字的总和$21$吗？	$8 + 13 \stackrel{?}{=} 21$
	$21 = 21\checkmark$
第 7 步。回答问题。		数字是$8$和$13$。

练习$\PageIndex{14}$

一个数字比另一个数字多六个。数字之和为二十四。找到数字。

回答: 9、15

练习$\PageIndex{15}$

两个数字的总和为五十八。一个数字比另一个多四。找到数字。

回答: 27、31

练习$\PageIndex{16}$

两个数字的总和为负十四。一个数字比另一个数字小四个。找到数字。

回答

第 1 步。阅读问题。
第 2 步。确定我们在寻找什么。		我们正在寻找两个数字。
第 3 步。姓名。
选择一个变量。		让我们$n=1^{st}$编号。
一个数字比另一个数字少 4。		$n−4=2^{nd}$数字
第 4 步。翻译。
写成一句话。		2 个数字的总和为负 14。
翻译成方程式。		$。$
第 5 步。求解方程。		$。$
将相似的术语组合在一起。		$。$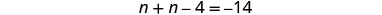
每边加 4 个然后简化。		$。$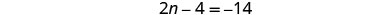
简化。		$。$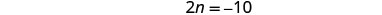
		$。$
		$。$
		$。$
		$。$
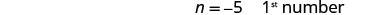
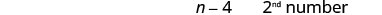
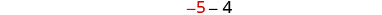
第 6 步。查看。
−9 比 −5 小四吗？	$-5-4\stackrel{?}{=}-9$
	$-9 = -9 \checkmark$
他们的总和是 −14 吗？	$-5+ (-9)\stackrel{?}{=}-14$
	$-14 = -14 \checkmark$
第 7 步。回答问题。		数字是 −5 和 −9。

练习$\PageIndex{17}$

两个数字的总和为负二十三。一个数字比另一个数字少七个。找到数字。

回答: -15、-8

练习$\PageIndex{18}$

两个数字的总和为$−18$。一个数字$40$比另一个多。找到数字。

回答: -29、11

练习$\PageIndex{19}$

一个数字等于十比另一个数字的两倍多。他们的总和是一个。找到数字。

回答

第 1 步。阅读问题。
第 2 步。确定你在找什么。		我们正在寻找两个数字。
第 3 步。姓名。
选择一个变量。		让我们$x=1^{st}$编号。
一个数字是 10 比另一个数字的两倍多。		$2x+10=2^{nd}$数字
第 4 步。翻译。
重述为一句话。		他们的总和是一个。
		这两个数字的总和为 1。
翻译成方程式。		$。$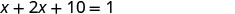
第 5 步。求解方程。
将相似的术语组合在一起。		$。$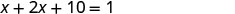
每边减去 10。		$。$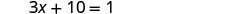
将每边除以 3。		$。$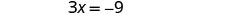
		$。$
		$。$
		$。$
		$。$
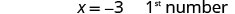
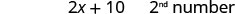
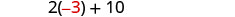
第 6 步。查看。
十大于两倍 −3 等于 4 吗？	$2(-3) + 10 \stackrel{?}{=} 4$
	$-6 + 10 \stacktel{?}{=} 4$
	$4 = 4\checkmark$
他们的总和是1吗？	$-3 + 4 \stackrel{?}{=} 1$
	$1 = 1\checkmark$
第 7 步。回答问题。		数字是 −3 和 −4。

练习$\PageIndex{20}$

一个数字等于八比另一个数字的两倍多。他们的总和是负四。找到数字。

回答: $-4,\; 0$

练习$\PageIndex{21}$

一个数字比另一个数字多三倍。他们的总和是$−5$。找到数字。

回答: $-3,\; -2$

一些数字问题涉及连续的整数。 连续整数是紧随其后的整数。连续整数的示例有：

\[\begin{array}{l}{1,2,3,4} \\ {-10,-9,-8,-7} \\ {150,151,152,153}\end{array}\]

请注意，每个数字都比其前面的数字多一个。因此，如果我们将第一个整数定义为$n$，则下一个连续整数为$n+1$。后面的那个比$n+1$那个多一个$n+1+1$，就是这样$n+2$。
\[\begin{array}{ll}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text { consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

练习$\PageIndex{22}$

两个连续整数的总和为$47$。找到数字。

回答

第 1 步。阅读问题。
第 2 步。确定你在找什么。	两个连续的整数
第 3 步。命名每个数字。	假设$n=1^{st}$为整数。
	$n+1=$下一个连续整数
第 4 步。翻译。
重述为一句话。	整数之和为$47$。
翻译成方程式。	$。$
第 5 步。求解方程。	$。$
将相似的术语组合在一起。	$。$
每边减去 1。	$。$
将每边除以 2。	$。$
	$。$
	$。$
	$。$
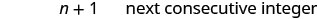
第 6 步。查看。
$\begin{array} {lll} {23 + 24} &{\stackrel{?}{=}} &{47} \\ {47} &{=} &{47\checkmark} \end{array}$
第 7 步。回答问题。	两个连续的整数是 23 和 24。

练习$\PageIndex{23}$

两个连续整数的总和为 95。找到数字。

回答: 47、48

练习$\PageIndex{24}$

两个连续整数的总和为 −31。找到数字。

回答: -16、-15

练习$\PageIndex{25}$

找出总和为 −42 的三个连续整数。

回答

第 1 步。阅读问题。
第 2 步。确定我们在寻找什么。	三个连续的整数
第 3 步。分别命名三个数字。	假设$n=1^{st}$为整数。
	$n+1= 2^{nd}$连续整数
	$n+2= 3^{rd}$连续整数
第 4 步。翻译。
重述为一句话。	三个整数之和为$−42$。
翻译成方程式。	$。$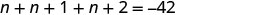
第 5 步。求解方程。	$。$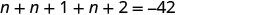
将相似的术语组合在一起。	$。$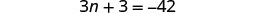
每边减去 3。	$。$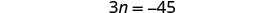
将每边除以 3。	$。$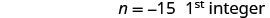
	$。$
	$。$
	$。$
	$。$
	$。$
	$。$
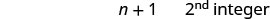
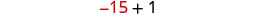
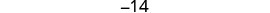
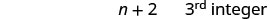
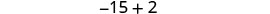
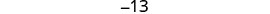
第 6 步。查看。
$\begin{array}{lll} {-13 + (-14) + (-15)} &{\stackrel{?}{=}} &{-42} \\ {-42} &{=} &{-42\checkmark} \end{array}$
第 7 步。回答问题。	三个连续的整数是 −13、−14 和 −15。

练习$\PageIndex{26}$

找出总和为 −96 的三个连续整数。

回答: -33、-32、-31

练习$\PageIndex{27}$

找出总和为 −36 的三个连续整数。

回答: -13、-12、-11

现在我们已经处理了连续的整数，我们将扩展工作范围，将连续的偶数整数和连续的奇数整数包括在内。 连续的偶数整数是紧接着的偶数整数。连续偶数整数的示例有：

\[\begin{array}{l}{18,20,22} \\ {64,66,68} \\ {-12,-10,-8}\end{array}\]

注意每个整数都大$2$于其前面的数字。如果我们调用第一个$n$，那么下一个是$n+2$。下一个是$n+2+2$或$n+4$。
\[\begin{array}{cll}{n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

连续的奇数整数是紧随其后的奇数整数。考虑连续的奇数整数$77$$79$、和$81$。

\[\begin{array}{l}{77,79,81} \\ {n, n+2, n+4}\end{array}\]

\[\begin{array}{cll}{n} & {1^{\text { st }} \text {odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

将2（偶数）相加以从一个奇数到下一个奇数似乎很奇怪吗？当我们将 2 与 3 相加时，你会得到奇数还是偶数？到 11？到 47？

无论问题是要求连续的偶数还是奇数，你都不必做任何不同的事情。模式还是一样的——要从一个奇数或一个偶数到下一个奇数或一个偶数整数，请加 2。

练习$\PageIndex{28}$

找出三个连续的偶数整数，总和为 84。

回答: \[\begin{array}{ll} {\textbf{Step 1. Read} \text{ the problem.}} & {} \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} & {\text{three consecutive even integers}} \\ {\textbf{Step 3. Name} \text{ the integers.}} & {\text{Let } n = 1^{st} \text{ even integers.}} \\ {} &{n + 2 = 2^{nd} \text{ consecutive even integer}} \\ {} &{n + 4 = 3^{rd} \text{ consecutive even integer}} \\ {\textbf{Step 4. Translate.}} &{} \\ {\text{ Restate as one sentence. }} &{\text{The sum of the three even integers is 84.}} \\ {\text{Translate into an equation.}} &{n + n + 2 + n + 4 = 84} \\ {\textbf{Step 5. Solve} \text{ the equation. }} &{} \\ {\text{Combine like terms.}} &{n + n + 2 + n + 4 = 84} \\ {\text{Subtract 6 from each side.}} &{3n + 6 = 84} \\ {\text{Divide each side by 3.}} &{3n = 78} \\ {} &{n = 26 \space 1^{st} \text{ integer}} \\\\ {} &{n + 2\space 2^{nd} \text{ integer}} \\ {} &{26 + 2} \\ {} &{28} \\\\ {} &{n + 4\space 3^{rd} \text{ integer}} \\ {} &{26 + 4} \\ {} &{30} \\ {\textbf{Step 6. Check.}} &{} \\\\ {26 + 28 + 30 \stackrel{?}{=} 84} &{} \\ {84 = 84 \checkmark} & {} \\ {\textbf{Step 7. Answer} \text{ the question.}} &{\text{The three consecutive integers are 26, 28, and 30.}} \end{array}\]

练习$\PageIndex{29}$

找出三个连续的偶数整数，其总和为 102。

回答: 32、34、36

练习$\PageIndex{30}$

找出三个连续的偶数整数，其总和为 −24。

回答: −10、−8、−6

练习$\PageIndex{31}$

一对已婚夫妇每年的总收入为110,000美元。妻子的收入少16,000美元，不到丈夫收入的两倍。丈夫挣多少钱？

回答

第 1 步。阅读问题。
第 2 步。确定我们在寻找什么。	丈夫挣多少钱？
第 3 步。姓名。
选择一个变量来表示丈夫的收入金额。	$h=$把丈夫挣的钱拿出来
妻子的收入还$$16,000$不到这个数额的两倍。	$2h−16,000$妻子的收入金额。
第 4 步。翻译。	夫妻共同赚钱$$110,000$。
用一句话用所有重要信息重述问题。	$。$
翻译成方程式。	$。$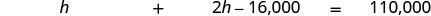
第 5 步。求解方程。	$h + 2h − 16,000 = 110,000$
将相似的术语组合在一起。	$3h − 16,000 = 110,000$
$16,000$在两边都添加并简化。	$3h = 126,000$
将两边除以$3$。	$h = 42,000$
	$$42,000$丈夫的收入金额
	$2h − 16,000$妻子的收入金额
	$2(42,000) − 16,000$
	$84,000 − 16,000$
	$68,000$
第 6 步。查看。
如果妻子赚钱$$68,000$而丈夫的收入$$42,000$是总收入$$110,000$（？是的！
第 7 步。回答问题。	丈夫挣$$42,000$一年。

练习$\PageIndex{32}$

根据全国汽车经销商协会的数据，2014年一辆汽车的平均成本为28,500美元。这比1975年成本低了1,500美元。 1975 年汽车的平均成本是多少？

回答: 5000 美元

练习$\PageIndex{33}$

美国人口普查数据显示，2014年11月美国新房的中位价为280,900美元。这比1964年11月的价格高出10,700美元，比1964年11月的价格高出14倍。 1964 年 11 月新房的中位价是多少？

回答: 19300 美元

关键概念

问题解决策略
1. 阅读问题。确保所有文字和想法都被理解。
2. 确定我们在寻找什么。
3. 说出我们要找的东西。选择一个变量来表示该数量。
4. 翻译成方程式。用一句话用所有重要信息重述问题可能会有所帮助。然后，将英语句子翻译成代数方程。
5. 使用良好的代数技巧求@@ 解方程。
6. 检查问题中的答案并确保答案合理。
7. 用完整的句子@@ 回答问题。
连续整数
连续整数是紧随其后的整数。
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text {consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]

连续的偶数整数是紧接着的偶数整数。
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]

连续的奇数整数是紧随其后的奇数整数。
\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]

	让\(p =\)原价出发。
	\(18\)是原价的一半。
	\(18 = \frac{1}{2}p\)
将两边乘以\(2\)。	\( {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p \)
简化。	\(36 = p\)
查看。钱包的价格合理吗？\($36\)
是的。
\(18\)一半是\(36\)吗？
\(18 \stackrel{?}{=} \frac{1}{2}\cdot 36\)
\(18 = 18\checkmark\)
	钱包的原价是\($36\)。

第 1 步。阅读问题。
第 2 步。确定我们在寻找什么。	丈夫挣多少钱？
第 3 步。姓名。
选择一个变量来表示丈夫的收入金额。	\(h=\)把丈夫挣的钱拿出来
妻子的收入还\($16,000\)不到这个数额的两倍。	\(2h−16,000\)妻子的收入金额。
第 4 步。翻译。	夫妻共同赚钱\($110,000\)。
用一句话用所有重要信息重述问题。	$。$
翻译成方程式。	$。$
第 5 步。求解方程。	\(h + 2h − 16,000 = 110,000\)
将相似的术语组合在一起。	\(3h − 16,000 = 110,000\)
\(16,000\)在两边都添加并简化。	\(3h = 126,000\)
将两边除以\(3\)。	\(h = 42,000\)
	\($42,000\)丈夫的收入金额
	\(2h − 16,000\)妻子的收入金额
	\(2(42,000) − 16,000\)
	\(84,000 − 16,000\)
	\(68,000\)
第 6 步。查看。
如果妻子赚钱\($68,000\)而丈夫的收入\($42,000\)是总收入\($110,000\)（？是的！
第 7 步。回答问题。	丈夫挣\($42,000\)一年。

使用问题解决策略来解决单词问题。

练习\(\PageIndex{1}\)

练习\(\PageIndex{2}\)

练习\(\PageIndex{3}\)

练习\(\PageIndex{4}\)

练习\(\PageIndex{5}\)

练习\(\PageIndex{6}\)

练习\(\PageIndex{7}\)

练习\(\PageIndex{8}\)

练习\(\PageIndex{9}\)

练习\(\PageIndex{10}\)

练习\(\PageIndex{11}\)

练习\(\PageIndex{12}\)

练习\(\PageIndex{13}\)

练习\(\PageIndex{14}\)

练习\(\PageIndex{15}\)

练习\(\PageIndex{16}\)

练习\(\PageIndex{17}\)

练习\(\PageIndex{18}\)

练习\(\PageIndex{19}\)

练习\(\PageIndex{20}\)

练习\(\PageIndex{21}\)

练习\(\PageIndex{22}\)

练习\(\PageIndex{23}\)

练习\(\PageIndex{24}\)

练习\(\PageIndex{25}\)

练习\(\PageIndex{26}\)

练习\(\PageIndex{27}\)

练习\(\PageIndex{28}\)

练习\(\PageIndex{29}\)

练习\(\PageIndex{30}\)

练习\(\PageIndex{31}\)

练习\(\PageIndex{32}\)

练习\(\PageIndex{33}\)

用一句话用所有重要信息重述问题。	\(\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}\)
翻译成方程式。	\(18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p\)