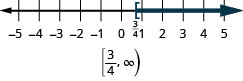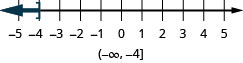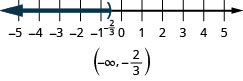2.7: 求解线性不等式
- Page ID
- 204589
在本节结束时,您将能够:
- 在数字线上绘制不等式图
- 使用不等式的减法和加法属性求解不等式
- 使用不等式的除法和乘法属性求解不等式
- 解决需要简化的不等式
- 转化为不等式然后解决
在数字线上绘制不等式图
你还记得一个数字成为方程的解意味着什么吗? 方程的解是一个变量的值,当它被替换到方程中时,该变量的陈述是真实的。
那么不平等的解决方案呢? 什么数字能使不平等成为\(x > 3\)现实? 你在想 “x 可能是 4” 吗? 没错,但是 x 也可能是 5,或者 20,甚至是 3.001。 任何大于 3 的数字都是不等式的解\(x > 3\)。
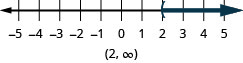
我们通过在 3 右边的所有数字\(x > 3\)上加阴影来显示数字线上不等式的解,以表明所有大于 3 的数字都是解。 因为数字 3 本身不是解,所以我们在 3 处加了一个左括号。 的图表\(x > 3\)如图所示\(\PageIndex{1}\)。 请注意,使用以下惯例:浅蓝色箭头指向正方向,深蓝色箭头指向负方向。
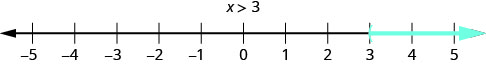
不等式的图\(x \geq 3\)很像的图\(x > 3\),但现在我们需要证明3也是一个解。 我们通过在方括号处加上方括号来做到这一点\(x = 3\),如图所示\(\PageIndex{2}\)。
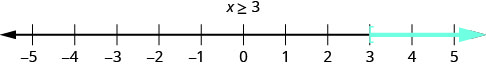
请注意,左括号符号 (,表示不等式的端点不包括在内。 开括号符号 [表示包含端点。
数字行上的图表:
- \(x\leq 1\)
- \(x<5\)
- \(x>−1\)
- 回答
-
1。 \(x\leq 1\)这意味着所有数字小于或等于 1。 我们用 1 左边的数字行上的所有数字加上阴影,然后在 x=1 处加上方括号以表明它包含在内。
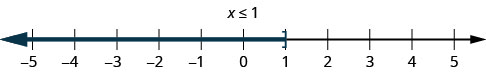
2。 \(x<5\)这意味着所有数字都小于 5,但不包括 5。 我们用 5 左边的数字行上的所有数字加上阴影,然后在 x=5 处加上圆括号,表示它不包括在内。
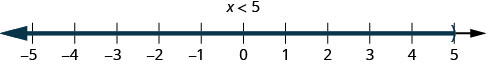
3。 \(x>−1\)这意味着所有大于 −1 的数字,但不包括 −1。 我们用 −1 右边的数字行上的所有数字加上阴影,然后在 x=−1 处加上圆括号,表示它不包括在内。
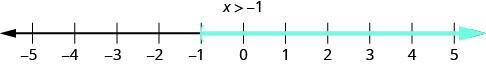
数字行上的图表:
- \(x\leq −1\)
- \(x>2\)
- \(x<3\)
- 回答
-
数字行上的图表:
- \(x>−2\)
- \(x<−3\)
- \(x\geq −1\)
- 回答
-
我们也可以使用区间表示法来表示不等式。 正如我们在上面看到的,不等\(x>3\)式意味着所有大于 3 的数字。 这种不平等的解决方案没有上限。 在间隔表示法中,我们表示\(x>3\)为\((3, \infty)\)。 该符号被读\(\infty\)为 “无限”。 这不是一个实际的数字。 图中同时\(\PageIndex{3}\)显示了数字线和间隔符号。

不等\(x\leq 1\)式表示所有小于或等于 1 的数字。 这些数字没有下限。 我们用间隔表示法写\(x\leq 1\)成\((-\infty, 1]\)。 该符号\(-\infty\)被读为 “负无穷大”。 图中同时\(\PageIndex{4}\)显示了数字行和间隔符号。


你注意到间隔符号中的括号或方括号与箭头端点的符号如何匹配吗? 这些关系如图所示\(\PageIndex{5}\)。

在数字行上绘制图形并用间隔符号书写。
- \(x \geq -3\)
- \(x<2.5\)
- \(x\leq \frac{3}{5}\)
- 回答
-
1。
2。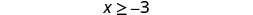
在 −3 的右侧加上阴影,并在 −3 处加上方括号。 
用间隔符号书写。 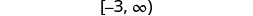
3。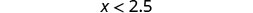
在 2.5 的左边加上阴影,然后在 2.5 处加上一个括号。 
用间隔符号书写。 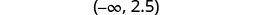
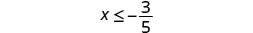
将阴影移到左边\(-\frac{3}{5}\),然后在上面放一个括号\(-\frac{3}{5}\)。 
用间隔符号书写。 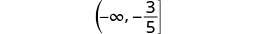
在数字行上绘制图形并用间隔符号书写:
- \(x>2\)
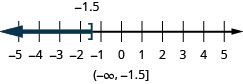
- \(x\leq −1.5\)
- \(x\geq \frac{3}{4}\)
- 回答
-
在数字行上绘制图形并用间隔符号书写:
- \(x\leq −4\)
- \(x\geq 0.5\)
- \(x<-\frac{2}{3}\)
- 回答
-
使用不等式的减法和加法属性求解不等式
相等的减法和加法属性指出,如果两个量相等,当我们从两个量中相加或减去相同的数量时,结果将相等。
\[\begin{array} { l l } { \textbf { Subtraction Property of Equality } } & { \textbf { Addition Property of Equality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if } \qquad \quad a = b , } & { \text { if } \qquad \quad a = b } \\ { \text { then } a - c = b - c . } & { \text { then } a + c = b + c } \end{array}\]
对于不等式,类似的属性也适用。
| 例如,我们知道 −4 小于 2。 | 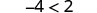 |
| 如果我们从两个数量中减去 5,左边还小于右边吗? | 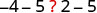 |
| 我们在左边得到 −9,右边得到 −3。 |  |
| 而且我们知道 −9 小于 −3。 |  |
|
不平等的迹象保持不变。 |
同样,我们可以证明加法的不等式也保持不变。
这使我们想到了不等式的减法和加法属性。
\[\begin{array} { l l } { \textbf { Subtraction Property of Inequality } } & { \textbf { Addition Property of Inequality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if }\qquad \quad a < b } & { \text { if } \qquad \quad a < b } \\ { \text { then } a - c < b - c . } & { \text { then } a + c < b + c } \\\\ { \text { if } \qquad \quad a > b } & { \text { if } \qquad \quad a > b } \\ { \text { then } a - c > b - c . } & { \text { then } a + c > b + c } \end{array}\]
我们使用这些属性来求解不等式,所采用的步骤与求解方程的步骤相同。 解决不平等问题\(x+5>9\),步骤将如下所示:
\[\begin{array}{rrll} {} &{x + 5} &{ >} &{9} \\ {\text{Subtract 5 from both sides to isolate }x.} &{x + 5 - 5} &{ >} &{9 - 5} \\{} &{x} &{ >} &{4} \\ \end{array}\]
任何大于 4 的数字都是这种不等式的解法。
求解不\(n - \frac{1}{2} \leq \frac{5}{8}\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
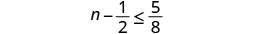
再\(\frac{1}{2}\)加上不平等的两面。 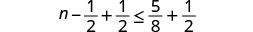
简化。 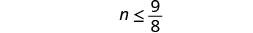
在数字行上绘制解法。 
用间隔表示法写出解。
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(p - \frac{3}{4} \geq \frac{1}{6}\)
- 回答
-
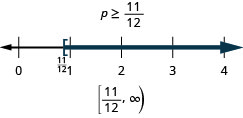
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(r - \frac{1}{3} \leq \frac{7}{12}\)
- 回答
-
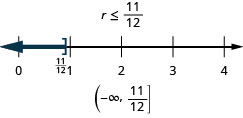
使用不等式的除法和乘法属性求解不等式
相等的除法和乘法属性指出,如果两个量相等,当我们将两个量除以或乘以相同的量时,结果也将相等(前提是我们不除以 0)。
\[\begin{array}{ll} {\textbf{Division Property of Equality}} &{\textbf{MUltiplication Property of Equality}} \\ {\text{For any numbers a, b, c, and c} \neq 0} &{\text{For any numbers a, b, c}} \\ {\text{if } \qquad a = b} &{\text{if} \qquad \quad a = b} \\ {\text{then }\quad \frac{a}{c} = \frac{b}{c}} &{\text{then } \quad ac = bc} \end{array}\]
不等式有类似的特性吗? 当我们将两边除以或乘以一个常数时,不等式会发生什么?
考虑一些数字示例。
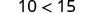 |
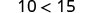 |
||
| 将两边除以 5。 | 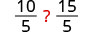 |
将两边乘以 5。 |  |
| 简化。 |  |
 |
|
| 填写不等式标志。 |  |
 |
不平等迹象保持不变。
当我们除以或乘以负数时,不等式是否保持不变?
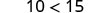 |
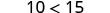 |
||
| 将两边除以 -5。 | 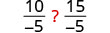 |
将两边乘以 -5。 |  |
| 简化。 |  |
 |
|
| 填写不等式标志。 |  |
 |
不平等的迹象扭转了方向。
当我们将不等式除以或乘以正数时,不等式符号保持不变。 当我们将不等式除以或乘以负数时,不等式符号反转。
以下是不等式的除法和乘法属性,便于参考。
对于任何实数 a、b、c
\[\begin{array}{ll} {\text{if } a < b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \\ {\text{if } a > b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a < b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a > b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \end{array}\]
当我们将不等式除以或乘以 a 时:
- 正数,不等式保持不变。
- 负数,不等式反转。
求解不\(7y<42\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
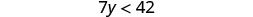
将不等式的两边除以 7。
因为\(7>0\),不等式保持不变。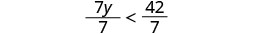
简化。 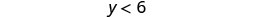
在数字行上绘制解法。 
用间隔表示法写出解。 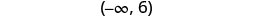
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(9c>72\)
- 回答
-
\(c>8\)

\((8, \infty)\)
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(12d\leq 60\)
- 回答
-
\(d\leq 5\)

\((-\infty, 5]\)
求解不\(−10a\geq 50\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
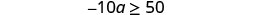
将不等式的两边除以 −10。
从那以后\(−10<0\),这种不平等性发生了逆转。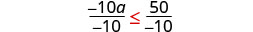
简化。 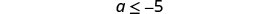
在数字行上绘制解法。 
用间隔表示法写出解。 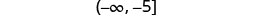
求解每个不等式,在数字线上绘出解,然后用区间表示法写出解。
\(−8q<32\)
- 回答
-
\(q>−4\)
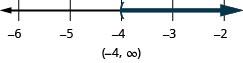
求解每个不等式,在数字线上绘出解,然后用区间表示法写出解。
\(−7r\leq −70\)
- 回答
-
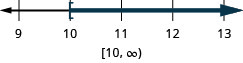
有时,在求解不等式时,变量最终会出现在右边。 我们可以反向重写不等式,将变量放在左边。
\[\begin{array}{l} x > a\text{ has the same meaning as } a < x \end{array}\]
可以把它当作 “如果泽维尔比亚历克斯高,那么亚历克斯比泽维尔短。”
求解不\(-20 < \frac{4}{5}u\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
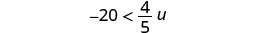
将不等式的两边乘以\(\frac{5}{4}\)。
因为\(\frac{5}{4} > 0\),不等式保持不变。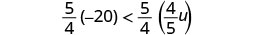
简化。 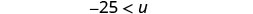
重写左边的变量。 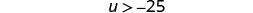
在数字行上绘制解法。 
用间隔表示法写出解。 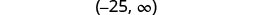
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(24 \leq \frac{3}{8}m\)
- 回答
-
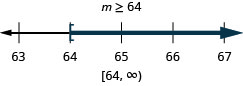
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(-24 < \frac{4}{3}n\)
- 回答
-
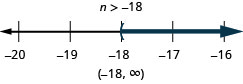
求解不\(\frac{t}{-2} \geq 8\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
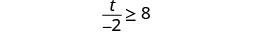
将不等式的两边乘以 −2。
从那以后\(−2<0\),这种不平等性发生了逆转。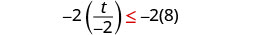
简化。 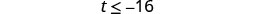
在数字行上绘制解法。 
用间隔表示法写出解。 
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(\frac{k}{-12}\leq 15\)
- 回答
-
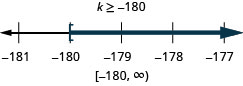
求解不等式,在数字线上绘出解,然后用区间表示法写出解。
\(\frac{u}{-4}\geq -16\)
- 回答
-
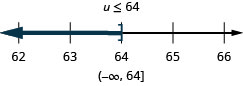
解决需要简化的不等式
大多数不平等需要不止一个步骤才能解决。 我们遵循与求解线性方程的通用策略相同的步骤,但是在乘法或除法时一定要密切注意。
求解不\(4m\leq 9m+17\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
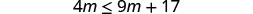
从两边减去 9m 以收集左边的变量。 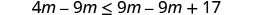
简化。 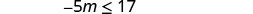
将不等式的两边除以 −5,然后反转不等式。 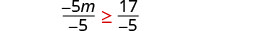
简化。 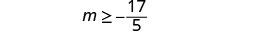
在数字行上绘制解法。 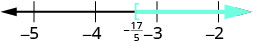
用间隔表示法写出解。 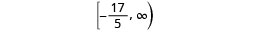
求解不\(3q\geq 7q−23\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
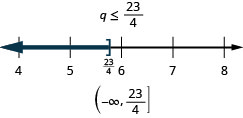
求解不\(6x<10x+19\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
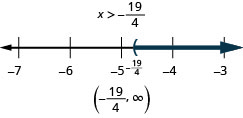
求解不等式\(8p+3(p−12)>7p−28\)图解在数字线上绘制解,然后用区间表示法写出解。
- 回答
-
尽可能简化每一面。 8p+3 (p−12) >7p−28 分发。 8p+3p−36>7p−28 将相似的术语组合在一起。 11p−36>7p−28 从两边减去 7p 以收集左边的变量。 11p−36−7p>7p−28−7p 简化。 4p−36>−28 在两边加上 36 以收集右边的常量。 4p−36+36>−28+36 简化。 4p>8 将不等式的两边除以 4;不等式保持不变。 \(\frac{4p}{4}>84\) 简化。 \(p>2\) 在数字行上绘制解法。 
用间隔表示法写出解。 \((2, \infty)\)
求解不\(9y+2(y+6)>5y−24\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
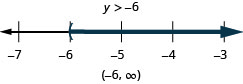
求解不\(6u+8(u−1)>10u+32\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
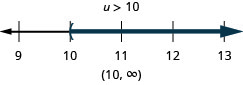
就像有些方程是身份而有些是矛盾一样,不平等也可能是身份或矛盾。 当我们在解决不等式时只剩下常量时,我们就会认出这些形式。 如果结果是真实的陈述,那么我们就有了身份。 如果结果是虚假陈述,那么我们就有矛盾了。
求解不\(8x−2(5−x)<4(x+9)+6x\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
尽可能简化每一面。 8x−2 (5−x) <4 (x+9) +6x 分发。 8x−10+2x<4x+36+6x 将相似的术语组合在一起。 10x−10<10x+36 从两边减去 10 倍以收集左边的变量。 10x−10−10x<10x+36−10x 简化。 −10<36 xx 不见了,我们有了一个真实的陈述。 不平等是一种身份。
解决方案都是实数。在数字行上绘制解法。 
用间隔表示法写出解。 \((-\infty, \infty)\)
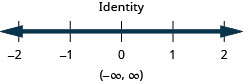
求解不\(4b−3(3−b)>5(b−6)+2b\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
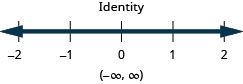
求解不\(9h−7(2−h)<8(h+11)+8h\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
求解不\(\frac{1}{3}a - \frac{1}{8}a > \frac{5}{24}a + \frac{3}{4}\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
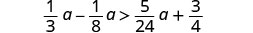
将两边乘以液晶屏 24 以清除分数。 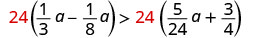
简化。 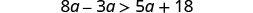
将相似的术语组合在一起。 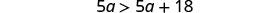
从两边减去 5a 以收集左边的变量。 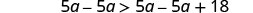
简化。 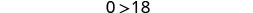
这个说法是错误的! 不平等是矛盾的。 没有解决办法。 在数字行上绘制解法。 
用间隔表示法写出解。 没有解决办法。
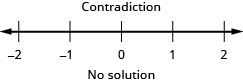
求解不\(\frac{1}{4}x - \frac{1}{12}x > \frac{1}{6}x + \frac{7}{8}\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
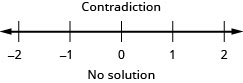
求解不\(\frac{2}{5}z - \frac{1}{3}z < \frac{1}{15}z - \frac{3}{5}\)等式,在数字线上绘出解,然后用区间表示法写出解。
- 回答
-
转化为不等式并求解
要将英语句子翻译成不等式,我们需要识别表示不平等的短语。 有些词很简单,比如 “大于” 和 “小于”。 但是其他的并不那么明显。
想想 “至少” 这个词—— “至少 21 岁” 是什么意思? 这意味着 21 或更多。 短语 “至少” 与 “大于或等于” 相同。
该表\(\PageIndex{4}\)[1]显示了一些表示不平等的常用短语。
| > | \(\geq\) | < | \(\leq\) |
|---|---|---|---|
| “data-valign= “middle” class= “lt-math-15134” > 大于 | \ (\ geq\)” data-valign= “middle” class= “lt-math-15134” > 大于或等于 | 小于 | \ (\ leq\)” data-valign= “middle” class= “lt-math-15134” > 小于或等于 |
| “data-valign= “middle” class= “lt-math-15134” > 超过 | \ (\ geq\)” data-valign= “middle” class= “lt-math-15134” > 至少是 | 小于 | \ (\ leq\)” data-valign= “middle” class= “lt-math-15134” > 最多是 |
| “data-valign= “middle” class= “lt-math-15134” > 大于 | \ (\ geq\)” data-valign= “middle” class= “lt-math-15134” > 不少于 | 少于 | \ (\ leq\)” data-valign= “middle” class= “lt-math-15134” > 不超过 |
| “data-valign= “middle” class= “lt-math-15134” > 超过 | \ (\ geq\)” data-valign= “middle” class= “lt-math-15134” > 是最小值 | 低于 | \ (\ leq\)” data-valign= “middle” class= “lt-math-15134” > 是最大值 |
翻译并解决。 然后用区间表示法在数字行上写下解和图形。
十二倍 c 不超过 96。
- 回答
-
翻译。 
求解-将两边除以 12。 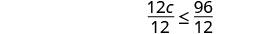
简化。 
用间隔符号书写。 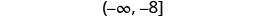
数字线上的图形。 
翻译并解决。 然后用区间表示法在数字行上写下解和图形。
二十倍 y 最多为 100
- 回答
-
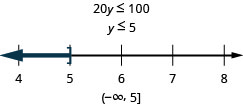
翻译并解决。 然后用区间表示法在数字行上写下解和图形。
九倍 z 不小于 135
- 回答
-
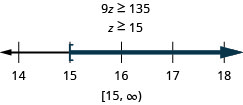
翻译并解决。 然后用区间表示法在数字行上写下解和图形。
比 x 小三十至少等于 45。
- 回答
-
翻译。 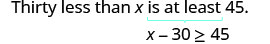
求解-两边加 30。 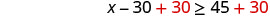
简化。 
用间隔符号书写。 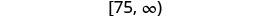
数字线上的图形。 
翻译并解决。 然后用区间表示法在数字行上写下解和图形。
小于 p 的十九不小于 47
- 回答
-
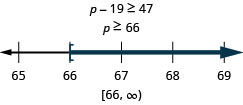
翻译并解决。 然后用区间表示法在数字行上写下解和图形。
比 a 多四个最多为 15。
- 回答
-
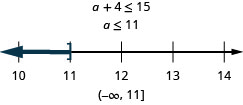
关键概念
- 不等式的减法属性
对于任何数字 a、b 和 c,
如果 a<b 然后是 a−c<b−c;
如果 a>b 则是 a−c>b−c。 - 不等式@@ 的加法属性
对于任何数字 a、b 和 c,
如果 a<b 然后是 a+c<b+c;
如果 a>b 则是 a+c>b+c。 - 不等式 y 的除法和乘法属性
对于任何数字 a、b 和 c,
如果 a <b and c>0,则为 ac <bc and ac>bc。
如果 a>b 和 c>0,那么 ac>bc 和 ac>bc。
如果 a<b 和 cbc<0, then ac> 和 ac>bc。
如果 a>b 和 c<0,那么 ac<bc 和 ac<bc。 - 当我们将不等式除以或乘以 a 时:
- 正数,不等式保持不变。
- 负数,不等式反转。