2.6:求解特定变量的公式
- Page ID
- 204590
在本节结束时,您将能够:
- 使用距离、速率和时间公式
- 求解特定变量的公式
使用距离、速率和时间公式
你在代数和日常生活中经常使用的一个公式是物体以恒定速度移动的距离的公式。 速率是 “速度” 的等效词。 你可能已经熟悉了费率的基本概念。 你知道如果你以每小时 60 英里的稳定速度行驶 2 小时,你会行驶多远吗? (如果你在高速公路上行驶时使用汽车的巡航控制系统,可能会发生这种情况。) 如果你说 120 英里,你已经知道如何使用这个公式了!
对于以统一(恒定)速率移动的物体,行进距离、经过的时间和速率通过以下公式相互关联:
\[\begin{array} {lllll}{ d = r t} &{\text { where }} &{ d} &{=} &{\text{distance}} \\ {} &{} &{ r} &{=} &{\text{rate}} \\{} &{} &{ t} &{=} &{\text{time}} \end{array}\]
我们将使用本章前面使用的 “求解应用程序的策略”。 当我们的问题需要公式时,我们会更改步骤 4。 我们不用写句子,而是写出相应的公式。 我们在此处写下修订后的步骤以供参考。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 针对情况写出相应的公式。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
你可能需要创建一个小图表来总结问题中的信息。 参见第一个示例中的图表。
贾马尔以每小时 12 英里的统一速度骑自行车,持续\(3\frac{1}{2}\)数小时。 他走了多远?
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 行进距离 第 3 步。 姓名。 选择一个变量来表示它。 假设 d = 距离。 第 4 步。 翻译:写出相应的公式。 \(d=rt\) 
在给定的信息中替换。 \(d = 12\cdot 3\frac{1}{2}\) 第 5 步。 求解方程。 \(d=42\text{ miles}\) 第 6 步。 查看 42 英里有意义吗? 贾马尔骑行: 
第 7 步。 用完整的句子回答问题。 贾马尔骑了 42 英里。
林赛以每\(5\frac{1}{2}\)小时 60 英里的速度开了好几个小时。 她走了多少距离?
- 回答
-
330 英里
Trinh 以每\(2\frac{1}{3}\)小时 3 英里的速度走了好几个小时。 她走了多远?
- 回答
-
7 英里
雷伊正计划从他在圣地亚哥的家中开车去萨克拉曼多探望祖母,距离520英里。 如果他能以每小时 65 英里的稳定速度行驶,那么这次旅行需要多少小时?
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定你在找什么。 多少小时(时间) 第 3 步。 姓名。
选择一个变量来表示它。让 t = 时间。 
第 4 步。 翻译。
写出相应的公式。\(d=rt\) 在给定的信息中替换。 \(520 = 65t\) 第 5 步。 求解方程。 \(t = 8\) 第 6 步。 查看。 将数字代入公式
中,并确保结果是
真实的陈述。\(\begin{array}{lll} {d} &{=} &{rt} \\ {520} &{\stackrel{?}{=}} &{65\cdot 8}\\ {520} &{=} &{520\checkmark} \end{array}\) 第 7 步。 用完整的句子回答问题。 雷伊的旅行需要 8 个小时。
李想从凤凰城开车到他兄弟在旧金山的公寓,距离770英里。 如果他以每小时 70 英里的稳定速度行驶,那么这次旅行需要多少小时?
- 回答
-
11 个小时
叶塞尼亚距离芝加哥 168 英里。 如果她需要在 3 小时内到达芝加哥,她需要以什么速度开车?
- 回答
-
56 mph
求解特定变量的公式
你可能熟悉一些几何公式。 公式是对变量之间关系的数学描述。 公式也用于科学,例如化学、物理和生物学。 在医学中,它们用于计算配药或确定体重指数。 电子表格程序依靠公式进行计算。 熟悉公式并能够轻松操作它们很重要。
在 “运动\(\PageIndex{1}\)与运动” 中\(\PageIndex{4}\),我们使用了公式\(d=rt\)。 这个公式给出 d 的值,即距离,当你用 r 和 t 的值代替时,速率和时间。 但是在练习中\(\PageIndex{4}\),我们必须找到 t 的值。我们用 d 和 r 的值代替,然后用代数求解 tt。 如果你必须经常这样做,你可能会想知道,当你替换 d 和 r 的值时,为什么没有一个公式可以给出 t 的值。我们可以通过求解 t 的公式来得\(d=rt\)出这样的公式。
求解特定变量的公式意味着将该变量隔离在等号的一侧,系数为 1。 所有其他变量和常量都在等号的另一边。 要了解如何求解特定变量的公式,我们将从距离、速率和时间公式开始。
求解 t 的公式 d=rt:
- 当 d=520 和 r=65 时
- 一般来说
- 回答
-
我们将并排编写解法,以证明求解公式通常使用与有数字要替换时的步骤相同。
1. 当 d=520 和 r=65 时 2. 一般来说 写下公式。 \(d=rt\) 写下公式。 \(d=rt\) 替代。 \(520=65t\) 分开,隔离 t。 \(\frac{520}{65} = \frac{65t}{65}\) 分开,隔离 tt。 \(\frac{d}{r} = \frac{rt}{t}\) 简化。 \(8 = t\) 简化。 \(\frac{d}{r}=t\) 我们说公式\(t = \frac{d}{r}\)为 t 求解了。
求解 r\(d=rt\) 的公式:
- 当 d=180 和 t=4 时
- 一般来说
- 回答
-
- \(r = 45\)
- \(r = \frac{d}{t}\)
求解 r\(d=rt\) 的公式:
- 当 d=780 和 t=12 时
- 一般来说
- 回答
-
- \(r = 65\)
- \(r = \frac{d}{rt\)
求解 h\(A = \frac{1}{2}bh\) 的公式:
- 何时\(A = 90\)和\(b = 15\)
- 一般来说
- 回答
-
如果我们知道面积和底部,我们现在可以使用公式找到三角形的高度\(h = \frac{2A}{b}\)1. 何时\(A = 90\)和\(b = 15\) 2. 一般来说 写下公式。 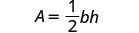
写下公式。 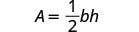
替代。 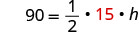
清除分数。 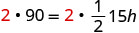
清除分数。 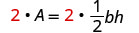
简化。 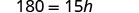
简化。 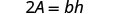
求解 h。 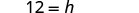
求解 hh。 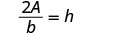
求解 h\(A = \frac{1}{2}bh\) 的公式:
- 何时\(A = 170\)和\(b = 17\)
- 一般来说
- 回答
-
- \(h = 20\)
- \(h = \frac{2A}{b}\)
求解 h\(A = \frac{1}{2}bh\) 的公式:
- 何时\(A = 62\)和\(h = 31\)
- 一般来说
- 回答
-
- \(b = 4\)
- \(b = \frac{2A}{h}\)
该公式\(I=Prt\)用于计算按利率 r 投资的本金 P 的单息 I,持续 t 年。
求解公式 I=Prt 以求出本数 P:
- 当我 = 5,600 美元,r= 4%,t=7 年时
- 一般来说
- 回答
-
1。 I=5,600 美元,r= 4%,t=7 年 2. 一般来说 写下公式。 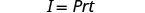
写下公式。 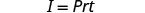
替代。 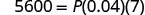
简化。 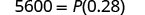
简化。 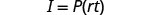
除以,隔离 P。 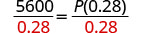
除以,隔离 P。 
简化。 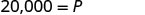
简化。 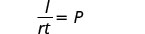
校长是 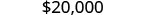
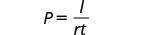
求解公式 I=Prt 以求出本数 P:
- 当我 = 2160 美元时,r= 6%,t=3 年
- 一般来说
- 回答
-
- 12000 美元
- \(P = \frac{1}{rt}\)
求解公式 I=Prt 以求出本数 P:
- 当我 = 5400 美元时,r= 12%,t=5 年
- 一般来说
- 回答
-
- 9000 美元
- \(P = \frac{1}{rt}\)
求解 y 的公式 3x+2y=18:
- 当 x=4 时
- 一般来说
- 回答
-
1. 当 x=4 时 2. 一般来说 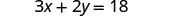
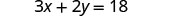
替代。 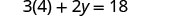
减去可分离
y 项。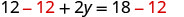
减去可分离
y 项。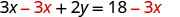
除以。 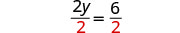
除以。 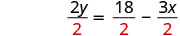
简化。 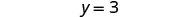
简化。 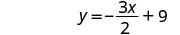
求解 y 的公式 3x+4y=10:
- 什么时候\(x = \frac{14}{3}\)
- 一般来说
- 回答
-
- \(y = -1\)
- \(y = \frac{10 - 3x}{4}\)
求解 y 的公式 5x+2y=18:
- 什么时候\(x = 4\)
- 一般来说
- 回答
-
- \(y = -1\)
- \(y = \frac{18 - 5x}{2}\)
求解 a 的公式 p=a+b+c。
- 回答
-
我们将在方程的一侧隔离 aa。 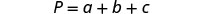
b 和 c 都被加到 a 中,因此我们从方程的两边减去它们。 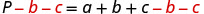
简化。 
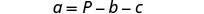
求解 b 的公式 p=a+b+c。
- 回答
-
b=p−a−c
求解 c 的公式 p=a+b+ c。
- 回答
-
c=p−a−b
求解 y 的公式 6x+5y=13。
- 回答
-
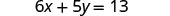
从两边减去 6 倍以将该项与 y 隔离。 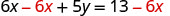
简化。 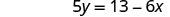
除以 5 得出系数 1。 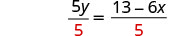
简化。 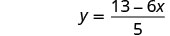
分数已简化。 我们不能将 13−6x 除以 5。
求解 y 的公式 4x+7y=9。
- 回答
-
\(y = \frac{9 - 4x}{7}\)
求解 y 的公式 5x+8y=1。
- 回答
-
\(y = \frac{1 - 5x}{8}\)
关键概念
- 求解应用程序(使用公式)
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 针对情况写出相应的公式。 在给定的信息中替换。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
- 距离、速率和时间
对于以统一(恒定)速率移动的物体,行进距离、经过的时间和速率由以下公式相关:d=rt 其中 d = 距离,r = 速率,t = 时间。 - 求解特定变量的公式意味着单独获得该变量,方程一侧的系数为 1,另一侧为所有其他变量和常量。


