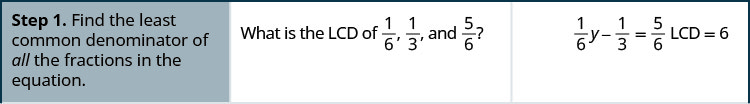2.5:用分数或小数求解方程
- Page ID
- 204693
在本节结束时,您将能够:
- 使用分数系数求解方程
- 使用十进制系数求解方程
使用分数系数求解方程
让我们使用前面介绍的求解线性方程的通用策略来求解方程\(\frac{1}{8}x+\frac{1}{2}=\frac{1}{4}\)。
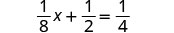 |
|
| 要分离 x 项,请\(\frac{1}{2}\)从两边减去。 | 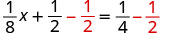 |
| 简化左侧。 | 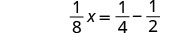 |
| 使用液晶屏将常数更改为等效分数。 | 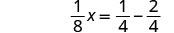 |
| 减去。 |  |
| 将两边乘以的倒数\(\frac{1}{8}\)。 |  |
| 简化。 | 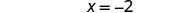 |
这种方法效果很好,但是许多学生在看到所有这些分数时并不感到非常自信。 因此,我们将展示一种用分数求解方程的另一种方法。 这种替代方法消除了分数。
我们将应用相等的乘法属性,将方程的两边乘以方程中所有分数的最小公分母。 此运算的结果将是一个新方程,等同于第一个方程,但没有分数。 这个过程被称为 “清除” 分数方程。
让我们求解一个类似的方程,但这次使用消除分数的方法。
解决:\(\frac{1}{6}y - \frac{1}{3} = \frac{5}{6}\)
回答
解决:\(\frac{1}{4}x + \frac{1}{2} = \frac{5}{8}\)
- 回答
-
\(x= \frac{1}{2}\)
解决:\(\frac{1}{8}x + \frac{1}{2} = \frac{1}{4}\)
- 回答
-
\(x = -2\)
请注意,在练习中\(\PageIndex{1}\),一旦我们清除了分数方程,该方程就像我们在本章前面求解的方程一样。 我们把问题改成了我们已经知道如何解决的问题! 然后,我们使用了求解线性方程的通用策略。
- 找出方程中所有分数的最小公分母。
- 将方程的两边乘以该液晶屏。 这会清除分数。
- 使用求解线性方程的通用策略进行求解。
解决:\(6 = \frac{1}{2}v + \frac{2}{5}v - \frac{3}{4}v\)
- 回答
-
我们想通过将方程的两边乘以方程中所有分数的液晶显示屏来清除分数。
找到方程中所有分数的 LCD。 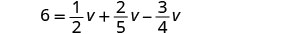
液晶屏是 20。 将方程的两边乘以 20。 
分发。 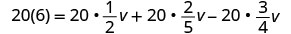
Simplify——注意,别再分数了! 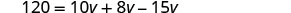
将相似的术语组合在一起。 
除以 3。 
简化。 
查看: 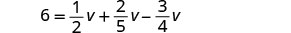
让 v=40。 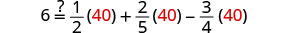
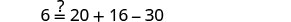

解决:\(7 = \frac{1}{2}x + \frac{3}{4}x - \frac{2}{3}x\)
- 回答
-
\(x = 12\)
解决:\(-1 = \frac{1}{2}u + \frac{1}{4}u - \frac{2}{3}u\)
- 回答
-
\(u = -12\)
在下一个示例中,我们再次在方程的两边都有变量。
解决:\(a + \frac{3}{4} = \frac{3}{8}a - \frac{1}{2}\)
- 回答
-
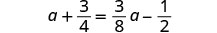
找到方程中所有分数的 LCD。
液晶屏为 8。将两边乘以液晶屏。 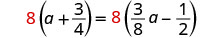
分发。 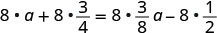
简化-不再有分数。 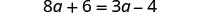
从两边减去 3a3a。 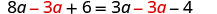
简化。 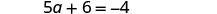
从两边减去 6。 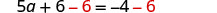
简化。 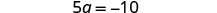
除以 5。 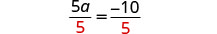
简化。 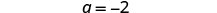
查看: 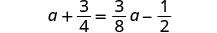
让 a=−2。 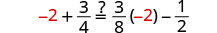
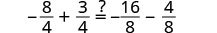
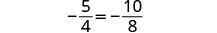
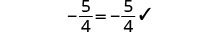
解决:\(x + \frac{1}{3} = \frac{1}{6}x - \frac{1}{2}\)
- 回答
-
\(x = -1\)
解决:\(c + \frac{3}{4} = \frac{1}{2}c - \frac{1}{4}\)
- 回答
-
\(c = -2\)
在下一个示例中,我们首先使用分布属性。 此步骤会立即清除分数。
解决:\(-5 = \frac{1}{4}(8x + 4)\)
- 回答
-
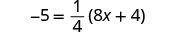
分发。 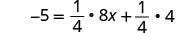
简化。
现在没有分数了。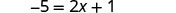
从两边减去 1。 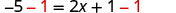
简化。 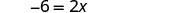
除以 2。 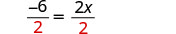
简化。 
查看: 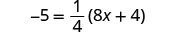
让 x=−3。 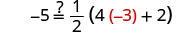
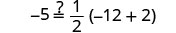
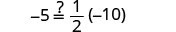
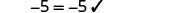
解决:\(-11 = \frac{1}{2}(6p + 2)\)
- 回答
-
\(p = -4\)
解决:\(8 = \frac{1}{3}(9q + 6)\)
- 回答
-
\(q = 2\)
在下一个例子中,即使在分布之后,我们仍有分数需要清除。
解决:\(\frac{1}{2}(y - 5) = \frac{1}{4}(y - 1)\)
- 回答
-
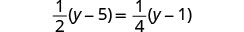
分发。 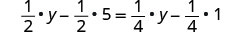
简化。 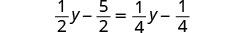
乘以液晶屏,4。 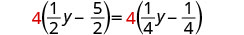
分发。 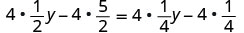
简化。 
收集左边的变量。 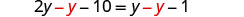
简化。 
收集右边的常量。 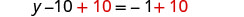
简化。 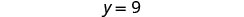
查看: 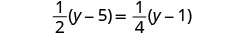
让 y=9。 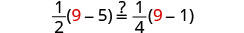
自己完成支票。
解决:\(\frac{1}{5}(n + 3) = \frac{1}{4}(n + 2)\)
- 回答
-
\(n = 2\)
解决:\(\frac{1}{2}(m - 3) = \frac{1}{4}(m - 7)\)
- 回答
-
\(m = -1\)
解决:\(\frac{5x - 3}{4} = \frac{x}{2}\)
- 回答
-
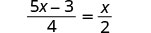
乘以液晶屏,4。 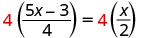
简化。 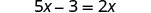
收集右边的变量。 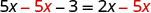
简化。 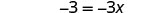
除以。 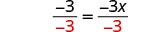
简化。 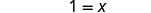
查看: 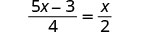
让 x=1。 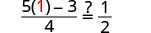
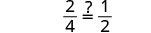
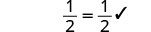
解决:\(\frac{4y - 7}{3} = \frac{y}{6}\)
- 回答
-
\(y = 2\)
解决:\(\frac{-2z - 5}{4} = \frac{z}{8}\)
- 回答
-
\(z = -2\)
解决:\(\frac{a}{6} + 2 = \frac{a}{4} + 3\)
- 回答
-
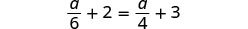
乘以液晶屏 12。 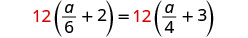
分发。 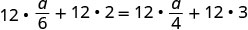
简化。 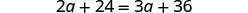
收集右边的变量。 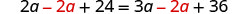
简化。 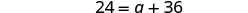
收集左边的常量。 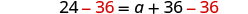
简化。 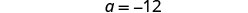
查看: 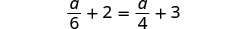
让 a=−12。 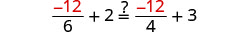
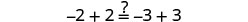
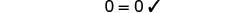
解决:\(\frac{b}{10} + 2 = \frac{b}{4} + 5\)
- 回答
-
\(b = -20\)
解决:\(\frac{c}{6} + 3 = \frac{c}{3} + 4\)
- 回答
-
\(c= -6\)
解决:\(\frac{4q + 3}{2}+ 6 = \frac{3q + 5}{4}\)
- 回答
-
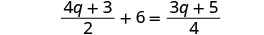
乘以液晶屏,4。 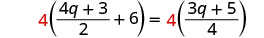
分发。 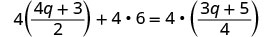
简化。 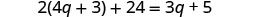
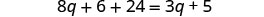
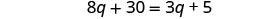
收集左边的变量。 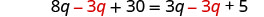
简化。 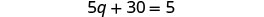
收集右边的常量。 
简化。 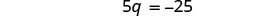
除以 5。 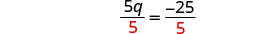
简化。 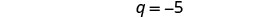
查看: 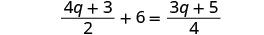
让 q=−5。 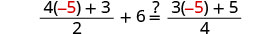
自己完成支票。
解决:\(\frac{3r + 5}{6}+ 1 = \frac{4r + 3}{3}\)
- 回答
-
\(r = 1\)
解决:\(\frac{2s + 3}{2}+ 1 = \frac{3s + 2}{4}\)
- 回答
-
\(s = -8\)
使用十进制系数求解方程
有些方程中有小数。 当我们解决处理金钱或百分比的问题时,就会出现这种方程式。 但是小数也可以表示为分数。 例如,\(0.3 = \frac{3}{10}\)和\(0.17 = \frac{17}{100}\)。 因此,对于带小数的方程,我们可以使用与清除分数相同的方法——将方程的两边乘以最小公分母。
解决:\(0.06x + 0.02 = 0.25x - 1.5\)
- 回答
-
看看小数,想想等效的分数。
\(0.06 = \frac { 6 } { 100 } \quad 0.02 = \frac { 2 } { 100 } \quad 0.25 = \frac { 25 } { 100 } \quad 1.5 = 1 \frac { 5 } { 10 }\)
注意,液晶屏为 100。
通过乘以液晶屏,我们将清除方程中的小数。
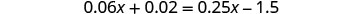
将两边乘以 100。 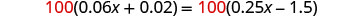
分发。 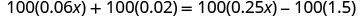
乘以,现在我们没有小数了。 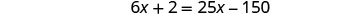
收集右边的变量。 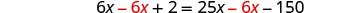
简化。 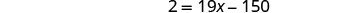
收集右边的变量。 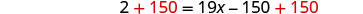
简化。 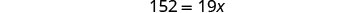
除以 19。 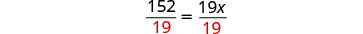
简化。 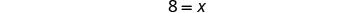
查看:让 x=8
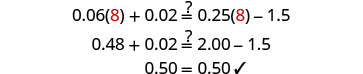
解决:\(0.14h + 0.12 = 0.35h - 2.4\)
- 回答
-
\(h = 12\)
解决:\(0.65k - 0.1 = 0.4k - 0.35\)
- 回答
-
\(k = -1\)
下一个示例使用了下一章中货币应用的典型方程式。 请注意,我们在清除所有小数点之前先分配小数。
解决:\(0.25x + 0.05(x + 3) = 2.85\)
- 回答
-
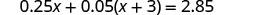
先分发。 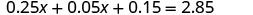
将相似的术语组合在一起。 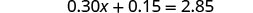
要清除小数,请乘以 100。 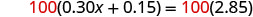
分发。 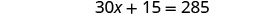
从两边减去 15。 
简化。 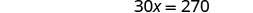
除以 30。 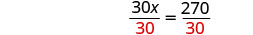
简化。 
通过将 x=9 代入原始方程式,自己检查一下。
解决:\(0.25n + 0.05(n + 5) = 2.95\)
- 回答
-
\(n = 9\)
解决:\(0.10d + 0.05(d -5) = 2.15\)
- 回答
-
\(d = 16\)
关键概念
- 求解具有分数系数的方程的策略
- 找出方程中所有分数的最小公分母。
- 将方程的两边乘以该液晶屏。 这会清除分数。
- 使用求解线性方程的通用策略进行求解。