2.4:使用通用策略求解线性方程
- Page ID
- 204624
在本节结束时,您将能够:
- 使用一般策略求解方程
- 对方程进行分类
在开始之前,请参加这个准备测验。
- 简化:\(−(a−4)\)。
如果你错过了这个问题,请查看练习 1.10.46 - 乘法:\(\frac{3}{2}(12x+20)\)
如果你错过了这个问题,请查看练习 1.10.34。 - 简化:\(5−2(n+1)\)
如果您错过了此问题,请查看练习 1.10.49。 - 乘法:\(3(7y+9)\)
如果你错过了这个问题,请查看练习 1.10.34。 - 乘法:\((2.5)(6.4)\)
如果你错过了这个问题,请查看练习 1.8.19。
使用一般策略求解方程
到目前为止,我们已经解决了求解线性方程的一种特定形式。 现在是制定一种可用于求解任何线性方程的总体策略的时候了。 我们求解的某些方程不需要所有这些步骤即可求解,但许多方程需要解决。
从简化方程的每一面开始,其余步骤就更容易了。
解决:\(-6(x + 3) = 24\)。
- 回答
-





解决:\(5(x + 3)=35\)
- 回答
-
\(x = 4\)
解决:\(6(y - 4) = -18\)
- 回答
-
\(y = 1\)
- 尽可能简化方程的每一面。
使用分布属性删除所有括号。
将相似的术语组合在一起。 - 收集方程一侧的所有变量项。
使用等式的加法或减法属性。 - 收集方程另一侧的所有常量项。
使用等式的加法或减法属性。 - 使变量项的系数等于 1。
使用等式的乘法或除法属性。
陈述方程的解。 - 检查解决方案。 将解替换为原始方程以确保结果是真实的陈述。
解决:\(-(y + 9) = 8\)
- 回答
-
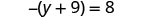
通过分布尽可能简化方程的每一面。 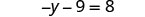
唯一的 y 项位于左侧,因此所有变量项都在方程的左侧。 将两边加上 9 以获得方程右侧的所有常量项。 
简化。 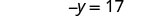
将 −y 重写为 −1y。 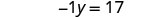
通过将两边除以 −1,使变量项的系数等于 1。 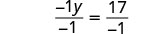
简化。 
查看: 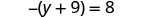
让 y=−17。 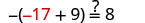
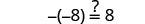
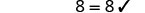
解决:\(-(y + 8) = -2\)
- 回答
-
\(y = -6\)
解决:\(-(z + 4) = -12\)
- 回答
-
\(z = 8\)
解决:\(5(a - 3) + 5 = -10\)
- 回答
-

尽可能简化方程的每一面。 分发。 
将相似的术语组合在一起。 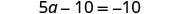
唯一的 a 项位于左侧,因此所有变量项都在方程的一侧。 将两边加上 10 以获得方程另一侧的所有常量项。 
简化。 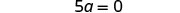
通过将两边除以 55,使变量项的系数等于 11。 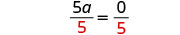
简化。 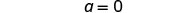
查看: 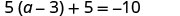
让 a=0。 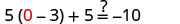
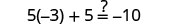
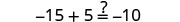
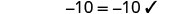
解决:\(2(m - 4) + 3 = -1\)
- 回答
-
\(m = 2\)
解决:\(7(n - 3) - 8 = -15\)
- 回答
-
\(n = 2\)
解决:\(\frac{2}{3}(6m - 3) = 8 - m\)
- 回答
-
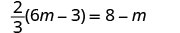
分发。 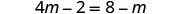
添加 m 以仅获得左边的变量。 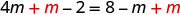
简化。 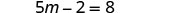
添加 2 可仅在右侧获得常量。 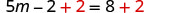
简化。 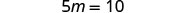
除以 5。 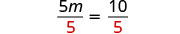
简化。 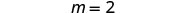
查看: 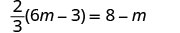
让 m=2。 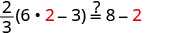
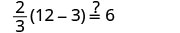
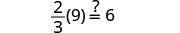
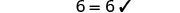
解决:\(\frac{1}{3}(6u + 3) = 7 - u\)
- 回答
-
\(u = 2\)
解决:\(\frac{2}{3}(9x - 12) = 8 + 2x\)
- 回答
-
\(x = 4\)
解决:\(8 - 2(3y + 5) = 0\)
- 回答
-
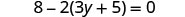
简化-使用分布属性。 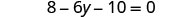
将相似的术语组合在一起。 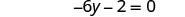
向两边添加 2 以收集右侧的常量。 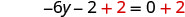
简化。 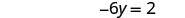
将两边除以 −6−6。 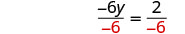
简化。 
查看:让 y=−13。
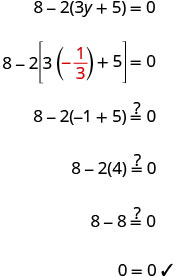
解决:\(12 - 3(4j + 3) = -17\)
- 回答
-
\(j = \frac{5}{3}\)
解决:\(-6 - 8(k - 2) = -10\)
- 回答
-
\(k = \frac{5}{2}\)
解决:\(4(x - 1)-2=5(2x+3)+6\)
- 回答
-
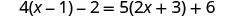
分发。 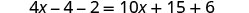
将相似的术语组合在一起。 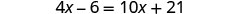
减去 4 倍以后只能得到右侧的变量\(10>4\)。 
简化。 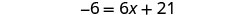
减去 21 得到左边的常量。 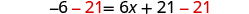
简化。 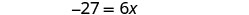
除以 6。 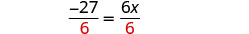
简化。 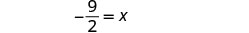
查看: 
让\(x=-\frac{9}{2}\)。 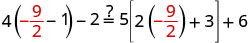
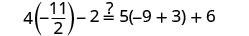
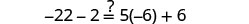
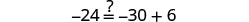
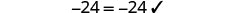
解决:\(6(p-3)-7=5(4p+3)-12\)
- 回答
-
\(p = -2\)
解决:\(8(q +1)-5=3(2q-4)-1\)
- 回答
-
\(q = -8\)
解决:\(10[3 - 8(2s-5)] = 15(40 - 5s)\)
- 回答
-
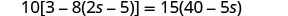
首先从最里面的圆括号中进行简化。 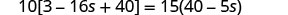
在方括号中组合相似的术语。 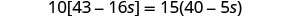
分发。 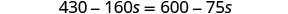
添加 160 以使 s 向右移动。 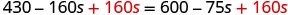
简化。 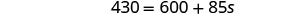
减去 600 得出左边的常量。 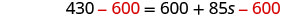
简化。 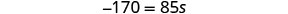
除以。 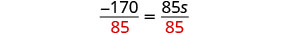
简化。 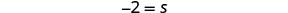
查看: 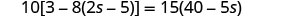
替换 s=−2。 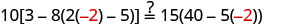
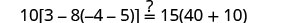
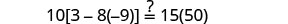
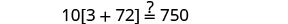
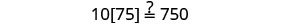
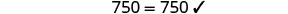
解决:\(6[4−2(7y−1)]=8(13−8y)\)。
- 回答
-
\(y = -\frac{17}{5}\)
解决:\(12[1−5(4z−1)]=3(24+11z)\)。
- 回答
-
\(z = 0\)
解决:\(0.36(100n+5)=0.6(30n+15)\)。
- 回答
-
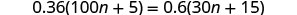
分发。 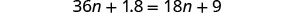
减去 18n 得出左边的变量。 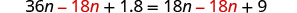
简化。 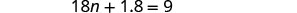
减去 1.8 得出右边的常量。 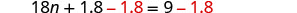
简化。 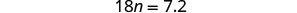
除以。 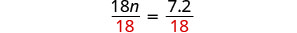
简化。 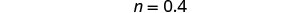
查看: 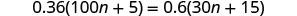
让 n=0.4。 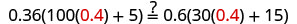
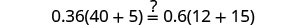
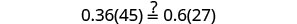
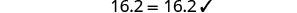
解决:\(0.55(100n+8)=0.6(85n+14)\)。
- 回答
-
\(n = 1\)
解决:\(0.15(40m−120)=0.5(60m+12)\)。
- 回答
-
\(m = -1\)
对方程进行分类
以我们在上一节开头求解的方程为例,7x+8=−13。 我们找到的解是 x=−3。 这意味着当我们将变量 x 替换为值 −3 时,方程 7 x +8=−13 是正确的。 我们在检查解 x=−3 并对 x=−3 求解 7x+8=−13 时证明了这一点。
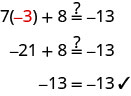
如果我们将 7x+8 计算为不同的 x 值,则左侧不会为 −13。
当我们将变量 x 替换为值 −3 时,方程 7x+8=−13 是正确的,但是当我们用任何其他值替换 x 时则不正确。 方程 7x+8=−13 是否为真取决于变量的值。 像这样的方程被称为条件方程。
到目前为止,我们求解的所有方程都是条件方程。
如果变量的一个或多个值为 true,而变量的所有其他值均为 false 的方程即为条件方程。
现在让我们考虑方程式 2y+6=2 (y+3)。 你知道左边和右边是等同的吗? 让我们看看当我们求解 y 时会发生什么。
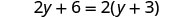 |
|
| 分发。 | 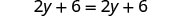 |
| 减去 2y,将 y 变为一边。 | 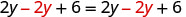 |
| Simplify—y 不见了! | 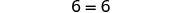 |
但是 6=6 是真的。
这意味着对于 y 的任何值,方程 2y+6=2 (y+3) 都是正确的。 我们说方程的解是所有的实数。 对于像这样的变量的任何值都正确的方程称为恒等式。
对于变量的任何值都正确@@ 的方程称为恒等式。
一个恒等的解是全实数。
当我们求解方程 5z=5z−1 时会发生什么?
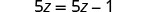 |
|
| 减去 5z,将常数单独放在右边。 | 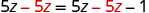 |
| 简化— z 不见了! | 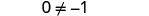 |
但是\(0\neq −1\)。
求解方程 5z=5z−1 会得出错误的陈述 0=−1。 对于 z 的任何值,方程 5z=5z−1 都不成立。它没有解。 没有解的方程或变量的所有值均为假的方程称为矛盾。
对于变量的所有值都为假的方程称为矛盾。
矛盾没有解决办法。
将方程分类为条件方程、恒等式或矛盾方程。 然后陈述解决方案。
\(6(2n−1)+3=2n−8+5(2n+1)\)
回答-
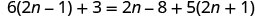
分发。 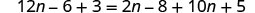
将相似的术语组合在一起。 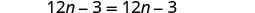
减去 12n,将 nn 放到一边。 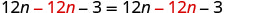
简化。 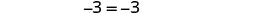
这是真实的陈述。 方程是一个恒等式。
解决方案都是实数。
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:
\(4+9(3x−7)=−42x−13+23(3x−2)\)
回答-
身份;所有实数
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:
\(8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1\)
回答-
身份;所有实数
分类为条件方程、恒等式或矛盾。 然后陈述解决方案。
\(10+4(p−5)=0\)
回答-
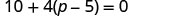
分发。 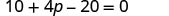
将相似的术语组合在一起。 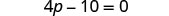
在两边加 10。 
简化。 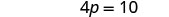
除以。 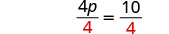
简化。 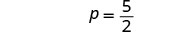
等式在以下情况下是正确的\(p = frac{5}{2}\)。 这是一个条件方程。
解决办法是\(p = frac{5}{2}\)。
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:\(11(q+3)−5=19\)
- 回答
-
条件方程;\ (q =\ frac {9} {11}\
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:\(6+14(k−8)=95\)
- 回答
-
条件方程;\(k = \frac{193}{14}\)
将方程分类为条件方程、恒等式或矛盾方程。 然后陈述解决方案。
\(5m+3(9+3m)=2(7m−11)\)
回答-
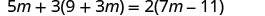
分发。 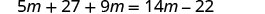
将相似的术语组合在一起。 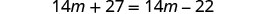
从两边减去 14m。 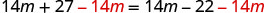
简化。 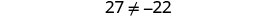
但是\(27\neq −22\)。 这个方程是矛盾的。
它没有解决办法。
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:
\(12c+5(5+3c)=3(9c−4)\)
回答-
矛盾;没有解决办法
将方程归类为条件方程、恒等方程或矛盾方程,然后陈述解:
\(4(7d+18)=13(3d−2)−11d\)
回答-
矛盾;没有解决办法
| 方程的类型 | 当你解决这个问题时会发生什么? | 解决方案 |
|---|---|---|
| 条件方程 | 变量的一个或多个值为 true,所有其他值为 false | 一个或多个值 |
| 身份 | 变量的任何值均为 true | 所有实数 |
| 矛盾 | 变量的所有值均@@ 为 False | 没有解决办法 |
关键概念
- 求解线性方程的通用策略
- 尽可能简化方程的每一面。
使用分布属性删除所有括号。
将相似的术语组合在一起。 - 收集方程一侧的所有变量项。
使用等式的加法或减法属性。 - 收集方程另一侧的所有常量项。
使用等式的加法或减法属性。 - 使变量项的系数等于 1。
使用等式的乘法或除法属性。
陈述方程的解。 - 检查解决方案。
将解替换为原始方程。
- 尽可能简化方程的每一面。


