2.3:求解两边都有变量和常量的方程
- Page ID
- 204640
在本节结束时,您将能够:
- 求解两边都有常数的方程
- 求解两边都有变量的方程
- 求解两边都有变量和常量的方程
求解两边都有常数的方程
在我们到目前为止求解的所有方程中,所有变量项仅在方程的一侧,常量在另一边。 这种情况并非一直发生——因此,现在我们将学会求解变量项或常量项或两者都位于方程两边的方程。
我们的策略将包括选择方程的一侧作为 “可变面”,将方程的另一侧作为 “恒定方”。 然后,我们将使用等式的减法和加法属性将方程一侧的所有变量项组合在一起,将另一侧的常量项组合在一起。
通过这样做,我们将把以两边的变量和常数开头的方程转换为形式\(ax=b\)。 我们已经知道如何使用等式的除法或乘法属性来求解这种形式的方程。
解决:\(7x+8=−13\)。
- 回答
-
在此方程中,变量只能在左侧找到。 将左侧称为 “变量” 侧是有道理的。 因此,右侧将是 “不变” 的一面。 我们将在方程式上方写下标签,以帮助我们记住发生了什么。
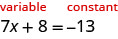
由于左侧是 “xx” 或可变边,因此 8 不合适。 我们必须通过减去 8 来 “撤消” 加 8,为了保持相等,我们必须从两边减去 8。
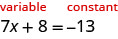
使用等式的减法属性。 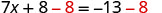
简化。 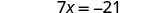
现在所有变量都在左边,常量在右边。 这个方程看起来像你之前学会求解的方程式。 使用平等的分割属性。 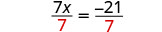
简化。 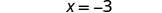
查看: 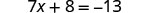
让 x=−3。 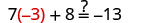
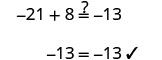
解决:\(3x+4=−8\)。
- 回答
-
\(x=−4\)
解决:\(5a+3=−37\)。
- 回答
-
\(a=−8\)
解决:\(8y−9=31\)。
- 回答
-
注意,变量只在方程的左边,所以我们将这边称为 “变量” 边,右边是 “常量” 边。 由于左侧是 “变量” 边,因此 9 不合适。 从 8y 中减去,因此 “撤消” 减法,请在两边加上 9。 记住,无论你在左边做什么,都必须向右做。
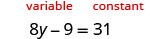
在两边加上 9。 
简化。 
变量现在在一边,常量在另一边。
我们像以前一样从这里继续。将两边除以 8。 
简化。 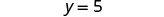
查看: 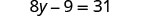
让 y=5。 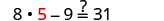
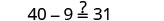
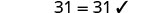
解决:\(5y−9=16\)。
- 回答
-
\(y=5\)
解决:\(3m−8=19\)。
- 回答
-
\(m = 9\)
求解两边都有变量和常量的方程
下一个示例将是第一个在方程两边都有变量和常量的示例。 求解这个方程可能需要几个步骤,因此我们需要一个明确而有条理的策略。
解决:\(9x=8x−6\)。
- 回答
-
这里变量在两边,但常量只出现在右边,所以让我们把右边设为 “常量” 边。 然后左侧将是 “变量” 边。

我们不希望右边有任何 x,所以从两边减去 8 倍。 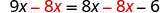
简化。 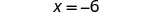
我们成功地在一侧获取了变量,在另一侧获得了常量,并获得了解。 查看: 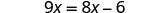
让 x=−6。 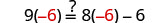
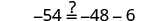
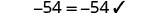
解决:\(6n=5n−10\)。
- 回答
-
\(n = -10\)
解决:\(-6c = -7c - 1\)
- 回答
-
\(c = -1\)
解决:\(5y - 9 = 8y\)
- 回答
-
唯一的常量在左边,y 在两边。 让我们把常量留在左边,把变量放在右边。
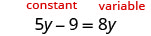
从两边减去 5y。 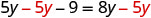
简化。 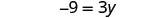
右边有 y,左边是
常量。 将两边除以 3。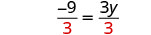
简化。 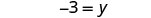
查看: 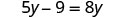
让\(y=−3\)。 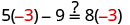
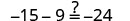
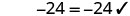
解决:\(3p−14=5p\)。
- 回答
-
\(p = -7\)
解决:\(8m + 9 = 5m\)
- 回答
-
\(m = -3\)
解决:\(12x = -x + 26\)
- 回答
-
唯一的常量在右边,所以让左边是 “变量” 边。
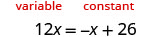
通过在两边添加 x 来移除右侧的 −x。 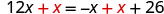
简化。 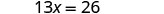
所有 x 都在左边,常量在右边。 将两边除以 13。 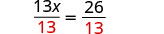
简化。 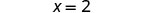
解决:\(12j = -4j + 32\)
- 回答
-
\(j = 2\)
解决:\(8h = -4h + 12\)
- 回答
-
\(h = 1\)
求解两边都有变量和常量的方程
下一个示例将是第一个在方程两边都有变量和常量的示例。 求解这个方程可能需要几个步骤,因此我们需要一个明确而有条理的策略。
解决:\(7x + 5 = 6x + 2\)
- 回答
-





解决:\(12x+8=6x+2\)。
- 回答
-
\(x=−1\)
解决:\(9y+4=7y+12\)。
- 回答
-
\(y=4\)
我们将在下面列出步骤,以便您可以轻松参考它们。 但是我们称之为 “入门策略”,因为我们将在本章后面添加一些步骤。
- 选择哪一侧将是 “变量” 边,另一侧将是 “恒定” 边。
- 使用等式的加法或减法属性将变量项收集到方程的 “变量” 侧。
- 使用等式的加法或减法属性收集方程另一侧的所有常量。
- 使用相等的乘法或除法属性使变量的系数等于 1。
- 通过将其替换为原始方程来检查解。
在步骤 1 中,一种有用的方法是将 “变量” 侧设置为具有较大系数的变量的一侧。 这通常会使算术更容易。
解决:\(8n−4=−2n+6\)。
- 回答
-
在第一步中,通过比较每边变量的系数来选择变量边。
因此\(8>−2\),将左侧设为 “变量” 边。 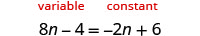
我们不希望变量项放在右边,在两边加上 2n,只在右边留下常量。 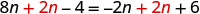
将相似的术语组合在一起。 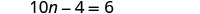
我们不希望左侧有任何常量,所以在两边都加 4。 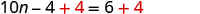
简化。 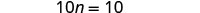
变量项在左边,常量项在右边。 要使 nn 的系数为一,请将两边除以 10。 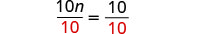
简化。 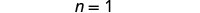
查看: 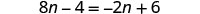
让 n=1。 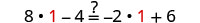

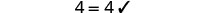
解决:\(8q - 5 = -4q + 7\)
- 回答
-
\(q = 1\)
解决:\(7n - 3 = n + 3\)
- 回答
-
\(n = 1\)
解决:\(7a -3 = 13a + 7\)
- 回答
-
在第一步中,通过比较每边变量的系数来选择变量边。
从 13>7 开始,将右侧设为 “可变” 边,将左侧设为 “恒定” 边。
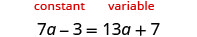
从两边减去 7a 以删除左边的变量项。 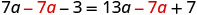
将相似的术语组合在一起。 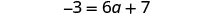
从两边减去 7 以移除右边的常数。 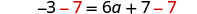
简化。 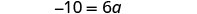
将两边除以 6,使 1 成为 a 的系数。 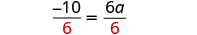
简化。 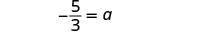
查看: 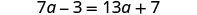
让\(a=−\frac{5}{3}\)。 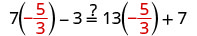
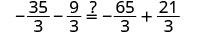
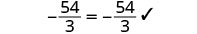
解决:\(2a - 2 = 6a + 18\)
- 回答
-
\(a = -5\)
解决:\(4k -1 = 7k + 17\)
- 回答
-
\(k = -6\)
在最后一个例子中,我们可以将左侧设为 “变量” 边,但它会导致变量项的系数为负。 (试试吧!) 虽然我们可以处理负面因素,但在处理正面因素时出错的可能性较小。 上面概述的策略有助于避免负面影响!
要用分数求解方程,我们只需按照策略的步骤得到解即可!
解决:\(\frac{4}{5}x + 6 = \frac{1}{4}x - 2\)
- 回答
-
因此\(\frac{5}{4} > \frac{1}{4}\),将左侧设为 “变量” 边,将右侧设为 “恒定” 边。
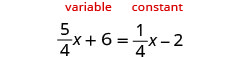
\(\frac{1}{4}x\)从两边减去。 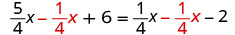
将相似的术语组合在一起。 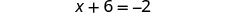
从两边减去 6。 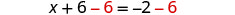
简化。 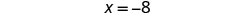
查看:让\(x = -8\)
\(\begin{array} {ccc} {\frac{5}{4}x + 6} &{=} &{\frac{1}{4}x - 2} \\ {\frac{5}{4}(-8) + 6} &{\stackrel{?}{=}} &{\frac{1}{4}(-8) - 2} \\ {-10 + 6} &{\stackrel{?}{=}} &{-2 - 2} \\ {-4} &{=} &{-4\checkmark} \end{array}\)
解决:\(\frac{7}{8}x - 12 = -\frac{1}{8}x - 2\)
- 回答
-
\(x = 10\)
解决:\(\frac{7}{6}x + 11 = \frac{1}{6}y + 8\)
- 回答
-
\(y = -3\)
我们将使用相同的策略来找到带有小数的方程的解。
解决:\(7.8x+4=5.4x−8\)。
- 回答
-
因此\(7.8>5.4\),将左侧设为 “变量” 边,将右侧设为 “恒定” 边。
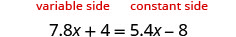
从两边减去 5.4 倍。 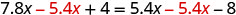
将相似的术语组合在一起。 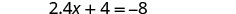
从两边减去 4。 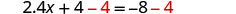
简化。 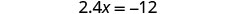
使用平等的分割属性。 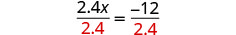
简化。 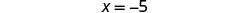
查看: 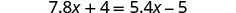
让\(x=−5\) 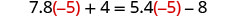
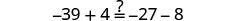
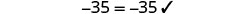
解决:\(2.8x + 12 = -1.4x - 9\)
- 回答
-
\(x = -5\)
解决:\(3.6y + 8 = 1.2y - 4\)
- 回答
-
\(y = -5\)
关键概念
- 求解方程两边都有变量和常数的方程的初始策略
- 选择哪一侧将是 “变量” 边,另一侧将是 “恒定” 边。
- 使用等式的加法或减法属性将变量项收集到方程的 “变量” 侧。
- 使用等式的加法或减法属性收集方程另一侧的所有常量。
- 使用相等的乘法或除法属性使变量的系数等于 1。
- 通过将其替换为原始方程来检查解。


