2.2:使用等式的除法和乘法属性求解方程
- Page ID
- 204674
在本节结束时,您将能够:
- 使用等式的除法和乘法属性求解方程
- 求解需要简化的方程
- 转换为方程并求解
- 翻译和解决应用程序
使用等式的除法和乘法属性求解方程
你可能已经注意到,到目前为止,我们求解的所有方程都是形式\(x+a=b\)或\(x−a=b\)。 我们能够通过将方程旁边的常量项与变量相加或减去来分离变量。 现在我们将看到如何求解变量乘以常量的方程,因此需要除法才能分离变量。
让我们用图中的信封和计数器再来看看我们的拼图\(\PageIndex{1}\)。
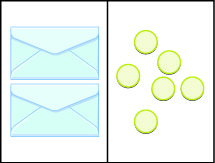
在插图中,有两个相同的信封包含相同数量的计数器。 请记住,工作空间的左侧必须等于右侧,但左侧的计数器在信封中 “隐藏”。 那么每个信封里有多少个计数器呢?
我们如何确定这个数字? 我们必须将右侧的柜台分成两组,大小相同,以便与左侧的两个信封相对应。 分为 2 个相等组的 6 个计数器在每组中有 3 个计数器(从那以后\(6\div 2=3\))。
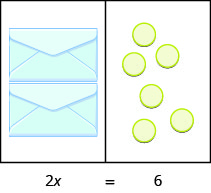
什么方程模拟了图中所示的情况\(\PageIndex{2}\)? 有两个信封,每个信封包含 xx 个计数器。 两个信封总共必须包含 6 个计数器。
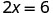 |
|
| 如果我们把方程的两边除以 2,就像我们对信封和计数器所做的那样, | 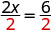 |
| 我们得到: | 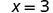 |
我们发现每个信封包含 3 个计数器。 这会检查吗? 我们知道\(2\cdot 3=6\),所以行得通! 两个信封中每个信封中的三个计数器等于六个!
这个例子引出了 “平等分割财产”。
对于任意数字 a、b 和 c\(c\neq 0\),
\[\begin{array} {llll} {\text { If }} &{a} &{=} &{b} \\ {\text {then}} & {\frac { a } { c }} &{=} &{\frac { b } { c }} \end{array}\]
当你将方程的两边除以任何非零数时,你仍然相等。
进行操纵数学活动 “平等的除法属性” 将有助于你更好地了解如何使用平等的除法属性求解方程。
求解方程的目标是 “撤消” 对变量的操作。 在下一个示例中,将变量乘以 5,因此我们将两边除以 5 以 “撤消” 乘法。
解决:\(5x=−27\)。
- 回答
-
要隔离 x,请将乘以 5 “撤消”。 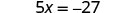
除以 “撤消” 乘法。 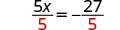
简化。 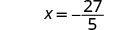
查看: 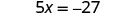
替换\(-\frac{27}{5}\) x。 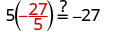
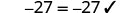
既然这是真实的陈述,\(x = -\frac{27}{5}\)
就是解决方案\(5x=−27\)。
解决:\(3y=−41\)。
- 回答
-
\(y = -\frac{41}{3}\)
解决:\(4z=−55\)。
- 回答
-
\(y = -\frac{55}{4}\)
考虑这个方程式\(\frac{x}{4} = 3\)。 我们想知道用什么数字除以 4 得出 3。 因此,要 “撤消” 除法,我们需要乘以 4。 相等的乘法属性将允许我们做到这一点。 这个属性表示,如果我们从两个相等的量开始,然后将两个数乘以相同的数字,则结果相等。
对于任何数字 a、b 和 c,
\[\begin{array} {llll} {\text {If}} &{a} & {=} &{b} \\ {\text {then}} &{a c} &{=} &{b c} \end{array}\]
如果将方程的两边乘以相同的数字,则仍然相等。
解决:\(\frac{y}{-7} = -14\)
- 回答
-
这里 y 除以 −7。 我们必须乘以 −7 才能分离 y。

将两边乘以 −7。 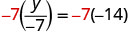
乘。 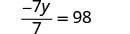
简化。 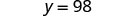
查看:\(\frac{y}{-7} = -14\) 替代 y=98。 
除以。 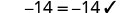
解决:\(\frac{a}{-7} = -42\)
- 回答
-
\(a = 294\)
解决:\(\frac{b}{-6} = -24\)
- 回答
-
\(b = 144\)
解决:\(-n = 9\)
- 回答
-
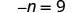
记住 −n 等同于 −1n。 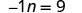
将两边除以 −1。 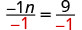
除以。 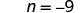
请注意,还有其他两种求解 −n=9 的方法。 我们也可以通过将两边乘以 −1 以及取两边的相反值来求解这个方程。 查看: 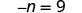
替换 n=−9。 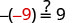
简化。 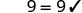
解决:\(−k=8\)。
- 回答
-
\(k = -8\)
解决:\(−g=3\)。
- 回答
-
\(g = -3\)
解决:\(\frac{3}{4}x = 12\)
- 回答
-
由于数字及其倒数的乘积为 1,我们的策略是通过乘以的倒数来隔离 x\(\frac{3}{4}\)。
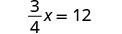
乘以的倒数\(\frac{3}{4}\)。 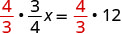
倒数乘以 1。 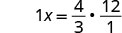
乘。 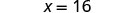
请注意,我们可以将方程的两边除\(\frac{3}{4}\)以\(\frac{3}{4}x = 12\)分离 x。虽然这行得通,但大多数人会发现乘以倒数更容易。 查看: 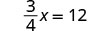
替代\(x=16\)。 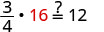
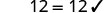
解决:\(\frac{2}{5}n=14\)。
- 回答
-
\(n = 35\)
解决:\(\frac{5}{6}y=15\)。
- 回答
-
\(y = 18\)
在下一个示例中,所有变量项都在方程的右侧。 与往常一样,我们求解方程的目标是隔离变量。
解决:\(\frac{8}{15} = -\frac{4}{5}x\)
- 回答
-
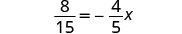
乘以的倒数\(-\frac{4}{5}\)。 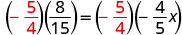
倒数乘以 1。 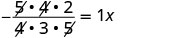
乘。 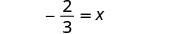
查看: 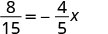
让\(x = -\frac{2}{3}\)。 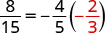
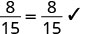
解决:\(\frac{9}{25} = -\frac{4}{5}z\)
- 回答
-
\(z = - \frac{9}{5}\)
\(\frac{5}{6} = -\frac{8}{3}r\)
- 回答
-
\(r = -\frac{5}{16}\)
求解需要简化的方程
许多方程起初比我们一直在研究的方程要复杂得多。
对于这些更复杂的方程,第一步是尽可能简化方程的两面。 这通常涉及合并相似的术语或使用分配属性。
解决:\(14−23=12y−4y−5y\)。
- 回答
-
首先简化方程的每一面。
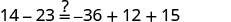
简化每一面。 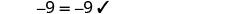
将两边除以 3 以分离 y。 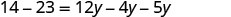
除以。 
查看: 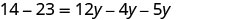
替代\(y=−3\)。 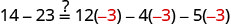
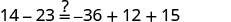
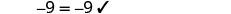
解决:\(18−27=15c−9c−3c\)。
- 回答
-
\(c=−3\)
解决:\(18−22=12x−x−4x\)。
- 回答
-
\(x = -\frac{4}{7}\)
解决:\(−4(a−3)−7=25\)。
- 回答
-
在这里,我们将首先使用分布属性来简化方程的每一面。
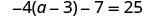
分发。 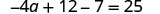
简化。 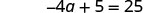
简化。 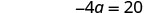
将两边除\(-4\)以隔离 a。 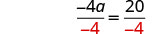
除以。 
查看: 
替代\(a = -5\) 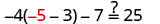
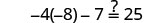
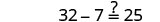
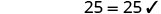
解决:\(−4(q−2)−8=24\)。
- 回答
-
\(q=−6\)
解决:\(−6(r−2)−12=30\)。
- 回答
-
\(r=−5\)
现在,我们已经介绍了相等的所有四个属性——减法、加法、除法和乘法。 为了便于参考,我们将在此处将它们全部列出。
当你从方程的两边加、减、乘或除以相同的量时,你仍然相等。
\ [\ begin {array} {ll} {\ textbf {平等的减法属性}} &
{\ textbf {平等的加法属性}}\\ {\ text {对于任何实数 a、b 和 c,}}
\\ {\ text {if} a = b,}
\\ {\ text {then} a-c = b-c} & {\ text {then} a + c = b + c}
\\ {\ textbf {平等的除法属性}} & {\ textbf
{相等的乘法属性}}\\ {\ text {对于任何实数 a、b 和 c,}}
\\ {\ text {if} a = b,} & {\text {if} a = b,}
\\ {\ text {then} a-c = b-c} & {\ text {then} a + c = b + c}
\ end {array}\]
当你从方程的两边加、减、乘或除以相同的量时,你仍然相等。
转换为方程并求解
在接下来的几个例子中,我们将把句子翻译成方程式,然后求解方程。 您可能需要查看上一章中的翻译表。
平移并求解:数字 143 是 −11 和 y 的乘积。
- 回答
-
翻译。 
除以 −11。 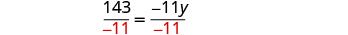
简化。 
查看:
\[\begin{array} {lll} {143} &{=} &{-11y} \\ {143} &{\stackrel{?}{=}} &{-11(-13)} \\ {143} &{=} &{143\checkmark} \end{array}\]
平移并求解:数字 132 是 −12 和 y 的乘积。
- 回答
-
132=−12y;y=−11
平移并求解:数字 117 是 −13 和 z 的乘积。
- 回答
-
117=−13z;z=−9
平移并求解:n 除以 8 等于 −32。
- 回答
-
首先将句子翻译成方程式。
翻译。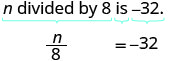
将两边乘以 8。 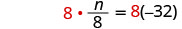
简化。 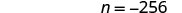
查看: nn 除以 8 等于 −32 吗? 让\(n=−256\)。 −256 除以 88 等于 −32 吗? 翻译。 \(\frac{-256}{8} \stackrel{?}{=} -32\) 简化。 \(−32=−32\checkmark\)
平移并求解:nn 除以 7 等于 −21。
- 回答
-
\(\frac{n}{7}=−21; n=−147\)
平移并求解:n 除以 8 等于 −56。
- 回答
-
\(\frac{n}{8}=−56;n=−448\)
翻译并求解:yy 和 −4 的商为 68。
- 回答
-
首先将句子翻译成方程式。
翻译。 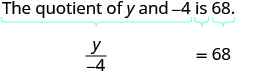
将两边乘以 -4。 
简化。 
查看: y 和 −4 的商等于 68 吗? 让 y=−272。 −272 和 −4 的商等于 68 吗? 翻译。 \(\frac{-272}{-4} \stackrel{?}{=} 68\) 简化。 \(68 = 68\checkmark\)
平移并求解:q 和 −8 的商为 72。
- 回答
-
\(\frac{q}{-8}=72;q=−576\)
翻译并求解:p 和 −9 的商为 81。
- 回答
-
\(\frac{p}{-9}=81;p=−729\)
平移并求解:p 的四分之三为 18。
- 回答
-
首先将句子翻译成方程式。 请记住,“of” 转换为乘法。
翻译。 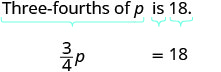
将两边乘以\(\frac{4}{3}\)。 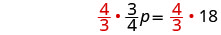
简化。 
查看: p 的四分之三等于 18 吗? 假设 p = 24。 24 的四分之三等于 18 吗? 翻译。 \(\frac{3}{4}\cdot 24 \stackrel{?}{=} 18\) 简化。 \(18=18\checkmark\)
平移并求解:f 的五分之二为 16。
- 回答
-
\(\frac{2}{5}f=16; f=40\)
平移并求解:f 的四分之三为 21。
- 回答
-
\(\frac{3}{4}f=21; f=28\)
平移并求解:八分之三和 x 的总和为一半。
- 回答
-
首先将句子翻译成方程式。
翻译。 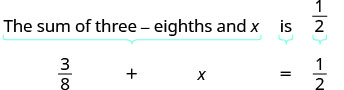
\(\frac{3}{8}\)从两边减去。 
使用公分母简化和重写分数。 
简化。 
查看: 八分之三和 x 的总和是否等于一半? 让\(x=\frac{1}{8}\)。 八分之三和八分之一的总和等于一半吗? 翻译。 \(\frac{3}{8} + \frac{1}{8} \stackrel{?}{=} \frac{1}{2}\) 简化。 \(\frac{4}{8} \stackrel{?}{=} \frac{1}{2}\) 简化。 \(\frac{1}{2} = \frac{1}{2} \checkmark\)
平移并求解:八分之五和 x 的总和为四分之一。
- 回答
-
\(\frac{5}{8} + x = \frac{1}{4}; x = -\frac{3}{8}\)
平移并求解:四分之三和 x 的总和为六分之五。
- 回答
-
\(\frac{3}{4} + x = \frac{5}{6}; x = \frac{1}{12}\)
翻译和解析应用程序
要使用等式的除法和乘法属性求解应用程序,我们将按照上一节中使用的相同步骤进行操作。 我们将仅用一句话重述问题,分配一个变量,然后将该句转换为要解的方程。
Denae 以 10.74 美元的价格购买了 6 磅的葡萄。 一磅葡萄的成本是多少?
- 回答
-
\[\begin{array} {ll} {\text{What are you asked to find?}} &{\text{The cost of 1 pound of grapes}} \\\\ {\text{Assign a variable.}} &{\text{Let c = the cost of one pound.}} \\\\ {\text{Write a sentence that gives the}} &{\text{The cost of 6 pounds is }$10.74} \\ {\text{information to find it.}} &{} \\\\ {\text{Translate into an equation.}} &{6c = 10.74} \\ {\text{Solve.}} &{\frac{6c}{c} = \frac{10.74}{6}} \\ {} &{c = 1.79} \\\\ {} &{\text{The grapes cost }$ 1.79 \text{ per pound.}} \\ \\ {\text{Check: If one pound costs }$1.79, do} &{} \\ {\text{6 pounds cost }$ 10.74?} &{} \\\\ {6(1.79) \stackrel{?}{=} 10.74} &{} \\ {10.74 = 10.74\checkmark} &{} \end{array}\]
翻译并解决:
阿里安娜花9.36美元买了一个24包的水瓶。 一瓶水的成本是多少?
- 回答
-
0.39 美元
翻译并解决:
在JB的保龄球馆,6个人可以花34.98美元在一条车道上玩游戏。 每个人的费用是多少?
- 回答
-
5.83 美元
安德烈亚斯花了12,000美元买了一辆二手车。 因为这辆车已经使用了4年,所以它的价格是\(\frac{3}{4}\)新车时的原价。 这辆车的原价是多少?
- 回答
-
\[\begin{array} {ll} {\text{What are you asked to find?}} &{\text{The original price of the car}} \\\\ {\text{Assign a variable.}} &{\text{Let p = the original price.}} \\\\ {\text{Write a sentence that gives the}} &{$12000\text{ is }\frac{3}{4} \text{ of the original price.}} \\ {\text{information to find it.}} &{} \\\\ {\text{Translate into an equation.}} &{12000 = \frac{3}{4}p} \\ {} &{\frac{3}{4}(12000) = \frac{4}{3}\cdot \frac{3}{4}p}\\ {}&{16000 = p} \\{\text{Solve.}} &{} \\\\ {} &{\text{The original cost of the car was }$ 16000.} \\ \\ {\text{Check: Is }\frac{3}{4} \text{ of }$16000 \text{ equal to }$12000} &{} \\\\ {\frac{3}{4}\cdot 16000 \stackrel{?}{=} 12000} &{} \\ {12000 = 12000\checkmark} &{} \end{array}\]
翻译并解决:
梅塔房屋的年度财产税为1,800美元,根据房屋\(\frac{15}{1000}\)的评估价值计算。 梅塔房屋的评估价值是多少?
- 回答
-
120000 美元
翻译并解决:
斯特拉在她的花园里\(\frac{2}{3}\)种了14平花。 她需要多少平鲜花才能填满整个花园?
- 回答
-
21 个平底鞋
关键概念
- 相@@ 等的除法属性-适用于任意数字 a、b 和 c,以及 i\(c\neq 0\) f\(a=b\)、then\(\frac{a}{c} = \frac{b}{c}\)。
当你将方程的两边除以任何非零数时,你仍然相等。 - 相@@ 等的乘法属性 —对于任何数字 a、b 和 c,if\(a=b\),then\(ac = bc\)。
如果将方程的两边乘以相同的数字,则仍然相等。


