1.9: 实数

学习目标

在本节结束时，您将能够：

• 使用平方根简化表达式
• 识别整数、有理数、非理数和实数
• 在数字行上找到分数
• 在数字行上找到小数

注意

对本节所涵盖主题的更详尽的介绍可在 Prealgebra 章节 “小数和实数的属性” 中找到。

使用平方根简化表达式

请记住，当一个数字\(n\)乘以自身时，我们将其写入\(n^{2}\)和读取 “\(n\)平方”。 结果被称为的平方\(n\)。 例如，

\[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]

同样，121 是 11 的平方，因为\(11^{2}\)是 121。

数字的平方

如果\(n^{2}=m\)，则\(m\)是的平方\(n\)。

注意

进行操纵数学活动 “平方数” 将有助于你更好地理解完美平方数。

完成下表以显示计数数字 1 到 15 的平方。

图\(\PageIndex{1}\)

第二行中的数字称为完美平方数。 学会识别完美的平方数会很有帮助。

计数数字的平方是正数。 那负数的平方呢？ 我们知道，当两个数字的符号相同时，它们的乘积是正数。 因此，任何负数的平方也是正数。

\[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]

你有没有注意到这些方格和正数的平方是一样的？

有时我们需要反向看数字和它们的平方之间的关系。 因为\(10^{2}=100\)，我们说 100 是 10 的平方。 我们还说 10 是 100 的平方根。 平方为 mm 的数字称为平方根\(m\)。

数字的平方根

如果\(n^{2}=m\)，\(n\)则为的平方根\(m\)。

\((−10)^{2}=100\)另请注意，的平方根\(−10\)也是如此\(100\)。 因此，\(10\)和\(−10\)都是的平方根\(100\)。

因此，每个正数都有两个平方根——一个正数和一个负数。 如果我们只想要一个正数的正平方根呢？ 激进符号\(\sqrt{m}\)，表示正平方根。 正平方根称为主平方根。 当我们使用激进符号时，这总是意味着我们想要主平方根。

我们还使用激进符号来表示零的平方根。 因为\(0^{2}=0, \sqrt{0}=0\)。 请注意，零只有一个平方根。

平方根表示法

\(\sqrt{m}\)被读为 “的平方根\(m\)”

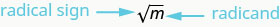
如果\(m = n^{2}\)，那么\(\sqrt{m} = n\)，对于\(n\geq 0\)。

的平方根是正数\(m\)\(\sqrt{m}\)，其平方为\(m\)。

由于 10 是 100 的主平方根，我们这样写\(\sqrt{100}=10\)。 您可能需要填写下表以帮助您识别平方根。

图\(\PageIndex{2}\)

练习\(\PageIndex{1}\)

简化：

1. \(\sqrt{25}\)
2. \(\sqrt{121}\)

回答

1. \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
2. \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]

练习\(\PageIndex{2}\)

简化：

1. \(\sqrt{36}\)
2. \(\sqrt{169}\)

回答

1. 6
2. 13

练习\(\PageIndex{3}\)

简化：

1. \(\sqrt{16}\)
2. \(\sqrt{196}\)

回答

1. 4
2. 14

我们知道每个正数都有两个平方根，激进符号表示正数。 我们写\(\sqrt{100)=10\)。 如果我们想找到一个数字的负平方根，我们在激进符号前面放一个负数。 例如，\(-\sqrt{100)=-10\)。 我们读\(-\sqrt{100)\)作 “与 10 的平方根相反”。

练习\(\PageIndex{4}\)

简化：

1. \(-\sqrt{9}\)
2. \(-\sqrt{144}\)

回答

1. \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
2. \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]

练习\(\PageIndex{5}\)

简化：

1. \(\sqrt{16}\)
2. \(\sqrt{196}\)

回答

1. −2
2. −15

练习\(\PageIndex{6}\)

简化：

1. \(\sqrt{16}\)
2. \(\sqrt{196}\)

回答

1. −9
2. −10

识别整数、有理数、非理数和实数

我们已经将数字描述为计数数字 s、整数 s 和整数。 这些类型的数字有什么区别？

\[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]

如果我们从所有整数开始，然后包括所有分数，我们会得到什么类型的数字？ 我们会得到的数字构成了有理数的集合。 有理数是一个可以写成两个整数之比的数字。

有理数

有理数是形式的数字\(\dfrac{p}{q}\)，其中 p 和 q 是整数，\(q \neq 0\)

有理数可以写成两个整数的比率。

所有有符号分数，例如\(\dfrac{4}{5}\)、\(-\dfrac{7}{8}\)\(\dfrac{13}{4}\)、，\(-\dfrac{20}{3}\)都是有理数。 每个分子和每个分母都是一个整数。

整数是有理的数字吗？ 为了确定一个整数是否是有理数，我们尝试将其写成两个整数的比率。 每个整数可以通过多种方式写成整数的比例。 例如，3 等效于\(\dfrac{3}{1}\)\(-\dfrac{6}{2}\)、\(\dfrac{9}{3}\)、\(\dfrac{12}{4}\)、\(-\dfrac{15}{5} \ldots\)

将整数写成整数比率的一种简单方法是将其写成分母为一的分数。

\[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]

由于任何整数都可以写成两个整数的比率，因此所有整数都是有理数！ 请记住，计数数字和整数也是整数，因此它们也是有理的。

那小数呢？ 他们是理性的吗？ 让我们看几个，看看是否可以将它们中的每一个写成两个整数的比率。

我们已经看到整数是有理数。 整数\(−8\)可以写成十进制\(−8.0\)。 因此，很明显，一些小数是合理的。

想想十进制\(7.3\)。 我们可以把它写成两个整数的比率吗？ 因为\(7.3\)意思是\(7\dfrac{3}{10}\)，我们可以把它写成一个不恰当的分数，\(\dfrac{73}{10}\)。 整数\(73\)和的比率\(7.3\)也是如此\(10\)。 它是一个有理的数字。

通常，任何在数位后结尾的小数（例如\(7.3\)或\(−1.2684\)）都是有理数。 当将十进制写成分数时，我们可以使用最后一位数字的位值作为分母。

练习\(\PageIndex{7}\)

写成两个整数的比率：

1. −27
2. 7.31

回答

1. \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
2. \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]

因此，我们可以看到 −27 和 7.31 都是有理数，因为它们可以写成两个整数的比率。

练习\(\PageIndex{8}\)

写成两个整数的比率：

1. −24
2. 3.57

回答

1. \(\dfrac{-24}{1}\)
2. \(\dfrac{357}{100}\)

练习\(\PageIndex{9}\)

写成两个整数的比率：

1. −19
2. 8.41

回答

1. \(\dfrac{-19}{1}\)
2. \(\dfrac{841}{100}\)

让我们来看看我们知道是合理的数字的十进制形式。

我们已经看到，每个整数都是有理数，因为\(a = \dfrac{a}{1}\)对于任何整数来说，都是\(a\)。 我们还可以通过添加小数点和零将任何整数更改为十进制。

\[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]

我们还看到，每个分数都是一个有理的数字。 看看我们上面考虑的分数的十进制形式。

\[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]

这些例子告诉我们什么？

每个有理数既可以写成整数的比率（\(\dfrac{p}{q}\)，其中 p 和 q 是整数和\(q\neq 0\)），也可以写成停止或重复的十进制。

以下是我们在上面看过的以整数比率和十进制表示的数字：

桌子\(\PageIndex{1}\)

分数					整数
数字	\(\frac{4}{5}\)	\(\frac{7}{8}\)	\(\frac{13}{4}\)	\(-\frac{20}{3}\)	−2	−1	0	1	2	3
整数比率	\(\frac{4}{5}\)	\(\frac{7}{8}\)	\(\frac{13}{4}\)	\(-\frac{20}{3}\)	\(-\frac{2}{1}\)	\(-\frac{1}{1}\)	\(\frac{0}{1}\)	\(\frac{1}{1}\)	\(\frac{2}{1}\)	\(\frac{3}{1}\)
十进制形式	0.8	−0.875	3.25	\(−6.\overline{6}\)	−2.0	−1.0	0.0	1.0	2.0	3.0

有理数

有理数是形式的数字\(\frac{p}{q}\)，其中 p 和 q 是整数，\(q\neq 0\)

它的十进制形式停止或重复。

有没有不停止或重复的小数？ 是的！

数字\(\pi\)（希腊字母 pi，发音为 “pie”）在描述圆圈时非常重要，它采用十进制形式，不会停止或重复。

\[\pi =3.141592654\ldots\]

我们甚至可以创建一个不会停止或重复的十进制模式，例如

\[2.01001000100001\ldots\]

十进制形式不停止或重复的数字不能写成整数的分数。 我们称这些数字为非理性。

非理性数

非理数是不能写成两个整数之比的数字。

它的十进制形式不会停止，也不会重复。

让我们总结一种方法，我们可以用来确定一个数字是有理的还是非理性的。

理性还是非理性？

如果是数字的十进制形式

• 重复或停止，数字是合理的。
• 不重复也不停止，这个数字是不合理的。

练习\(\PageIndex{10}\)

给定数字\(0.58\overline{3}, 0.47, 3.605551275\ldots\)列表

1. 有理数
2. 非理性数字。

回答

1. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
2. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]

练习\(\PageIndex{11}\)

对于给定的数字，请列出

1. 有理数
2. 非理性数字：\(0.29, 0.81\overline{6}, 2.515115111….\)

回答

1. \(0.29, 0.81\overline{6}\)
2. \(2.515115111….\)

练习\(\PageIndex{12}\)

对于给定的数字，请列出

1. 有理数
2. 非理性数字：\(2.6\overline{3}, 0.125, 0.418302…\)

回答

1. \(2.6\overline{3}, 0.125\)
2. \(0.418302…\)

练习\(\PageIndex{13}\)

对于给定的每个数字，确定它是合理的还是非理性的：

1. \(\sqrt{36}\)
2. \(\sqrt{44}\)

回答

1. 认识到 36 是一个完美的正方形，因为\(6^{2} = 36\)。 因此\(\sqrt{36} = 6\)，\(\sqrt{36}\)是合理的。
2. 记住这一点\(6^{2} = 36\)\(7^{2} = 49\)，所以\(44\)不是一个完美的正方形。 因此，十进制形式永远\(\sqrt{44}\)不会重复，也永远不会停止，因此\(\sqrt{44}\)是不合理的。

练习\(\PageIndex{14}\)

对于给定的每个数字，确定它是合理的还是非理性的：

1. \(\sqrt{81}\)
2. \(\sqrt{17}\)

回答

1. 合理的
2. 不合逻辑的

练习\(\PageIndex{15}\)

对于给定的每个数字，确定它是合理的还是非理性的：

1. \(\sqrt{116}\)
2. \(\sqrt{121}\)

回答

1. 不合逻辑的
2. 合理的

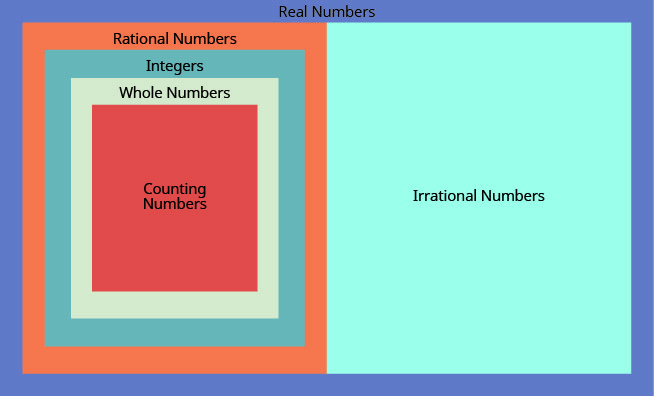
我们已经看到，所有计数数都是整数，所有整数都是整数，所有整数都是有理数。 非理性数是十进制形式不停止且不重复的数字。 当我们将有理数和非理数放在一起时，我们得到了一组实数 s。

实数

实数是有理或非理性的数字。

我们在基本代数中使用的所有数字都是实数。 该图\(\PageIndex{3}\)说明了我们在本节中讨论的数字集是如何组合在一起的。

图\(\PageIndex{3}\)：此图表显示了构成实数集的数字集。 “实数” 一词对你来说似乎很奇怪吗？ 有没有不是 “真实” 的数字，如果有，它们可能是什么？

我们可以简化\(\sqrt{-25}\)吗？ 有数字的正方形\(−25\)吗？

\[(\quad)^{2}=−25?\]

到目前为止，我们处理的数字中没有一个是正方形\(−25\)。 为什么？ 任何正数的平方均为正数。 任何负数平方均为正数。 所以我们说没有实数等于\(\sqrt{-25}\)。

负数的平方根不是实数。

练习\(\PageIndex{16}\)

对于给定的每个数字，确定它是实数还是不是实数：

1. \(\sqrt{-169}\)
2. \(-\sqrt{64}\)

回答

1. 没有实数的平方是\(−169\)。 因此，\(\sqrt{-169}\)不是实数。
2. 由于负数在激进的前面，因此，\(-\sqrt{64}\)是\(−8\)，S\(−8\) ince 是一个实数，\(-\sqrt{64}\)是一个实数。

练习\(\PageIndex{17}\)

对于给定的每个数字，确定它是实数还是不是实数：

1. \(\sqrt{-196}\)
2. \(-\sqrt{81}\)

回答

1. 不是实数
2. 实数

练习\(\PageIndex{18}\)

对于给定的每个数字，确定它是实数还是不是实数：

1. \(-\sqrt{49}\)
2. \(\sqrt{-121}\)

回答

1. 实数
2. 不是实数

练习\(\PageIndex{19}\)

给定数字\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\)，列出

1. 整数
2. 整数
3. 有理数
4. 非理性数字
5. 实数

回答

1. 请记住，整数是 0、1、2、3... 而 8 是唯一给出的整数。
2. 整数是整数、它们的对立面和 0。 所以整数 8 是一个整数，而 −7 与整数相反，所以它也是一个整数。 另外，请注意，64 是 8 的平方，所以\(-\sqrt{64} = -8\)。 所以整数是\(−7, 8, \sqrt{64}\)。
3. 由于所有整数都是有理的，所以\(-7, 8, -\sqrt{64}\)都是有理的。 有理数还包括重复或停止的分数和小数，因此\(\frac{14}{5}\)\(5.9\)是有理的。 所以有理数的列表是\(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
4. 请记住，5 不是一个完美的正方形，所以\(\sqrt{5}\)是不合理的。
5. 列出的所有数字都是实数。

练习\(\PageIndex{20}\)

对于给定的数字，列出

1. 整数
2. 整数
3. 有理数
4. 非理性数字
5. 实数：\(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)

回答

1. \(4, \sqrt{49}\)。
2. \(−3, 4, \sqrt{49}\)
3. \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
4. \( -\sqrt{2}\)
5. \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)

练习\(\PageIndex{21}\)

对于给定的数字，列出

1. 整数
2. 整数
3. 有理数
4. 非理性数字
5. 实数：\(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

回答

1. \(6, \sqrt{121}\)。
2. \(−\sqrt{25}, −1, 6, \sqrt{121}\)
3. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
4. \(2.041975…\)
5. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

在数字行上找到分数

上次我们看数字线时，它上面只有正整数和负整数。 我们现在要在上面加入分数 s 和小数。

注意

进行操纵数学活动 “数字线第 3 部分” 将有助于你更好地了解分数在数字线上的位置。

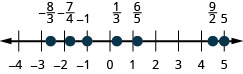
让我们从分数开始，在数字行\(\frac{8}{3}\)上找到\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\)和。

我们将从整数 3 和 −5 开始，因为它们最容易绘制。 参见图\(\PageIndex{4}\)。

列出的正确分数是\(\frac{1}{5}\text{ and } -\frac{4}{5}\)。 我们知道正确的分\(\frac{1}{5}\)数的值小于一，因此将位于 0 和 1 之间。 分母为 5，因此我们将从 0 到 1 的单位分成 5 个相等的部分\(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\)。 我们策划\(\frac{1}{5}\)。 参见图\(\PageIndex{4}\)。

同样，介\(-\frac{4}{5}\)于 0 和 −1 之间。 将单位分成 5 个相等的部分后，我们绘制图样\(-\frac{4}{5}\)。 参见图\(\PageIndex{4}\)。

最后，看看不正确的分数\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\)。 这些是分子大于分母的分数。 如果将每个点更改为混合数字，则定位这些点可能会更容易。 参见图\(\PageIndex{4}\)。

\[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]

该图\(\PageIndex{4}\)显示了绘制了所有点的数字线。

图\(\PageIndex{4}\)

练习\(\PageIndex{22}\)

在数字行上找到并标记以下内容：\(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\)和\(\frac{7}{3}\)。

回答

找到并绘制整数 4、−3。

\(\frac{3}{4}\)首先找到正确的分数。 分数介\(\frac{3}{4}\)于 0 和 1 之间。 将0和1之间的距离分成四个相等的部分，然后我们绘制图\(\frac{3}{4}\)。 同样的情节\(-\frac{1}{4}\)。

现在找到不正确的分数\(\frac{6}{5}\)\(-\frac{5}{2}\)，\(\frac{7}{3}\)。 如果我们将它们转换为混合数字，然后如上所述绘制它们，则绘制它们会更容易：\(\frac{6}{5} = 1\frac{1}{5}\)、\(-\frac{5}{2} = -2\frac{1}{2}\)、\(\frac{7}{3} = 2\frac{1}{3}\)。

练习\(\PageIndex{23}\)

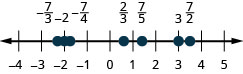
在数字行上找到并标记以下内容：\(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\)和\(-\frac{8}{3}\)。

回答

练习\(\PageIndex{24}\)

在数字行上找到并标记以下内容：\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\)和\(\frac{8}{3}\)。

回答

在练习中\(\PageIndex{25}\)，我们将使用不等式符号对分数进行排序。 在前面的章节中，我们使用数字行对号码进行排序。

• \(a < b\)当 a 位于数字行上 b 的左侧时，“a 小于 b”
• \(a > b\)当 a 位于数字行上 b 的右侧时，“a 大于 b”

当我们在数字线上从左向右移动时，数值会增加。

练习\(\PageIndex{25}\)

使用\(<\)或对以下每对数字进行排序\(>\)。 参考图可能会有所帮助\(\PageIndex{5}\)。

1. \(−\frac{2}{3}\text{___}-1\)
2. \(−3\frac{1}{2}\text{___}-3\)
3. \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
4. \(−2\text{___}-\frac{8}{3}\)

图\(\PageIndex{5}\)

回答

对负数进行排序时要小心。

1. \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
2. \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
3. \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
4. \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)

练习\(\PageIndex{26}\)

使用\(<\)或对以下每对数字进行排序\(>\)。

1. \(−\frac{1}{3}\text{___}-1\)
2. \(−1\frac{1}{2}\text{___}-2\)
3. \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
4. \(−3\text{___}-\frac{7}{3}\)

回答

1. \(>\)
2. \(>\)
3. \(<\)
4. \(<\)

练习\(\PageIndex{27}\)

使用\(<\)或对以下每对数字进行排序\(>\)。

1. \(−1\text{___}-\frac{2}{3}\)
2. \(−2\frac{1}{4}\text{___}-2\)
3. \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
4. \(−4\text{___}-\frac{10}{3}\)

回答

1. \(<\)
2. \(<\)
3. \(>\)
4. \(<\)

在数字行上找到小数

由于小数是分数的形式，因此在数字行上定位小数与在数字行上定位分数类似。

练习\(\PageIndex{28}\)

在数字行上找到 0.4。

回答

正确的分数的值小于一。 十进制数等\(0.4\)于\(\frac{4}{10}\)一个恰当的分数，因此位\(0.4\)于 0 和 1 之间。 在数字线上，将 0 和 1 之间的间隔分成 10 个相等的部分。 现在给零件贴上标签\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\)。 我们将 0 写成 0.0、1 和 1.0，这样数字就始终以十分之一为单位。 最后，在数字行\(0.4\)上标记。 参见图\(\PageIndex{6}\)。

图\(\PageIndex{6}\)

练习\(\PageIndex{29}\)

在数字行上找到：0.6。

回答

练习\(\PageIndex{30}\)

在数字行上找到：0.9。

回答

练习\(\PageIndex{31}\)

在数字行\(−0.74\)上找到。

回答

十进制 (−0.74\) 等效于\(-\frac{74}{100}\)，因此它位于 0 和 −1 之间。 在数字行上，标记并标出 0 到 −1 间隔内的百分位数。 参见图\(\PageIndex{7}\)。

图\(\PageIndex{7}\)

练习\(\PageIndex{32}\)

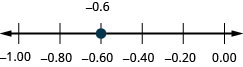
在数字行上找到：−0.6。

回答

练习\(\PageIndex{33}\)

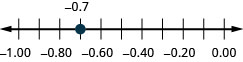
在数字行上找到：−0.7。

回答

哪个更大，0.04 还是 0.40？ 如果你把这看作是钱，你就知道0.40美元（四十美分）大于0.04美元（四美分）。 所以，\(0.40 > 0.04\)

同样，我们可以使用数字行对号码进行排序。

• \(a < b\)当 a 位于数字行上 b 的左侧时，“a 小于 b”
• \(a > b\)当 a 位于数字行上 b 的右侧时，“a 大于 b”

数字线上的 0.04 和 0.40 在哪里？ 参见图\(\PageIndex{8}\)。

图\(\PageIndex{8}\)

我们看到 0.40 在数字行上 0.04 的右边。 这是证明这一点的另一种方式\(0.40 > 0.04\)。

0.31 与 0.308 相比如何？ 这并不能转化为金钱以使其易于比较。 但是，如果我们将0.31和0.308转换为分数，我们可以分辨出哪个更大。

桌子\(\PageIndex{2}\)

	0.31	0.308
转换为分数。	\(\frac{31}{100}\)	\(\frac{308}{1000}\)
我们需要一个共同点来比较它们。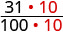
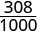	\(\frac{310}{1000}\)	\(\frac{308}{1000}\)

因为\(310 > 308\)，我们知道这一点\(\frac{310}{1000} > \frac{308}{1000}\)。 因此，\(0.31 > 0.308\)。

注意我们在转换\(0.31\)为分数时做了什么 — 我们从分数\(\frac{31}{100}\)开始，以等效分数结尾。\(\frac{310}{1000}\)转换\(\frac{310}{1000}\)回十进制得出 0.310。 因此，0.31 等于 0.310。 在十进制末尾写零不会改变其值！

\[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]

我们说 0.31 和 0.310 是等效的小数。

等效小数

如果两个小数转换为等效分数，则它们是等效的。

当我们排序小数时，我们使用等效的小数。

这里总结了我们对小数进行排序所采取的步骤。

对@@ 小数进行排序。

1. 将数字一个写在另一个之下，将小数点对齐。
2. 检查两个数字的位数是否相同。 如果不是，请在数字较少的末尾写零以使它们匹配。
3. 比较这些数字，就好像它们是整数一样。
4. 使用相应的不等式符号对数字进行排序。

练习\(\PageIndex{34}\)

\(0.64 \text{ ___ } 0.6\)使用\(<\)或订购\(>\)。

回答

\(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)

练习\(\PageIndex{35}\)

使用\(<\)或\(>\):对以下每对数字进行排序\(0.42 \text{ ___ } 0.4\)。

回答

\(>\)

练习\(\PageIndex{36}\)

使用\(<\)或\(>\):对以下每对数字进行排序\(0.18 \text{ ___ } 0.1\)。

回答

\(>\)

练习\(\PageIndex{37}\)

\(0.83 \text{ ___ } 0.803\)使用\(<\)或订购\(>\)。

回答

\(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)

练习\(\PageIndex{38}\)

使用\(<\)或\(>\):对以下每对数字进行排序\(0.76 \text{ ___ } 0.706\)。

回答

\(>\)

练习\(\PageIndex{39}\)

使用\(<\)或\(>\):对以下每对数字进行排序\(0.305 \text{ ___ } 0.35\)。

回答

\(<\)

当我们对负小数进行排序时，重要的是要记住如何对负整数进行排序。 回想一下，数字行的右边是较大的数字。 例如，因为 −2 位于数字行上 -3 的右边，所以我们知道这一点\(−2>−3\)。 同样，较小的数字位于数字行的左侧。 例如，因为 −9 位于数字行上 −6 的左边，所以我们知道这一点\(−9<−6\)。 参见图\(\PageIndex{9}\)。

图\(\PageIndex{9}\)

如果我们放大 0 和 −1 之间的间隔，如练习中所示\(\PageIndex{40}\)，我们将以相同的方式看到 an\(−0.2>−0.3\) d\(−0.9<−0.6\)。

练习\(\PageIndex{40}\)

使用\(<\)或\(>\)订购\(−0.1\text{ ___ }−0.8\)。

回答

\(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)

练习\(\PageIndex{41}\)

使用\(<\)或\(>\):订购以下一对数字\(−0.3\text{ ___ }−0.5\)。

回答

\(>\)

练习\(\PageIndex{42}\)

使用\(<\)或\(>\):订购以下一对数字\(−0.6\text{ ___ }−0.7\)。

回答

\(>\)

关键概念

• 平方根表示法
  \(\sqrt{m}\)读作 “的平方根”\(m\)。 如果\(m = n^{2}\)，那么\(\sqrt{m} = n\)，对于\(n \geq 0\)。
• 排序小数
  1. 将数字一个写在另一个之下，将小数点对齐。
  2. 检查两个数字的位数是否相同。 如果不是，请在数字较少的末尾写零以使它们匹配。
  3. 比较这些数字，就好像它们是整数一样。
  4. 使用相应的不等式符号对数字进行排序。

练习成就完美

使用平方根简化表达式

在以下练习中，进行简化。