7.4: 垂直线和水平线方程

Last updated
Save as PDF

Page ID: 171104

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

定义：垂直线

垂直线方程的形式为$x = c$，其中$c$是任何实数。垂直线将始终与该点处的$x$ −axis 相交$(c, 0)$。垂直线的斜率未定义。

示例 Template:Index

找到直线的斜率$x = 4$并绘制直线的图形。

解决方案

$x = 4$是一条垂直线的图形，如下图所示。

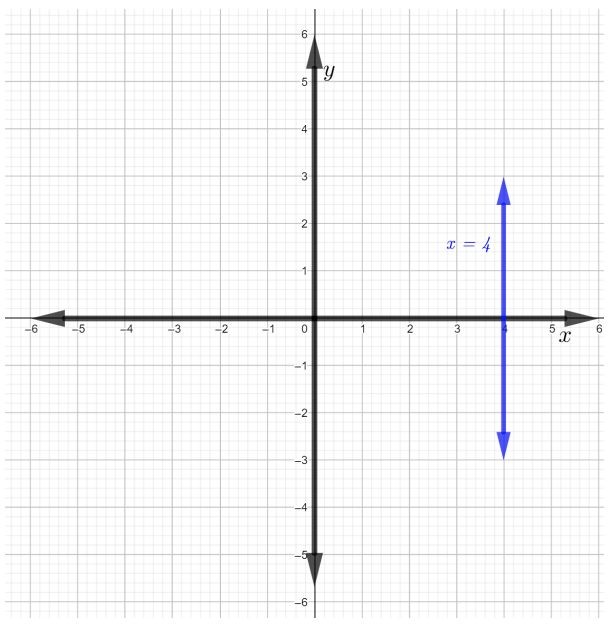
$clipboard_e96383c84992a62541d09b7ee1e53697f.png$

要找到直线的斜率，$x = 4$请选择直线上的任意两个不同点。让分数为 an$(4, −1)$ d$(4, 3)$。使用直线公式的斜率，

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3 − (−1)}{4 − 4} &\text{Substitute values} \\ &= \dfrac{4}{0} &\text{Simplify} \end{array}$

现在，如果$4$除以$0$，这相当于问一个问题：“零乘以多$4$少？” 答案是，没有这样的数字。除以零是未定义的，垂直线的斜率$x = 4$未定义。

定义：水平线

水平线方程的形式为$y = k$，其中$k$是任何实数。水平线将始终与该点处的$y$ −axis 相交$(0, k)$。水平线的斜率为零。

示例 Template:Index

找出穿过点的直线的斜率，$(−3, −2)$然后$(4, −2)$。绘制点并绘制穿过它们的线条的图形。

解决方案

使用直线公式的斜率。因此，

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{(−2) − (−2)}{4 − (−3)} &\text{Substitute values} \\ &= \dfrac{0}{7} &\text{Simplify} \\ &= 0 &\text{\(0$除以任何非零数等于零}\ end {array}\)

因此，穿过两个给定点的直线是一条水平线，斜率等于零，如下图所示。

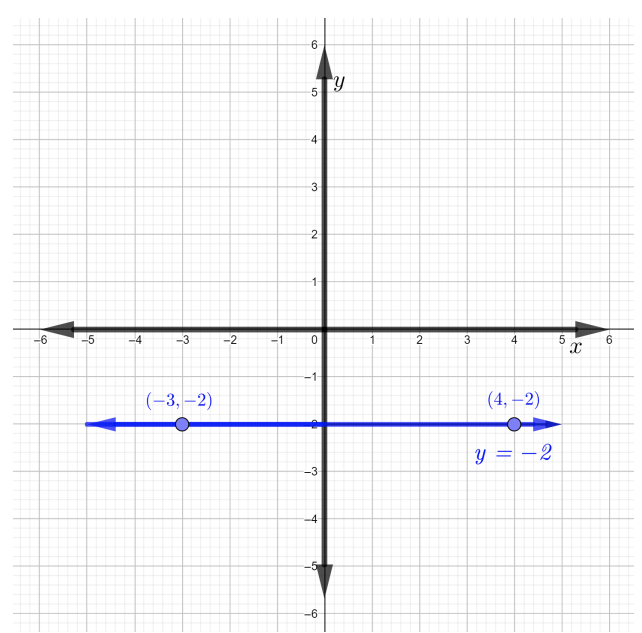
$clipboard_e08cf4386944def611c6831ac921a6f6d.png$

示例 Template:Index

绘制直线图$y − 3 = 0$并找出其斜率。

解决方案

这行$y − 3 = 0$可以写成$y = 3$（加$3$到等式的两边）。这条线$y = 3$是一条水平线，如下图所示。

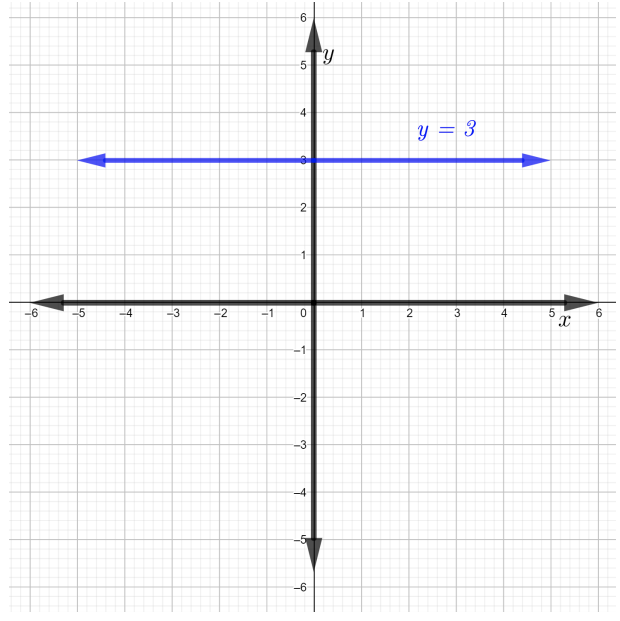
$clipboard_ef5d1c3aa2712f38f53b81ce34e7a1ee0.png$

现在，要找到斜率，请在直线上选择任意两个不同的点$y = 3$。考虑积分$(0, 3)$和$(3, 3)$. 因此，

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{The slope of a line formula} \\ &= \dfrac{3-3}{3-0} &\text{Substitute values} \\ &= \dfrac{0}{2} &\text{Simplify} \\ &= 0 &\text{\(0$除以任何非零数等于零}\ end {array}\)

因此，给定线的斜率为$m = 0.$

练习 Template:Index

找出每条线的斜率。

$x = −\dfrac{1}{2}$
$y − 1 = 0$
$x + 7 = 10$
$y + 2 = −9$
找出穿过点的直线的斜率，$(−4, 1)$然后$(2, 1)$。绘制点并绘制穿过它们的线条的图形。
找出穿过点的直线的斜率，$(−3, 5)$然后$(−3, −7)$。绘制点并绘制穿过它们的线条的图形。