Skip to main content
Global

7.5: 直线方程的形式

  1. Last updated
  2. Save as PDF
  • Page ID
    171123

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    上一节解释了垂直线和水平线的方程。 现在发现直线方程的另外三种形式，即斜率截距形式、点斜率形式和标准形式。

    直线方程的斜率截距形式

    定义：斜率截距形式

    直线方程的斜率截距形式为：

    \[y = mx + b \nonumber \]

    其中\(m\)是直线的斜率，\((0, b)\)是\(y\) −截距。

    请注意，\(y\)-intercept 是直线与\(y\) −axis 相交的点，也就是时间\(x = 0\)。

    示例 Template:Index

    用给定的斜率和\(y\)截距写一个直线方程。

    1. 斜率 =\(5\);\(y\) −截距\((0, \dfrac{1}{2})\)
    2. 斜率 =\(−\dfrac{5}{6}\);\(y\) − 截距\((0, −\dfrac{3}{4})\)

    解决方案

    1. \(m = 5\)和\(b = \dfrac{1}{2}\)

    直线的方程为 for\(y = mx + b\)。 因此，

    \(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= 5x + \dfrac{1}{2} &\text{Substitute \(m = 5\)和\(b = \dfrac{1}{2}\)}\ end {array}\)

    因此，\(y = 5x + \dfrac{1}{2}\)是具有给定斜率和\(y\)-截距的直线的方程。

    1. Given\(m = −\dfrac{5}{6}\) and\(b = −\dfrac{3}{4}\)

    因此，

    \(\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= −\dfrac{5}{6}x −\dfrac{3}{4} &\text{Substitute values} \end{array}\)

    因此，\(y = −\dfrac{5}{6}x − \dfrac{3}{4}\)是具有给定斜率和\(y\)-截距的直线的方程。

    示例 Template:Index

    然后确定斜率和\(y\) −截距，用它们绘制每条线的图形。

    1. \(y = −2x + 4\)
    2. \(5y − 3x = 10\)

    解决方案

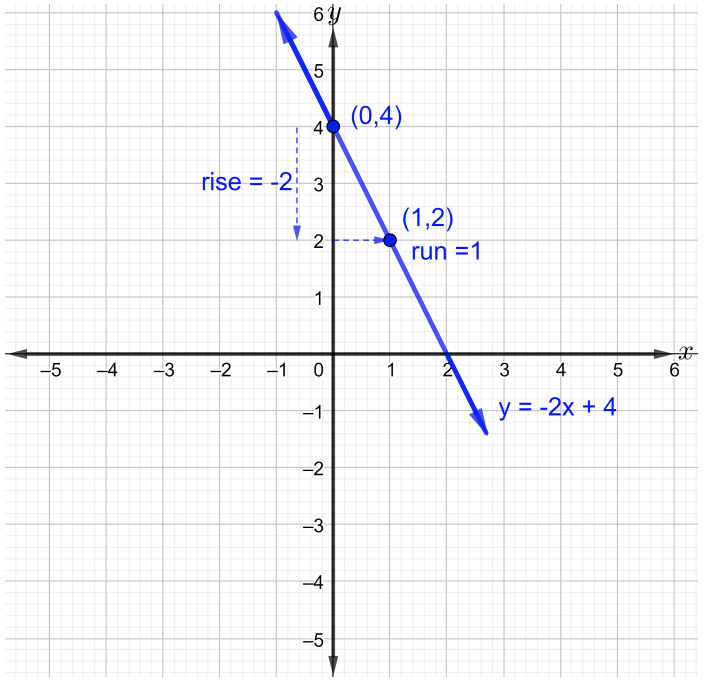
    a. 请注意，给定的线性方程采用斜率截距形式。 所以，\(m = −2\)或者等同地\(m = −\dfrac{2}{1}\)，还有\(b = 4\)

    \(m\)那就是直线的斜率\(m = \dfrac{\text{rise}}{\text{run}} = −\dfrac{2}{1}\)。 要绘制直线图，请至少绘制两个点。 从\(y\) −intercep\((0, 4)\) t 开始，向下移动\(2\)单位，然后向右\(1\)移动以绘制第二个点。 现在，用一条直线连接这两个点，如下图所示。

    clipboard_e5fcc0c548a6809df50a713b48295362a.png

    b. 请注意，尚不清楚如何识别给定线性方程中的斜率和\(y\)截距，因为它不是斜率截距形式。 因此，\(y\)求解方程采用斜率截距形式，如下所示，

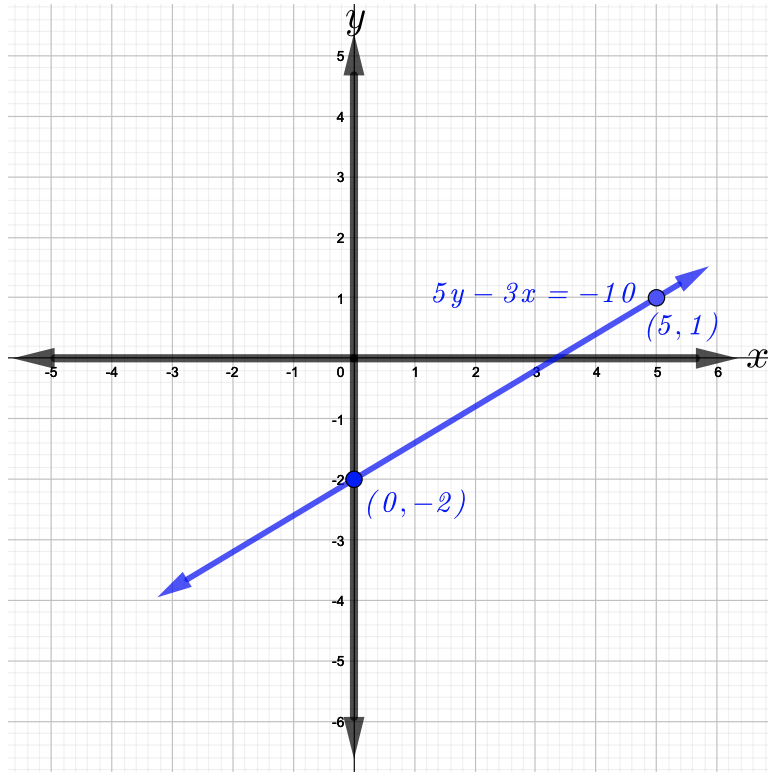
    \(\begin{array} &&5y − 3x = −10 &\text{Given} \\ &5y = 3x − 10 &\text{Add \(3x\)到方程的两边}\\ &y =\ dfrac {3} {5} x − 2 &\ text {将所有项除\(5\)以隔离\(y\)}\ end {array}\)

    现在，还\(m = \dfrac{3}{5}\)有\(b = −2\)。 首先绘制\(y\)-intercept，\((0, −2)\)然后向上移动\(3\)\(5\)单位，向右移动单位，然后绘制第二个点，即\((5, 1)\)。 现在，将这两个点连接起来，即\((5, 1)\)，\((0, −2)\)和，得到下图所示的直线图。

    clipboard_eca3205bebd002556f4570dc0193cd9f6.png

    练习 Template:Index

    用给定的斜率和\(y\)截距写一个直线方程。

    1. 斜率：\(2\)\(y\)-截距：\((0, \dfrac{3}{4})\)
    2. 斜率：\(\dfrac{5}{7}\)\(y\)-截距：\((0, −6)\)
    3. 斜率：\(−\dfrac{1}{2}\)\(y\)-截距：\((0, −\dfrac{7}{11} )\)
    练习 Template:Index

    识别斜率和\(y\)截距，然后使用它们绘制每条线的图形。

    1. \(y = 5x − 3\)
    2. \(2y = −6x + 1\)

    直线方程的点斜率形式

    定义：点-斜率形式

    直线方程的点斜率形式为：

    \[y − y_1 = m(x − x_1) \nonumber \]

    哪里\(m\)是直线的斜率，\((x_1, y_1)\)是直线上的任何点。

    示例 Template:Index

    求出穿过给定点和给定斜率的每条线的方程。

    1. 斜率\(3\)和点\((−1, 8)\)
    2. 斜率\(−\dfrac{5}{2}\)和点\((\dfrac{4}{3}, \dfrac{1}{3})\)

    解决方案

    1. 要找到穿过\((−1, 8)\)带斜率点的直线的方程\(m = 3\)，请使用点斜率形式，如下所示：

    \(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 8 = 3[x − (−1)] &\text{Substitute \(m = 3\)\(x_1 = −1\), 和\(y_1 = 8\)}\\ &y − 8 = 3 (x + 1) &\ text {Simplify}\\ &y − 8 = 3x + 3 &\ text {方程右侧的两个项乘以\(3\)}\\ &y = 3x + 11 &\ text {\(8\)添加到等值的两边以隔离\(y\)}\ end {array}\)

    因此，\(y = 3x + 11\)是具有给定斜率和点的直线的方程。 这条线采用斜率截距形式。

    1. 与 a 部分类似，使用点斜率表单，如下所示：

    \(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ & y−(−\dfrac{1}{3}) = −\dfrac{5}{2} (x −\dfrac{4}{3}) &\text{Substitute \(m = −\dfrac{5}{2},\;\; x_1 = \dfrac{4}{3}\)，还有\(y_1 = −\dfrac{1}{3}\)}\\ &y +\ dfrac {1} {3} = −\ dfrac {5} {2} x +\ dfrac {20} {6} &\ text {分发和简化}\\ &y = −\ dfrac {5} {2} x +\ dfrac {20} {6} −\ dfrac {1} {3}\(\dfrac{1}{3}\) 来自两边}\\ &y = −\ dfrac {5} {2} x + 3 &\ text {要合并这两个分数，请注意液晶屏\(= 6\)。}\\ &\ text {将分子和分母乘以\(\dfrac{1}{3}\) y\(2\) 然后简化:}\\ & &\ tex\(\dfrac{20}{6} − \dfrac{1(2)}{3(2)} = \dfrac{20}{6} − \dfrac{2}{6} = \dfrac{18}{6} = 3\) t {}\ end {array}\)

    因此，\(y = −\dfrac{5}{2}x + 3\)是穿过给定点和给定斜率的直线的方程。

    示例 Template:Index

    找出给定点\((2, 4)\)和直线的方程\((−3, 9)\)。

    请注意，本章前面已经解释了如何在给定斜率和\(y\)截距的情况下找到直线的方程。 本章还解释了如何在给定直线上的任何点和斜率的情况下找到直线的方程。 因此，在这两种方法中，斜率都是给出的。

    解决方案

    要在给定直线上任意两点的情况下找到直线的方程，首先使用直线公式的斜率求出斜率。 之后，对任意给定点应用点斜率表单。 首先，使用这两个点来找出直线的斜率。 让我们\((x_1, y_1) = (2, 4)\)和\((x_2, y_2) = (−3, 9)\)。 然后，

    \(\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Slope of the line formula} \\ &= \dfrac{9 − 4}{−3 − 2} &\text{Substitute values} \\ &= \dfrac{5}{−5} &\text{Simplify} \\ &= −1 & \end{array}\)

    现在已经找到了斜率，接下来使用任何一个给定点来找出直线的方程。 因此\(m = −1\)，可以考虑使用积分\((2, 4)\)。

    \(\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-slope form} \\ &y − 4 = −1(x − 2) &\text{Substitute \(m = −1\),\(x_1 = 2\),\(y_1 = 4\)}\\ &y − 4 = −x + 2 &\ text {分布\(-1\)到右边的两个项}\\ &y = −x + 6 &\ text {\(4\)添加到方程的两边以隔离\(y\)}\ end {array}\)

    因此，\(y = −x + 6\)是穿过给定点的直线的方程，具有斜率截距形式。

    练习 Template:Index

    求出每条穿过给定点并具有给定斜率的直线的方程。

    1. 斜率\(−\dfrac{5}{2}\)和点\((3, 0)\)。
    2. 斜率\(\dfrac{1}{2}\)和点\((−2, −3)\)。
    练习 Template:Index

    给定以下点，找出直线的方程。

    1. \((−9, −3)\)和\((6, −2)\)
    2. \((4, 1)\)和\((−2, 2)\)

    直线方程的标准形式（又名线性方程的通用形式）

    定义：标准表单

    非垂直线的标准形式为

    \[Ax + By = C \nonumber \]

    其中\(A\)是正整数\(B\)，\(C\)是带的整数\(B \neq 0\)。

    示例 Template:Index

    绘制以下方程的每一行：

    1. \(4x − 3y = 6\)
    2. \(\dfrac{1}{2} − y + 1 = 0\)

    请注意，\(x\)-intercept 是直线与\(x\)-axis 相交的点。 也就是说，什么时候\(y = 0\)。 因此，\(x\)-intercept 是形式上的一个点\((a, 0)\)，其中\(a\)是任何实数。

    解决方案

    1. 方程\(4x − 3y = 6\)为标准形式。 要绘制给定方程的线条，可以使用多种方法。 例如，求解得到斜率截距形式的方程，然后绘制直线图。\(y\) 也可以找到两个点，然后绘制线条图。 最容易快速找到的两个点是\(x\)和\(y\)截取。 因此，建议使用此方法。

    要找到\(x\)-intercept，请\(y = 0\)在给定方程中设置并求解，\(x\)如下所示，

    \(\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4x − 3(0) = 6 &\text{Substitute \(y = 0\)}\\ &4x = 6 &\ text {Simplify}\\ &x =\ dfrac {6} {4} &\ text {除以方程的\(4\)两边}\\ &x =\ dfrac {3} {2} &\ text {Simplify}\ end {array}\)

    因此，\(x\)-intercept 就是重点\((\dfrac{3}{2}, 0)\)

    现在，要找到\(y\)-intercept，请设置\(x = 0\)如下，

    \(\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4(0) − 3y = 6 &\text{Substitute \(x = 0\)}\\ &−3y = 6 &\ text {Simplify}\\ &y = 6 −3 &\ text {除以方程的\(−3\)两边}\\ &y = −2 &\ text {Simplify}\ end {array}\)

    现在，绘制这些点\((\dfrac{3}{2}, 0)\)\((0, −2)\)并绘制穿过它们的直线图，如下图所示。

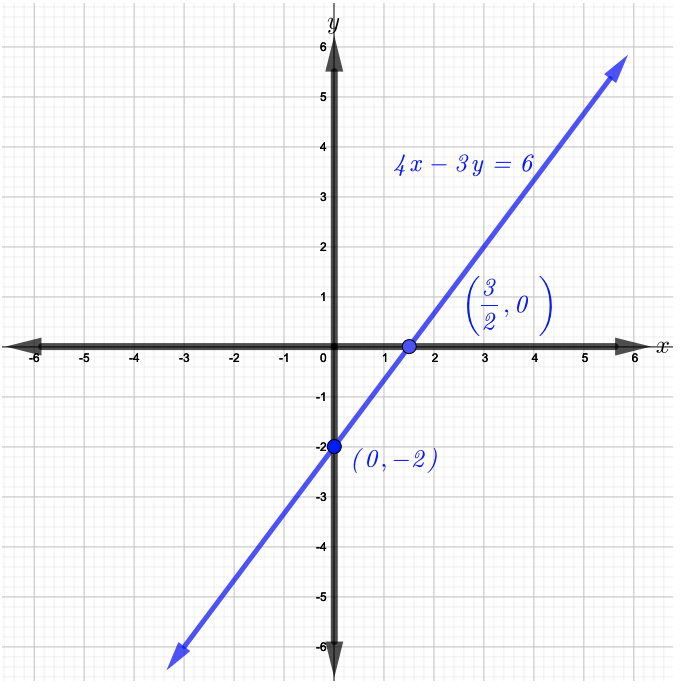
    clipboard_ede795f89eb03e5b448b62ec8dc0b7663.png

    该方程\(\dfrac{1}{2} x − y + 1 = 0\)不是标准形式。 因此，\(1\)从方程的两边减去现在\(\dfrac{1}{2}x − y = −1\)是标准形式的。

    同样，与 b 部分类似，找到 and\(y\)-\(x\) intercepts。 首先，通过设置找到\(x\)-intercept，\(y = 0\)然后按\(x\)如下方式求解。

    \( \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}x − (0) = −1 &\text{Substitute \(y = 0\)}\\ &\ dfrac {1} {2} x = −1 &\ text {Simplify}\\ &x = −2 &\ text {乘以方程的\(2\)两边。} \ end {array}\)

    因此，\(x\)-截距是重点\((−2, 0)\)。

    现在，设置\(x = 0\)为查找\(y\)-intercept，如下所示：

    \( \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}(0) − y = −1 &\text{Substitute \(x = 0\)}\\ &−y = −1 &\ text {Simplify}\\ &y = 1 &\ text {乘以\(-1\)。} \ end {array}\)

    因此，\(y\)-截距为\((0, 1)\)。

    绘制\(x\)和\(y\)-intercepts\((0, 1)\)，\((−2, 0)\)然后绘制穿过它们的直线图，如下图所示。

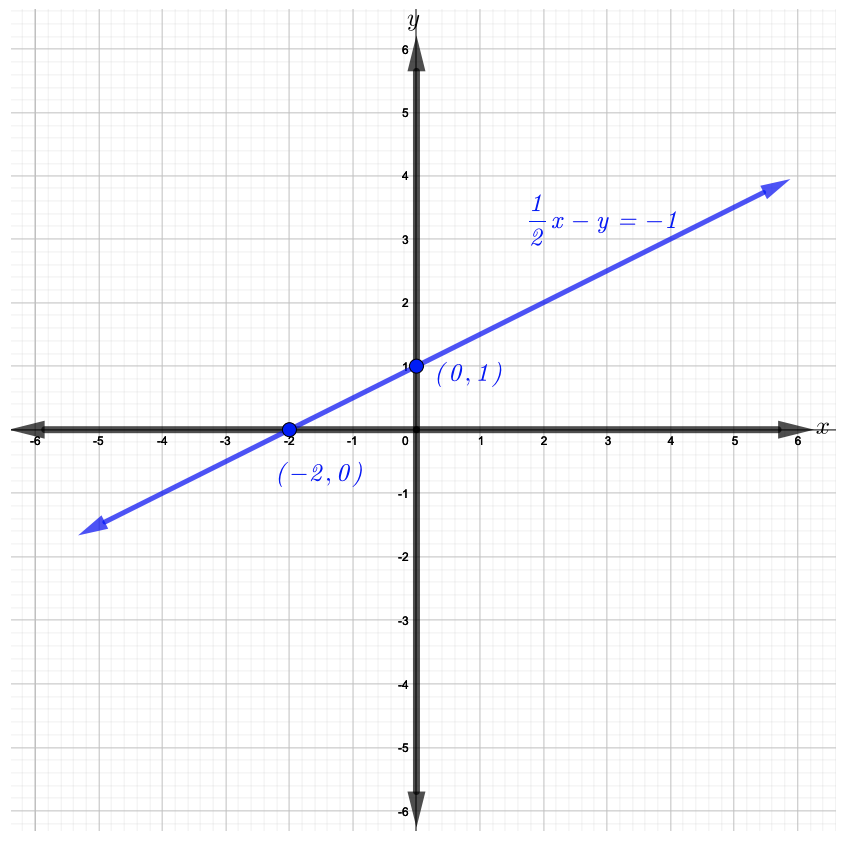
    clipboard_e3475016017c80b2298d3517f4bef3bf0.png

    本节没有作业。