11.3E:练习
- Page ID
- 204354
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
练习成就完美
在以下练习中,使用属性绘制每个方程的图表。
- \(y=-x^{2}+4 x-3\)
- \(y=-x^{2}+8 x-15\)
- \(y=6 x^{2}+2 x-1\)
- \(y=8 x^{2}-10 x+3\)
- 回答
-
1。
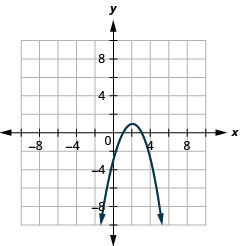
图 11.2.83 3。
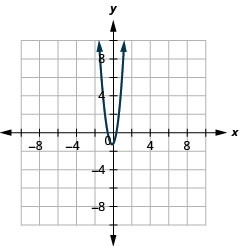
图 11.2.84
在以下练习中,
- 用标准形式写下方程式然后
- 使用标准形式的属性绘制方程图。
- \(y=-x^{2}+2 x-4\)
- \(y=2 x^{2}+4 x+6\)
- \(y=-2 x^{2}-4 x-5\)
- \(y=3 x^{2}-12 x+7\)
- 回答
-
1。
- \(y=-(x-1)^{2}-3\)
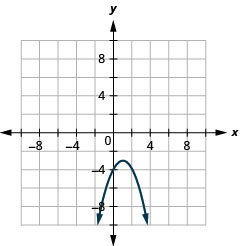
图 11.2.85 3。
- \(y=-2(x+1)^{2}-3\)
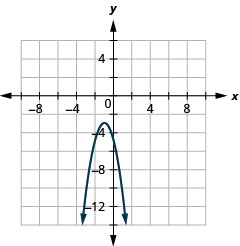
图 11.2.86
在以下练习中,使用属性绘制每个方程的图表。
- \(x=-2 y^{2}\)
- \(x=3 y^{2}\)
- \(x=4 y^{2}\)
- \(x=-4 y^{2}\)
- \(x=-y^{2}-2 y+3\)
- \(x=-y^{2}-4 y+5\)
- \(x=y^{2}+6 y+8\)
- \(x=y^{2}-4 y-12\)
- \(x=(y-2)^{2}+3\)
- \(x=(y-1)^{2}+4\)
- \(x=-(y-1)^{2}+2\)
- \(x=-(y-4)^{2}+3\)
- \(x=(y+2)^{2}+1\)
- \(x=(y+1)^{2}+2\)
- \(x=-(y+3)^{2}+2\)
- \(x=-(y+4)^{2}+3\)
- \(x=-3(y-2)^{2}+3\)
- \(x=-2(y-1)^{2}+2\)
- \(x=4(y+1)^{2}-4\)
- \(x=2(y+4)^{2}-2\)
- 回答
-
1。
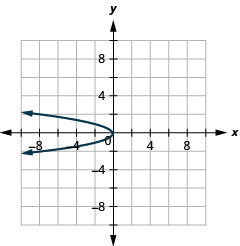
图 11.2.87 3。
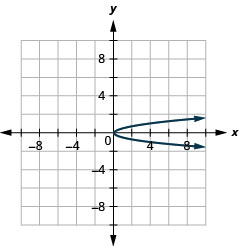
图 11.2.88 5。
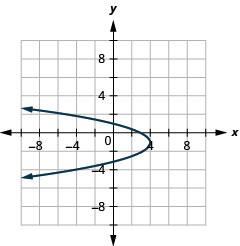
图 11.2.89 7。
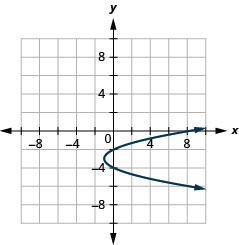
图 11.2.90 9。
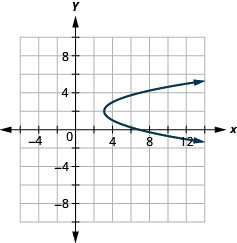
图 11.2.91 11。
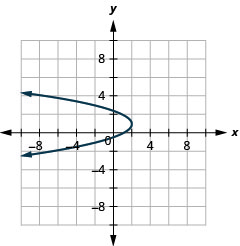
图 11.2.92 13。
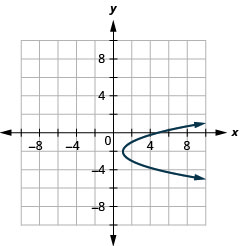
图 11.2.93 15。
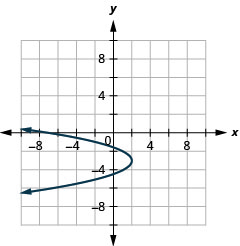
图 11.2.94 17。
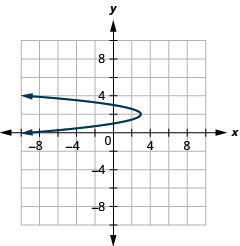
图 11.2.95 19。
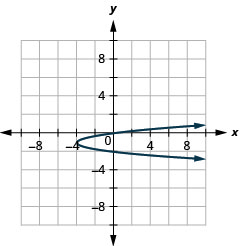
图 11.2.96
在以下练习中,
- 用标准形式写下方程式然后
- 使用标准形式的属性绘制方程图。
- \(x=y^{2}+4 y-5\)
- \(x=y^{2}+2 y-3\)
- \(x=-2 y^{2}-12 y-16\)
- \(x=-3 y^{2}-6 y-5\)
- 回答
-
1。
- \(x=(y+2)^{2}-9\)
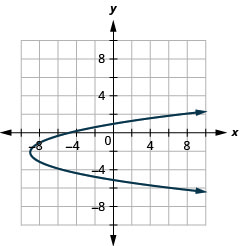
图 11.2.97 3。
- \(x=-2(y+3)^{2}+2\)
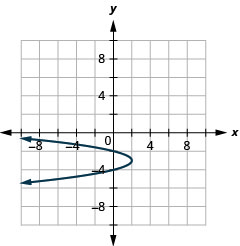
图 11.2.98
在以下练习中,将每张图表与以下方程之一进行匹配:
- \(x^{2}+y^{2}=64\)
- \(x^{2}+y^{2}=49\)
- \((x+5)^{2}+(y+2)^{2}=4\)
- \((x-2)^{2}+(y-3)^{2}=9\)
- \(y=-x^{2}+8 x-15\)
- \(y=6 x^{2}+2 x-1\)
1。
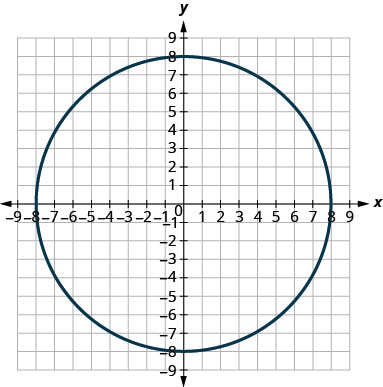
2。
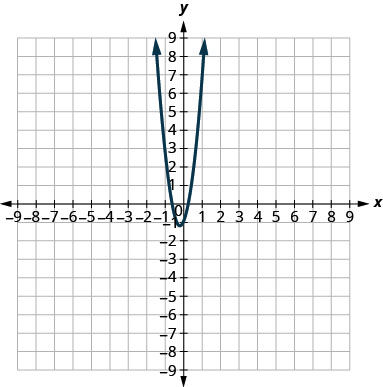
3。
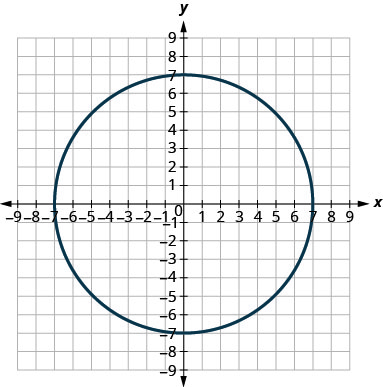
4。
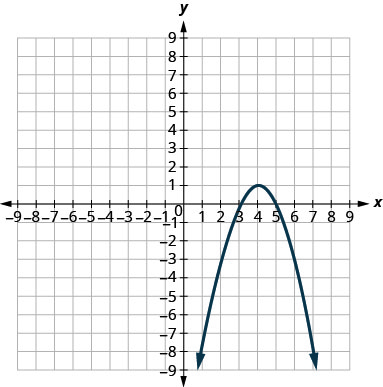
5。
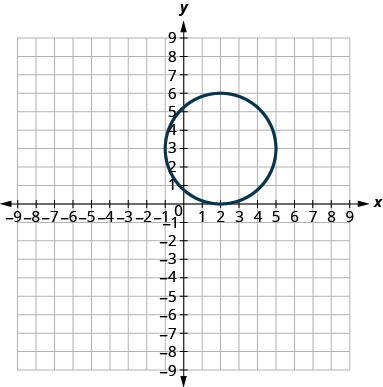
6。
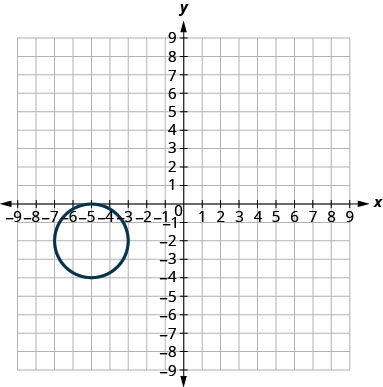
- 回答
-
1. 一个
3. b
5. d
用所示桥基上形成的抛物线拱的标准形式写下方程。 使用桥的左下角作为原点\((0, 0)\)。
1。
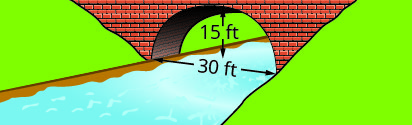
2。
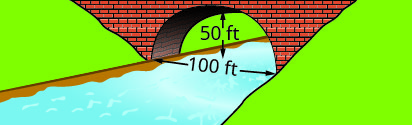
3。
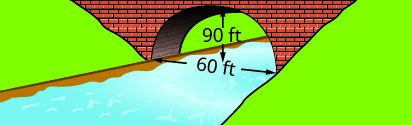
4。
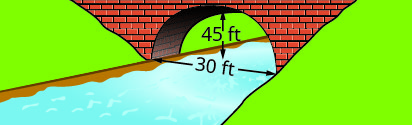
- 回答
-
1。 \(y=-\frac{1}{15}(x-15)^{2}+15\)
3。 \(y=-\frac{1}{10}(x-30)^{2}+90\)
- 用你自己的话说,定义一个抛物线。
- 抛物线\(y=x^{2}\)是一种函数吗? 抛物线\(x=y^{2}\)是一种函数吗? 解释原因或原因。
- 写下以标准形式向上或向下打开的抛物线的方程式和以标准形式向左或向右打开的抛物线的方程式。 为每个抛物线提供草图,标注对称的顶点和轴。
- 用你自己的话解释一下,如何从它的方程式中分辨出抛物线是向上、向下、向左还是向右打开。
- 回答
-
1。 答案可能有所不同
3。 答案可能有所不同
自检
a. 完成练习后,使用此清单评估您对本节目标的掌握程度。
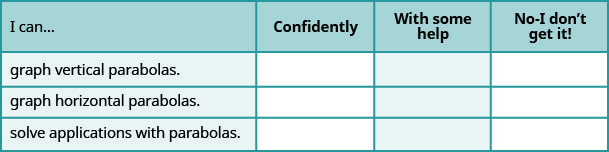
b. 看完这份清单后,你会怎么做才能对所有目标充满信心?


