11.3: 抛物线
- Page ID
- 204339
在本节结束时,您将能够:
- 绘制垂直抛物线
- 绘制水平抛物线
- 使用抛物线求解应用程序
在开始之前,请参加这个准备测验。
- 图:\(y=-3 x^{2}+12 x-12\)。
如果您错过了此问题,请查看示例 9.47。 - 通过完成方块求解:\(x^{2}-6 x+6=0\).
如果您错过了此问题,请查看示例 9.12。 - 以标准形式写入:\(y=3 x^{2}-6 x+5\).
如果您错过了此问题,请查看示例 9.59。
绘制垂直抛物线
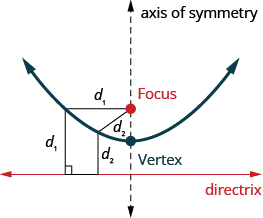
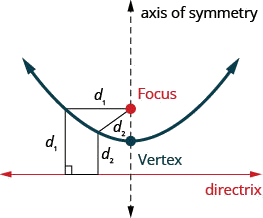
我们要看的下一个圆锥部分是抛物线。 我们将抛物线定义为平面中与定点和固定线距离相同的所有点。 定点称为焦点,固定线称为抛物线的直线。
抛物线是平面中与定点和固定线距离相同的所有点。 定点称为焦点,固定线称为抛物线的直线。
以前,我们学会了使用属性从通用形式或标准形式绘制垂直抛物线图。 这些方法在这里也将起作用。 我们将在这里总结这些属性。
垂直抛物线
|
通用表格 \(y=a x^{2}+b x+c\) |
标准表单 \(y=a(x-h)^{2}+k\) |
|
|---|---|---|
| 方向 | \ (y=a x^ {2} +b x+c\)” >\(a>0\) 向上;\(a<0\)向下 | \ (y=a (x-h) ^ {2} +k\)” >\(a>0\) 向上;\(a<0\)向下 |
| 对称轴 | \ (y=a x^ {2} +b x+c\)” >\(x=-\dfrac{b}{2 a}\) | \ (y=a (x-h) ^ {2} +k\)” >\(x=h\) |
| 顶点 | \ (y=a x^ {2} +b x+c\)” >替换\(x=-\dfrac{b}{2 a}\)并 求解\(y .\) |
\ (y=a (x-h) ^ {2} +k\)” >\((h, k)\) |
| \(y\)-截距 | \ (y=a x^ {2} +b x+c\)” >Let\(x=0\) | \ (y=a (x-h) ^ {2} +k\)” >Let\(x=0\) |
| \(x\)-拦截 | \ (y=a x^ {2} +b x+c\)” >Let\(y=0\) | \ (y=a (x-h) ^ {2} +k\)” >Let\(y=0\) |
这些图表显示了抛物线向上或向下打开时的样子。 它们相对于\(y\)-或\(x\)-轴的位置只是一个例子。
为了从这些表单中绘制抛物线,我们使用了以下步骤。
如何绘制垂直抛物线图\(y=a x^{2}+b x+c\)或\(f(x)=a(x-h)^{2}+k\)使用属性。
- 第 1 步:确定抛物线是向上还是向下打开。
- 第 2 步。 找到对称轴。
- 第 3 步。 找到顶点。
- 第 4 步。 找到\(y\)截距。 在对称轴上找到\(y\)与-截距对称的点。
- 第 5 步。 找到\(x\)-截图。
- 第 6 步。 绘制抛物线图。
下一个示例回顾了根据抛物线方程的一般形式绘制抛物线的方法。
使用属性绘\(y=-x^{2}+6 x-8\)制图表。
解决方案:
| \( \begin{align*} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt] \color{black}{y} &=-x^{2}+6 x-8 \end{align*}\) | |
| \(a\)既然\(-1\)如此,抛物线向下打开。 | |
 |
|
| 要找到对称轴,请找到\(x=-\dfrac{b}{2 a}\)。 | \( \begin{align*} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align*}\) |
| 对称轴是\(x=3\)。 | |
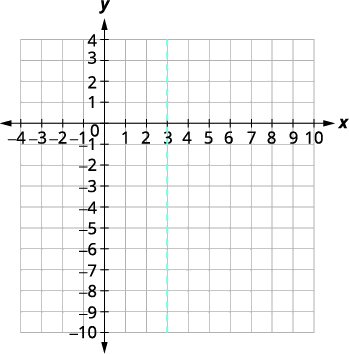 |
|
| 顶点在线上\(x=3\)。 | \(y=-x^{2}+6 x-8\) |
| 让\(x=3\)。 | 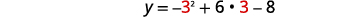 |
| \(\begin{align*} y &=-9+18-8 \\[4pt] y &=1 \end{align*}\) | |
| 顶点是\((3,1)\)。 | |
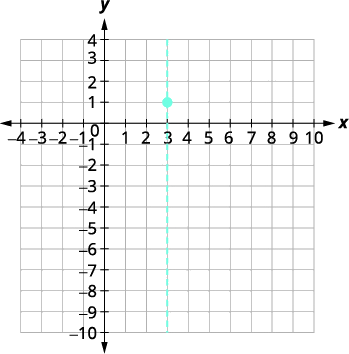 |
|
| \(y\)-截距发生在\(x=0\). | \(y=-x^{2}+6 x-8\) |
| 替代\(x=0\)。 | \(y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8\) |
| 简化。 | \(y=-8\) |
| \(y\)-截距为\((0,-8)\)。 | |
| 该点\((0,−8)\)位于对称线左侧的三个单位。 对称线右边三个单位的点是\((6,−8)\)。 | 与\(y\)-截距对称的点是\((6,−8)\)。 |
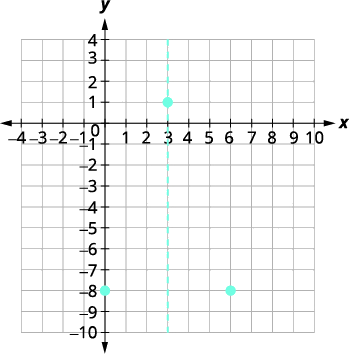 |
|
| \(x\)-截距发生在\(y=0\). | \(y=-x^{2}+6 x-8\) |
| 让\(y=0\)。 | \(\color{red}{0} \color{black}{=}-x^{2}+6 x-8\) |
| 将全球公积金考虑在内。 | \(0=-\left(x^{2}-6 x+8\right)\) |
| 将三项式分解为因子。 | \(0=-(x-4)(x-2)\) |
| 求解\(x\)。 | \(x=4, \quad x=2\) |
| \(x\)-intercepts 是\((4,0),(2,0)\)。 | |
| 绘制抛物线图。 | 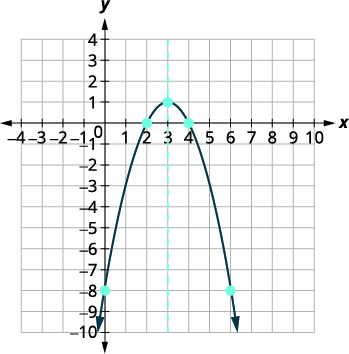 |
使用属性绘\(y=-x^{2}+5 x-6\)制图表。
- 回答
-
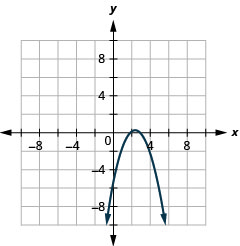
图 11.2.24
使用属性绘\(y=-x^{2}+8 x-12\)制图表。
- 回答
-
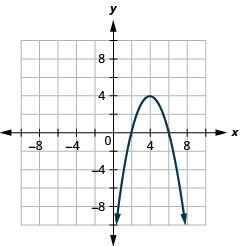
图 11.2.25
下一个示例回顾了根据其方程的标准形式绘制抛物线的方法\(y=a(x-h)^{2}+k\)。
\(y=3 x^{2}-6 x+5\)以标准形式书写,然后使用标准形式的属性绘制方程图。
解决方案:
| 通过填写方块来重写\(y=a(x-h)^{2}+k\)表单中的函数。 | \(\begin{align*} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3 \\[4pt] y &=3(x-1)^{2}+2 \end{align*}\) |
| 识别常量\(a, h, k\)。 | \(a=3, h=1, k=2\) |
| 因为\(a=2\),抛物线向上打开。 | |
 |
|
| 对称轴是\(x=h\)。 | 对称轴是\(x=1\)。 |
| 顶点是\((h,k)\)。 | 顶点是\((1,2)\)。 |
| 通过替换找到\(y\)-截距\(x=0\), | \( \begin{align*} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align*} \) |
| \(y\)-截距\((0,5)\) | |
| 找到与对称轴\((0,5)\)对称的点。 | \((2,5)\) |
| 找到\(x\)-截图。 | \(\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}\) |
| 负数的平方根告诉我们解是复数。 所以没有\(x\)-intercepts。 | |
| 绘制抛物线图。 | 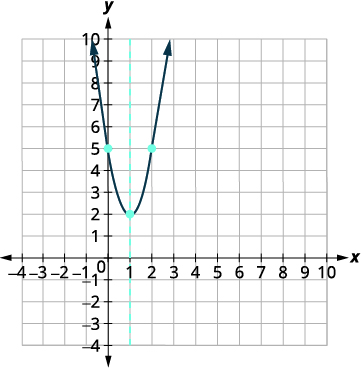 |
- \(y=2 x^{2}+4 x+5\)以标准形式书写然后
- 使用标准形式的属性来绘制方程式。
- 回答
-
- \(y=2(x+1)^{2}+3\)
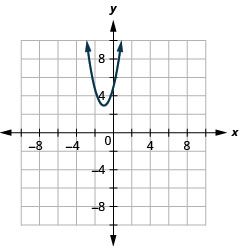
图 11.2.28
- \(y=-2 x^{2}+8 x-7\)以标准形式书写然后
- 使用标准形式的属性来绘制方程式。
- 回答
-
- \(y=-2(x-2)^{2}+1\)
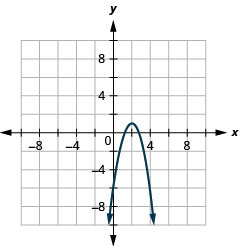
图 11.2.29
绘制水平抛物线
到目前为止,我们的工作只涉及向上或向下打开的抛物线。 我们现在要看水平抛物线。 这些抛物线要么向左打开,要么向右打开。 如果我们在之前的方程\(y\)中将\(x\)和互换为抛物线,则会得到向左或向右打开的抛物线的方程。
水平抛物线
|
通用表格 \(x=a y^{2}+b y+c\) |
标准表单 \(x=a(y-k)^{2}+h\) |
|
|---|---|---|
| 方向 | \ (x=a y^ {2} +b y+c\) “>\(a>0\) 右;\(a<0\)左 | \ (x=a (y-k) ^ {2} +h\) “>\(a>0\) 右;\(a<0\)左 |
| 对称轴 | \ (x=a y^ {2} +b y+c\)” >\(y=-\dfrac{b}{2 a}\) | \ (x=a (y-k) ^ {2} +h\)” >\(y=k\) |
| 顶点 | \ (x=a y^ {2} +b y+c\)” >替换\(y=-\dfrac{b}{2 a}\)并 求解\(x .\) |
\ (x=a (y-k) ^ {2} +h\)” >\((h, k)\) |
| \(x\)-拦截 | \ (x=a y^ {2} +b y+c\)” >Let\(x=0\) | \ (x=a (y-k) ^ {2} +h\)” >Let\(x=0\) |
| \(y\)-截距 | \ (x=a y^ {2} +b y+c\)” >Let\(y=0\) | \ (x=a (y-k) ^ {2} +h\)” >Let\(y=0\) |
这些图表显示了抛物线向左或向右时的样子。 它们相对于\(y\)-或\(x\)-轴的位置只是一个例子。
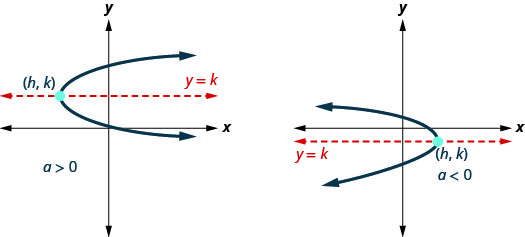
看看这些抛物线,它们的图表代表一个函数吗? 由于两张图都无法通过垂直线测试,因此它们不代表函数。
绘制向左或向右打开的抛物线基本上与我们对向上或向下打开的抛物线所做的相同,但\(x\)和\(y\)变量反转。
- 第 1 步:确定抛物线是向左还是向右打开。
- 步骤 2:找到对称轴。
- 步骤 3:找到顶点。
- 第 4 步:找到\(x\)截距。 在对称轴上找到\(x\)与-截距对称的点。
- 第 5 步:找到\(y\)-intercepts。
- 第 6 步:绘制抛物线图。
使用属性绘\(x=2 y^{2}\)制图表。
解决方案:
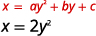 |
|
| 因为\(a=2\),抛物线向右打开。 | |
 |
|
| 要找到对称轴,请找到\(y=-\dfrac{b}{2 a}\) | \(y=-\dfrac{b}{2 a}\) |
| \(y=-\dfrac{0}{2(2)}\) | |
| \(y=0\) | |
| 对称轴是\(y=0\)。 | |
| 顶点在线上\(y=0\)。 | \(x=2 y^{2}\) |
| 让\(y=0\)。 |  |
| \(x=0\) | |
| 顶点是\((0,0)\)。 |
既然顶点是\((0,0)\),\(x\)-和\(y\)-截距都是点\((0,0)\)。 要绘制抛物线图,我们需要更多的点。 在这种情况下,最容易选择的值\(y\)。
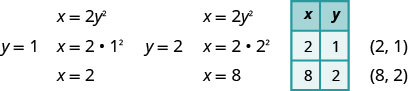
我们还绘制了\((2,1)\)与\((8,2)\)\(y\)-轴对称的点,即点\((2,−1),(8,−2)\)。
绘制抛物线图。
使用属性绘\(x=y^{2}\)制图表。
- 回答
-
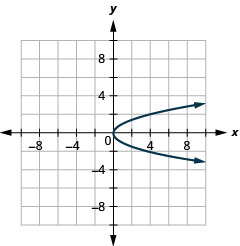
图 11.2.40
使用属性绘\(x=-y^{2}\)制图表。
- 回答
-
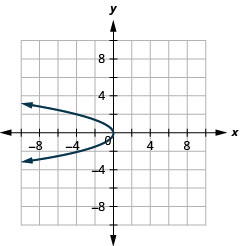
图 11.2.41
在下一个示例中,顶点不是原点。
使用属性绘\(x=-y^{2}+2 y+8\)制图表。
解决方案:
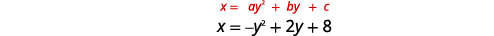 |
|
| 从那以后\(a=-1\),抛物线向左打开。 | |
 |
|
| 要找到对称轴,请 找到\(y=-\dfrac{b}{2 a}\) |
\(y=-\dfrac{b}{2 a}\) |
| \(y=-\dfrac{2}{2(-1)}\) | |
| \(y=1\) | |
| 对称轴是\(y=1\)。 | |
| 顶点在线上\(y=1\)。 | \(x=-y^{2}+2 y+8\) |
| 让\(y=1\)。 | 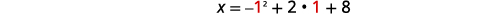 |
| \(x=9\) | |
| 顶点是\((9,1)\)。 | |
| \(x\)-截距发生在\(y=0\). | \(x=-y^{2}+2 y+8\) |
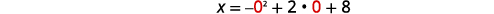 |
|
| \(x=8\) | |
| \(x\)-截距为\((8,0)\)。 | |
| 该点\((8,0)\)位于 对称线下方一个单位。 比对称线 上方一个单位的对称点是\((8,2)\) |
对称点是\((8,2)\)。 |
| \(y\)-截距发生在\(x=0\). | \(x=-y^{2}+2 y+8\) |
| 替代\(x=0\)。 | \(0=-y^{2}+2 y+8\) |
| 解决。 | \(y^{2}-2 y-8=0\) |
| \((y-4)(y+2)=0\) | |
| \(y=4, \quad y=-2\) | |
| \(y\)-intercepts 是\((0,4)\)和\((0,-2)\)。 | |
| 连接点以绘制抛物线。 | 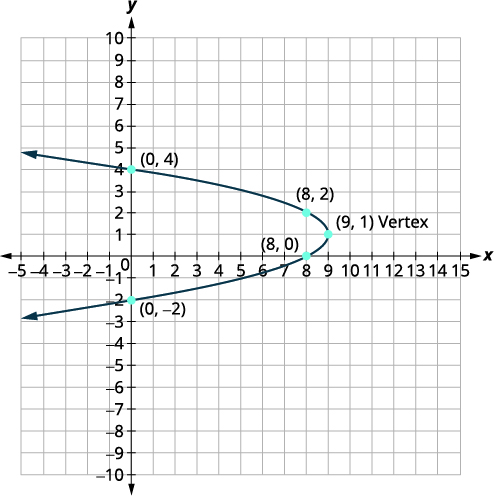 |
使用属性绘\(x=-y^{2}-4 y+12\)制图表。
- 回答
-
图 11.2.58
使用属性绘\(x=-y^{2}+2 y-3\)制图表。
- 回答
-
图 11.2.59
在表 11.2.4 中,我们看到了标准形式的方程与抛物线特性之间的关系。 操作方法框列出了以标准形式绘制抛物线的步骤\(x=a(y-k)^{2}+h\)。 我们将在下一个示例中使用此过程。
\(x=2(y-2)^{2}+1\)使用属性绘制图表。
解决方案:
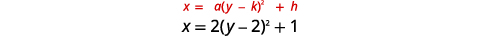 |
|
| 识别常量\(a, h, k\)。 | \(a=2, h=1, k=2\) |
| 因为\(a=2\),抛物线向右打开。 | |
 |
|
| 对称轴是\(y=k\)。 | 对称轴是\(y=2\)。 |
| 顶点是\((h,k)\)。 | 顶点是\((1,2)\)。 |
| 通过替换找到\(x\)-截距\(y=0\)。 | \(x=2(y-2)^{2}+1\) \(x=2(0-2)^{2}+1\) \(x=9\) |
| \(x\)-截距为\((9,0)\)。 | |
| 找到与对称轴\((9,0)\)对称的点。 | \((9,4)\) |
| 找到\(y\)-截图。 让\(x=0\)。 | \(\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}\) |
| 正方形不能为负,因此没有真正的解。 所以没有\(y\)-intercepts。 | |
| 绘制抛物线图。 | 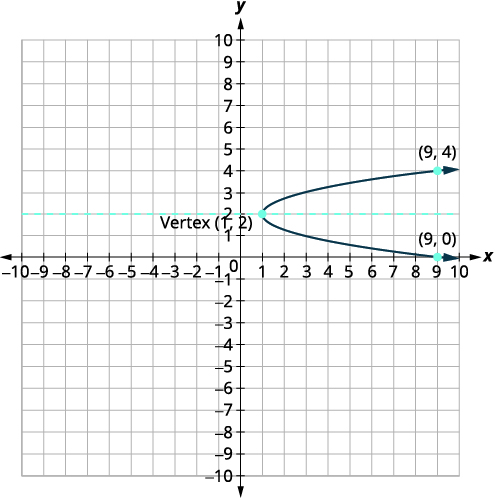 |
\(x=3(y-1)^{2}+2\)使用属性绘制图表。
- 回答
-
图 11.2.63
\(x=2(y-3)^{2}+2\)使用属性绘制图表。
- 回答
-
图 11.2.64
在下一个示例中,我们注意到 a 是负数,因此抛物线向左打开。
\(x=-4(y+1)^{2}+4\)使用属性绘制图表。
解决方案:
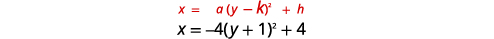 |
|
| 识别常量\(a, h, k\)。 | \(a=-4, h=4, k=-1\) |
| 从那以后\(a=-4\),抛物线向左打开。 | |
 |
|
| 对称轴是\(y=k\)。 | 对称轴是\(y=-1\)。 |
| 顶点是\((h,k)\)。 | 顶点是\((4,-1)\)。 |
| 通过替换找到\(x\)-截距\(y=0\)。 | \(x=-4(y+1)^{2}+4\) \(x=-4(0+1)^{2}+4\) \(x=0\) |
| \(x\)-截距为\((0,0)\)。 | |
| 找到与对称轴\((0,0)\)对称的点。 | \((0,-2)\) |
| 找到\(y\)-截图。 | \(x=-4(y+1)^{2}+4\) |
| 让\(x=0\)。 | \(\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}\) |
| \(y=-1+1 \quad y=-1-1\) | |
| \(y=0 \quad\quad y=-2\) | |
| \(y\)-intercepts 是\((0,0)\)和\((0,-2)\)。 | |
| 绘制抛物线图。 | 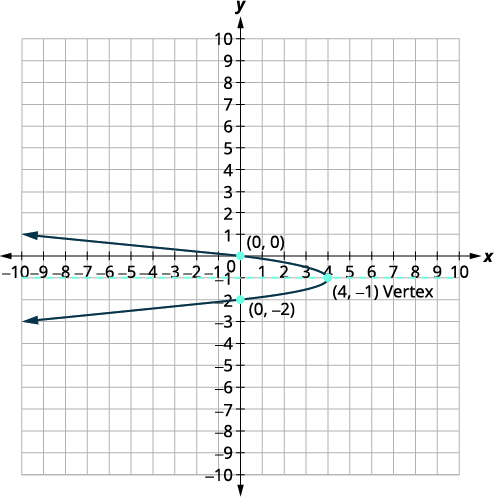 |
\(x=-4(y+2)^{2}+4\)使用属性绘制图表。
- 回答
-
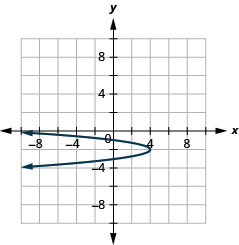
图 11.2.68
\(x=-2(y+3)^{2}+2\)使用属性绘制图表。
- 回答
-
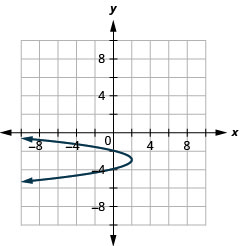
图 11.2.69
下一个示例要求我们首先将方程设置为标准形式,然后使用属性。
\(x=2 y^{2}+12 y+17\)以标准形式书写,然后使用标准形式的属性绘制方程图。
解决方案:
| \(x=2 y^{2}+12 y+17\) | |
| 通过填写正方\(x=a(y-k)^{2}+h\)形来重写表单中的函数。 | \(x=2\left(y^{2}+6 y\right)+17\) |
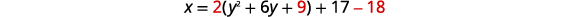 |
|
| \(x=2(y+3)^{2}-1\) | |
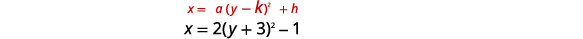 |
|
| 识别常量\(a, h, k\)。 | \(a=2, h=-1, k=-3\) |
| 因为\(a=2\),抛物线向右打开。 | |
 |
|
| 对称轴是\(y=k\)。 | 对称轴是\(y=-3\)。 |
| 顶点是\((h,k)\)。 | 顶点是\((-1,-3)\)。 |
| 通过替换找到\(x\)-截距\(y=0\)。 | \(x=2(y+3)^{2}-1\) \(x=2(0+3)^{2}-1\) \(x=17\) |
| \(x\)-截距为\((17,0)\)。 | |
| 找到与对称轴\((17,0)\)对称的点。 | \((17,-6)\) |
|
找到\(y\)-截图。 让\(x=0\)。 |
\(\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}\) |
| \(y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}\) | |
| \(y \approx-2.3 \quad y \approx-3.7\) | |
| \(y\)-intercepts 是\(\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)\)。 | |
| 绘制抛物线图。 | 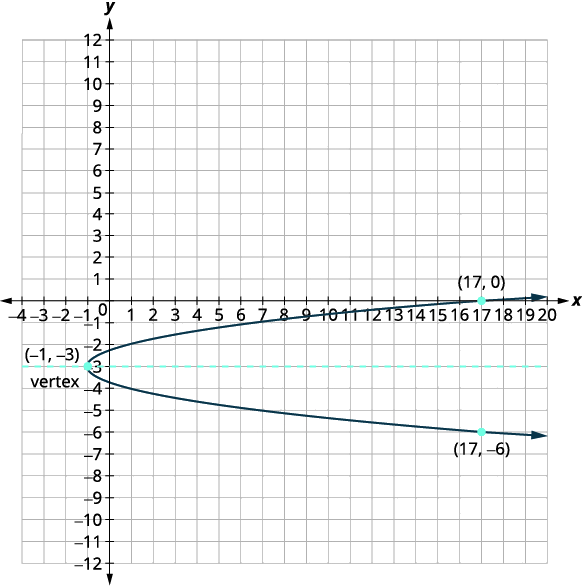 |
- \(x=3 y^{2}+6 y+7\)以标准形式书写然后
- 使用标准形式的属性绘制方程图。
- 回答
-
- \(x=3(y+1)^{2}+4\)
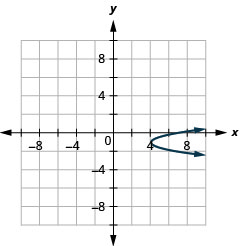
图 11.2.77
- \(x=-4 y^{2}-16 y-12\)以标准形式书写然后
- 使用标准形式的属性绘制方程图。
- 回答
-
- \(x=-4(y+2)^{2}+4\)
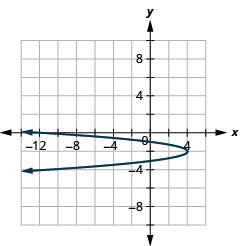
图 11.2.78
使用抛物线求解应用程序
许多建筑设计都包含抛物线。 正如我们将在下一个示例中看到的那样,使用抛物线建造桥梁的情况并不少见。
找出在所示桥梁基础上形成的抛物线拱的方程。 用标准形式写出方程式。
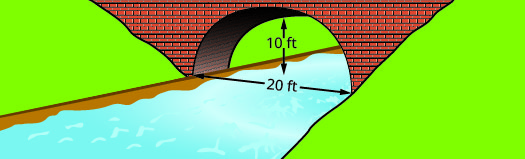
解决方案:
我们将首先设置一个坐标系并绘制抛物线。 该图将为我们提供以标准形式书写图表方程所需的信息\(y=a(x-h)^{2}+k\)。
|
让桥的左下角作为该点坐标网格的原点\((0,0)\)。 由于底部宽度为\(20\)英尺,因此该点\((20,0)\)代表右下角。 这座桥的最高点有 10 英尺高。 最高点是抛物线的顶点,因此 |
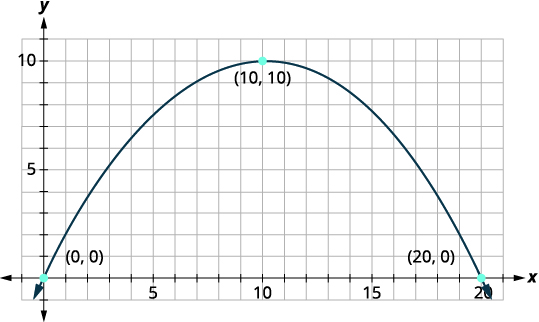 |
| 识别顶点,\((h,k)\)。 | \((h, k)=(10,10)\) |
| \(h=10, \quad k=10\) | |
|
将这些值替换为标准格式。 的值仍\(a\)未知。 要找到值,\(a\)请使用抛物线上的其他点之一。 |
\(\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}\) |
| 将另一个点的值代入方程中。 | \(y=a(x-10)^{2}+10\) \(0=a(0-10)^{2}+10\) |
| 求解\(a\)。 | \(\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}\) |
| \(y=a(x-10)^{2}+10\) | |
| 将的值替换\(a\)到方程中。 | \(y=-\dfrac{1}{10}(x-10)^{2}+10\) |
找出在所示桥梁基础上形成的抛物线拱的方程。 用标准形式写出方程式。
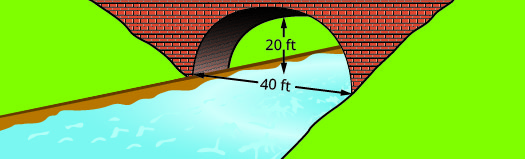
- 回答
-
\(y=-\dfrac{1}{20}(x-20)^{2}+20\)
找出在所示桥梁基础上形成的抛物线拱的方程。 用标准形式写出方程式。
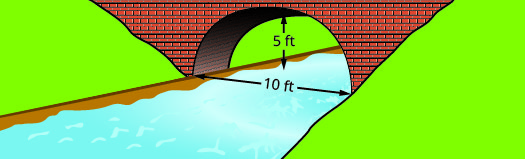
- 回答
-
\(y=-\dfrac{1}{5} x^{2}+2 x y=-\dfrac{1}{5}(x-5)^{2}+5\)
访问这些在线资源,获取有关二次函数和抛物线的更多说明和练习。
- 二次函数
- 圆锥和绘制水平抛物线简介
关键概念
- 抛物线:抛物线是平面中与定点和固定线距离相同的所有点。 定点称为焦点,固定线称为抛物线的直线。
垂直抛物线
|
通用表格 \(y=a x^{2}+b x+c\) |
标准表单 \(y=a(x-h)^{2}+k\) |
|
|---|---|---|
| 方向 | \ (y=a x^ {2} +b x+c\)” >\(a>0\) 向上;\(a<0\)向下 | \ (y=a (x-h) ^ {2} +k\)” >\(a>0\) 向上;\(a<0\)向下 |
| 对称轴 | \ (y=a x^ {2} +b x+c\)” >\(x=-\dfrac{b}{2 a}\) | \ (y=a (x-h) ^ {2} +k\)” >\(x=h\) |
| 顶点 | \ (y=a x^ {2} +b x+c\)” >替换\(x=-\dfrac{b}{2 a}\)并 求解\(y .\) |
\ (y=a (x-h) ^ {2} +k\)” >\((h, k)\) |
| \(y\)-截距 | \ (y=a x^ {2} +b x+c\)” >Let\(x=0\) | \ (y=a (x-h) ^ {2} +k\)” >Let\(x=0\) |
| \(x\)-拦截 | \ (y=a x^ {2} +b x+c\)” >Let\(y=0\) | \ (y=a (x-h) ^ {2} +k\)” >Let\(y=0\) |
- 如何绘制垂直抛物线图\(y=a x^{2}+b x+c\)或\(f(x)=a(x-h)^{2}+k)\)使用属性。
- 确定抛物线是向上还是向下打开。
- 找到对称轴。
- 找到顶点。
- 找到\(y\)截距。 在对称轴上找到\(y\)与-截距对称的点。
- 找到\(x\)-截图。
- 绘制抛物线图。
水平抛物线
|
通用表格 \(x=a y^{2}+b y+c\) |
标准表单 \(x=a(y-k)^{2}+h\) |
|
|---|---|---|
| 方向 | \ (x=a y^ {2} +b y+c\) “>\(a>0\) 右;\(a<0\)左 | \ (x=a (y-k) ^ {2} +h\) “>\(a>0\) 右;\(a<0\)左 |
| 对称轴 | \ (x=a y^ {2} +b y+c\)” >\(y=-\dfrac{b}{2 a}\) | \ (x=a (y-k) ^ {2} +h\)” >\(y=k\) |
| 顶点 | \ (x=a y^ {2} +b y+c\)” >替换\(y=-\dfrac{b}{2 a}\)并 求解\(x .\) |
\ (x=a (y-k) ^ {2} +h\)” >\((h, k)\) |
| \(x\)-拦截 | \ (x=a y^ {2} +b y+c\)” >Let\(x=0\) | \ (x=a (y-k) ^ {2} +h\)” >Let\(x=0\) |
| \(y\)-截距 | \ (x=a y^ {2} +b y+c\)” >Let\(y=0\) | \ (x=a (y-k) ^ {2} +h\)” >Let\(y=0\) |

如何绘制水平抛物线图\(x=a y^{2}+b y+c\)或\(x=a(y-k)^{2}+h\)使用属性。
- 确定抛物线是向左还是向右打开。
- 找到对称轴。
- 找到顶点。
- 找到\(x\)截距。 在对称轴上找到\(x\)与-截距对称的点。
- 找到\(y\)-截图。
- 绘制抛物线图。
词汇表
- 抛物线
- 抛物线是平面中与定点和固定线距离相同的所有点。


