Skip to main content
Global

11.2E：练习

  1. Last updated
  2. Save as PDF
  • Page ID
    204416

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    练习成就完美

    练习\(\PageIndex{23}\) Use the Distance Formula

    在以下练习中，找出两点之间的距离。 以精确的形式写出答案，然后找到十进制近似值，必要时四舍五入到最接近的十分之一。

    1. \((2,0)\)和\((5,4)\)
    2. \((-4,-3)\)和\((2,5)\)
    3. \((-4,-3)\)和\((8,2)\)
    4. \((-7,-3)\)和\((8,5)\)
    5. \((-1,4)\)和\((2,0)\)
    6. \((-1,3)\)和\((5,-5)\)
    7. \((1,-4)\)和\((6,8)\)
    8. \((-8,-2)\)和\((7,6)\)
    9. \((-3,-5)\)和\((0,1)\)
    10. \((-1,-2)\)和\((-3,4)\)
    11. \((3,-1)\)和\((1,7)\)
    12. \((-4,-5)\)和\((7,4)\)
    回答

    1。 \(d=5\)

    3。 \(13\)

    5。 \(5\)

    7。 \(13\)

    9。 \(d=3 \sqrt{5}, d \approx 6.7\)

    11。 \(d=\sqrt{68}, d \approx 8.2\)

    练习\(\PageIndex{24}\) Use the Midpoint Formula

    在以下练习中，

    1. 找到给定端点的线段的中点，然后
    2. 在矩形坐标系上绘制端点和中点。
    1. \((0,-5)\)和\((4,-3)\)
    2. \((-2,-6)\)和\((6,-2)\)
    3. \((3,-1)\)和\((4,-2)\)
    4. \((-3,-3)\)和\((6,-1)\)
    回答

    1。

    1. 中点：\((2,-4)\)
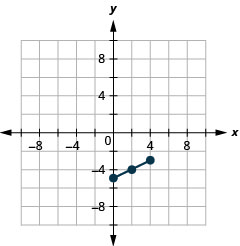
    此图显示了具有端点（0，负 5）和（4，负 3）和中点（2，负 4）的线段。
    图 11.1.42

    3。

    1. 中点：\(\left(3 \frac{1}{2},-1 \frac{1}{2}\right)\)
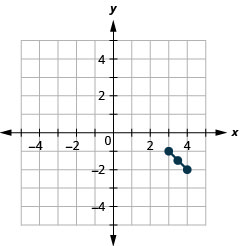
    此图显示了具有端点（3，负 1）和（4，负 2）和中点（3 半，负 1 半）的线段。
    图 11.1.43
    练习\(\PageIndex{25}\) Write the Equation of a Circle in Standard Form

    在以下练习中，写出具有给定半径和中心的圆方程的标准形式\((0,0)\)。

    1. 半径：\(7\)
    2. 半径：\(9\)
    3. 半径：\(\sqrt{2}\)
    4. 半径：\(\sqrt{5}\)
    回答

    1。 \(x^{2}+y^{2}=49\)

    3。 \(x^{2}+y^{2}=2\)

    练习\(\PageIndex{26}\) Write the Equation of a Circle in Standard Form

    在以下练习中，写出具有给定半径和中心的圆方程的标准形式

    1. 半径：\(1\)，中心：\((3,5)\)
    2. 半径：\(10\)，中心：\((-2,6)\)
    3. 半径：\(2.5\)，中心：\((1.5, -3.5)\)
    4. 半径：\(1.5\)，中心：\((-5.5, -6.5)\)
    回答

    1。 \((x-3)^{2}+(y-5)^{2}=1\)

    3。 \((x-1.5)^{2}+(y+3.5)^{2}=6.25\)

    练习\(\PageIndex{27}\) Write the Equation of a Circle in Standard Form

    在以下练习中，写出圆方程的标准形式，给定中心在圆上加点。

    1. \((3,−2)\)以点为中心\((3,6)\)
    2. \((6,−6)\)以点为中心\((2,−3)\)
    3. \((4,4)\)以点为中心\((2,2)\)
    4. \((−5,6)\)以点为中心\((−2,3)\)
    回答

    1。 \((x-3)^{2}+(y+2)^{2}=64\)

    3。 \((x-4)^{2}+(y-4)^{2}=8\)

    练习\(\PageIndex{28}\) Graph a Circle

    在以下练习中，

    1. 找到中心和半径，然后
    2. 绘制每个圆圈的图形。
    1. \((x+5)^{2}+(y+3)^{2}=1\)
    2. \((x-2)^{2}+(y-3)^{2}=9\)
    3. \((x-4)^{2}+(y+2)^{2}=16\)
    4. \((x+2)^{2}+(y-5)^{2}=4\)
    5. \(x^{2}+(y+2)^{2}=25\)
    6. \((x-1)^{2}+y^{2}=36\)
    7. \((x-1.5)^{2}+(y+2.5)^{2}=0.25\)
    8. \((x-1)^{2}+(y-3)^{2}=\frac{9}{4}\)
    9. \(x^{2}+y^{2}=64\)
    10. \(x^{2}+y^{2}=49\)
    11. \(2 x^{2}+2 y^{2}=8\)
    12. \(6 x^{2}+6 y^{2}=216\)
    回答

    1。

    1. 圆的中心位置为\((−5,−3)\)，半径为\(1\)。
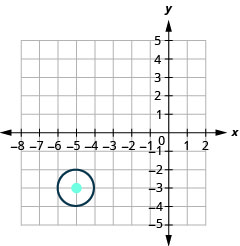
    此图显示了一个圆心（负 5，负 3），半径为 1。
    图 11.1.44

    3。

    1. 圆的中心位置为\((4,−2)\)，半径为\(4\)。
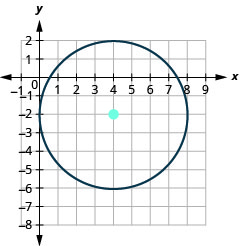
    此图显示了中心为 (4，负 2)、半径为 4 的圆。
    图 11.1.45

    5。

    1. 圆的中心位置为\((0,−2)\)，半径为\(5\)。
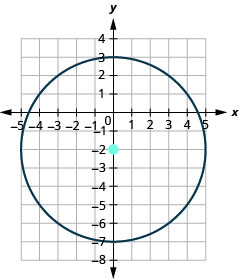
    此图显示了中心为（负 2, 5）且半径为 5 的圆。
    图 11.1.46

    7。

    1. 圆的中心位置为\((1.5,2.5)\)，半径为\(0.5\)。
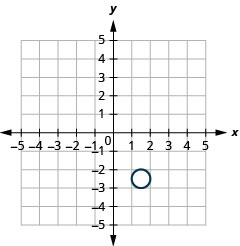
    此图显示了中心为 (1.5, 2.5) 且半径为 0.5 的圆
    图 11.1.47

    9。

    1. 圆的中心位置为\((0,0)\)，半径为\(8\)。
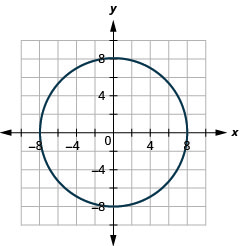
    此图显示了中心为 (0, 0) 且半径为 8 的圆。
    图 11.1.48

    11。

    1. 圆的中心位置为\((0,0)\)，半径为\(2\)。
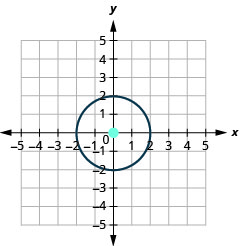
    此图显示了中心为 (0, 0) 且半径为 2 的圆。
    图 11.1.49
    练习\(\PageIndex{29}\) Graph a Circle

    在以下练习中，

    1. 确定中心和半径以及
    2. 图形。
    1. \(x^{2}+y^{2}+2 x+6 y+9=0\)
    2. \(x^{2}+y^{2}-6 x-8 y=0\)
    3. \(x^{2}+y^{2}-4 x+10 y-7=0\)
    4. \(x^{2}+y^{2}+12 x-14 y+21=0\)
    5. \(x^{2}+y^{2}+6 y+5=0\)
    6. \(x^{2}+y^{2}-10 y=0\)
    7. \(x^{2}+y^{2}+4 x=0\)
    8. \(x^{2}+y^{2}-14 x+13=0\)
    回答

    1。

    1. 中心:\((−1,−3)\)，半径：\(1\)
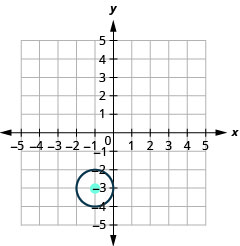
    此图显示了中心为（负 1，负 3）且半径为 1 的圆。
    图 11.1.49

    3。

    1. 中心:\((2,−5)\)，半径：\(6\)
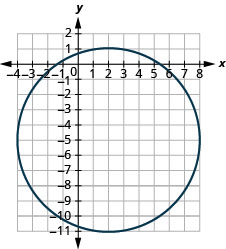
    此图显示了中心为 (2，负 5)、半径为 6 的圆。
    图 11.1.50

    5。

    1. 中心:\((0,−3)\)，半径：\(2\)
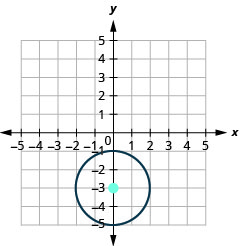
    此图显示了中心为 (0，负 3)、半径为 2 的圆。
    图 11.1.51

    7。

    1. 中心:\((−2,0)\)，半径：\(-2\)
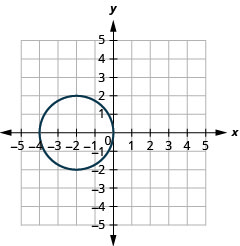
    此图显示了中心为（负 2, 0）且半径为 2 的圆。
    图 11.1.52
    练习\(\PageIndex{30}\) Writing Exercises
    1. 解释距离公式和圆方程之间的关系。
    2. 圆圈是函数吗？ 解释原因或原因。
    3. 用你自己的话说，说明圆的定义。
    4. 用你自己的话说，解释一下你将圆方程的一般形式更改为标准形式所要采取的步骤。
    回答

    1。 答案会有所不同。

    3。 答案会有所不同。

    自检

    a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

    。
    图 11.1.53

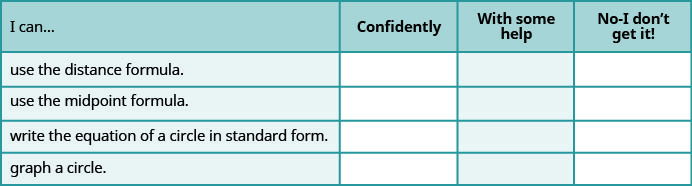
    b. 如果您的大部分支票是：

    ... 自信地。 恭喜！ 您已经实现了本节中的目标。 反思一下你使用的学习技能，这样你就可以继续使用它们。 为了确信自己有能力做这些事情，你做了什么？ 具体一点。

    ... 在一些帮助下。 必须迅速解决这个问题，因为你不掌握的话题会成为你通往成功之路的坑洼。 在数学中，每个主题都建立在以前的工作基础上。 在继续前进之前，请务必确保自己有坚实的基础。 你能向谁寻求帮助？ 你的同学和老师都是很好的资源。 校园里有没有可以提供数学导师的地方？ 你的学习技能可以提高吗？

    ... 不-我不明白！ 这是一个警告信号，你一定不能忽视它。 你应该立即得到帮助，否则你很快就会不知所措。 尽快与您的教师见面，讨论您的情况。 你可以一起制定一个计划，为你提供所需的帮助。