11.2:距离和中点公式和圆形
- Page ID
- 204397
在本节结束时,您将能够:
- 使用距离公式
- 使用中点公式
- 用标准形式写出圆的方程
- 画一个圆圈
在开始之前,请参加这个准备测验。
- 找出腿为\(12\)和\(16\)英寸的直角三角形的斜边长度。
如果你错过了这个问题,请查看示例 2.34。 - 因子:\(x^{2}-18 x+81\)。
如果您错过了此问题,请查看示例 6.24。 - 通过完成方块求解:\(x^{2}-12 x-12=0\).
如果您错过了此问题,请查看示例 9.22。
在本章中,我们将研究圆锥截面(通常称为圆锥)及其属性。 圆锥是由平面与双锥相交而形成的曲线,两个圆锥点对点放置。 双锥的每一半都称为午睡。
有四个圆锥—— 圆形、抛物线、椭圆和双曲线。 下图显示了与双锥相交的平面是如何形成每条曲线的。
每条曲线都有许多影响您日常生活的应用,从手机到声学和导航系统。 在本节中,我们将研究圆的属性。
使用距离公式
我们使用毕达哥拉斯定理来计算直角三角形边的长度。 在这里,我们将再次使用这个定理来查找矩形坐标系上的距离。 通过在矩形坐标系上寻找距离,我们可以在圆锥和代数的几何之间建立联系,这为应用开辟了一个充满机会的世界。
我们的第一步是开发一个公式来计算矩形坐标系上各点之间的距离。 我们将绘制点并创建一个直角三角形,就像我们在图表和函数中找到斜率时所做的那样。 然后我们更进一步,使用毕达哥拉斯定理来找出三角形斜边的长度,即两点之间的距离。
使用直角坐标系查找点\((6,4)\)和之间的距离\((2,1)\)。
解决方案
| 绘制这两个点。 用一条线将两 点连接起来。 画一个直角三角形,就好像你要 找到斜率一样。 |
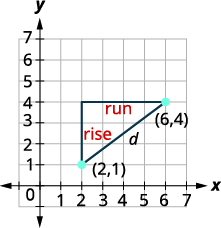
|
| 找出每条腿的长度。 |
|
| 使用毕达哥拉斯定理找出\(d\)两点之间的距离。 | \(a^{2}+b^{2}=c^{2}\) |
| 在值中替换。 | \(3^{2}+4^{2}=d^{2}\) |
| 简化。 | \(9+16=d^{2}\) |
| \(25=d^{2}\) | |
| 使用平方根属性。 | \(d=5\quad\cancel{d=-5}\) |
| 既然距离\(d\)是正数,我们可以消除\(d=-5\)。 | 点\((6,4)\)与之间的距离\((2,1)\)为\(5\)。 |
使用直角坐标系查找点\((6,1)\)和之间的距离\((2,-2)\)。
- 回答
-
\(d=5\)
使用直角坐标系查找点\((5,3)\)和之间的距离\((-3,-3)\)。
- 回答
-
\(d=10\)
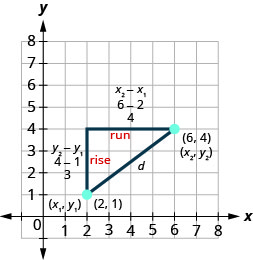
我们在上一个示例中使用的方法引导我们得出计算两点\(\left(x_{1}, y_{1}\right)\)和之间距离的公式\(\left(x_{2}, y_{2}\right)\)。
当我们找到水平腿的长度时\(6−2\),我们减去了\(x_{2}-x_{1}\)。
当我们找到垂直腿的长度时\(4−1\),我们减去了\(y_{2}-y_{1}\)。
如果三角形处于不同的位置,则我们可能减去了\(x_{1}-x_{2}\)或\(y_{1}-y_{2}\)。 表达式\(x_{2}-x_{1}\)和仅在结果数字的符号上\(x_{1}-x_{2}\)变化。 要获得正值,因为距离是正值,我们可以使用绝对值。 因此,总而言之,我们会说\(\left|x_{2}-x_{1}\right|\)和\(\left|y_{2}-y_{1}\right|\)。
在毕达哥拉斯定理中,我们用一般表达式\(\left|x_{2}-x_{1}\right|\)\(\left|y_{2}-y_{1}\right|\)而不是数字代替。
\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)
这是我们用来计算两点\(d\)\((x_{1},y_{1})\)之间距离的距离公式\((x_{2}, y_{2})\)。
距离公式
两点\((x_{1},y_{1})\)和\(d\)之间的距离\((x_{2}, y_{2})\)为
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
使用距离公式计算点\((-5,-3)\)和之间的距离\((7,2)\)。
解决方案:
写出距离公式。
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
标记积分\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\),\(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\)然后替换。
\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)
简化。
\(d=\sqrt{12^{2}+5^{2}}\)
\(d=\sqrt{144+25}\)
\(d=\sqrt{169}\)
\(d=13\)
答案:
\(d=13\)
使用距离公式计算点\((-4,-5)\)和之间的距离\((5,7)\)。
- 回答
-
\(d=15\)
使用距离公式计算点\((-2,-5)\)和之间的距离\((-14,-10)\)。
- 回答
-
\(d=13\)
使用距离公式计算点\((10,−4)\)和之间的距离\((−1,5)\)。 以精确的形式写出答案,然后找到十进制近似值,必要时四舍五入到最接近的十分之一。
解决方案:
写出距离公式。
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
标记积分\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\),\(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\)然后替换。
\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)
简化。
\(d=\sqrt{(-11)^{2}+9^{2}}\)
\(d=\sqrt{121+81}\)
\(d=\sqrt{202}\)
由于\(202\)不是完美的正方形,我们可以将答案保留为精确的形式或找到十进制近似值。
\(d=\sqrt{202}\)
或者
\(d \approx 14.2\)
使用距离公式计算点\((−4,−5)\)和之间的距离\((3,4)\)。 以精确的形式写出答案,然后找到十进制近似值,必要时四舍五入到最接近的十分之一。
- 回答
-
\(d=\sqrt{130}, d \approx 11.4\)
使用距离公式计算点\((−2,−5)\)和之间的距离\((−3,−4)\)。 以精确的形式写出答案,然后找到十进制近似值,必要时四舍五入到最接近的十分之一。
- 回答
-
\(d=\sqrt{2}, d \approx 1.4\)
使用中点公式
能够找到线段的中点通常很有用。 例如,如果您有圆直径的端点,则可能需要找到圆的中心,即直径的中点。 为了找到线段的中点,我们求出端点\(x\)-坐标的平均值和\(y\)-坐标的平均值。
中点公式
线段的中点,其端点是两点\(\left(x_{1}, y_{1}\right)\)并且\(\left(x_{2}, y_{2}\right)\)是
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
为了找到线段的中点,我们求出端点\(x\)-坐标的平均值和\(y\)-坐标的平均值。
使用中点公式求出端点为\((−5,−4)\)和的线段的中点\((7,2)\)。 在矩形坐标系上绘制端点和中点。
解决方案:
| 写出中点公式。 | \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\) |
| 标记积分,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-4}\end{array}\right), \left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\)然后替换。 | \(\left(\frac{-5+7}{2}, \frac{-4+2}{2}\right)\) |
| 简化。 | \(\left(\frac{2}{2}, \frac{-2}{2}\right)\) |
|
\((1,-1)\) 线段的中点就是点 \((1,-1)\)。 |
|
| 绘制端点和中点。 |
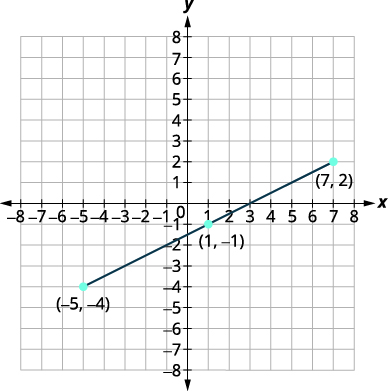
|
使用中点公式求出端点为\((−3,−5)\)和的线段的中点\((5,7)\)。 在矩形坐标系上绘制端点和中点。
- 回答
-
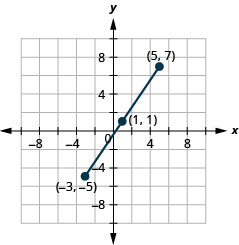
图 11.1.7
使用中点公式求出端点为\((−2,−5)\)和的线段的中点\((6,−1)\)。 在矩形坐标系上绘制端点和中点。
- 回答
-
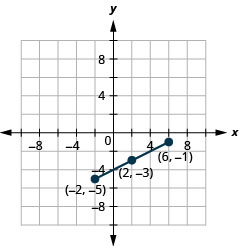
图 11.1.8
距离公式和中点公式都取决于两个点,\(\left(x_{1}, y_{1}\right)\)和\(\left(x_{2}, y_{2}\right)\)。 很容易混淆哪个公式需要加法和哪个减法坐标。 如果我们记住公式来自哪里,可能更容易记住公式。
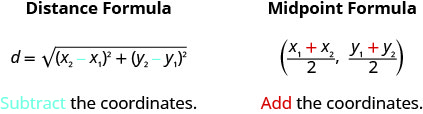
用标准形式写出圆的方程
正如我们提到的,我们的目标是将圆锥的几何与代数连接起来。 通过使用坐标平面,我们可以轻松做到这一点。
我们将圆定义为平面中与平面中给定点保持固定距离的所有点。 给定点称为圆的中心\((h,k)\),固定距离称为圆的半径。\(r\)
圆是平面中与平面中给定点保持固定距离的所有点。 给定点称为圆的中心\((h,k)\),固定距离称为圆的半径。\(r\)
我们看矩形坐标系中的一个圆。 半径是从中心到圆上某一 点的距离\((x,y)\)。\((h,k)\) |
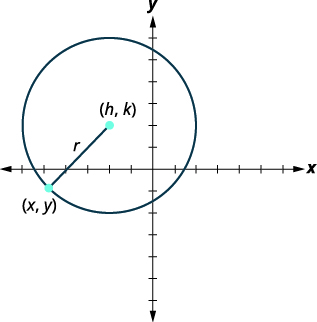
|
| 要得出圆的方程,我们可以使用带点\((h,k)\)\((x,y)\)和 距离的 距离公式\(r\)。 |
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| 替换这些值。 | \(r=\sqrt{(x-h)^{2}+(y-k)^{2}}\) |
| 两边都是正方形。 | \(r^{2}=(x-h)^{2}+(y-k)^{2}\) |
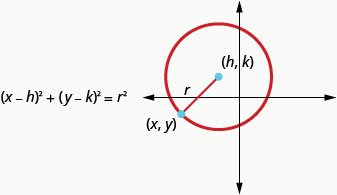
这是中心和半径为的圆方程\((h,k)\)的标准形式\(r\)。
中心、\((h,k)\)和半径为的圆方程的标准形式是\(r\)
用半径\(3\)和中心写出圆方程的标准形式\((0,0)\)。
解决方案:
| 使用圆方程的标准形式 | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| 在值中替换\(r=3, h=0\),和\(k=0\)。 | \((x-0)^{2}+(y-0)^{2}=3^{2}\) |
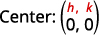 |
|
| 简化。 | \(x^{2}+y^{2}=9\) |
写出半径为\(6\)和中心的圆方程的标准形式\((0,0)\)。
- 回答
-
\(x^{2}+y^{2}=36\)
写出半径为\(8\)和中心的圆方程的标准形式\((0,0)\)。
- 回答
-
\(x^{2}+y^{2}=64\)
在最后一个例子中,中心是\((0,0)\)。 注意方程发生了什么。 无论中心在哪里\((0,0)\),标准形式就会变成\(x^{2}+y^{2}=r^{2}\)。
用半径\(2\)和中心写出圆方程的标准形式\((−1,3)\)。
解决方案:
| 使用圆方程的标准形式。 | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| 在值中替换。 | \((x-(-1))^{2}+(y-3)^{2}=2^{2}\) |
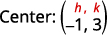 |
|
| 简化。 | \((x+1)^{2}+(y-3)^{2}=4\) |
写出半径为\(7\)和中心的圆方程的标准形式\((2,−4)\)。
- 回答
-
\((x-2)^{2}+(y+4)^{2}=49\)
写出半径为\(9\)和中心的圆方程的标准形式\((−3,−5)\)。
- 回答
-
\((x+3)^{2}+(y+5)^{2}=81\)
在下一个示例中,没有给出半径。 为了计算半径,我们使用两个给定点的距离公式。
写出圆方程的标准形式\((2,4)\),中心也包含点\((−2,1)\)。
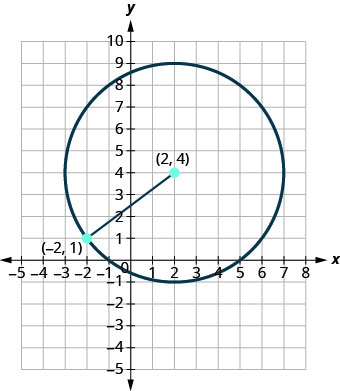
解决方案:
半径是从圆心到圆上任何点的距离,因此我们可以使用距离公式来计算。 我们将使用中心\((2,4)\)和点\((−2,1)\)
使用距离公式求出半径。
\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
替换这些值。 \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)
\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)
简化。
\(r=\sqrt{(-4)^{2}+(-3)^{2}}\)
\(r=\sqrt{16+9}\)
\(r=\sqrt{25}\)
\(r=5\)
现在我们知道了半径和中心\((2,4)\),我们可以使用圆方程的标准形式来找到方程。\(r=5\)
使用圆方程的标准形式。
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
在值中替换。
\((x-2)^{2}+(y-4)^{2}=5^{2}\)
简化。
\((x-2)^{2}+(y-4)^{2}=25\)
写出圆方程的标准形式\((2,1)\),中心也包含点\((−2,−2)\)。
- 回答
-
\((x-2)^{2}+(y-1)^{2}=25\)
写出圆方程的标准形式\((7,1)\),中心也包含点\((−1,−5)\)。
- 回答
-
\((x-7)^{2}+(y-1)^{2}=100\)
画一个圆圈
任何形式的方程\((x-h)^{2}+(y-k)^{2}=r^{2}\)都是圆方程的标准形式\((h,k)\),其中心和半径为\(r\)。 然后,我们可以在矩形坐标系上绘制圆的图形。
请注意,标准格式要求从\(x\)和中减去\(y\)。 在下一个例子中,方程有\(x+2\),所以我们需要将加法重写为负数的减法。
找到中心和半径,然后绘制圆的图形:\((x+2)^{2}+(y-1)^{2}=9\)。
解决方案:
 |
|
|
使用圆方程的标准形式。 确定中心\((h,k)\)和半径\(r\)。 |
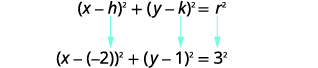 |
| 中心:\((-2,1)\)半径:\(3\) | |
| 绘制圆圈图。 | 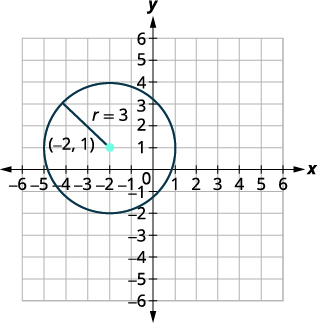 |
- 找到中心和半径,然后
- 绘制圆圈图:\((x-3)^{2}+(y+4)^{2}=4\).
- 回答
-
- 圆的中心位置为\((3,-4)\),半径为\(2\)。
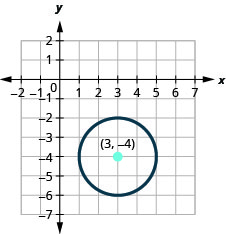
图 11.1.19
- 找到中心和半径,然后
- 绘制圆圈图:\((x-3)^{2}+(y-1)^{2}=16\).
- 回答
-
- 圆的中心位置为\((3,1)\),半径为\(4\)。
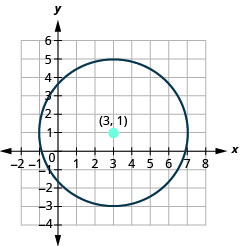
图 11.1.20
要找到中心和半径,我们必须用标准形式写出方程。 在下一个示例中,我们必须首先将的系数\(x^{2}, y^{2}\)设为一。
找到中心和半径,然后绘制圆的图形\(4 x^{2}+4 y^{2}=64\)。
解决方案:
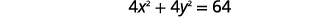 |
|
| 将两边除以\(4\)。 | 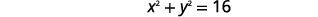 |
| 使用圆方程的标准形式。 确定中心\((h,k)\)和半径\(r\)。 |
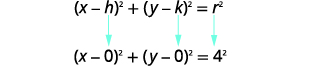 |
| 中心:\((0,0)\)半径:\(4\) | |
| 绘制圆圈图。 | 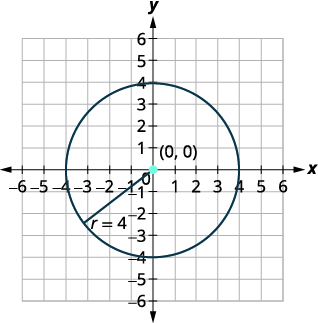 |
- 找到中心和半径,然后
- 绘制圆圈图:\(3 x^{2}+3 y^{2}=27\)
- 回答
-
- 圆的中心位置为\((0,0)\),半径为\(3\)。
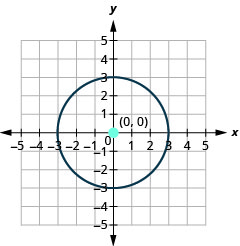
图 11.1.25
- 找到中心和半径,然后
- 绘制圆圈图:\(5 x^{2}+5 y^{2}=125\)
- 回答
-
- 圆的中心位置为\((0,0)\),半径为\(5\)。
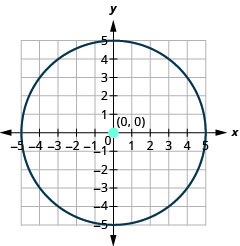
图 11.1.26
如果我们扩展示例 11.1.8 中的方程\((x+2)^{2}+(y-1)^{2}=9\),则圆的方程看起来会大不相同。
\((x+2)^{2}+(y-1)^{2}=9\)
对二项式进行平方。
\(x^{2}+4 x+4+y^{2}-2 y+1=9\)
按降序排列术语,然后在右边取零
\(x^{2}+y^{2}+4 x-2 y-4=0\)
这种形式的方程被称为圆方程的一般形式。
圆方程的一般形式是
\(x^{2}+y^{2}+a x+b y+c=0\)
如果给我们一个通用形式的方程,我们可以通过填写\(x\)和中的正方形将其更改为标准形式\(y\)。 然后我们可以使用圆的中心和半径绘制圆的图形。
- 找到中心和半径,然后
- 绘制圆圈图:\(x^{2}+y^{2}-4 x-6 y+4=0\)
解决方案:
我们需要将这个通用形式重写成标准形式才能找到中心和半径。
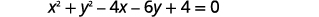
|
|
| 将\(x\)-terms\(y\) 和-terms 分组。 收集右侧的常量。 |
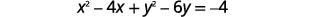
|
| 完成方格。 |
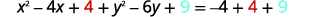
|
| 重写为二项式方块。 |
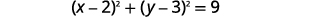
|
| 确定中心和半径。 | 中心:\((2,3)\)半径:\(3\) |
| 绘制圆圈图。 |
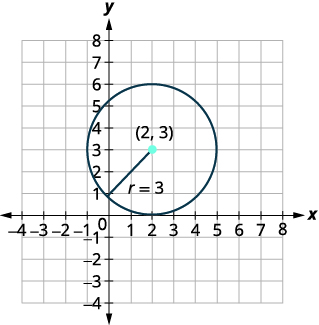
|
- 找到中心和半径,然后
- 绘制圆圈图:\(x^{2}+y^{2}-6 x-8 y+9=0\).
- 回答
-
- 圆的中心位置为\((3,4)\),半径为\(4\)。
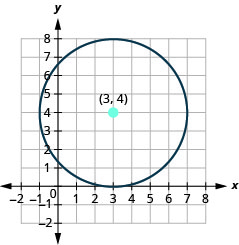
图 11.1.32
- 找到中心和半径,然后
- 绘制圆圈图:\(x^{2}+y^{2}+6 x-2 y+1=0\)
- 回答
-
- 圆的中心位置为\((-3,1)\),半径为\(3\)。
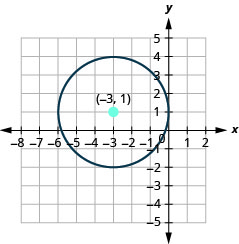
图 11.1.33
在下一个示例中,有一个\(y\)-term和一个\(y^{2}\)-term。 但是请注意,没有\(x\)-term,只有一个\(x^{2}\)-term。 我们以前见过这个,知道这意味着\(h\)是\(0\)。 我们需要完成项的平方,但不需要完成\(x\)项的平方。\(y\)
- 找到中心和半径,然后
- 绘制圆圈图:\(x^{2}+y^{2}+8 y=0\)
解决方案:
我们需要将这个通用形式重写成标准形式才能找到中心和半径。
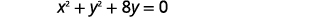 |
|
| 将\(x\)-terms\(y\) 和-terms 分组。 | 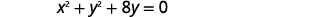 |
| 右侧没有要收集的常量。 | |
| 完成方块\(y^{2}+8y\)。 | 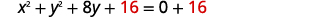 |
| 重写为二项式方块。 | 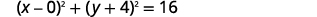 |
| 确定中心和半径。 | 中心:\((0,-4)\)半径:\(4\) |
| 绘制圆圈图。 | 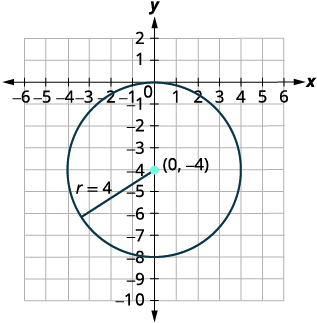 |
- 找到中心和半径,然后
- 绘制圆圈图:\(x^{2}+y^{2}-2 x-3=0\).
- 回答
-
- 圆的中心位置为\((-1,0)\),半径为\(2\)。
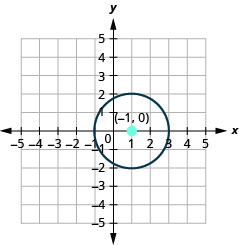
图 11.1.39
- 找到中心和半径,然后
- 绘制圆圈图:\(x^{2}+y^{2}-12 y+11=0\).
- 回答
-
- 圆的中心位置为\((0,6)\),半径为\(5\)。
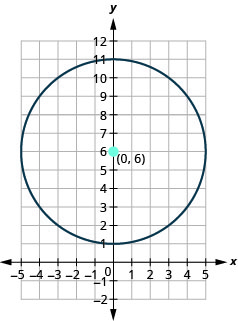
图 11.1.40
访问这些在线资源以获取更多说明和练习,使用距离和中点公式以及绘制圆圈。
- 距离中点公式和圆圈
- 找出两点之间的距离和中点
- 完成正方形以标准圆形写出方程
关键概念
- 距离公式:两点\(d\)\(\left(x_{1}, y_{1}\right)\)之间的距离\(\left(x_{2}, y_{2}\right)\)为
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
- 中点公式:线段的中点,其端点是两点\(\left(x_{1}, y_{1}\right)\)并且\(\left(x_{2}, y_{2}\right)\)是
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
为了找到线段的中点,我们求出端点\(x\)-坐标的平均值和\(y\)-坐标的平均值。 - 圆圈:圆是平面中与平面中固定点保持固定距离的所有点。 给定点称为圆的中心\((h,k)\),固定距离称为圆的半径。\(r\)
- 方程的标准形式 a Circle:具有中心\((h,k)\)、和半径的圆方程的标准形式是\(r\)
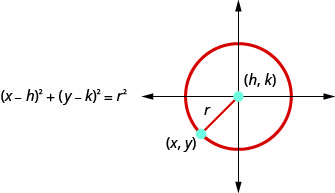
- 圆@@ 方程的一般形式:圆方程的一般形式是
\(x^{2}+y^{2}+a x+b y+c=0\)
词汇表
- 圈
- 圆是平面中与平面中固定点保持固定距离的所有点。


