11.4: 省略号
- Page ID
- 204433
在本节结束时,您将能够:
- 绘制一个以原点为中心的椭圆
- 找出以原点为中心的椭圆的方程
- 绘制中心不在原点的椭圆
- 用省略号求解应用程序
在开始之前,请参加这个准备测验。
- \(y=(x-1)^{2}-2\)使用转换绘制图表。
如果您错过了此问题,请查看示例 9.57。 - 完成正方形:\(x^{2}-8 x=8\).
如果您错过了此问题,请查看示例 9.12。 - 以标准形式书写。 \(y=2 x^{2}-12 x+14\)
如果您错过了此问题,请查看示例 9.59。
绘制以原点为中心的椭圆
我们要看的下一个圆锥截面是一个椭圆。 我们将椭圆定义为平面中的所有点,其中两个固定点的距离之和是恒定的。 每个给定点都称为椭圆的焦点。
椭圆是平面中的所有点,其中两个定点的距离之和是恒定的。 每个定点都称为椭圆的焦点。
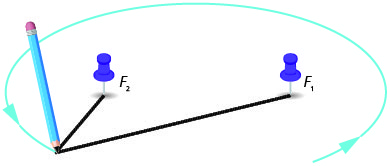
我们可以画一个椭圆,方法是拿一些固定长度的柔性绳子,然后将两端连接到两个图钉上。 我们用一支钢笔拉紧绳子,然后围绕两个图钉旋转。 生成的数字是一个椭圆。
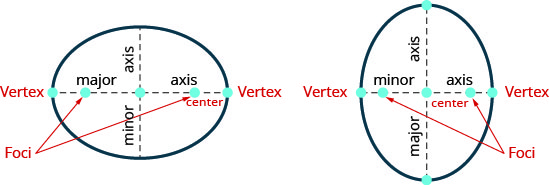
通过焦点绘制的直线在两点上与椭圆相交。 每个点都被称为椭圆的顶点。 连接顶点的线段称为长轴。 线段的中点称为椭圆的中心。 垂直于长轴、穿过中心并在两点上与椭圆相交的线段称为短轴。
我们前面提到过,我们的目标是将圆锥的几何与代数连接起来。 将椭圆放置在矩形坐标系上为我们提供了这样的机会。 在图中,我们放置了椭圆,使焦点\(((−c,0),(c,0))\)位于\(x\)-轴上,中心是原点。
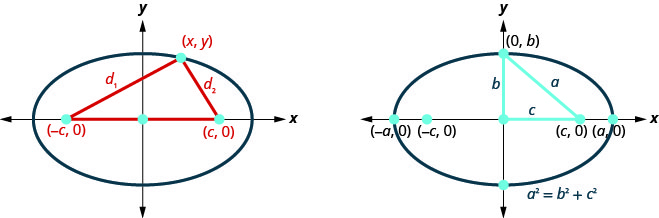
该定义指出,从焦点到点的距离之和\((x,y)\)是恒定的。 \(d_{1}+d_{2}\)所以,我们称之\(2a\)为常数\(d_{1}+d_{2}=2 a\)。 我们将使用距离公式来引导我们得出椭圆的代数公式。
\(d_{1} \quad+\quad \quad d_{2} \quad=\quad 2 a\)
使用距离公式查找\(d_{1},d_{2}\)。
\(\sqrt{(x-(-c))^{2}+(y-0)^{2}}+\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a\)
消除激进分子并简化后,我们得到:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1\)
为了简化椭圆的方程,我们假定\(a^{2}−c^{2}=b^{2}\)。所以,标准形式中以原点为中心的椭圆的方程为:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
要绘制椭圆图,了解截面会很有帮助。 我们将使用公式找到\(x\)-intercepts和\(y\)-intercepts。
\(y\)-拦截
让\(x=0\)。
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}+\frac{y^{2}}{a^{2}} &=1 \\ \frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=b^{2} \\ y &=\pm b \end{aligned}\)
\(y\)-intercepts 是\((0,b)\)和\((0, -b)\)。
\(x\)-拦截
让\(y=0\)。
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)
\(x\)-intercepts 是\((a,0)\)和\((-a,0)\)。
方程的标准形式是中心椭圆\((0,0)\)
中心\((0,0)\)椭圆方程的标准形式是
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
\(x\)-intercepts 是\((a,0)\)和\((−a,0)\)。
\(y\)-intercepts 是\((0,b)\)和\((0,−b)\)。
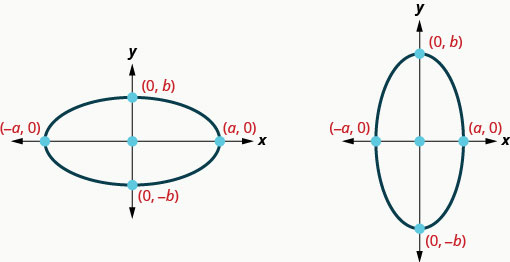
请注意,当长轴为水平轴时,的值\(a\)将大于的\(b\)值;当长轴垂直时,的值\(b\)将大于的值\(a\)。 我们将使用这些信息绘制以原点为中心的椭圆。
中心椭圆\((0,0)\)
| \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) | \(a>b\) | \(b>a\) |
|---|---|---|
| 长轴 | 在\(x\)-轴上。 | 在\(y\)-轴上 |
| \(x\)-拦截 | \((-a, 0),(a, 0)\) | |
| \(y\)-拦截 | \((0,-b),(0, b)\) |
图表:\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)。
解决方案:
| 第 1 步。 用标准形式写出方程式。 | 它是标准形式。 | \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) |
| 第 2 步。 确定长轴是水平还是垂直。 | 由于\(9>4\)和\(9\)在\(y^{2}\)术语中,长轴是垂直的。 | 长轴是垂直的。 |
| 第 3 步。 找到长轴的端点。 |
端点将是\(y\)-intercepts。 从\(b^{2}=9\)那以后\(b=\pm 3\)。 长轴的端点是\((0,3),(0,-3)\)。 |
长轴的端点是\((0,3),(0,-3)\)。 |
| 第 4 步。 找到短轴的端点。 | 端点将是\(x\)-intercepts。
从\(a^{2}=4\)那以后\(a=\pm 2\)。 长轴的端点是\((2,0),(-2,0)\)。 |
长轴的端点是\((2,0),(-2,0)\)。 |
| 第 5 步。 草绘椭圆。 | .png) |
图表:\(\frac{x^{2}}{4}+\frac{y^{2}}{16}=1\)。
- 回答
-
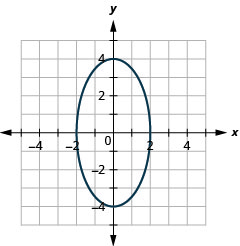
图 11.3.7
图表:\(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)。
- 回答
-
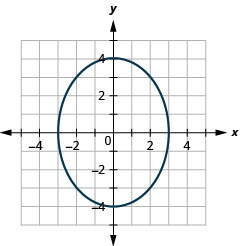
图 11.3.8
我们总结了这些步骤以供参考。
如何绘制中心椭圆\((0,0)\)。
- 用标准形式写出方程式。
- 确定长轴是水平还是垂直。
- 找到长轴的端点。
- 找到短轴的端点
- 草绘椭圆。
有时我们的方程首先需要采用标准形式。
图表\(x^{2}+4 y^{2}=16\)。
解决方案:
| 我们将其视为 椭圆方程,因为\(x\)和\(y\)项都是 平方且系数不同。 |
\(x^{2}+4 y^{2}=16\) |
| 要获得标准形式的方程,请将 两边除 以\(16\)使方程等于\(1\)。 |
\(\frac{x^{2}}{16}+\frac{4 y^{2}}{16}=\frac{16}{16}\) |
| 简化。 | \(\frac{x^{2}}{16}+\frac{y^{2}}{4}=1\) |
| 方程为标准形式。 椭圆以原点为中心。 |
中心是\((0,0)\)。 |
| 由于\(16>4\)和\(16\)在\(x^{2}\)术语 中,长轴是水平的。 |
|
| \(a^{2}=16, a=\pm 4\) \(b^{2}=4, \quad b=\pm 2\) |
顶点是\((4,0),(−4,0)\)。 短轴的端点是 \((0,2),(0,−2)\)。 |
| 绘制抛物线。 | 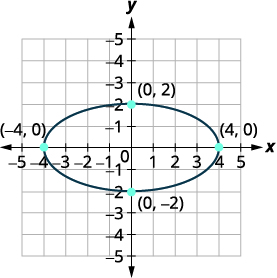 |
图表\(9 x^{2}+16 y^{2}=144\)。
- 回答
-
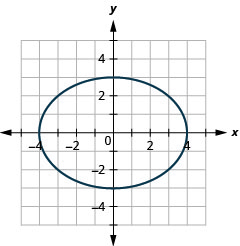
图 11.3.10
图表\(16 x^{2}+25 y^{2}=400\)。
- 回答
-
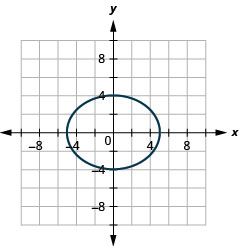
图 11.3.11
求以原点为中心的椭圆方程
如果给我们一个椭圆的图形,我们就能找到椭圆的方程。
找到所示椭圆的方程。
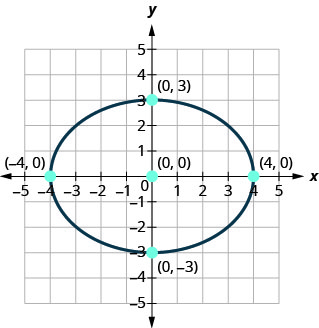
解决方案:
我们认为这是一个以原点为中心的椭圆。
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
既然长轴是水平的,从中心到顶点的距离是水平的\(4\),我们知道\(a=4\)等等\(a^{2}=16\)。
\(\frac{x^{2}}{16}+\frac{y^{2}}{b^{2}}=1\)
我们知道\(b=3\),短轴是垂直的,从中心到椭圆的距离是垂直的\(3\),依此类推\(b^{2}=9\)。
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
找到所示椭圆的方程。
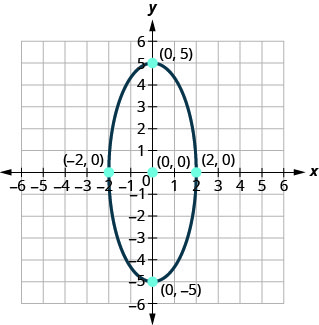
- 回答
-
\(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
找到所示椭圆的方程。
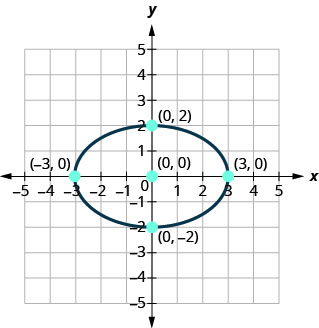
- 回答
-
\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)
绘制中心不在原点的椭圆
到目前为止,我们看到的椭圆都以原点为中心。 现在我们来看中心为的椭圆\((h,k)\)。
方程为\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\),何时\(a>b\),长轴是水平的,所以从中心到顶点的距离是\(a\)。 当时\(b>a\),长轴是垂直的,因此从中心到顶点的距离是\(b\)。
方程的标准形式是中心椭圆\((h,k)\)
中心\((h,k)\)椭圆方程的标准形式是
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
当时\(a>b\),长轴是水平的,所以从中心到顶点的距离是\(a\)。
当时\(b>a\),长轴是垂直的,因此从中心到顶点的距离是\(b\)。
图表:\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\)。
解决方案:
| 方程采用标准形式,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)。 | \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) |
| 椭圆的中心位于\((h,k)\)。 | 中心是\((3,1)\)。 |
| 由于\(9>4\)和\(9\)在\(x^{2}\)术语中,长轴是水平的。 | |
| \(a^{2}=9, a=\pm 3\) \(b^{2}=4, b=\pm 2\) |
从中心到顶点的距离为\(3\)。 从短轴中心到端点的 距离为\(2\)。 |
| 草绘椭圆。 | 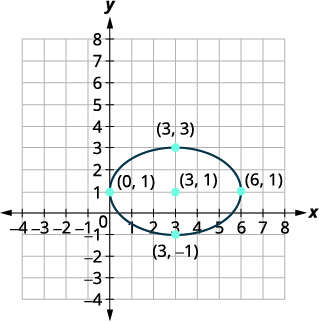 |
图表:\(\frac{(x+3)^{2}}{4}+\frac{(y-5)^{2}}{16}=1\)。
- 回答
-
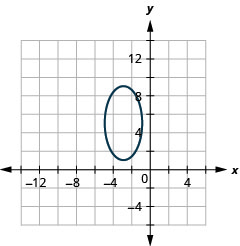
图 11.3.16
图表:\(\frac{(x-1)^{2}}{25}+\frac{(y+3)^{2}}{16}=1\)。
- 回答
-
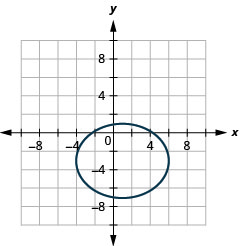
图 11.3.17
如果我们看一下\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)和的方程\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\),就会发现它们都是带有\(a=3\)和的椭圆\(b=2\)。 因此,它们将具有相同的大小和形状。 它们的不同之处在于它们没有相同的中心。
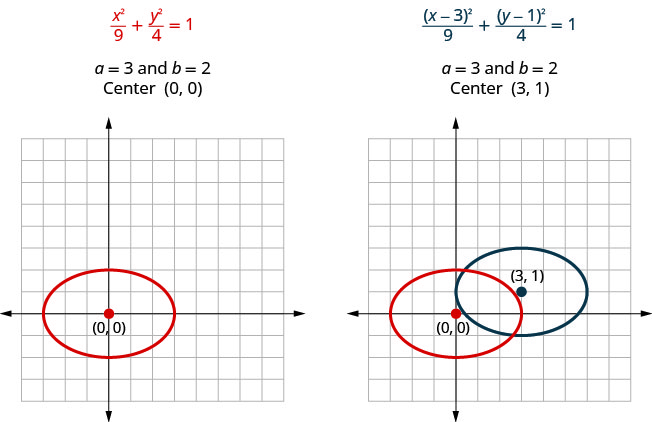
请注意,在上面的图表中,我们可以\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\)通过翻译来绘制图表。 我们将原来的椭圆向右\(3\)移动,然后向上移动\(1\)单位。
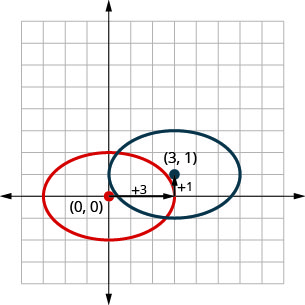
在下一个示例中,我们将使用平移方法绘制椭圆的图形。
\(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\)按翻译绘制图表。
解决方案:
这个椭圆的大小和形状将与中心\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)所在的椭圆相同\((0,0)\)。 我们先绘制这个椭圆的图。
| 中心是\((0,0)\)。 | 中心\((0,0)\) |
| 因为\(16>9\),长轴是水平的。 | |
| \(a^{2}=16, a=\pm 4\) \(b^{2}=9, \quad b=\pm 3\) |
顶点是\((4,0),(−4,0)\)。 短轴的端点是 \((0,3),(0,−3)\)。 |
| 草绘椭圆。 | 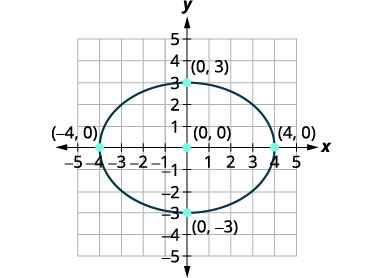 |
| 原始方程为标准形式,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)。 | \(\frac{(x-(-4))^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) |
| 椭圆的中心位于\((h,k)\)。 | 中心是\((-4,6)\)。 |
| 我们将\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)四个 单位的图形向左平移,然后向上转换\(6\)单位。 验证中心是否为\((−4,6)\)。 新椭圆是方程 为的椭圆 \(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\)。 |
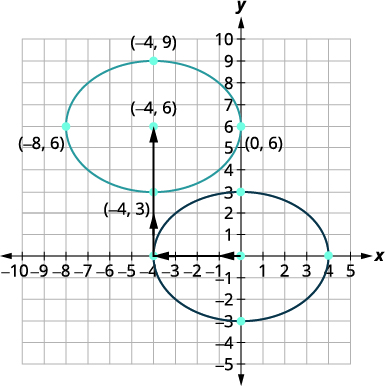 |
\(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{4}=1\)按翻译绘制图表。
- 回答
-
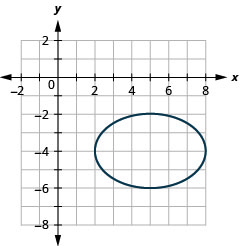
图 11.3.22
\(\frac{(x+6)^{2}}{16}+\frac{(y+2)^{2}}{25}=1\)按翻译绘制图表。
- 回答
-
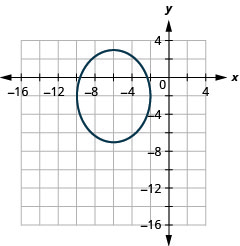
图 11.3.23
当一个方程的系数不同的 a\(x^{2}\) 和 a\(y^{2}\) 时,我们通过将其置于标准形式来验证它是否为省略号。 然后,我们将能够绘制方程式。
用标准\(x^{2}+4 y^{2}-4 x+24 y+24=0\)形式和图表写下方程。
解决方案:
我们通过填写\(x\)和中的正方形将方程置于标准形式\(y\)。
| \(x^{2}+4 y^{2}-4 x+24 y+24=0\) | |
| 重写\(x\)术语和\(y\)术语的分组。 | 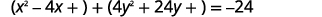 |
| 使\(x^{2}\)和的系数\(y^{2}\)相等\(1\)。 | 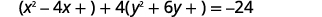 |
| 完成方格。 | 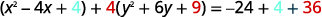 |
| 写成二项式方块。 | 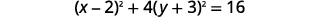 |
| 将两边除\(16\)以向\(1\)右移动。 | 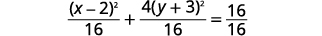 |
| 简化。 | 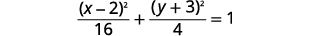 |
| 方程采用标准形式,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) | 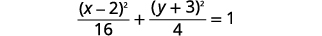 |
| 椭圆的中心位于\((h,k)\)。 | 中心是\((2,-3)\)。 |
|
由于\(16>4\)和\(16\)在\(x^{2}\)术语中,长轴是水平的。 \(a^{2}=16, a=\pm 4\) |
从中心到顶点的距离为\(4\)。 从短轴中心到端点的距离为\(2\)。 |
| 草绘椭圆。 | 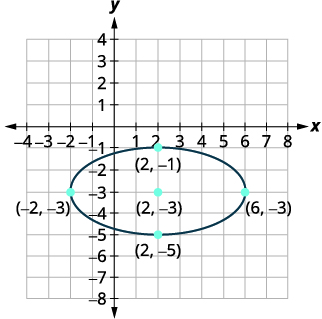 |
- 用标准形式写\(6 x^{2}+4 y^{2}+12 x-32 y+34=0\)下方程式然后
- 图表。
- 回答
-
- \(\frac{(x+1)^{2}}{6}+\frac{(y-4)^{2}}{9}=1\)
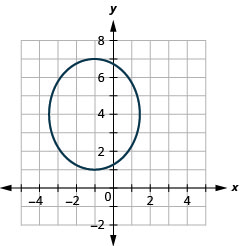
图 11.3.32
- 用标准形式写\(4 x^{2}+y^{2}-16 x-6 y+9=0\)下方程式然后
- 图表。
- 回答
-
- \(\frac{(x-2)^{2}}{4}+\frac{(y-3)^{2}}{16}=1\)
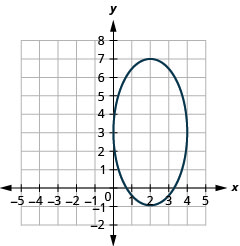
图 11.3.33
用省略号求解应用程序
行星绕太阳的轨道遵循椭圆形路径。
冥王星(一颗矮行星)在绕太阳的椭圆轨道上移动。 冥王星离太阳最近的距离大约是\(30\)天文单位(AU),最远的约为\(50\) AU。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标注轴,轨道将如下图所示。 使用图表为冥王星的椭圆轨道写一个方程。
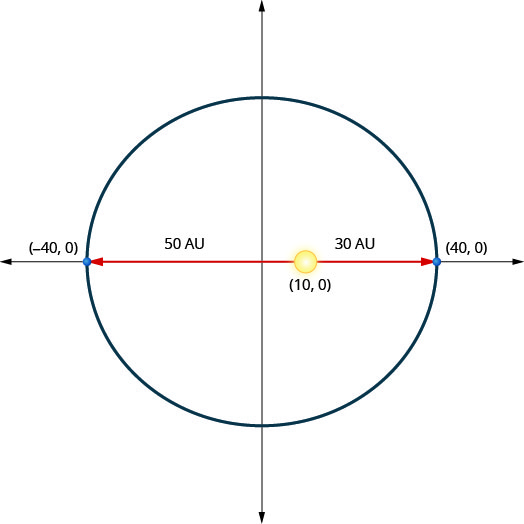
解决方案:
我们认为这是一个以原点为中心的椭圆。
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
既然长轴是水平的,从中心到顶点的距离是水平的\(40\),我们知道\(a=40\)等等\(a^{2}=1600\)。
\(\frac{x^{2}}{1600}+\frac{y^{2}}{b^{2}}=1\)
短轴是垂直的,但没有给出终点。要找到,\(b\)我们将使用太阳的位置。 既然太阳是椭圆在该点的焦点\((10,0)\),我们知道\(c=10\)。 用这个来求解\(b^{2}\)。
\(b^{2}=a^{2}-c^{2}\)
\(b^{2}=40^{2}-10^{2}\)
\(b^{2}=1600-100\)
\(b^{2}=1500\)
\(b^{2}\)将\(a^{2}\)和替换为椭圆的标准形式。
\(\frac{x^{2}}{1600}+\frac{y^{2}}{1500}=1\)
一颗行星在绕太阳的椭圆轨道上移动。 行星离太阳最近的距离大约是\(20\)非盟,最远的距离大约是\(30\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标注轴,轨道将如下图所示。 使用图表为行星的椭圆轨道写一个方程。
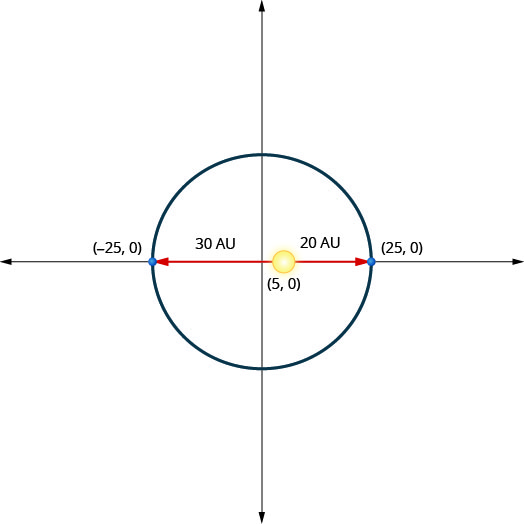
- 回答
-
\(\frac{x^{2}}{625}+\frac{y^{2}}{600}=1\)
一颗行星在绕太阳的椭圆轨道上移动。 行星离太阳最近的距离大约是\(20\)非盟,最远的距离大约是\(50\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标注轴,轨道将如下图所示。 使用图表为行星的椭圆轨道写一个方程。
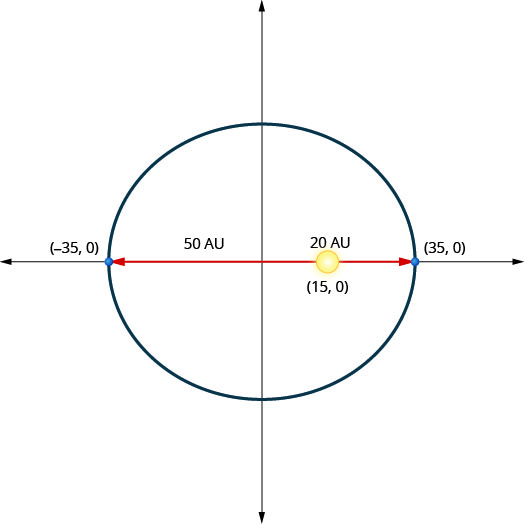
- 回答
-
\(\frac{x^{2}}{1225}+\frac{y^{2}}{1000}=1\)
访问这些在线资源以获取更多说明和使用省略号进行练习。
- 圆锥截面:绘制椭圆图第 1 部分
- 圆锥截面:绘制椭圆图第 2 部分
- 来自图表的椭圆方程
关键概念
- 椭圆:椭圆是平面中的所有点,其中两个定点的距离之和是恒定的。 每个定点都称为椭圆的焦点。
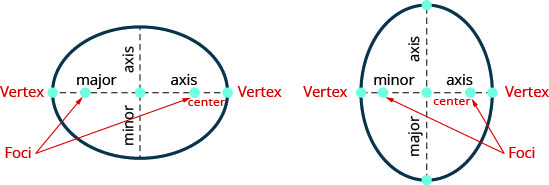
图 11.3.37
- 如果我们画一条穿过焦点的直线,则椭圆在两个点上相交——每个点都被称为椭圆的顶点。
连接顶点的线段称为长轴。
线段的中点称为椭圆的中心。
垂直于长轴、穿过中心并在两点上与椭圆相交的线段称为短轴。 - 方程的标准形式带中心的椭圆\((0,0)\):中心椭圆方程的标准形式是\((0,0)\)
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
\(x\)-intercepts 是\((a,0)\)和\((−a,0)\)。
\(y\)-intercepts 是\((0,b)\)和\((0,−b)\)。 - 如何画一个中间的椭圆\((0,0)\)
- 用标准形式写出方程式。
- 确定长轴是水平还是垂直。
- 找到长轴的端点。
- 找到短轴的端点
- 草绘椭圆。
- 方程的标准形式带中心的椭圆\((h,k)\):中心椭圆方程的标准形式是\((h,k)\)
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
当时\(a>b\),长轴是水平的,所以从中心到顶点的距离是\(a\)。
当时\(b>a\),长轴是垂直的,因此从中心到顶点的距离是\(b\)。
词汇表
- 椭圆
- 椭圆是平面中的所有点,其中两个定点的距离之和是恒定的。


