Skip to main content
Global

11.4E：练习

  1. Last updated
  2. Save as PDF
  • Page ID
    204450

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    练习成就完美

    练习\(\PageIndex{15}\) Graph an Ellipse with Center at the Origin

    在以下练习中，绘制每个椭圆的图形。

    1. \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    3. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    4. \(\frac{x^{2}}{16}+\frac{y^{2}}{36}=1\)
    5. \(\frac{x^{2}}{36}+\frac{y^{2}}{16}=1\)
    6. \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
    7. \(x^{2}+\frac{y^{2}}{4}=1\)
    8. \(\frac{x^{2}}{9}+y^{2}=1\)
    9. \(4 x^{2}+25 y^{2}=100\)
    10. \(16 x^{2}+9 y^{2}=144\)
    11. \(16 x^{2}+36 y^{2}=576\)
    12. \(9 x^{2}+25 y^{2}=225\)
    回答

    1。

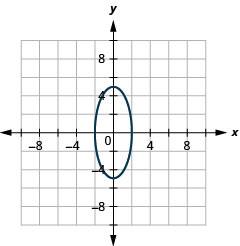
    此图显示了一个椭圆，其中心为 (0, 0)，顶点 (0, 5) 和 (0，负 5)，端点为短轴 (2, 0) 和 (负 2, 0)。
    图 11.3.38

    3。

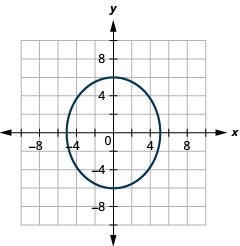
    此图显示了一个椭圆，其中心为 (0, 0)，顶点 (0, 6) 和 (0，负 6)，端点为短轴 (5, 0) 和 (负 5, 0)。
    图 11.3.39

    5。

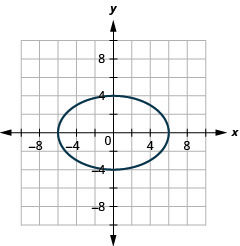
    此图显示了一个椭圆，其中心为 (0, 0)、顶点 (6、0) 和（负 6、0），端点为短轴（0、4）和（0，负 4）。
    图 11.3.40

    7。

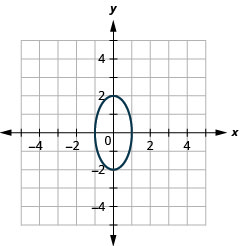
    此图显示了一个椭圆，其中心为 (0, 0)，顶点 (0, 2) 和 (0，负 2)，端点为短轴 (1, 0) 和 (负 1, 0)。
    图 11.3.41

    9。

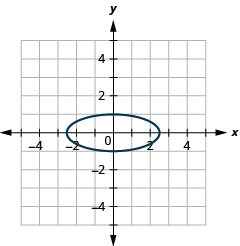
    此图显示了中心点 (0, 0)、顶点 (5, 0) 和 (负 5, 0) 以及端点为短轴 (0, 2) 和 (0, 负 2) 的椭圆。
    图 11.3.42

    11。

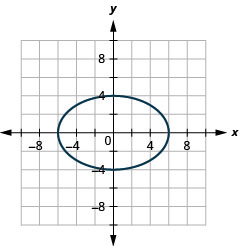
    此图显示了一个椭圆，其中心为 (0, 0)、顶点 (6、0) 和（负 6、0），端点为短轴（0、4）和（0，负 4）。
    图 11.3.43
    练习\(\PageIndex{16}\) Find the Equation of an Ellipse with Center at the Origin

    在以下练习中，找到图中显示的椭圆的方程。

    1。

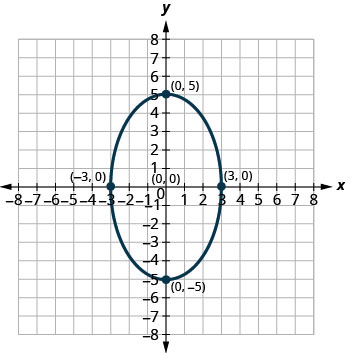
    此图显示了一个椭圆，其中心 (0, 0)、顶点 (0、5) 和 (0，负 5) 以及短轴 (负 3, 0) 和 (3, 0) 的端点。
    图 11.3.44

    2。

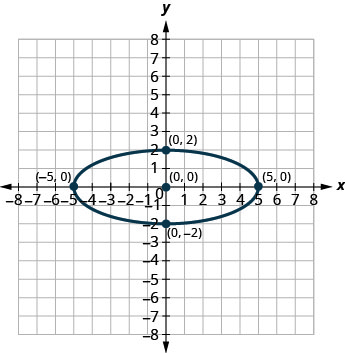
    此图显示了中心点 (0, 0)、顶点 (5, 0) 和 (负 5, 0) 以及端点为短轴 (0, 2) 和 (0, 负 2) 的椭圆。
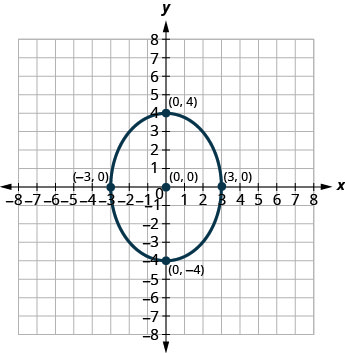
    图 11.3.45

    3。

    此图显示了一个椭圆，其中心 (0, 0)、顶点 (0、4) 和 (0，负 4) 以及短轴 (负 3, 0) 和 (3, 0) 的端点。
    图 11.3.46

    4。

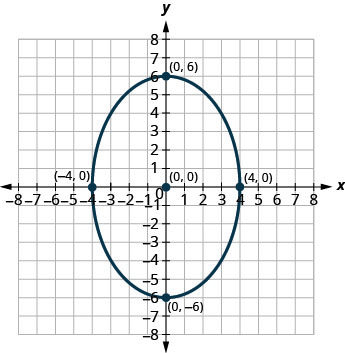
    此图显示了一个椭圆，其中心为 (0, 0)，顶点 (0, 6) 和 (0，负 6)，端点为短轴 (负 4, 0) 和 (4, 0)。
    图 11.3.47
    回答

    1。 \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)

    3。 \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)

    练习\(\PageIndex{17}\) Graph an Ellipse with Center Not at the Origin

    在以下练习中，绘制每个椭圆的图形。

    1. \(\frac{(x+1)^{2}}{4}+\frac{(y+6)^{2}}{25}=1\)
    2. \(\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1\)
    3. \(\frac{(x+4)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
    4. \(\frac{(x-4)^{2}}{9}+\frac{(y-1)^{2}}{16}=1\)
    回答

    1。

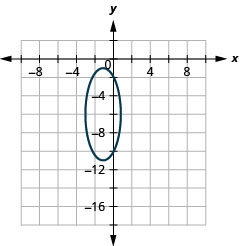
    此图显示了中心点（负 1、负 6）、顶点（负 1、负 1）和（负 1、负 11）以及端点为短轴（负 3、负 6）和（1，负 6）的椭圆。
    图 11.3.48

    3。

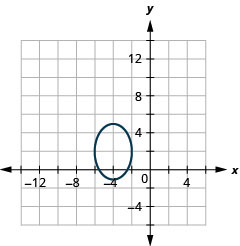
    此图显示了一个椭圆，其中心为负 4、2、顶点（负 4、5）和（负 4，负 1），端点为短轴（3、1）和（负 6、2）和（负 2、2）。
    图 11.3.49
    练习\(\PageIndex{18}\) Graph an Ellipse with Center Not at the Origin

    在以下练习中，用平移绘制每个方程的图形。

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
    2. \(\frac{(x+6)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
    3. \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{25}=1\)
    4. \(\frac{(x+5)^{2}}{36}+\frac{(y-3)^{2}}{16}=1\)
    回答

    1。

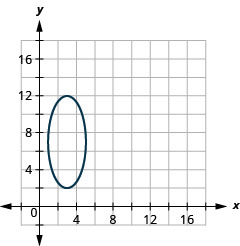
    此图显示了一个椭圆，其中心为 (3、7)、顶点 (3、2) 和 (3、12)，端点为短轴 (1、7) 和 (5、7)。
    图 11.3.50

    3。

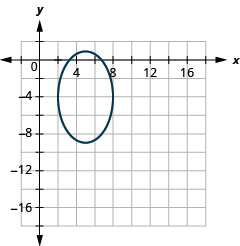
    此图显示了一个椭圆，其中心（5，负 4）、顶点（5、1）和（5，负 9），端点为短轴（2，负 4）和（8，负 4）。
    图 11.3.51
    练习\(\PageIndex{19}\) Graph an Ellipse with Center Not at the Origin

    在以下练习中，

    1. 用标准形式写下方程式然后
    2. 图表。
    1. \(25 x^{2}+9 y^{2}-100 x-54 y-44=0\)
    2. \(4 x^{2}+25 y^{2}+8 x+100 y+4=0\)
    3. \(4 x^{2}+25 y^{2}-24 x-64=0\)
    4. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    回答

    1。

    1. \(\frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{25}=1\)
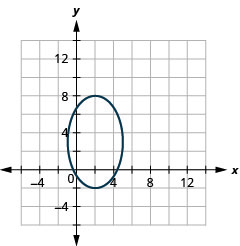
    此图显示了一个椭圆，其中心为中心 (2, 3)，顶点 (2，负 2) 和 (2, 8)，端点为短轴 (负 1, 3) 和 (5, 3)。
    图 11.3.52

    3。

    1. \(\frac{y^{2}}{4}+\frac{(x-3)^{2}}{25}=1\)
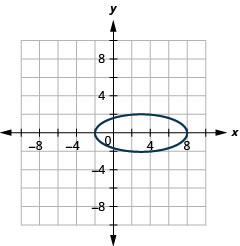
    此图显示了一个椭圆，其中心为 (3, 0)、顶点（负 2、0）和（8、0），端点为短轴（3、2）和（3，负 2）。
    图 11.3.53
    练习\(\PageIndex{20}\) Graph an Ellipse with Center Not at the Origin

    在以下练习中，绘制方程的图表。

    1. \(x=-2(y-1)^{2}+2\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \(y=-x^{2}+8 x-15\)
    5. \(\frac{(x+3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\)
    6. \((x-2)^{2}+(y-3)^{2}=9\)
    7. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    8. \(x=4(y+1)^{2}-4\)
    9. \(x^{2}+y^{2}=64\)
    10. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    11. \(y=6 x^{2}+2 x-1\)
    12. \(\frac{(x-2)^{2}}{9}+\frac{(y+3)^{2}}{25}=1\)
    回答

    1。

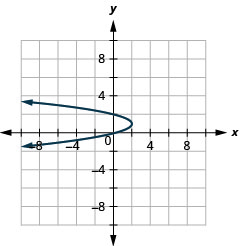
    此图显示了一个带有顶点 (2, 1) 和 y 截距 (0, 0) 和 (2, 0) 的抛物线。
    图 11.3.54

    3。

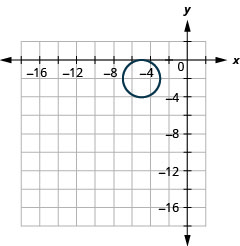
    此图显示了一个中心（负 5，负 2）、半径为 2 个单位的圆。
    图 11.3.55

    5。

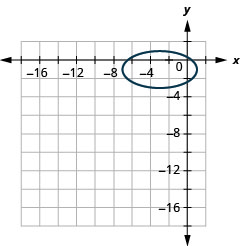
    此图显示了一个具有中心（负 3、负 1）、顶点（1、负 1）和（负 7、负 1）的椭圆，以及短轴（负 3、负 3）和（负 3、负 3）的端点。
    图 11.3.56

    7。

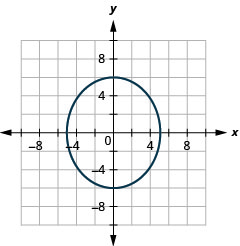
    此图显示了一个椭圆，其中心为 (0, 0)，顶点 (0, 6) 和 (0，负 6)，端点为短轴 (负 5, 0) 和 (5, 0)。
    图 11.3.57

    9。

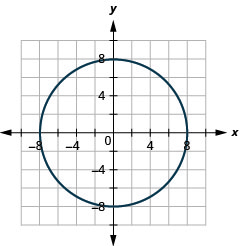
    此图显示了中心为 (0, 0) 且半径为 8 单位的圆。
    图 11.3.58

    11。

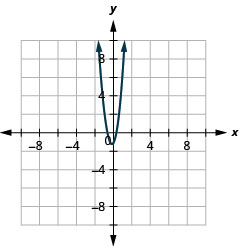
    这张图显示了向上开放的抛物线。 其顶点的 x 值略小于 0，y 值略小于负 1。 其上的一个点大约在（负 1, 3）处。
    图 11.3.59
    练习\(\PageIndex{21}\) Solve Application with Ellipses

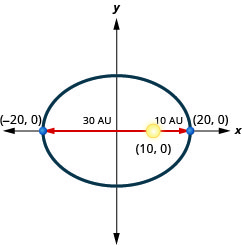
    1。 一颗行星在绕太阳的椭圆轨道上移动。 行星离太阳最近的距离大约是\(10\)非盟，最远的距离大约是\(30\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标记轴，轨道将如下图所示。 使用图表为行星的椭圆轨道写一个方程。

    此图显示了一个具有中心 (0, 0)、顶点 (负 20, 0) 和 (20, 0) 的椭圆。 太阳显示在点 (10, 0) 处，该点距左顶点 30 个单位，距右顶点 10 个单位。
    图 11.3.60

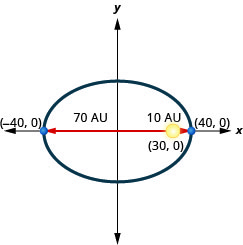
    2。 一颗行星在绕太阳的椭圆轨道上移动。 行星离太阳最近的距离大约是\(10\)非盟，最远的距离大约是\(70\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标记轴，轨道将如下图所示。 使用图表为行星的椭圆轨道写一个方程。

    此图显示了一个具有中心 (0, 0)、顶点 (负 40, 0) 和 (40, 0) 的椭圆。 太阳显示在点 (30, 0) 处，该点距左顶点 70 个单位，距右顶点 10 个单位。
    图 11.3.61

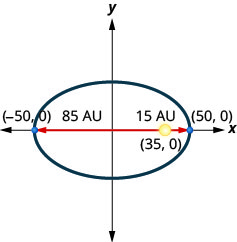
    3。 一颗彗星围绕太阳在椭圆轨道上移动。 彗星离太阳最近的距离大约是\(15\)非盟，最远的距离大约是\(85\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标记轴，轨道将如下图所示。 使用图表为彗星的椭圆轨道写出方程。

    此图显示了一个具有中心 (0, 0)、顶点 (负 50, 0) 和 (50, 0) 的椭圆。 太阳显示在点 (35, 0) 处，即距左顶点 85 个单位，距右顶点 15 个单位。
    图 11.3.62

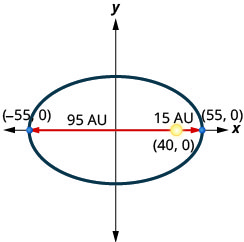
    4。 一颗彗星围绕太阳在椭圆轨道上移动。 彗星离太阳最近的距离大约是\(15\)非盟，最远的距离大约是\(95\)非盟。 太阳是椭圆轨道的焦点之一。 让椭圆以原点为中心并在 AU 中标记轴，轨道将如下图所示。 使用图表为彗星的椭圆轨道写出方程。

    此图显示了一个具有中心 (0, 0)、顶点 (负 55、0) 和 (55, 0) 的椭圆。 太阳显示在点 (40, 0) 处，即距左顶点 95 个单位，距右顶点 15 个单位。
    图 11.3.63
    回答

    1。 \(\frac{x^{2}}{400}+\frac{y^{2}}{300}=1\)

    3。 \(\frac{x^{2}}{2500}+\frac{y^{2}}{1275}=1\)

    练习\(\PageIndex{22}\) Writing Exercises
    1. 用你自己的话说，定义一个椭圆，然后用标准形式写出以原点为中心的椭圆的方程。 绘制椭圆草图，标注中心、顶点以及长轴和短轴。
    2. 用你自己的话解释如何以标准形式从方程中获得轴。
    3. 比较和对比方程图\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)和\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\).
    4. 用你自己的话解释椭圆顶点和焦点之间的区别。
    回答

    1。 答案可能有所不同

    3。 答案可能有所不同

    自检

    a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

    此表有 4 列 4 行和一个标题行。 在一些帮助下，标题行自信地标记了我能做到的每一列，不，我不明白。™ 第一列有以下语句：绘制以原点为中心的椭圆，求出中心位于原点的椭圆的方程，绘制中心不在原点的椭圆，用椭圆求解应用程序。 其余列为空白。
    图 11.3.64

    b. 关于你对本部分的掌握程度，这份清单告诉了你什么？ 你会采取哪些措施来改进？