Skip to main content
Global

11.5: 双曲线

  1. Last updated
  2. Save as PDF
  • Page ID
    204396

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    学习目标

    在本节结束时，您将能够：

    • 绘制一个双曲线，中心位于\((0,0)\)
    • 绘制一个双曲线，中心位于\((h,k)\)
    • 通过圆锥截面的方程识别圆锥截面

    在开始之前，请参加这个准备测验。

    1. 解决：\(x^{2}=12\)。
      如果您错过了此问题，请查看示例 9.1。
    2. 扩展：\((x−4)^{2}\)。
      如果您错过了此问题，请查看示例 5.32。
    3. 图表\(y=-\frac{2}{3} x\)。
      如果你错过了这个问题，请查看示例 3.4。

    绘制一个双曲线图，中心位于\((0,0)\)

    我们要看的最后一个圆锥部分叫做双曲线。 我们将看到双曲线的方程看起来与椭圆方程相同，只是它是差值而不是总和。 虽然椭圆和双曲线的方程非常相似，但它们的图形却大不相同。

    我们将双曲线定义为平面中的所有点，其中它们与两个固定点的距离之差不变。 每个定点都称为双曲线的焦点。

    定义\(\PageIndex{1}\)

    双曲线是平面中的所有点，其与两个固定点的距离之差不变。 每个定点都称为双曲线的焦点。

    该图显示了一个双打磨的右圆锥体，该圆锥被平行于圆锥体垂直轴的平面切成双曲线。 这个人物标有 “hyperbolaမ” 的标签。
    图 11.4.1

    穿过焦点的直线称为横轴。 横轴与双曲线相交的两个点均为双曲线的顶点。 连接焦点的线段的中点称为双曲线的中心。 垂直于穿过中心的横轴的直线称为共轭轴。 图表的每一部分都被称为双曲线的一个分支。

    该图显示了两张双曲线图。 第一张图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 顶点和焦点以位于横轴（即 x 轴）上的点显示。 树枝穿过顶点并左右打开。 y 轴是共轭轴。 第二张图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 顶点和焦点线以位于横轴（即 y 轴）上的点来显示。 树枝穿过顶点并上下开放。 x 轴是共轭轴。
    图 11.4.2

    同样，我们的目标是将圆锥的几何与代数连接起来。 将双曲线放在矩形坐标系上为我们提供了这样的机会。 在图中，我们放置了双曲线，使焦点\(((−c,0),(c,0))\)位于\(x\)-轴上，中心是原点。

    该图显示了双曲线的图形。 该图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 焦点（负 c, 0）和（c, 0）标有点，位于 x 轴上。 顶点用点标记并位于 x 轴上。 树枝穿过顶点并左右打开。 从（负 c，0）到分支（x，y）上某一点的距离被标记为 d sub 1。 从树枝上的 (x, y) 到 (c, 0) 的距离标记为 d sub 2。
    图 11.4.3

    该定义指出，从焦点到点的距离的差异\((x,y)\)是恒定的。 因此\(|d_{1}−d_{2}|\)，我们称之\(2a\)为常数\(|d_{1}-d_{2} |=2 a\)。 我们将使用距离公式来引导我们得出椭圆的代数公式。

    \(\left|d_{1} - d_{2}\right| =2 a\)

    使用距离公式查找\(d_{1}, d_{2}\)

    \(\left|\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}\right|=2 a\)

    消灭激进分子。 为了简化椭圆的方程，我们让\(c^{2}-a^{2}=b^{2}\)。

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{c^{2}-a^{2}}=1\)

    因此，标准形式中以原点为中心的双曲线方程为：

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)

    要绘制双曲线图，了解截获量会很有帮助。 我们将使用公式找到\(x\)-intercepts和\(y\)-intercepts。

    \(x\)-拦截

    让\(y=0\)。

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)

    \(x\)-intercepts 是\((a,0)\)和\((−a,0)\)。

    \(y\)-拦截

    让\(x=0\)。

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\-\frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=-b^{2} \\ y &=\pm \sqrt{-b^{2}} \end{aligned}\)

    没有\(y\)-intercepts。

    方程中的\(a, b\)值还可以帮助我们找到双曲线的渐近线。 渐近线与图形分支接近的直线相交，但随着\(x, y\)值越来越大，它们永远不会相交。

    为了找到渐近线，我们绘制了一个矩形，其边在顶点处与 x 轴相交\((−a,0),(a,0)\)，在\(y\)-axis 处相交\((0,−b), (0,b)\)。 包含该矩形对角线的线条是双曲线的渐近线。 矩形和渐近线不是双曲线的一部分，但它们可以帮助我们绘制双曲线图。

    该图显示了双曲线的图形。 该图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 顶点为（负 a, 0）和（a, 0），并标有点并位于 x 轴上。 点 (0, b) 和 (0, 负) 位于 y 轴上。 有一个中心矩形，其边在顶点（负 a、0）和（a、0）处与 x 轴相交，在（0，b）和（0，负 b）处与 y 轴相交。 渐近线由 y 等于 b 除以 a 乘以 x 给出，y 等于负 b 除以 a 乘以 x，然后绘制为中心矩形的对角线。 双曲线的分支穿过顶点，左右打开，然后接近渐近线。
    图 11.4.4

    渐近线穿过原点，我们可以使用我们绘制的矩形来评估它们的斜率。 它们有方程\(y=\frac{b}{a} x\)和\(y=-\frac{b}{a} x\).

    双曲线有两个方程，这取决于横轴是垂直还是水平。 我们可以通过查看方程来判断横轴是否是水平的。 当方程为标准形式时，如果\(x^{2}\)-term 为正，则横轴为水平。 当方程为标准形式时，如果\(y^{2}\)-term 为正，则横轴为垂直。

    第二个方程可以像我们所做的那样得出。 我们将在这里总结结果。

    定义\(\PageIndex{2}\)

    方程的标准形式是带中心的双曲线\((0,0)\)

    中心\((0,0)\)双曲线方程的标准形式是

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad\)或者\(\quad \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)

    该图显示了两个双曲线的图形。 第一张图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 顶点为（负 a, 0）和（a, 0），并标有点并位于 x 轴上。 点 (0, b) 和 (0, 负) 位于 y 轴上。 有一个中心矩形，其边在顶点（负 a、0）和（a、0）处与 x 轴相交，在（0，b）和（0，负 b）处与 y 轴相交。 渐近线由 y 等于 b 除以 a 乘以 x 给出，y 等于负 b 除以 a 乘以 x，然后绘制为中心矩形的对角线。 双曲线的分支穿过顶点，左右打开，然后接近渐近线。 第二张图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 顶点为 (0, a) 和 (0, 负 a)，并标有点并位于 y 轴上。 点 (0, b) 和 (0, 负) 位于 y 轴上。 有一个中心矩形，其边在顶点（0，a）和（0，负 a）处与 y 轴相交，在（负 b，0）和（b，0）处与 y 轴相交。 双曲线的分支穿过顶点，上下打开，然后接近渐近线。
    图 11.4.5

    请注意，与椭圆方程不同，的分母\(x^{2}\)并不总是如此\(a^{2}\)，分母也不\(y^{2}\)总是如此\(b^{2}\)。

    请注意，当\(x^{2}\)-term 为正时，横轴位于\(x\)-axis 上。 当\(y^{2}\)-term 为正值时，横轴位于\(y\)-axis 上。

    方程的标准形式是带中心的双曲线\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    方向 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\(x\)-axis 上的横轴。
    左右打开    		 \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\(y\)-axis 上的横轴。
    向上和向下打开
    顶点 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\((0,-a),(0, a)\)
    \(x\)-拦截 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >无
    \(y\)-拦截 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >无 \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\((0,-a),(0, a)\)
    矩形 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >使用\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >使用\((0, \pm a)( \pm b, 0)\)
    渐近线 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    表 11.4.1

    我们将使用这些属性来绘制双曲线图。

    示例\(\PageIndex{1}\) How to Graph a Hyperbola with Center \((0,0)\)

    图表\(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\)。

    解决方案：

    第 1 步：以标准形式写出方程式。 方程为标准形式。 \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\)
    步骤 2：确定横轴是水平还是垂直。 由于\(x^{2}\)-term 为正，因此横轴是水平的。 横轴是水平的。
    步骤 3：找到顶点。 从\(a^{2}=25\)那以后\(a=\pm 5\)。 顶点在\(x\)-axis 上。 \((-5,0),(5,0)\)
    第 4 步：绘制以原点交叉点为中心的矩形\(\pm a\)，一个轴位于另一个轴处\(\pm b\)。

    因为\(a=\pm 5\)，矩形将在顶点处与\(x\)-轴相交。

    因为\(b=\pm 2\)，矩形将在\((0,-2)\)和处与\(y\)-轴相交\((0,2)\)。

    		 屏幕截图 (148) .png

    第 5 步：绘制渐近线——穿过矩形对角线的直线。

    		 渐近线有方程\(y=\frac{5}{2} x, y=-\frac{5}{2} x\)。 屏幕截图 (149) .png
    步骤 6：画出双曲线的两个分支。 从每个顶点开始，使用渐近线作为指导。 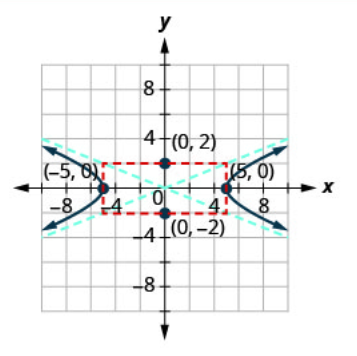屏幕截图 (150) .png
    表 11.4.2
    练习\(\PageIndex{1}\)

    图表\(\frac{x^{2}}{16}-\frac{y^{2}}{4}=1\)。

    回答
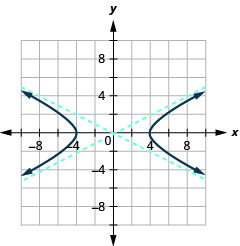
    该图显示了 x 轴和 y 轴，它们均沿负向和正方向延伸，但间隔未标记，渐近线 y 等于正负乘以 x 的一半，分支穿过顶点（正负 4，0）并左右打开。
    图 11.4.9
    练习\(\PageIndex{2}\)

    图表\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\)。

    回答
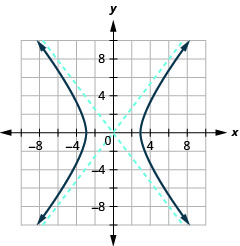
    该图显示了 x 轴和 y 轴，它们均沿负向和正方向延伸，但间隔未标记，渐近线 y 等于正负三分之四乘以 x，分支穿过顶点（正负 3，0），然后左右打开。
    图 11.4.10

    我们总结了这些步骤以供参考。

    绘制以双曲线为中心的图形\((0,0)\)

    1. 用标准形式写出方程式。
    2. 确定横轴是水平还是垂直。
    3. 找到顶点。
    4. 绘制以原点为中心的矩形，其中一个轴\(±a\)与另一个轴相交\(±b\)。
    5. 绘制渐近线——穿过矩形对角线的直线。
    6. 画出双曲线的两个分支。

    有时候，在我们绘制双曲线图之前，需要先以标准形式放置双曲线的方程。

    示例\(\PageIndex{2}\)

    图表\(4 y^{2}-16 x^{2}=64\)。

    解决方案：

      \(4 y^{2}-16 x^{2}=64\)
    要以标准形式书写方程，请将每个项除\(64\)以使方程等于\(1\)。 \(\frac{4 y^{2}}{64}-\frac{16 x^{2}}{64}=\frac{64}{64}\)
    简化。 \(\frac{y^{2}}{16}-\frac{x^{2}}{4}=1\)
    由于\(y^{2}\)-term 为正，因此横轴是垂直的。 从\(a^{2}=16\)那以后\(a=\pm 4\)。  
    顶点在\(y\)-axis 上，\((0,-a),(0, a)\)。 从\(b^{2}=4\)那以后\(b=\pm 2\)。 \((0,-4),(0,4)\)
    绘制与\(x\)-axis 相交的矩形，在\((-2,0),(2,0)\)顶点处与\(y\)-axis 相交的矩形。 通过矩形的对角线绘制渐近线。 画出双曲线的两个分支。 。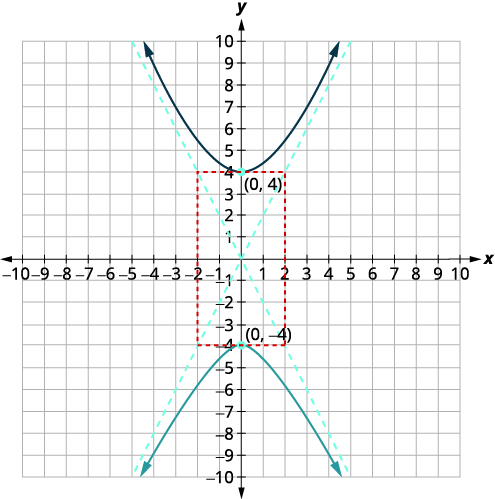
    表 11.4.3
    练习\(\PageIndex{3}\)

    图表\(4 y^{2}-25 x^{2}=100\)。

    回答
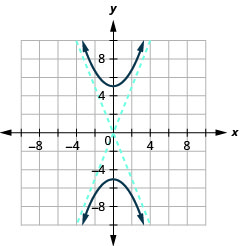
    该图显示了 x 轴和 y 轴，它们均沿负向和正方向延伸，但间隔未标记，渐近线 y 等于正负五半乘以 x，分支穿过顶点（0、正负 5）并上下打开。
    图 11.4.12
    练习\(\PageIndex{4}\)

    图表\(25 y^{2}-9 x^{2}=225\)。

    回答
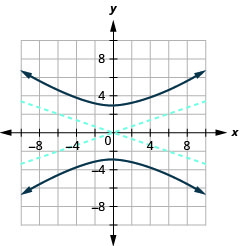
    该图显示了 x 轴和 y 轴，它们均沿负向和正方向延伸，但间隔未标记，渐近线 y 等于正负五分之三乘以 x，分支穿过顶点（0、正负 3）并上下开放。
    图 11.4.13

    绘制一个双曲线图，中心位于\((h,k)\)

    双曲线并不总是以原点为中心。 当双曲线居中时\((h,k)\)，方程会稍有变化，如表中所示。

    方程的标准形式是带中心的双曲线\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    方向 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\) “>横轴是水平的。 左右打开 \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\) “>横轴是垂直的。 向上和向下打开
    中心 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\)” >\((h,k)\) \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\)” >\((h,k)\)
    顶点 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\)” > 中心左侧和右侧的\(a\)单位 \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\)” > 中心上方和下方的\(a\)单位
    矩形 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\) “>在中心上方/下方使用中心\(a\)\(b\)单位左/右的单位 \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\)” >使用中心\(a\)单位上方/下方中心左侧/右侧的\(b\)单位
    表 11.4.4
    示例\(\PageIndex{3}\) How to Graph a Hyperbola with Center \((h,k)\)

    图表\(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)

    解决方案：

    第 1 步：以标准形式写出方程式。 方程为标准形式。 \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)
    步骤 2：确定横轴是水平还是垂直。 由于\(x^{2}\)-term 为正，因此双曲线左右打开。 横轴是水平的。 双曲线左右打开。
    步骤 3: 找到中心然后\(a, b\). \(h=1\)和\(k=2\)
    \(a^{2}=9\)
    \(b^{2}=16\)

    \(\begin{array} {c} \frac{\left(\stackrel{\color{red}{x-h}}{\color{black}{x-1}} \right)^{2}}{9} - \frac{\left(\stackrel{\color{red}{y-k}}{\color{black}{y-2}} \right)^{2}}{16} = 1 \end{array}\)

    中心：\((1,2)\)

    \(a=3\)

    \(b=4\)
    第 4 步：绘制以\((h,k)\)使用为中心的矩形\(a,b\)。

    标记中心，\((1,2)\)。

    绘制一个矩形，该矩形穿过中心左侧/右侧的点\(3\)\(4\)单位以及中心上方和下方的单位。

    		 屏幕截图 (151) .png
    第 5 步：绘制渐近线——穿过矩形对角线的直线。 标记顶点。 绘制对角线。 标记顶点，这些顶点位于中心左侧和右侧的矩形\(3\)单位上。 屏幕截图 (152) .png
    步骤 6：画出双曲线的两个分支。 从每个顶点开始，使用渐近线作为指导。 屏幕截图 (153) .png
    表 11.4.5
    练习\(\PageIndex{5}\)

    图表\(\frac{(x-3)^{2}}{25}-\frac{(y-1)^{2}}{9}=1\)。

    回答
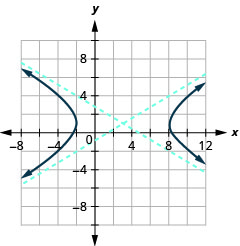
    该图显示了沿负向和正方向延伸但间隔未标记的 x 轴和 y 轴，其渐近线穿过（负 2、负 2）和（8、4），渐近线穿过（负 2、4）和（8，负 2），分支穿过顶点（负 2，负 2）负 2、2）和（8、2），然后左右打开。
    图 11.4.17
    练习\(\PageIndex{6}\)

    图表\(\frac{(x-2)^{2}}{4}-\frac{(y-2)^{2}}{9}=1\)。

    回答
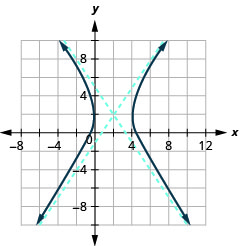
    该图显示了沿负向和正方向延伸但间隔未标记的 x 轴和 y 轴，其中心为（2、2）、穿过（0、负 1）和（4、5）的渐近线和穿过（0、5）和（4，负 1）的渐近线以及穿过顶点的分支(0, 2) 和 (4, 2)，然后左右打开。
    图 11.4.18

    我们总结了这些步骤以便于参考。

    绘制以双曲线为中心的图形\((h,k)\)

    1. 用标准形式写出方程式。
    2. 确定横轴是水平还是垂直。
    3. 找到中心然后\(a,b\).
    4. 绘制以\((h,k)\)使用为中心的矩形\(a,b\)。
    5. 绘制渐近线——穿过矩形对角线的直线。 标记顶点。
    6. 画出双曲线的两个分支。

    识别中心时要小心。 标准方程\(y−k\)的中心为\(x−h\)和\((h,k)\)。

    示例\(\PageIndex{4}\)

    图表\(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{4}=1\)。

    解决方案：

      。
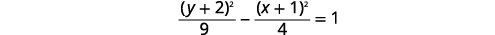    由于\(y^{2}\)-term 为正，因此双曲线向上和向下打开。 。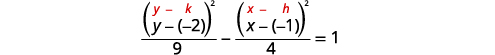
    找到中心，\((h,k)\)。 中心：\((-1,-2)\)
    查找\(a,b\)。 \(a=3 b=2\)
    绘制一个矩形，该矩形穿过中心上方和下方的点\(3\)
    \(2\)单位以及中心左侧/右侧的单位。
    绘制渐近线，即穿过矩形对角线的直线。
    标记顶点。
    绘制树枝的图表。    		 。
    表 11.4.6
    练习\(\PageIndex{7}\)

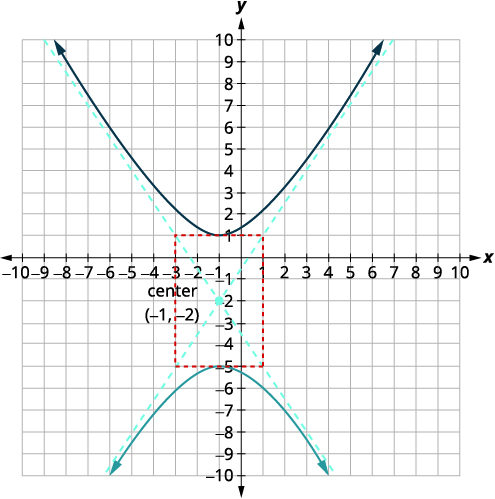    图表\(\frac{(y+3)^{2}}{16}-\frac{(x+2)^{2}}{9}=1\)。

    回答
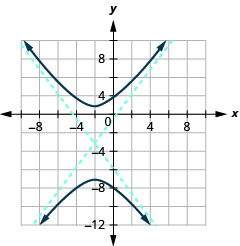
    该图显示了 x 轴和 y 轴，它们均沿负方向和正方向延伸，但间隔未标记，中心位于（负 2，负 3），渐近线穿过（负 5，负 7）和（1，1），渐近线穿过（负 5、1）和（1、7），以及分支它穿过顶点（负 2，1）和（负 2，负 7），然后向上和向下打开。
    图 11.4.22
    练习\(\PageIndex{8}\)

    图表\(\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{9}=1\)。

    回答
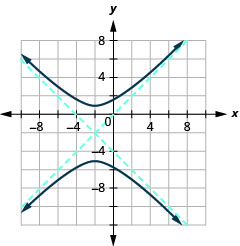
    该图显示了 x 轴和 y 轴，它们均沿负方向和正方向延伸，但间隔未标记，中心位于（负 2，负 2），渐近线穿过（负 5，负 5）和（1，负 5），渐近线穿过（负 5，1）和（1，负 5），以及穿过顶点（负 2、1）和（负 2、负 5）并上下打开的分支。
    图 11.4.23

    同样，有时候我们必须将方程式转换为标准形式作为第一步。

    示例\(\PageIndex{5}\)

    用标准形式和图表写下方程\(4 x^{2}-9 y^{2}-24 x-36 y-36=0\)。

    解决方案：

      。
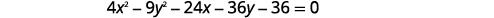    要获得标准形态，请完成方块。 。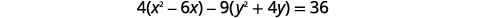
      。
      。
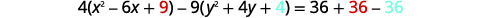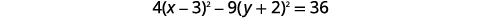    将每个项除\(36\)以得出常数\(1\)。 。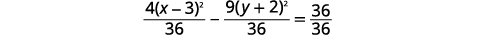
      。
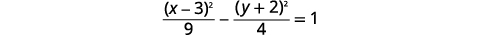    由于\(x^{2}\)-term 为正，因此双曲线左右打开。  
    找到中心，\((h,k)\)。 中心：\((3, -2)\)
    查找\(a,b\)。

    \(a=3\)

    \(b=4\)
    绘制一个矩形，该矩形穿过中心左侧/右侧的点\(3\)\(2\)单位以及中心上方和下方的单位。
    绘制渐近线，即穿过矩形对角线的直线。
    标记顶点。
    绘制树枝的图表。    		 。
    表 11.4.7
    练习\(\PageIndex{9}\)
    1. 用标准形式写下方程式然后
    2. 图表\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)。
    回答
    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-2)^{2}}{9}=1\)
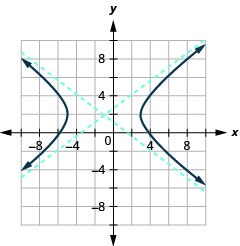
    该图显示了沿负向和正方向延伸但间隔未标记的 x 轴和 y 轴，其中心为负 1、2、穿过（负 5、5）和（3，负 1）的渐近线和穿过（3、5）和（负 5，负 1）的渐近线，以及分支穿过顶点（负 5、2）和（3、2），然后左右打开。
    图 11.4.31
    练习\(\PageIndex{10}\)
    1. 用标准形式写下方程式然后
    2. 图表\(16 x^{2}-25 y^{2}+96 x-50 y-281=0\)。
    回答
    1. \(\frac{(x+3)^{2}}{25}-\frac{(y+1)^{2}}{16}=1\)
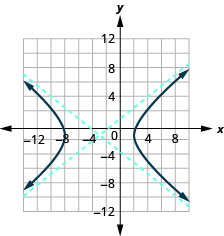
    该图显示了 x 轴和 y 轴，它们均沿负方向和正方向延伸，但间隔未标记，中心为负 3，负 1）、穿过（负 8、负 5）和（2、3）的渐近线以及穿过（负 8、3）和（2，负 5）的渐近线，以及穿过顶点（负 8，负 1）和（2，负 1）并左右打开的分支。
    图 11.4.32

    通过圆锥截面的方程识别圆锥截面

    现在我们已经完成了对圆锥截面的研究，我们将研究不同的方程并找出一些通过其方程来识别圆锥的方法。 当我们得到一个方程来绘制图形时，识别圆锥会很有帮助，这样我们就知道接下来要采取什么步骤。

    要从其方程中识别圆锥曲线，将变量项放在方程的一侧，将常量放在另一侧会更容易。

    圆锥的 \(x^{2}\)-和\(y^{2}\)-术语的特征 示例
    抛物线 \ (x^ {2}\)-和\(y^{2}\)-terms” >要\(x^{2}\)么是 OR\(y^{2}\)。 只有一个变量是平方的。 \(x=3 y^{2}-2 y+1\)
    圈子 \ (x^ {2}\)-和\(y^{2}\)-terms” >\(x^{2}\)\(y^{2}\)-和-项的系数相同。 \(x^{2}+y^{2}=49\)
    椭圆 \ (x^ {2}\)-和\(y^{2}\)-terms” >\(x^{2}\)\(y^{2}\)-和-项具有相同的符号，不同的系数。 \(4 x^{2}+25 y^{2}=100\)
    双曲线 \ (x^ {2}\)-和\(y^{2}\)-terms” >\(x^{2}\)\(y^{2}\)-和-项有不同的符号，不同的系数。 \(25 y^{2}-4 x^{2}=100\)
    表 11.4.8
    示例\(\PageIndex{6}\)

    将每个方程的图形标识为圆形、抛物线、椭圆或双曲线。

    1. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    2. \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
    3. \(x^{2}+y^{2}-6 x-8 y=0\)
    4. \(y=-2 x^{2}-4 x-5\)

    解决方案：

    a.\(x^{2}\)-和\(y^{2}\)-项具有相同的符号和不同的系数。

    \(9 x^{2}+4 y^{2}+56 y+160=0\)

    椭圆

    b.\(x^{2}\)-和\(y^{2}\)-项有不同的符号和不同的系数。

    \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)

    双曲线

    c.\(x^{2}\)-和\(y^{2}\)-项的系数相同。

    \(x^{2}+y^{2}-6 x-8 y=0\)

    圈

    d. 只有一个变量是平方的。\(x\)

    \(y=-2 x^{2}-4 x-5\)

    抛物线

    练习\(\PageIndex{11}\)

    将每个方程的图形标识为圆形、抛物线、椭圆或双曲线。

    1. \(x^{2}+y^{2}-8 x-6 y=0\)
    2. \(4 x^{2}+25 y^{2}=100\)
    3. \(y=6 x^{2}+2 x-1\)
    4. \(16 y^{2}-9 x^{2}=144\)
    回答
    1. 圈
    2. 椭圆
    3. 抛物线
    4. 双曲线
    练习\(\PageIndex{12}\)

    将每个方程的图形标识为圆形、抛物线、椭圆或双曲线。

    1. \(16 x^{2}+9 y^{2}=144\)
    2. \(y=2 x^{2}+4 x+6\)
    3. \(x^{2}+y^{2}+2 x+6 y+9=0\)
    4. \(4 x^{2}-16 y^{2}=64\)
    回答
    1. 椭圆
    2. 抛物线
    3. 圈
    4. 双曲线

    访问这些在线资源以获取更多说明和使用双曲线练习。

    • 绘制以原点为中心的双曲线图
    • 绘制中心不在原点的双曲线图
    • 以一般形式绘制双曲线图
    • 以一般形式识别圆锥截面

    关键概念

    • 双曲线：双曲线是平面中的所有点，其与两个固定点的距离之差恒定。
    该图显示了一个双打磨的右圆锥体，该圆锥被平行于圆锥体垂直轴的平面切成双曲线。 这个数字被标记为 “双曲线”。
    图 11.4.1
    • 每个定点都称为双曲线的焦点。
      穿过焦点的直线称为横轴。
      横轴与双曲线相交的两个点均为双曲线的顶点。
      连接焦点的线段的中点称为双曲线的中心。
      垂直于穿过中心的横轴的直线称为共轭轴。
      图表的每一部分都被称为双曲线的一个分支。
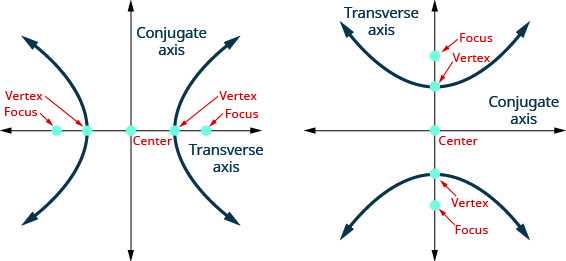
      该图显示了两张双曲线图。 第一张图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 顶点和焦点以位于横轴（即 x 轴）上的点显示。 树枝穿过顶点并左右打开。 y 轴是共轭轴。 第二张图显示了 x 轴和 y 轴，它们均沿负向和正方向运行，但间隔未标记。 双曲线的中心是原点。 顶点和焦点线以位于横轴（即 y 轴）上的点来显示。 树枝穿过顶点并上下开放。 x 轴是共轭轴。

    图 11.4.2

    方程的标准形式是带中心的双曲线\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    方向 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\(x\)-axis 上的横轴。
    左右打开    		 \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\(y\)-axis 上的横轴。
    向上和向下打开
    顶点 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\((0,-a),(0, a)\)
    \(x\)-拦截 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >无
    \(y\)-拦截 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >无 \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\((0,-a),(0, a)\)
    矩形 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >使用\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >使用\((0, \pm a)( \pm b, 0)\)
    渐近线 \ (\ frac {x^ {2}} {a^ {2}}-\ frac {y^ {2}} {b^ {2}} =1\)” >\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}}-\ frac {x^ {2}} {b^ {2}} =1\)” >\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    表 11.4.1
    • 如何绘制以为中心的双曲线\((0,0)\)。
      1. 用标准形式写出方程式。
      2. 确定横轴是水平还是垂直。
      3. 找到顶点。
      4. 绘制以原点为中心的矩形，其中一个轴\(±a\)与另一个轴相交\(±b\)。
      5. 绘制渐近线——穿过矩形对角线的直线。
      6. 画出双曲线的两个分支。

    方程的标准形式是带中心的双曲线\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    方向 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\) “>横轴是水平的。 左右打开 \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\) “>横轴是垂直的。 向上和向下打开
    中心 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\)” >\((h,k)\) \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\)” >\((h,k)\)
    顶点 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\)” > 中心左侧和右侧的\(a\)单位 \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\)” > 中心上方和下方的\(a\)单位
    矩形 \ (\ frac {(x-h) ^ {2}} {a^ {2}}-\ frac {(y-k) ^ {2}} {b^ {2}} =1\) “>在中心上方/下方使用中心\(a\)\(b\)单位左/右的单位 \ (\ frac {(y-k) ^ {2}} {a^ {2}}-\ frac {(x-h) ^ {2}} {b^ {2}} =1\)” >使用中心\(a\)单位上方/下方中心左侧/右侧的\(b\)单位
    表 11.4.4
    • 如何绘制以为中心的双曲线\((h,k)\)。
      1. 用标准形式写出方程式。
      2. 确定横轴是水平还是垂直。
      3. 找到中心然后\(a,b\).
      4. 绘制以\((h,k)\)使用为中心的矩形\(a,b\)。
      5. 绘制渐近线——穿过矩形对角线的直线。 标记顶点。
      6. 画出双曲线的两个分支。
    圆锥的 \(x^{2}\)-和\(y^{2}\)-术语的特征 示例
    抛物线 \ (x^ {2}\)-和\(y^{2}\)-terms” >要\(x^{2}\)么是 OR\(y^{2}\)。 只有一个变量是平方的。 \(x=3 y^{2}-2 y+1\)
    圈子 \ (x^ {2}\)-和\(y^{2}\)-terms” >\(x^{2}\)\(y^{2}\)-和-项的系数相同。 \(x^{2}+y^{2}=49\)
    椭圆 \ (x^ {2}\)-和\(y^{2}\)-terms” >\(x^{2}\)\(y^{2}\)-和-项具有相同的符号，不同的系数。 \(4 x^{2}+25 y^{2}=100\)
    双曲线 \ (x^ {2}\)-和\(y^{2}\)-terms” >\(x^{2}\)\(y^{2}\)-和-项有不同的符号，不同的系数。 \(25 y^{2}-4 x^{2}=100\)
    表 11.4.8

    词汇表

    双曲线
    双曲线被定义为平面中的所有点，这些点与两个固定点的距离之差不变。