第 10 章复习练习
- Page ID
- 204021
章节复习练习
查找复合函数和逆函数
在以下练习中,针对每对函数,找到
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
1。 \(f(x)=7 x-2\)和\(g(x)=5 x+1\)
2。 \(f(x)=4 x\)和\(g(x)=x^{2}+3 x\)
- 回答
-
2。
- \(4 x^{2}+12 x\)
- \(16 x^{2}+12 x\)
- \(4 x^{3}+12 x^{2}\)
在以下练习中,评估构图。
- 对于函数\(f(x)=3 x^{2}+2\)和\(g(x)=4 x-3\),请查找
- \((f \circ g)(-3)\)
- \((g \circ f)(-2)\)
- \((f \circ f)(-1)\)
- 对于函数\(f(x)=2 x^{3}+5\)和\(g(x)=3 x^{2}-7\),请查找
- \((f \circ g)(-1)\)
- \((g \circ f)(-2)\)
- \((g \circ g)(1)\)
- 回答
-
2。
- \(-123\)
- \(356\)
- \(41\)
在以下练习中,对于每组有序对,确定它是否代表一个函数,如果是,则是一对一的函数。
- \(\begin{array}{l}{\{(-3,-5),(-2,-4),(-1,-3),(0,-2)} , {(-1,-1),(-2,0),(-3,1) \}}\end{array}\)
- \(\begin{array}{l}{\{(-3,0),(-2,-2),(-1,0),(0,1)} , {(1,2),(2,1),(3,-1) \}}\end{array}\)
- \(\begin{array}{l}{\{(-3,3),(-2,1),(-1,-1),(0,-3)} , {(1,-5),(2,-4),(3,-2) \}}\end{array}\)
- 回答
-
2。 功能;不是一对一
在以下练习中,确定每个图形是否是函数的图形,如果是,是否是一对一的。
-
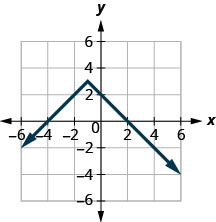
图 10.E.1
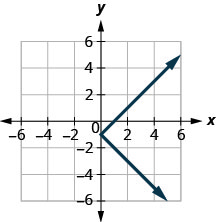
图 10.E.2
-
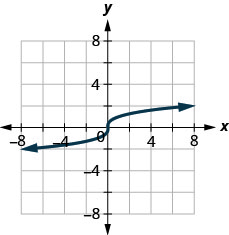
图 10.E.3
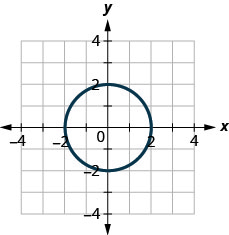
图 10.E.4
- 回答
-
1。
- 功能;不是一对一
- 不是函数
在以下练习中,找到该函数的逆函数。 确定逆函数的域和范围。
- \(\{(-3,10),(-2,5),(-1,2),(0,1)\}\)
- 回答
-
1。 反向函数:\(\{(10,-3),(5,-2),(2,-1),(1,0)\}\). 域:\(\{1,2,5,10\}\)。 范围:\(\{-3,-2,-1,0\}\)。
在以下练习中,绘制所示一对一函数的逆函数。
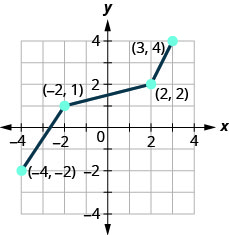
- 回答
-
自行解决
在以下练习中,验证函数是否为反函数。
- \(\begin{array}{l}{f(x)=3 x+7 \text { and }} {g(x)=\frac{x-7}{3}}\end{array}\)
- \(\begin{array}{l}{f(x)=2 x+9 \text { and }} {g(x)=\frac{x+9}{2}}\end{array}\)
- 回答
-
1。 \(g(f(x))=x,\)\(f(g(x))=x,\)所以它们是反向的。
- \(f(x)=6 x-11\)
- \(f(x)=x^{3}+13\)
- \(f(x)=\frac{1}{x+5}\)
- \(f(x)=\sqrt[5]{x-1}\)
- 回答
-
1。 \(f^{-1}(x)=\frac{x+11}{6}\)
3。 \(f^{-1}(x)=\frac{1}{x}-5\)
计算指数函数并绘制其图形
在以下练习中,绘制以下每个函数的图表。
- \(f(x)=4^{x}\)
- \(f(x)=\left(\frac{1}{5}\right)^{x}\)
- \(g(x)=(0.75)^{x}\)
- \(g(x)=3^{x+2}\)
- \(f(x)=(2.3)^{x}-3\)
- \(f(x)=e^{x}+5\)
- \(f(x)=-e^{x}\)
- 回答
-
1。
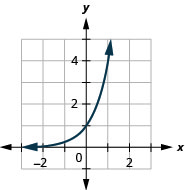
图 10.E.6 3。
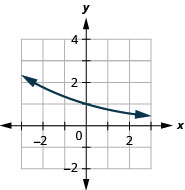
图 10.E.7 5。
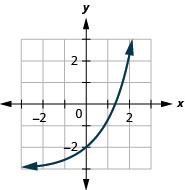
图 10.E.8 7。
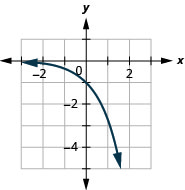
图 10.E.9
在以下练习中,求解每个方程。
- \(3^{5 x-6}=81\)
- \(2^{x^{2}}=16\)
- \(9^{x}=27\)
- \(5^{x^{2}+2 x}=\frac{1}{5}\)
- \(e^{4 x} \cdot e^{7}=e^{19}\)
- \(\frac{e^{x^{2}}}{e^{15}}=e^{2 x}\)
- 回答
-
2。 \(x=-2, x=2\)
4。 \(x=-1\)
6。 \(x=-3, x=5\)
在以下练习中,求解。
- 费利克斯在储蓄账户\(12,000\)中投资了美元。 如果利率为\(4\) %,则每种复利方法在\(12\)年内账户中会有多少?
- 化合物季刊
- 化合物月报
- 持续化合物
- 赛义德将美元存\(20,000\)入投资账户。 如果投资的年收益率为\(7\)百分比并且持续复利,那么\(30\)多年来他的投资价值将是多少?
- 疾病控制与预防中心的一位研究人员正在研究细菌的生长。 她开始\(150\)对以每小时\(15\)百分比的速度生长的细菌进行实验。 她将每隔一\(24\)小时检查一次细菌。 他会在\(24\)几个小时内发现多少细菌?
- 在过去的五年中,美国的人口以每年\(0.7\)百分比的速度增长到大约\(318,900,000\)。 如果这个比率持续下去,那么未来几年的人口会是\(5\)多少?
- 回答
-
2。 \(\$ 163,323.40\)
4。 \(330,259,000\)
计算对数函数并绘制图表
在以下练习中,从指数形式转换为对数形式。
- \(5^{4}=625\)
- \(10^{-3}=\frac{1}{1,000}\)
- \(63^{\frac{1}{5}}=\sqrt[5]{63}\)
- \(e^{y}=16\)
- 回答
-
2。 \(\log \frac{1}{1,000}=-3\)
4。 \(\ln 16=y\)
在以下练习中,将每个对数方程转换为指数形式。
- \(7=\log _{2} 128\)
- \(5=\log 100,000\)
- \(4=\ln x\)
- 回答
-
2。 \(100000=10^{5}\)
在以下练习中,求解\(x\)。
- \(\log _{x} 125=3\)
- \(\log _{7} x=-2\)
- \(\log _{\frac{1}{2}} \frac{1}{16}=x\)
- 回答
-
1。 \(x=5\)
3。 \(x=4\)
在以下练习中,无需使用计算器即可找到每个对数的确切值。
- \(\log _{2} 32\)
- \(\log _{8} 1\)
- \(\log _{3} \frac{1}{9}\)
- 回答
-
2。 \(0\)
在以下练习中,绘制每个对数函数的图表。
- \(y=\log _{5} x\)
- \(y=\log _{\frac{1}{4}} x\)
- \(y=\log _{0.8} x\)
- 回答
-
1。
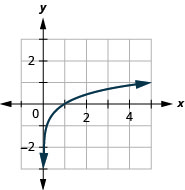
图 10.E.10 3。
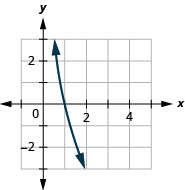
图 10.E.11
在以下练习中,求解每个对数方程。
- \(\log _{a} 36=5\)
- \(\ln x=-3\)
- \(\log _{2}(5 x-7)=3\)
- \(\ln e^{3 x}=24\)
- \(\log \left(x^{2}-21\right)=2\)
- 回答
-
2。 \(x=e^{-3}\)
4。 \(x=8\)
强度为每平方英寸\(10^{−3}\)瓦特的火车哨的分贝等级是多少?
- 回答
-
\(90\)dB
使用对数的属性
在以下练习中,使用对数的属性进行计算。
-
- \(\log _{7} 1\)
- \(\log _{12} 12\)
-
- \(5^{\log _{5} 13}\)
- \(\log _{3} 3^{-9}\)
-
- \(10^{\log \sqrt{5}}\)
- \(\log 10^{-3}\)
-
- \(e^{\ln 8}\)
- \(\ln e^{5}\)
- 回答
-
2。
- \(13\)
- \(-9\)
4。
- \(8\)
- \(5\)
在以下练习中,使用对数乘积属性将每个对数写成对数之和。 尽可能简化。
- \(\log _{4}(64 x y)\)
- \(\log 10,000 m\)
- 回答
-
2。 \(4+\log m\)
在以下练习中,使用对数的商属性将每个对数写成对数之和。 尽可能简化。
- \(\log _{7} \frac{49}{y}\)
- \(\ln \frac{e^{5}}{2}\)
- 回答
-
2。 \(5-\ln 2\)
在以下练习中,使用对数的幂属性来扩展每个对数。 尽可能简化。
- \(\log x^{-9}\)
- \(\log _{4} \sqrt[7]{z}\)
- 回答
-
2。 \(\frac{1}{7} \log _{4} z\)
在以下练习中,使用对数的属性将每个对数写成对数之和。 尽可能简化。
- \(\log _{3}\left(\sqrt{4} x^{7} y^{8}\right)\)
- \(\log _{5} \frac{8 a^{2} b^{6} c}{d^{3}}\)
- \(\ln \frac{\sqrt{3 x^{2}-y^{2}}}{z^{4}}\)
- \(\log _{6} \sqrt[3]{\frac{7 x^{2}}{6 y^{3} z^{5}}}\)
- 回答
-
2。 \(\begin{array}{l}{\log _{5} 8+2 \log _{5} a+6 \log _{5} b} {+\log _{5} c-3 \log _{5} d}\end{array}\)
4。 \(\begin{array}{l}{\frac{1}{3}\left(\log _{6} 7+2 \log _{6} x-1-3 \log _{6} y\right.} {-5 \log _{6} z )}\end{array}\)
在以下练习中,使用对数属性来压缩对数。 尽可能简化。
- \(\log _{2} 56-\log _{2} 7\)
- \(3 \log _{3} x+7 \log _{3} y\)
- \(\log _{5}\left(x^{2}-16\right)-2 \log _{5}(x+4)\)
- \(\frac{1}{4} \log y-2 \log (y-3)\)
- 回答
-
2。 \(\log _{3} x^{3} y^{7}\)
4。 \(\log \frac{\sqrt[4]{y}}{(y-3)^{2}}\)
在以下练习中,四舍五入到小数点后三位,近似每个对数。
- \(\log _{5} 97\)
- \(\log _{\sqrt{3}} 16\)
- 回答
-
2。 \(5.047\)
求解指数和对数方程
在以下练习中,求解\(x\)。
- \(3 \log _{5} x=\log _{5} 216\)
- \(\log _{2} x+\log _{2}(x-2)=3\)
- \(\log (x-1)-\log (3 x+5)=-\log x\)
- \(\log _{4}(x-2)+\log _{4}(x+5)=\log _{4} 8\)
- \(\ln (3 x-2)=\ln (x+4)+\ln 2\)
- 回答
-
2。 \(x=4\)
4。 \(x=3\)
在以下练习中,求解每个指数方程。 找到确切的答案,然后将其近似到小数点后三位。
- \(2^{x}=101\)
- \(e^{x}=23\)
- \(\left(\frac{1}{3}\right)^{x}=7\)
- \(7 e^{x+3}=28\)
- \(e^{x-4}+8=23\)
- 回答
-
1。 \(x=\frac{\log 101}{\log 2} \approx 6.658\)
3。 \(x=\frac{\log 7}{\log \frac{1}{3}} \approx-1.771\)
5。 \(x=\ln 15+4 \approx 6.708\)
- 杰罗姆年纪\(18,000\)就投资美元\(17\)。 他希望\(30,000\)当他转身时,这些投资将值美元\(26\)。 如果利息持续增加,他大约需要多少增长率才能实现目标? 这是合理的预期吗?
- Elise 将美元投资\(4500\)于一个账户,该账户每月可复合利息并赚取\(6\)百分比。她的钱需要多长时间才能翻一番?
- 研究人员记录说,某些细菌种群\(300\)在\(8\)数小时内从增长\(100\)到. 以这种增长速度,\(24\)几个小时内会有多少细菌?
- 老鼠数量可以在\(8\)几个月内翻一番\(\left(A=2 A_{0}\right)\)。 老鼠数量需要多长时间才能增加三倍?
- 放射性碘的半衰期是\(60\)几天。 \(40\)几天之内会剩下多少\(50\)毫克样本?
- 回答
-
2。 \(11.6\)年份
4。 \(12.7\)月
练习测试
- 对于函数\(g(x)=8x−3\),\(f(x)=6x+1\)然后找到
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- 确定以下一组有序对是否代表一个函数,如果是,则该函数是一对一的。 \(\{(-2,2),(-1,-3),(0,1),(1,-2),(2,-3)\}\)
- 确定每个图形是否是函数的图形,如果是,是否是一对一的。
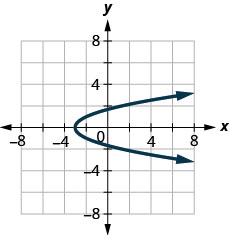
图 10.E.12
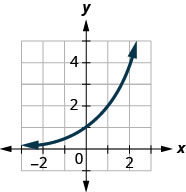
图 10.E.13
- 在同一个坐标系上绘制图表,显示一对一函数的逆函数。
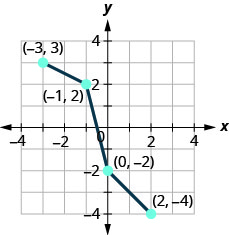
5。 找出函数的逆函数\(f(x)=x^{5}−9\)。
6。 绘制函数图表\(g(x)=2^{x-3}\)。
7。 求解方程\(2^{2 x-4}=64\)。
8。 求解方程\(\frac{e^{x^{2}}}{e^{4}}=e^{3 x}\)。
9。 梅根在储蓄账户\(21,000\)中投资了美元。 如果利率为\(5\) %,那么通过每种复利方法,按\(8\)年计算,账户中将有多少?
- 化合物季刊
- 化合物月报
- 持续化合物
10。 将方程从指数形式转换为对数形式:\(10^{-2}=\frac{1}{100}\).
11。 将方程从对数方程转换为指数形式:\(3=\log _{7} 343\).
12。 求解\(x\):\(\log _{5} x=-3\)
13。 评估日志\(_{11} 1\)。
14。 评估\(\log _{4} \frac{1}{64}\)。
15。 绘制函数图表\(y=\log _{3} x\)。
16。 求解\(x\):\(\log \left(x^{2}-39\right)=1\)
17。 强度为每平方英寸\(10^{−8}\)瓦特的小型风扇的分贝水平是多少?
18。 分别进行评估。
- \(6^{\log _{6} 17}\)
- \(\log _{9} 9^{-3}\)
- 回答
-
1。
- \(48 x-17\)
- \(48 x+5\)
- \(48 x^{2}-10 x-3\)
3。
- 不是函数
- 一对一功能
5。 \(f^{-1}(x)=\sqrt[5]{x+9}\)
7。 \(x=5\)
9。
- $\(31,250.74\)
- $\(31,302.29\)
- $\(31,328.32\)
11。 \(343=7^{3}\)
13。 \(0\)
15。
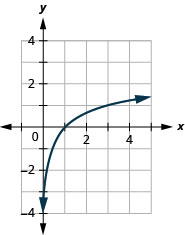
图 10.E.15 17。 \(40\)dB
在以下练习中,使用对数的属性将每个表达式写成对数之和,尽可能进行简化。
- \(\log _{5} 25 a b\)
- \(\ln \frac{e^{12}}{8}\)
- \(\log _{2} \sqrt[4]{\frac{5 x^{3}}{16 y^{2} z^{7}}}\)
- 回答
-
1。 \(2+\log _{5} a+\log _{5} b\)
3。 \(\begin{array}{l}{\frac{1}{4}\left(\log _{2} 5+3 \log _{2} x-4-2 \log _{2} y\right.} {-7 \log _{2} z )}\end{array}\)
在以下练习中,使用对数属性来压缩对数,尽可能进行简化。
- \(5 \log _{4} x+3 \log _{4} y\)
- \(\frac{1}{6} \log x-3 \log (x+5)\)
- 四舍五入到小数点后三位,近似值\(\log _{4} 73\)。
- 求解\(x\):\(\log _{7}(x+2)+\log _{7}(x-3)=\log _{7} 24\)
- 回答
-
2。 \(\log \frac{\sqrt[6]{x}}{(x+5)^{3}}\)
4。 \(x=6\)
在以下练习中,求解每个指数方程。 找到确切的答案,然后将其近似到小数点后三位。
- \(\left(\frac{1}{5}\right)^{x}=9\)
- \(5 e^{x-4}=40\)
- 雅各布将美元投资\(14,000\)于一个账户,该账户每季度复合利息并赚取\(4\)百分比。 他的钱要多久才能翻一番?
- 研究人员记录说,某些细菌种群\(700\)在\(5\)数小时内从增长\(500\)到. 以这种增长速度,\(20\)几个小时内会有多少细菌?
- 某些甲虫种群可以在\(3\)几个月内翻一番\(\left(A=2 A_{0}\right)\)。 甲虫种群需要多长时间才能增加三倍?
- 回答
-
2。 \(x=\ln 8+4 \approx 6.079\)
4。 \(1,921\)细菌


