Skip to main content
Global

10.2E：练习

  1. Last updated
  2. Save as PDF
  • Page ID
    204010

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    练习成就完美

    练习\(\PageIndex{19}\) Find and Evaluate Composite Functions

    在以下练习中，找到

    1. \((f \circ g)(x)\)
    2. \((g \circ f)(x)\)
    3. \((f \cdot g)(x)\)
    1. \(f(x)=4 x+3\)和\(g(x)=2 x+5\)
    2. \(f(x)=3 x-1\)和\(g(x)=5 x-3\)
    3. \(f(x)=6 x-5\)和\(g(x)=4 x+1\)
    4. \(f(x)=2 x+7\)和\(g(x)=3 x-4\)
    5. \(f(x)=3 x\)和\(g(x)=2 x^{2}-3 x\)
    6. \(f(x)=2 x\)和\(g(x)=3 x^{2}-1\)
    7. \(f(x)=2 x-1\)和\(g(x)=x^{2}+2\)
    8. \(f(x)=4 x+3\)和\(g(x)=x^{2}-4\)
    回答

    1。

    1. \(8x+23\)
    2. \(8x+11\)
    3. \(8 x^{2}+26 x+15\)

    3。

    1. \(24x+1\)
    2. \(24x-19\)
    3. \(24x^{2}+19x-5\)

    5。

    1. \(6 x^{2}-9 x\)
    2. \(18 x^{2}-9 x\)
    3. \(6 x^{3}-9 x^{2}\)

    7。

    1. \(2 x^{2}+3\)
    2. \(4 x^{2}-4 x+3\)
    3. \(2 x^{3}-x^{2}+4 x-2\)
    练习\(\PageIndex{20}\) Find and Evaluate Composite Functions

    在以下练习中，找到描述的值。

    1. 对于函数\(f(x)=2 x^{2}+3\)和\(g(x)=5x-1\)，请查找
      1. \((f \circ g)(-2)\)
      2. \((g \circ f)(-3)\)
      3. \((f \circ f)(-1)\)
    2. 对于函数\(f(x)=5 x^{2}-1\)和\(g(x)=4x−1\)，请查找
      1. \((f \circ g)(1)\)
      2. \((g \circ f)(-1)\)
      3. \((f \circ f)(2)\)
    3. 对于函数\(f(x)=2x^{3}\)和\(g(x)=3x^{2}+2\)，请查找
      1. \((f \circ g)(-1)\)
      2. \((g \circ f)(1)\)
      3. \((g \circ g)(1)\)
    4. 对于函数\(f(x)=3 x^{3}+1\)和\(g(x)=2 x^{2}=3\)，请查找
      1. \((f \circ g)(-2)\)
      2. \((g \circ f)(-1)\)
      3. \((g \circ g)(1)\)
    回答

    1。

    1. \(245\)
    2. \(104\)
    3. \(53\)

    3。

    1. \(250\)
    2. \(14\)
    3. \(77\)
    练习\(\PageIndex{21}\) Determine Whether a Function is One-to-One

    在以下练习中，确定这组有序对是否代表一个函数，如果是，则是函数一对一。

    1. \(\begin{array}{l}{\{(-3,9),(-2,4),(-1,1),(0,0)}, {(1,1),(2,4),(3,9) \}}\end{array}\)
    2. \(\begin{array}{l}{\{(9,-3),(4,-2),(1,-1),(0,0)}, {(1,1),(4,2),(9,3) \}}\end{array}\)
    3. \(\begin{array}{l}{\{(-3,-5),(-2,-3),(-1,-1)}, {(0,1),(1,3),(2,5),(3,7) \}}\end{array}\)
    4. \(\begin{array}{l}{\{(5,3),(4,2),(3,1),(2,0)}, {(1,-1),(0,-2),(-1,-3) \}}\end{array}\)
    回答

    1。 功能；不是一对一

    3。 一对一功能

    练习\(\PageIndex{22}\) Determine Whether a Function is One-to-One

    在以下练习中，确定每个图形是否是函数的图形，如果是，是否是一对一的。

    1。


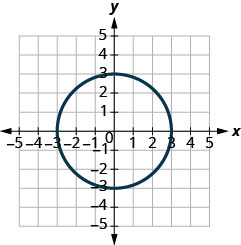
    1. 此图显示了一个圆的图形，圆心位于原点，半径为 3。
      图 10.1.65

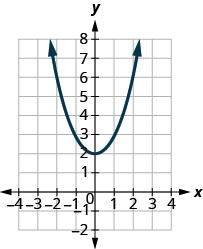
    2. 此图显示了抛物线向上开口且顶点位于 (0k, 2) 的图形。
      图 10.1.66

    2。


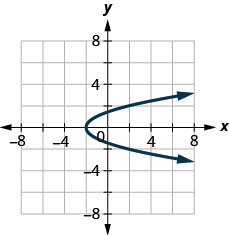
    1. 此图显示了右侧的抛物线开口，顶点位于（负 2, 0）。
      图 10.1.67

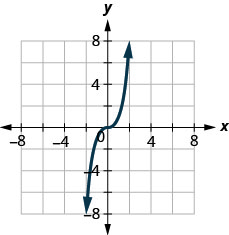
    2. 此图显示了具有奇数阶的多项式的图形，因此它从第三象限开始，增加到原点，然后通过第一个象限继续增加。
      图 10.1.68

    3。


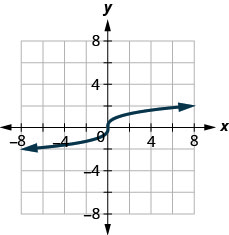
    1. 此图显示了一条曲线的图形，该曲线从（负 6 负 2）开始增加到原点，然后继续缓慢增加到 (6, 2)。
      图 10.1.69

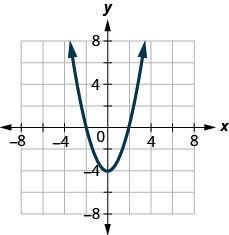
    2. 此图显示了一个向上开口的抛物线，顶点位于 (0，负 4)。
      图 10.1.70

    4。


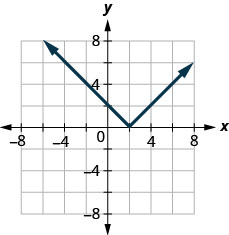
    1. 此图显示一条直线段从 (负 4, 6) 减至 (2, 0)，之后它从 (2, 0) 增加到 (6, 4)。
      图 10.1.71

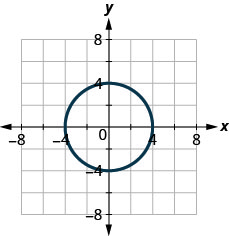
    2. 此图显示了一个半径为 4 且中心位于原点的圆。
      图 10.1.72
    回答

    1。

    1. 不是函数
    2. 功能；不是一对一

    3。

    1. 一对一功能
    2. 功能；不是一对一
    练习\(\PageIndex{23}\) Determine Whether a Function is One-to-One

    在以下练习中，找到每个函数的逆函数。 确定逆函数的域和范围。

    1. \(\{(2,1),(4,2),(6,3),(8,4)\}\)
    2. \(\{(6,2),(9,5),(12,8),(15,11)\}\)
    3. \(\{(0,-2),(1,3),(2,7),(3,12)\}\)
    4. \(\{(0,0),(1,1),(2,4),(3,9)\}\)
    5. \(\{(-2,-3),(-1,-1),(0,1),(1,3)\}\)
    6. \(\{(5,3),(4,2),(3,1),(2,0)\}\)
    回答

    1。 \(\begin{array}{l}{\text { Inverse function: }\{(1,2),(2,4),(3,6),(4,8)\} . \text { Domain: }\{1,2,3,4\} . \text { Range: }} {\{2,4,6,8\} .}\end{array}\)

    3。 \(\begin{array}{l}{\text { Inverse function: }\{(-2,0),(3,1),(7,2),(12,3)\} . \text { Domain: }\{-2,3,7,12\} \text { . }} {\text { Range: }\{0,1,2,3\}}\end{array}\)

    5。 \(\begin{array}{l}{\text { Inverse function: }\{(-3,-2),(-1,-1),(1,0),(3,1)\} . \text { Domain: }} {\{-3,-1,1,3\} . \text { Range: }\{-2,-1,0,1\}}\end{array}\)

    练习\(\PageIndex{24}\) Determine Whether a Function is One-to-One

    在以下练习中，在同一个坐标系上绘制一对一函数的逆函数。


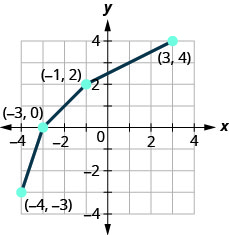
    1. 此图显示了从（负 4、负 3）到（负 3、0）、再到（负 1、2）再到（负 1、4）的一系列线段。
      图 10.1.73

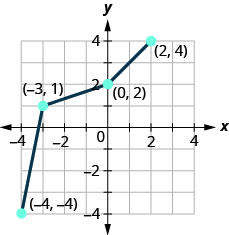
    2. 此图显示了从（负 4、负 4）到（负 3、1）、再到（0、2）再到（2、4）的一系列线段。
      图 10.1.74

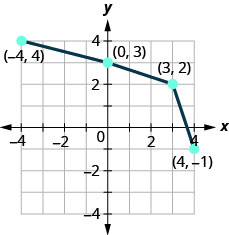
    3. 此图显示了从（负 4、4）到（0、3）、再到（3、2）再到（4、负 1）的一系列线段。
      图 10.1.75

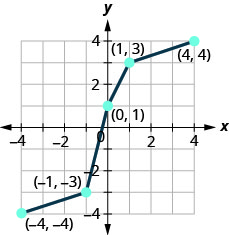
    4. 此图显示了一系列线段，从（负 4，负 4）到（负 1，负 3），然后到（0，1），再到（1，3），再到（4，4）。
      图 10.1.76
    回答

    1。

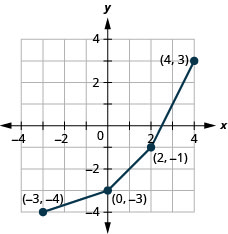
    此图显示了从（负 3，负 4）到（0，负 3），再到（2，负 1），再到（4、3）的一系列线段。
    图 10.1.77

    3。

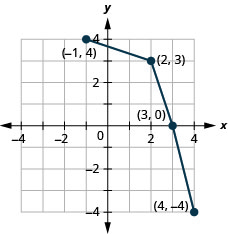
    此图显示了从（负 1、4）到（2、3）、再到（3、0）、再到（4、负 4）的一系列线段。
    图 10.1.78
    练习\(\PageIndex{25}\) Determine Whether the given functions are inverses

    在以下练习中，确定给定函数是否为反函数。

    1. \(f(x)=x+8\)和\(g(x)=x-8\)
    2. \(f(x)=x-9\)和\(g(x)=x+9\)
    3. \(f(x)=7 x\)和\(g(x)=\frac{x}{7}\)
    4. \(f(x)=\frac{x}{11}\)和\(g(x)=11 x\)
    5. \(f(x)=7 x+3\)和\(g(x)=\frac{x-3}{7}\)
    6. \(f(x)=5 x-4\)和\(g(x)=\frac{x-4}{5}\)
    7. \(f(x)=\sqrt{x+2}\)和\(g(x)=x^{2}-2\)
    8. \(f(x)=\sqrt[3]{x-4}\)和\(g(x)=x^{3}+4\)
    回答

    1。 \(g(f(x))=x,\)\(f(g(x))=x,\)所以它们是反向的。

    3。 \(g(f(x))=x,\)\(f(g(x))=x,\)所以它们是反向的。

    5。 \(g(f(x))=x,\)\(f(g(x))=x,\)所以它们是反向的。

    7。 \(g(f(x))=x,\)\(f(g(x))=x,\)所以它们是反向的（对于非负数）\(x )\)

    练习\(\PageIndex{26}\) Determine the inverse of a function

    在以下练习中，找到每个函数的逆函数。

    1. \(f(x)=x-12\)
    2. \(f(x)=x+17\)
    3. \(f(x)=9 x\)
    4. \(f(x)=8 x\)
    5. \(f(x)=\frac{x}{6}\)
    6. \(f(x)=\frac{x}{4}\)
    7. \(f(x)=6 x-7\)
    8. \(f(x)=7 x-1\)
    9. \(f(x)=-2 x+5\)
    10. \(f(x)=-5 x-4\)
    11. \(f(x)=x^{2}+6, x \geq 0\)
    12. \(f(x)=x^{2}-9, x \geq 0\)
    13. \(f(x)=x^{3}-4\)
    14. \(f(x)=x^{3}+6\)
    15. \(f(x)=\frac{1}{x+2}\)
    16. \(f(x)=\frac{1}{x-6}\)
    17. \(f(x)=\sqrt{x-2}, x \geq 2\)
    18. \(f(x)=\sqrt{x+8}, x \geq-8\)
    19. \(f(x)=\sqrt[3]{x-3}\)
    20. \(f(x)=\sqrt[3]{x+5}\)
    21. \(f(x)=\sqrt[4]{9 x-5}, x \geq \frac{5}{9}\)
    22. \(f(x)=\sqrt[4]{8 x-3}, x \geq \frac{3}{8}\)
    23. \(f(x)=\sqrt[5]{-3 x+5}\)
    24. \(f(x)=\sqrt[5]{-4 x-3}\)
    回答

    1。 \(f^{-1}(x)=x+12\)

    3。 \(f^{-1}(x)=\frac{x}{9}\)

    5。 \(f^{-1}(x)=6 x\)

    7。 \(f^{-1}(x)=\frac{x+7}{6}\)

    9。 \(f^{-1}(x)=\frac{x-5}{-2}\)

    11。 \(f^{-1}(x)=\sqrt{x-6}\)

    13。 \(f^{-1}(x)=\sqrt[3]{x+4}\)

    15。 \(f^{-1}(x)=\frac{1}{x}-2\)

    17。 \(f^{-1}(x)=x^{2}+2, x \geq 0\)

    19。 \(f^{-1}(x)=x^{3}+3\)

    21。 \(f^{-1}(x)=\frac{x^{4}+5}{9}, x \geq 0\)

    23。 \(f^{-1}(x)=\frac{x^{5}-5}{-3}\)

    练习\(\PageIndex{27}\) Writing Exercises
    1. 解释函数的逆图与函数的图形有何关系。
    2. 解释如何从其方程中找到函数的逆函数。 使用示例来演示这些步骤。
    回答

    1。 答案会有所不同。

    自检

    a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

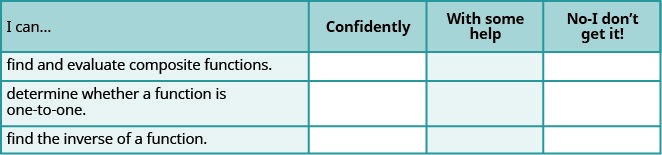
    此表有四行四列。 第一行作为标题，上面写着 “我能”，“自信地，在一些帮助下，不行” 我不明白。™ 标题行下面的第一列显示查找和求值复合函数，确定函数是否为一对一函数，然后求函数的逆函数。 其余单元格为空。
    图 10.1.79

    b. 如果您的大部分支票是：

    ... 自信地。 恭喜！ 您已经实现了本节中的目标。 反思一下你使用的学习技能，这样你就可以继续使用它们。 为了确信自己有能力做这些事情，你做了什么？ 具体一点。

    ... 在一些帮助下。 必须迅速解决这个问题，因为你不掌握的话题会成为你通往成功之路的坑洼。 在数学中，每个主题都建立在以前的工作基础上。 在继续前进之前，请务必确保自己有坚实的基础。 你能向谁寻求帮助？ 你的同学和老师都是很好的资源。 校园里有没有可以提供数学导师的地方？ 你的学习技能可以提高吗？

    ... 不——我不明白！ 这是一个警告信号，你一定不能忽视它。 你应该立即得到帮助，否则你很快就会不知所措。 尽快与您的教师见面，讨论您的情况。 你可以一起制定一个计划，为你提供所需的帮助。