10.3:计算指数函数并绘制其图形
- Page ID
- 204032
在本节结束时,您将能够:
- 图形指数函数
- 求解指数方程
- 在应用程序中使用指数模型
在开始之前,请参加这个准备测验。
- 简化:\(\left(\frac{x^{3}}{x^{2}}\right)\)。
如果您错过了此问题,请查看示例 5.13。 - 评估:a.\(2^{0}\) b\(\left(\frac{1}{3}\right)^{0}\).
如果您错过了此问题,请查看示例 5.14。 - 评估:a.\(2^{−1}\) b\(\left(\frac{1}{3}\right)^{-1}\).
如果您错过了此问题,请查看示例 5.15。
图形指数函数
到目前为止,我们研究的函数并不能为许多自然发生的现象提供模型。 从人口的增长和病毒的传播到放射性衰变和复合兴趣,这些模型与我们迄今为止研究的模型截然不同。 这些模型涉及指数函数。
指数函数是 w here and 形式的\(f(x)=a^{x}\)函数\(a≠1\)。\(a>0\)
指数函数,其中\(a>0\) and 是以下形式的函数\(a≠1\)
\(f(x)=a^{x}\)
请注意,在此函数中,变量是指数。 到目前为止,在我们的函数中,变量是基础。

我们的定义是\(a≠1\)。 如果我们放手\(a=1\),那\(f(x)=a^{x}\)就变成\(f(x)=1^{x}\)。 因为\(1^{x}=1\)对于所有实数,\(f(x)=1\). 这是常量函数。
我们的定义也说\(a>0\)。 比如说,如果我们让一个基数为负数\(−4\),那么什么时候就\(f(x)=(−4)^{x}\)不是一个实数\(x=\frac{1}{2}\)。
\(\begin{aligned} f(x) &=(-4)^{x} \\ f\left(\frac{1}{2}\right) &=(-4)^{\frac{1}{2}} \\ f\left(\frac{1}{2}\right) &=\sqrt{-4} \text { not a real number } \end{aligned}\)
实际上,\(f(x)=(−4)^{x}\)任何时候都不是实数\(x\)是带有偶数分母的分数。 所以我们的定义要求\(a>0\)。
通过绘制几个指数函数,我们将能够看到它们的独特属性。
在同一个坐标系图上\(f(x)=2^{x}\)和\(g(x)=3^{x}\).
解决方案:
我们将使用点图来绘制函数图。
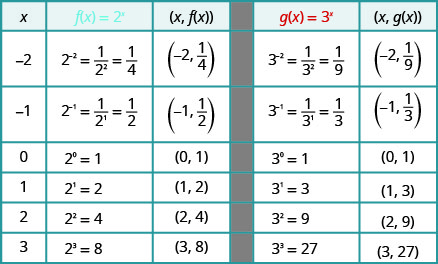
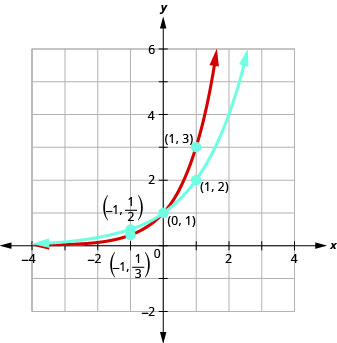
图表:\(f(x)=4^{x}\)。
- 回答
-
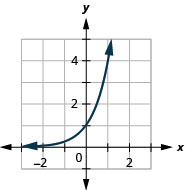
图 10.2.4
图表:\(g(x)=5^{x}\)
- 回答
-
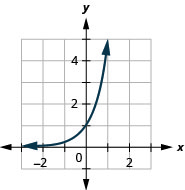
图 10.2.5
如果我们看一下前面示例 10.2.1 和练习 10.2.1 和 10.2.2 中的图表,我们可以识别出指数函数的一些属性。
\(f(x)=2^{x}\)和的图\(g(x)=3^{x}\)以及\(f(x)=4^{x}\)和\(g(x)=5^{x}\)的图形都具有相同的基本形状。 这是我们期望从指数函数得到的形状,其中\(a>1\)。
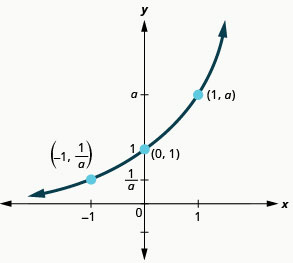
我们注意到,对于每个函数,图中都包含点\((0,1)\)。 这是有道理的,因为\(a^{0}=1\)对任何人来说\(a\).
每个函数的图形\(f(x)=a^{x}\)也包含点\((1,a)\)。 \(f(x)=2^{x}\)包含的图\((1,2)\)和\(g(x)=3^{x}\)包含的图表\((1,3)\)。 这是有道理的,因为\(a^{1}=a\).
还要注意,每个函数的图表\(f(x)=a^{x}\)也包含点\((−1,\frac{1}{a})\)。 \(f(x)=2^{x}\)包含的图\((−1,\frac{1}{2})\)和\(g(x)=3^{x}\)包含的图表\((−1,\frac{1}{3})\)。这很有意义\(a^{−1}=\frac{1}{a}\)。
每个函数的域是什么? 从图中我们可以看出,域是所有实数的集合。 域名没有限制。 我们将区间表示法中的域写为\((−∞,∞)\)。
看看每张图表。 该函数的范围是多少? 图表永远不会碰到\(x\)-axis。 范围均为正数。 我们将间隔表示法中的范围写为\((0,∞)\)。
每当函数的图接近一条直线但从未碰到它时,我们就称该线为渐近线。 对于我们正在研究的指数函数,图形非常接近\(x\)-axis,但永远不会越过它,我们称这条线\(y=0\),即\(x\)-axis,水平渐近线。
\(f(x)=a^{x}\)何时图表的属性\(a>1\)
| 域名 | \((-\infty, \infty)\) |
| 射程 | \((0, \infty)\) |
| \(x\)-截距 | 无 |
| \(y\)-截距 | \((0,1)\) |
| 包含 | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| 渐近线 | \(x\)-axis,直线\(y=0\) |
我们对指数函数的定义是这样\(f(x)=a^{x}\)说的\(a>0\),但是到目前为止的例子和讨论都是关于函数在哪里\(a>1\)。 下一个示例将探讨这种可能性时\(0<a<1\)会发生什么。
在同一个坐标系上,绘制图表\(f(x)=\left(\frac{1}{2}\right)^{x}\)和\(g(x)=\left(\frac{1}{3}\right)^{x}\)。
解决方案:
我们将使用点图来绘制函数图。
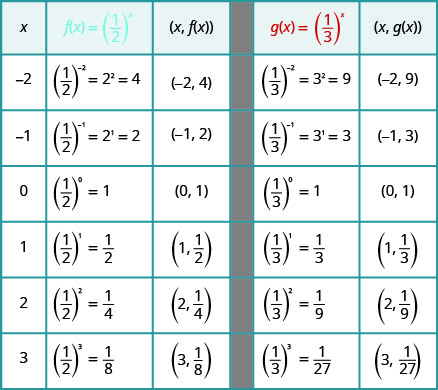
图表:\(f(x)=\left(\frac{1}{4}\right)^{x}\)。
- 回答
-
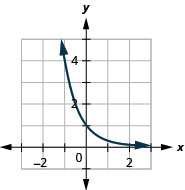
图 10.2.9
图表:\(g(x)=\left(\frac{1}{5}\right)^{x}\)。
- 回答
-
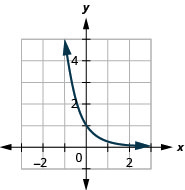
图 10.2.10
现在让我们看一下前面示例 10.2.2 和练习 10.2.3 和 10.2.4 中的图表,这样我们现在就可以确定指数函数的一些属性了\(0<a<1\)。
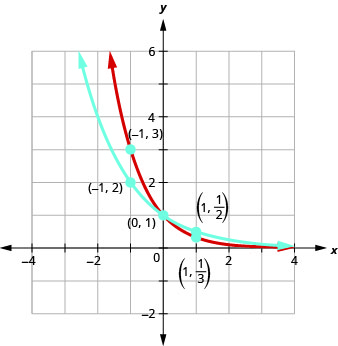
\(f(x)=\left(\frac{1}{2}\right)^{x}\)和的图表\(g(x)=\left(\frac{1}{3}\right)^{x}\)以及\(f(x)=\left(\frac{1}{4}\right)^{x}\)和的图形\(g(x)=\left(\frac{1}{5}\right)^{x}\)都具有相同的基本形状。 虽然这是我们期望从指数函数中得到的形状,其中\(0<a<1\),图形从左向右向下移动,而前面的图形从左向右向上移动。\(a>1\)
我们注意到,对于每个函数,图表仍然包含点\((0, 1)\)。 这是有道理的,因为\(a^{0}=1\)对任何人来说\(a\).
和以前一样,每个函数的图形也包含点\((1,a)\)。\(f(x)=a^{x}\) \(f(x)=\left(\frac{1}{2}\right)^{x}\)包含的图\(\left(1, \frac{1}{2}\right)\)和\(g(x)=\left(\frac{1}{3}\right)^{x}\)包含的图表\(\left(1, \frac{1}{3}\right)\)。 这是有道理的,因为\(a^{1}=a\).
还要注意,每个函数的图形也包含点\(\left(-1, \frac{1}{a}\right)\)。\(f(x)=a^{x}\) \(f(x)=\left(\frac{1}{2}\right)^{x}\)包含的图\((−1,2)\)和\(g(x)=\left(\frac{1}{3}\right)^{x}\)包含的图表\((−1,3)\)。 这是有道理的,因为\(a^{-1}=\frac{1}{a}\).
每个函数的域和范围是多少? 从图中我们可以看出,域是所有实数的集合,我们将区间表示法中的域写成\((−∞,∞)\)。 同样,图表永远不会碰到\(x\)-axis。 范围均为正数。 我们将间隔表示法中的范围写为\((0,∞)\)。
我们将在下表中总结这些属性。 其中还包括何时\(a>1\).
图表的属性\(f(x)=a^{x}\)
| 什么时候\(a>1\) | 什么时候\(0<a<1\) | ||
|---|---|---|---|
| \ (a “>1\)” >域 | \((-\infty, \infty)\) | \ (0<a<1\)” >Domain | \((-\infty, \infty)\) |
| \ (a “>1\)” >范围 | \((0, \infty)\) | \ (0<a<1\)” >Range | \((0, \infty)\) |
| \ (a “>1\)” >\(x\)-intercept | 无 | \ (0<a<1\)” >\(x\)-intercept | 无 |
| \ (a “>1\)” >\(y\)-intercept | \((0,1)\) | \ (0<a<1\)” >\(y\)-intercept | \((0,1)\) |
| \ (a “>1\)” >包含 | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1\) “>包含 | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ (a “>1\)” >渐近线 |
\(x\)-axis,直线\(y=0\) |
\ (0<a<1\)” >渐近线 | \(x\)-axis,直线\(y=0\) |
| \ (a “>1\)” >基本形状 | 增加 | \ (0<a<1\)” >基本形状 | 减少 |
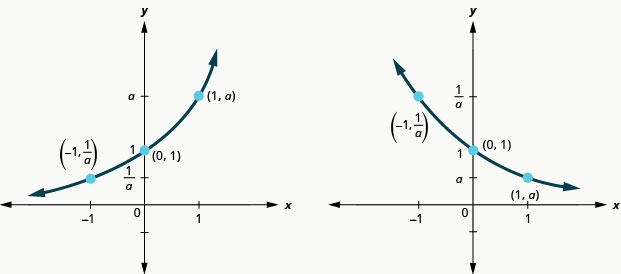
对我们来说,重要的是要注意,这两张图都是一对一的,因为它们都通过了水平线测试。 这意味着指数函数将具有逆函数。 我们稍后再来看这个。
当我们绘制二次函数时,我们能够使用平移来绘制图形,而不仅仅是绘制点。 这在绘制指数函数时行得通吗?
在同一个坐标系图上\(f(x)=2^{x}\)和\(g(x)=2^{x+1}\).
解决方案:
我们将使用点图来绘制函数图。

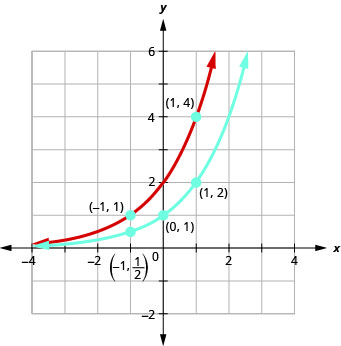
在同一个坐标系上,绘制图表:\(f(x)=2^{x}\)和\(g(x)=2^{x-1}\)。
- 回答
-
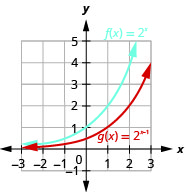
图 10.2.14
在同一个坐标系上,绘制图表\(f(x)=3^{x}\)和\(g(x)=3^{x+1}\)。
- 回答
-
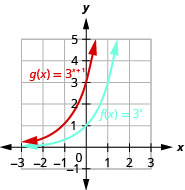
图 10.2.15
看看函数的图表\(f(x)=2^{x}\)和最后一个例子,我们可以看到,\(g(x)=2^{x+1}\)在指数中加一个单位会导致向左水平移动一个单位。 识别这种模式允许我们通过翻译绘制具有相同模式的其他函数。
现在让我们考虑另一种情况,一旦我们识别出这种模式,翻译可能会更容易地绘制出来。
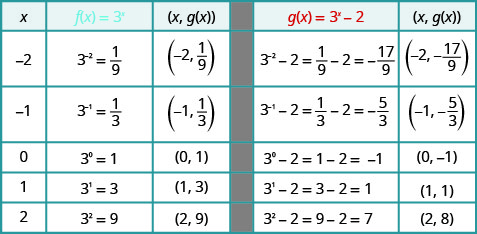
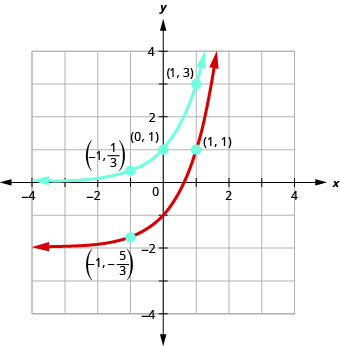
在同一个坐标系图上\(f(x)=3^{x}\)和\(g(x)=3^{x}-2\).
解决方案:
我们将使用点图来绘制函数图。
在同一个坐标系上,绘制图表\(f(x)=3^{x}\)和\(g(x)=3^{x}+2\)。
- 回答
-
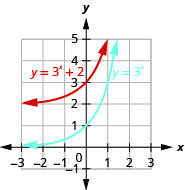
图 10.2.18
在同一个坐标系上,绘制图表\(f(x)=4^{x}\)和\(g(x)=4^{x}-2\)。
- 回答
-
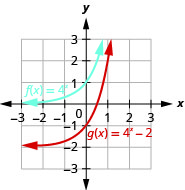
图 10.2.19
看看函数的图表\(f(x)=3^{x}\)和\(g(x)=3^{x}−2\)最后一个例子,我们发现减法\(2\)导致垂直向下移动两个单位。 请注意,水平渐近线也向下移动了\(2\)单位。 识别这种模式允许我们通过翻译绘制具有相同模式的其他函数。
我们所有的指数函数都以整数或有理数作为基数。 我们现在来看一个以非理数为基数的指数函数。
在我们查看这个指数函数之前,我们需要定义非理性数\(e\)。 这个数字被用作许多由指数函数建模的科学和商业应用程序的基础。 该数字被定义为 a\(\left(1+\frac{1}{n}\right)^{n}\) s 的值\(n\)越来越大。 我们说,随着\(n\)接近无穷大,或者无限增加。 该表显示了多个值的值\(n\)。\(\left(1+\frac{1}{n}\right)^{n}\)
| \(n\) | \(\left(1+\frac{1}{n}\right)^{n}\) |
|---|---|
| \ (n\)” >\(1\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2\) |
| \ (n\)” >\(2\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.25\) |
| \ (n\)” >\(5\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.48832\) |
| \ (n\)” >\(10\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.59374246\) |
| \ (n\)” >\(100\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.704813829 \ldots\) |
| \ (n\)” >\(1,000\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.716923932 \ldots\) |
| \ (n\)” >\(10,000\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.718145927 \ldots\) |
| \ (n\)” >\(100,000\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.718268237 \ldots\) |
| \ (n\)” >\(1,000,000\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.718280469 \ldots\) |
| \ (n\)” >\(1,000,000,000\) | \ (\ 左 (1+\ frac {1} {n}\ 右) ^ {n}\)” >\(2.718281827 \ldots\) |
\(e \approx 2.718281827\)
\(e\)这个数字就像数字一样,我们使用符号来表示它,因为它的十进制表示永远不会停止或重复。\(π\) 非理性数\(e\)被称为自然基数。
天然基地\(e\)
该数字\(e\)被定义为的值\(\left(1+\frac{1}{n}\right)^{n}\),无限\(n\)增加。 我们说,随着无限的\(n\)临近,
\(e \approx 2.718281827\)
基数为\(e\)的指数函数\(f(x)=e^{x}\)称为自然指数函数。
自然指数函数
自然指数函数是一个指数函数,其基数为\(e\)
\(f(x)=e^{x}\)
域为\((−∞,∞)\),范围为\((0,∞)\)。
让我们在与\(g(x)=2^{x}\)和相同的坐标系\(f(x)=e^{x}\)上绘制函数图\(h(x)=3^{x}\)。
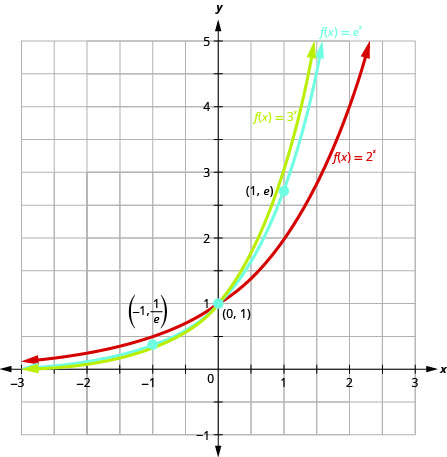
请注意,的图表介\(f(x)=e^{x}\)于 “\(g(x)=2^{x}\)和” 的图表之间\(h(x)=3^{x}\)。这有意义\(2<e<3\)吗?
求解指数方程
包含指数表达式的方程\(a^{x}\)称为指数方程。 为了解决这些问题,我们使用一个属性,表示长为\(a>0\)\(a≠1\) and\(a^{x}=a^{y}\),如果是真的\(x=y\)。 换句话说,在指数方程中,如果基数相等,则指数相等。
指数方程的一对一性质
对于\(a>0\) and\(a≠1\),
如果\(a^{x}=a^{y}\),那么\(x=y\)。
要使用这个属性,我们必须确保方程的两边都用相同的基数书写。
解决:\(3^{2 x-5}=27\)。
解决方案:
| 第 1 步:用相同的基数写下方程的两面。 | 因为左边有底座\(3\),所以我们用底写右边\(3\)。 \(27=3^{3}\) | \(3^{2 x-5}=27\) \(3^{2 x-5}=3^{3}\) |
| 第 2 步:通过将指数设置为相等来写一个新方程。 | 由于基数相同,因此指数必须相等。 | \(2x-5=3\) |
| 步骤 3:求解方程。 |
\(5\)添加到每一面。 除以\(2\)。 |
\(\begin{aligned} 2 x &=8 \\ x &=4 \end{aligned}\) |
| 步骤 4:检查解决方案。 | 替换\(x=4\)成原始方程式。 | \(\begin{aligned} 3^{2 x-5} &=27 \\ 3^{2 \cdot \color{red}{4}\color{black}{-}5} & \stackrel{?}{=} 27 \\ 3^{3} &\stackrel{?}{=}27 \\ 27 &=27 \end{aligned}\) |
解决:\(3^{3 x-2}=81\)。
- 回答
-
\(x=2\)
解决:\(7^{x-3}=7\)。
- 回答
-
\(x=4\)
这些步骤总结如下。
如何求解指数函数
- 如果可能的话,用相同的基数写下方程的两面。
- 通过将指数设置为相等来写一个新方程。
- 求解方程。
- 检查解决方案。
在下一个示例中,我们将使用指数的属性。
解决\(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\)。
解决方案:
| \(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\) | |
| 使用指数的属性:\(\frac{a^{m}}{a^{n}}=a^{m-n}\). | \(e^{x^{2}-3}=e^{2 x}\) |
| 通过将指数设置为相等来写一个新方程。 | \(x^{2}-3=2 x\) |
| 求解方程。 | \(x^{2}-2 x-3=0\) |
| \((x-3)(x+1)=0\) | |
| \(x=3, x=-1\) | |
| 检查解决方案。 | |
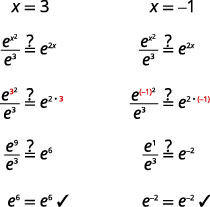 |
解决:\(\frac{e^{x^{2}}}{e^{x}}=e^{2}\)。
- 回答
-
\(x=-1, x=2\)
解决:\(\frac{e^{x^{2}}}{e^{x}}=e^{6}\)。
- 回答
-
\(x=-2, x=3\)
在应用程序中使用指数模型
指数函数可对许多情况进行建模。 如果您拥有银行账户,则说明您已经体验过指数函数的使用。 有两个公式用于确定赚取利息时账户中的余额。 如果本金是按利率投资的\(P\)\(r\),那么\(t\)多年来,新的余额将取决于利息复利的频率。\(A\) 如果每年的利息是复利\(n\)次数,我们使用公式\(A=P\left(1+\frac{r}{n}\right)^{n t}\)。 如果利息持续复利,我们使用公式\(A=Pe^{rt}\)。 这些是复利的公式。
复利
对于按利率投资的本金\(r\),\(t\)多年来,新的余额是:\(P\)\(A\)
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\)
在使用利息公式时,先确定变量的值,然后将其替换为公式通常很有帮助。
总计 $ 投资\(10,000\)于大学基金,用于新孙子. 如果利率为\(5\) %,那么通过每种复利方法,按\(18\)年计算,账户中将有多少?
- 化合物季刊
- 化合物月报
- 持续化合物
解决方案:
确定公式中每个变量的值。 记得将百分比表示为十进制。
\(\begin{aligned} A &=? \\ P &=\$ 10,000 \\ r &=0.05 \\ t &=18 \text { years } \end{aligned}\)
a. 对于季度复利,\(n=4\)。 一年中有\(4\)几个季度。
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
用公式中的值代替。
\(A=10,000\left(1+\frac{0.05}{4}\right)^{4 \cdot 18}\)
计算金额。 在计算器中输入表达式时,请谨慎考虑运算顺序。
\(A=\$ 24,459.20\)
b. 对于月度复利,\(n=12\).一年中有\(12\)几个月。
\(A=P\left(1+\frac{r}{n}\right)^{n t}\)
用公式中的值代替。
\(A=10,000\left(1+\frac{0.05}{12}\right)^{12 \cdot 18}\)
计算金额。
\(A=\$ 24,550.08\)
c. 为了连续复合,
\(A=P e^{r t}\)
用公式中的值代替。
\(A=10,000 e^{0.05 \cdot 18}\)
计算金额。
\(A=\$ 24,596.03\)
安吉拉在储蓄账户\(15,000\)中投资了美元。 如果利率为\(4\) %,那么通过每种复利方法,按\(10\)年计算,账户中将有多少?
- 化合物季刊
- 化合物月报
- 持续化合物
- 回答
-
- $\(22,332.96\)
- $\(22,362.49\)
- $\(22,377.37\)
艾伦投资了美元\(10,000\),投资了一个共同基金。 如果利率为\(5\) %,那么通过每种复利方法,按\(15\)年计算,账户中将有多少?
- 化合物季刊
- 化合物月报
- 持续化合物
- 回答
-
- $\(21,071.81\)
- $\(21,137.04\)
- $\(21,170.00\)
由指数函数建模的其他主题涉及增长和衰退。 两者都使用\(A=Pe^{rt}\)我们用于货币增长的公式。 对于增长和衰退,我们通常使用\(A_{0}\)本金作为原始金额\(P\),而不是称之为本金。 我们看到,指数增长的增长率为正,指数衰减的增长率为负。
指数增长和衰退
对于以一定速度增长或衰减的原始金额\(r\),在一定时间内\(t\),最终量为:\(A_{0}\)\(A\)
\(A=A_{0} e^{r t}\)
指数级增长通常体现在人类、动物或细菌种群的增长中。 我们的下一个例子是病毒的生长。
克里斯是疾病控制与预防中心的研究员,他正在努力了解一种新的危险病毒的行为。 他开始\(100\)对以每小时\(25\)百分比的速度生长的病毒进行实验。 他将在\(24\)几个小时内检查病毒。 他会发现多少病毒?
解决方案:
确定公式中每个变量的值。 务必以十进制形式输入百分比。 确保单位匹配-费率为每小时,时间以小时为单位。
\(\begin{aligned} A &=? \\ A_{0} &=100 \\ r &=0.25 / \text { hour } \\ t &=24 \text { hours } \end{aligned}\)
用公式中的值代替:\(A=A_{0} e^{r t}\)。
\(A=100 e^{0.25 \cdot 24}\)
计算金额。
\(A=40,342.88\)
四舍五入到最接近的完整病毒。
\(A=40,343\)
研究人员会发现\(40,343\)病毒。
疾病控制与预防中心的另一位研究人员丽莎正在研究细菌的生长。 她开始对以每小时\(15\)百分比\(50\)的速度生长的细菌进行实验。 他将每隔一\(8\)小时检查一次细菌。 他会在\(8\)几个小时内发现多少细菌?
- 回答
-
她会发现\(166\)细菌。
生物学家玛丽亚正在观察病毒的生长模式。 她首先讲\(100\)的是以每小时\(10\) %增长的速度增长的病毒。 她会在\(24\)几个小时内检查病毒。 她会发现多少病毒?
- 回答
-
她会发现\(1,102\)病毒。
访问这些在线资源,获取有关评估和绘制指数函数的更多指导和练习。
关键概念
- 图表的属性\(f(x)=a^{x}\):
| 什么时候\(a>1\) | 什么时候\(0<a<1\) | ||
|---|---|---|---|
| \ (a “>1\)” >域 | \((-\infty, \infty)\) | \ (0<a<1\)” >Domain | \((-\infty, \infty)\) |
| \ (a “>1\)” >范围 | \((0, \infty)\) | \ (0<a<1\)” >Range | \((0, \infty)\) |
| \ (a “>1\)” >\(x\)-intercept | 无 | \ (0<a<1\)” >\(x\)-intercept | 无 |
| \ (a “>1\)” >\(y\)-intercept | \((0,1)\) | \ (0<a<1\)” >\(y\)-intercept | \((0,1)\) |
| \ (a “>1\)” >包含 | \((1, a),\left(-1, \frac{1}{a}\right)\) | \ (0<a<1\) “>包含 | \((1, a),\left(-1, \frac{1}{a}\right)\) |
| \ (a “>1\)” >渐近线 |
\(x\)-axis,直线\(y=0\) |
\ (0<a<1\)” >渐近线 | \(x\)-axis,直线\(y=0\) |
| \ (a “>1\)” >基本形状 | 增加 | \ (0<a<1\)” >基本形状 | 减少 |
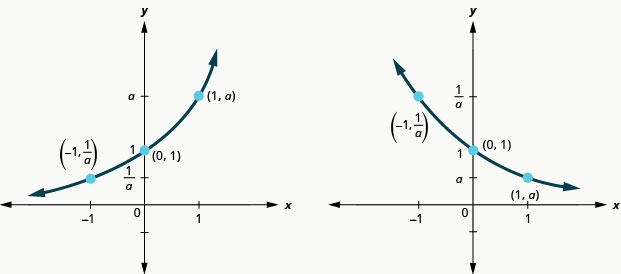
- 指数方程的一对一属性:F
or an\(a>0\) d\(a≠1\),\(A=A_{0} e^{r t}\)
- 如何求解指数方程
- 如果可能的话,用相同的基数写下方程的两面。
- 通过将指数设置为相等来写一个新方程。
- 求解方程。
- 检查解决方案。
- 复利:对于按利率投资的本金\(r\),\(t\)多年来,新余额为\(P\)\(A\)
\(\begin{array}{ll}{A=P\left(1+\frac{r}{n}\right)^{n t}} & {\text { when compounded } n \text { times a year. }} \\ {A=P e^{r t}} & {\text { when compounded continuously. }}\end{array}\) - 指数增长和衰减:对于以一定速率增长或衰减的原始量\(r\),在一定时间\(t\)内\(A\),最终量为\(A=A_{0}e^{rt}\)。\(A_{0}\)
词汇表
- 渐近线
- 函数图近距离接近但从不接触的直线。
- 指数函数
- 指数函数,其中\(a>0\) and 是以下形式的函数\(f(x)=a^{x}\)。\(a≠1\)
- 天然基础
- 数字\(e\)被定义为的值\((1+\frac{1}{n})^{n}\),\(n\)越来越大。 我们说,随着无限\(n\)增长,\(e≈2.718281827...\)
- 自然指数函数
- 自然指数函数是一个指数函数,其基数为\(e\):\(f(x)=e^{x}\)。 域为\((−∞,∞)\),范围为\((0,∞)\)。


