10.3E:练习
- Page ID
- 204040
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
练习成就完美
在以下练习中,绘制每个指数函数的图表。
- \(f(x)=2^{x}\)
- \(g(x)=3^{x}\)
- \(f(x)=6^{x}\)
- \(g(x)=7^{x}\)
- \(f(x)=(1.5)^{x}\)
- \(g(x)=(2.5)^{x}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}\)
- \(g(x)=\left(\frac{1}{3}\right)^{x}\)
- \(f(x)=\left(\frac{1}{6}\right)^{x}\)
- \(g(x)=\left(\frac{1}{7}\right)^{x}\)
- \(f(x)=(0.4)^{x}\)
- \(g(x)=(0.6)^{x}\)
- 回答
-
1。
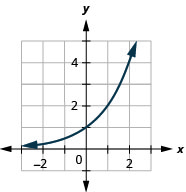
图 10.2.22 3。
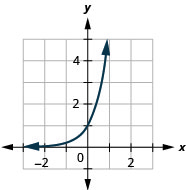
图 10.2.23 5。
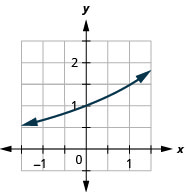
图 10.2.24 7。
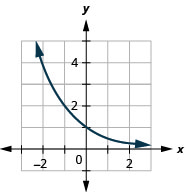
图 10.2.25 9。
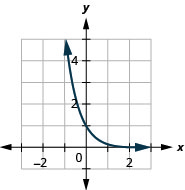
图 10.2.26 11。
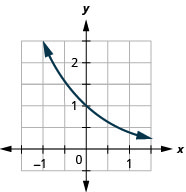
图 10.2.27
在以下练习中,用同一个坐标系绘制每个函数的图表。
- \(f(x)=4^{x}, g(x)=4^{x-1}\)
- \(f(x)=3^{x}, g(x)=3^{x-1}\)
- \(f(x)=2^{x}, g(x)=2^{x-2}\)
- \(f(x)=2^{x}, g(x)=2^{x+2}\)
- \(f(x)=3^{x}, g(x)=3^{x}+2\)
- \(f(x)=4^{x}, g(x)=4^{x}+2\)
- \(f(x)=2^{x}, g(x)=2^{x}+1\)
- \(f(x)=2^{x}, g(x)=2^{x}-1\)
- 回答
-
1。
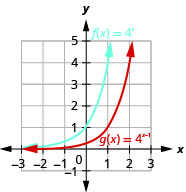
图 10.2.28 3。
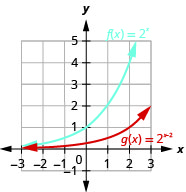
图 10.2.29 5。
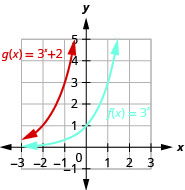
图 10.2.30 7。
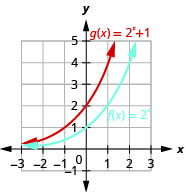
图 10.2.31
在以下练习中,绘制每个指数函数的图表。
- \(f(x)=3^{x+2}\)
- \(f(x)=3^{x-2}\)
- \(f(x)=2^{x}+3\)
- \(f(x)=2^{x}-3\)
- \(f(x)=\left(\frac{1}{2}\right)^{x-4}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}-3\)
- \(f(x)=e^{x}+1\)
- \(f(x)=e^{x-2}\)
- \(f(x)=-2^{x}\)
- \(f(x)=2^{-x-1}-1\)
- 回答
-
1。
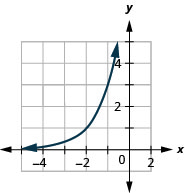
图 10.2.32 3。
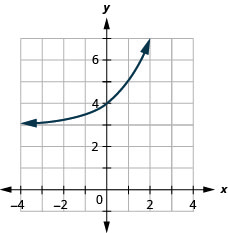
图 10.2.33 5。
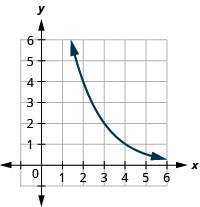
图 10.2.34 7。
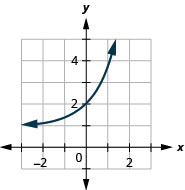
图 10.2.35 9。
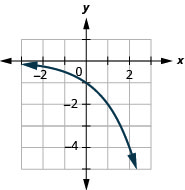
图 10.2.36
在以下练习中,求解每个方程。
- \(2^{3 x-8}=16\)
- \(2^{2 x-3}=32\)
- \(3^{x+3}=9\)
- \(3^{x^{2}}=81\)
- \(4^{x^{2}}=4\)
- \(4^{x}=32\)
- \(4^{x+2}=64\)
- \(4^{x+3}=16\)
- \(2^{x^{2}+2 x}=\frac{1}{2}\)
- \(3^{x^{2}-2 x}=\frac{1}{3}\)
- \(e^{3 x} \cdot e^{4}=e^{10}\)
- \(e^{2 x} \cdot e^{3}=e^{9}\)
- \(\frac{e^{x^{2}}}{e^{2}}=e^{x}\)
- \(\frac{e^{x^{2}}}{e^{3}}=e^{2 x}\)
- 回答
-
1。 \(x=4\)
3。 \(x=-1\)
5。 \(x=-1, x=1\)
7。 \(x=1\)
9。 \(x=-1\)
11。 \(x=2\)
13。 \(x=-1, x=2\)
在以下练习中,将图表与以下函数之一进行匹配:
- \(2^{x}\)
- \(2^{x+1}\)
- \(2^{x-1}\)
- \(2^{x}+2\)
- \(2^{x}-2\)
- \(3^{x}\)
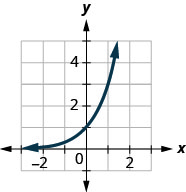
图 10.2.37
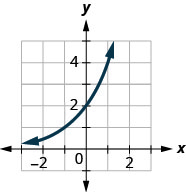
图 10.2.38
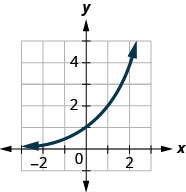
图 10.2.39
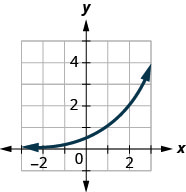
图 10.2.40
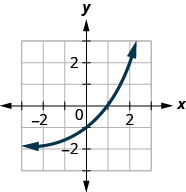
图 10.2.41
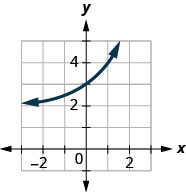
图 10.2.42
- 回答
-
1. f
3. a
5. e
在以下练习中,使用指数模型求解。
- 埃德加累积了 $\(5,000\) 的信用卡债务. 如果利率为每年的\(20\)百分比,并且他\(2\)多年没有偿还任何款项,那么通过每种复利方法,他在\(2\)几年内将欠这笔债务多少钱?
- 化合物季刊
- 化合物月报
- 持续化合物
- 辛西娅在储蓄账户\(12,000\)中投资了美元。 如果利率为\(6\) %,那么通过每种复利方法,按\(10\)年计算,账户中将有多少?
- 化合物季刊
- 化合物月报
- 持续化合物
- 罗谢尔将美元存\(5,000\)入IRA账户。 如果投资的年收益率为\(8\)百分比并且持续复利,那么\(25\)多年来她的投资价值将是多少?
- Nazerhy\(8,000\) 在存款证中存入美元。 年利率为\(6\) %,利息将按季度复利。 该证书在\(10\)几年内价值多少?
- 疾病控制与预防中心的一位研究人员正在研究细菌的生长。 他开始\(100\)对以每小时\(6\)百分比的速度生长的细菌进行实验。 他将每隔一\(8\)小时检查一次细菌。 他会在\(8\)几个小时内发现多少细菌?
- 一位生物学家正在观察病毒的生长模式。 她首先讲\(50\)的是以每小时\(20\) %增长的速度增长的病毒。 她会在\(24\)几个小时内检查病毒。 她会发现多少病毒?
- 在过去的十年中,印度尼西亚的人口以每年的速度增长\(1.12\)% 至\(258,316,051\). 如果这个比率持续下去,那么未来几年的人口会是\(10\)多少?
- 在过去的十年中,巴西的人口以每年的速度增长\(0.9\)% 至\(205,823,665\). 如果这个比率持续下去,那么未来几年的人口会是\(10\)多少?
- 回答
-
1。
- $\(7,387.28\)
- $\(7,434.57\)
- $\(7,459.12\)
3。 $\(36,945.28\)
5。 \(223\)细菌
7。 \(288,929,825\)
- 解释如何区分指数函数和多项式函数。
- 比较和对比\(y=x^{2}\)和的图表\(y=2^{x}\)。
- 随着指数函数的值\(x\)降低,指数函数会发生什么? 图表会穿过\(x\)-轴吗? 解释一下。
- 回答
-
1。 答案会有所不同
3。 答案会有所不同
自检
a. 完成练习后,使用此清单评估您对本节目标的掌握程度。
b. 看完这份清单后,你会怎么做才能对所有目标充满信心?


