10.4:计算对数函数并绘制图表
- Page ID
- 204051
在本节结束时,您将能够:
- 在指数形式和对数形式之间转换
- 评估对数函数
- 绘制对数函数
- 求解对数方程
- 在应用程序中使用对数模型
在开始之前,请参加这个准备测验。
- 解决:\(x^{2}=81\)。
如果您错过了此问题,请查看示例 6.46。 - 评估:\(3^{−2}\)。
如果您错过了此问题,请查看示例 5.15。 - 解决:\(2^{4}=3x−5\)。
如果你错过了这个问题,请查看示例 2.2。
我们花了一些时间来寻找许多函数的逆函数。 用另一个操作 “撤消” 一个操作效果很好。 减去 “撤消” 加法,乘法 “撤消” 除法,取平方根 “撤消” 平方。
当我们研究指数函数时,我们发现它是一对一的,因为它的图通过了水平线测试。 这意味着指数函数确实有逆函数。 如果我们尝试使用代数方法来寻找逆数,就会遇到问题。
\(f(x)=a^{x}\)
用... 重写\(y=f(x)\)。
\(y=a^{x}\)
交换变量\(x\)和\(y\)。
\(x=a^{y}\)
求解\(y\)。
哎呀! 我们没办法解决\(y\)!
为了解决这个问题,我们将以 a 为底的对数函数定义为指数函数的逆函数\(f(x)=a^{x}\)。 我们使用表示法\(f^{−1}(x)=log_{a}x\),说指数函数的逆函数是对数函数。
该函数\(f(x)=\log_{a}x\)是以基数、其中\(a\)\(a>0,x>0\)、和为基数的对数函数\(a≠1\)。
\(y=\log _{a} x\)等同于\(x=a^{y}\)
在指数形式和对数形式之间转换
由于方程\(y=\log _{a} x\)和\(x=a^{y}\)是等效的,我们可以在它们之间来回移动。 这通常是求解一些指数和对数方程的方法。 为了帮助来回转换,让我们仔细看看方程式。 参见图 10.3.1。 注意指数和基数的位置。
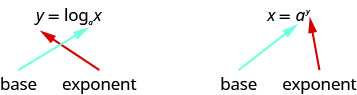
如果我们意识到对数是指数,则转换会更容易。 你可能想重复一遍,“以指数为基数给我们数字。”
转换为对数形式:
- \(2^{3}=8\)
- \(5^{\frac{1}{2}}=\sqrt{5}\)
- \(\left(\frac{1}{2}\right)^{x}=\frac{1}{16}\)
解决方案:
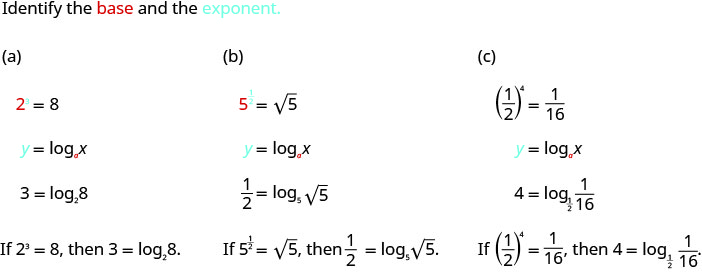
转换为对数形式:
- \(3^{2}=9\)
- \(7^{\frac{1}{2}}=\sqrt{7}\)
- \(\left(\frac{1}{3}\right)^{x}=\frac{1}{27}\)
- 回答
-
- \(\log _{3} 9=2\)
- \(\log _{7} \sqrt{7}=\frac{1}{2}\)
- \(\log _{\frac{1}{3}} \frac{1}{27}=x\)
转换为对数形式:
- \(4^{3}=64\)
- \(4^{\frac{1}{3}}=\sqrt[3]{4}\)
- \(\left(\frac{1}{2}\right)^{x}=\frac{1}{32}\)
- 回答
-
- \(\log _{4} 64=3\)
- \(\log _{4} \sqrt[3]{4}=\frac{1}{3}\)
- \(\log _{\frac{1}{2}} \frac{1}{32}=x\)
在下一个例子中,我们做了相反的——将对数形式转换为指数形式。
转换为指数形式:
- \(2=\log _{8} 64\)
- \(0=\log _{4} 1\)
- \(-3=\log _{10} \frac{1}{1000}\)
解决方案:
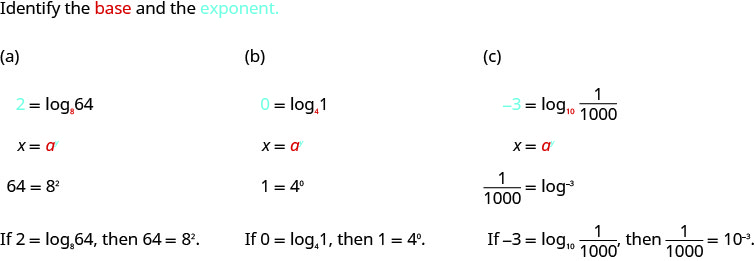
转换为指数形式:
- \(3=\log _{4} 64\)
- \(0=\log _{x} 1\)
- \(-2=\log _{10} \frac{1}{100}\)
- 回答
-
- \(64=4^{3}\)
- \(1=x^{0}\)
- \(\frac{1}{100}=10^{-2}\)
转换为指数形式:
- \(3=\log _{3} 27\)
- \(0=\log _{x} 1\)
- \(-1=\log _{10} \frac{1}{10}\)
- 回答
-
- \(27=3^{3}\)
- \(1=x^{0}\)
- \(\frac{1}{10}=10^{-1}\)
评估对数函数
我们可以使用将方程转换为其等效指数方程的技术来求解和计算对数方程。
找出以下值的值\(x\):
- \(\log _{x} 36=2\)
- \(\log _{4} x=3\)
- \(\log _{\frac{1}{2}} \frac{1}{8}=x\)
解决方案:
一个。
\(\log _{x} 36=2\)
转换为指数形式。
\(x^{2}=36\)
求解二次曲线。
\(x=6, \quad \cancel{x=-6}\)
对数函数的基数必须为正,因此我们消除\(x=−6\)。
\(x=6 \quad\)因此,\(\log _{6} 36=2\)
b。
\(\log _{4} x=3\)
转换为指数形式。
\(4^{3}=x\)
简化。
\(x=64 \quad\)因此\(, \log _{4} 64=3\)
c。
\(\log _{\frac{1}{2}} \frac{1}{8}=x\)
转换为指数形式。
\(\left(\frac{1}{2}\right)^{x}=\frac{1}{8}\)
重写\(\frac{1}{8}\)为\(\left(\frac{1}{2}\right)^{3}\)。
\(\left(\frac{1}{2}\right)^{x}=\left(\frac{1}{2}\right)^{3}\)
在相同的基数下,指数必须相等。
\(x=3 \quad\)因此\(\log _{\frac{1}{2}} \frac{1}{8}=3\)
找出以下值的值\(x\):
- \(\log _{x} 64=2\)
- \(\log _{5} x=3\)
- \(\log _{\frac{1}{2}} \frac{1}{4}=x\)
- 回答
-
- \(x=8\)
- \(x=125\)
- \(x=2\)
找出以下值的值\(x\):
- \(\log _{x} 81=2\)
- \(\log _{3} x=5\)
- \(\log _{\frac{1}{3}} \frac{1}{27}=x\)
- 回答
-
- \(x=9\)
- \(x=243\)
- \(x=3\)
当看到像这样的表达式时\(log_{3}27\),我们可以通过两种方式找到它的确切值。 通过检查,我们意识到这意味着 “\(3\)将拥有什么力量\(27\)”? 从那以后\(3^{3}=27\),我们知道\(log_{3}27=3\)了。 另一种方法是将表达式设置为等于,\(x\)然后将其转换为指数方程。
无需使用计算器即可找到每个对数的确切值:
- \(\log _{5} 25\)
- \(\log _{9} 3\)
- \(\log _{2} \frac{1}{16}\)
解决方案:
一个。
\(\log _{5} 25\)
\(5\)会变成什么力量\(25\)?
\(\log _{5} 25=2\)
或者
将表达式设置为等于\(x\)。
\(\log _{5} 25=x\)
更改为指数形式。
\(5^{x}=25\)
重写\(25\)为\(5^{2}\)。
\(5^{x}=5^{2}\)
在相同的基数下,指数必须相等。
\(x=2 \quad\)因此\(, \log _{5} 25=2\)。
b。
\(\log _{9} 3\)
将表达式设置为等于\(x\)。
\(\log _{9} 3=x\)
更改为指数形式。
\(9^{x}=3\)
重写\(9\)为\(3^{2}\)。
\(\left(3^{2}\right)^{x}=3^{1}\)
简化指数。
\(3^{2 x}=3^{1}\)
在相同的基数下,指数必须相等。
\(2 x=1\)
求解方程。
\(x=\frac{1}{2} \quad\)因此\(, \log _{9} 3=\frac{1}{2}\)。
c。
\(\log _{2} \frac{1}{16}\)
将表达式设置为等于\(x\)。
\(\log _{2} \frac{1}{16}=x\)
更改为指数形式。
\(2^{x}=\frac{1}{16}\)
重写\(16\)为\(2^{4}\)。
\(2^{x}=\frac{1}{2^{4}}\)
\(2^{x}=2^{-4}\)
在相同的基数下,指数必须相等。
\(x=-4 \quad\)因此\(, \log _{2} \frac{1}{16}=-4\)。
无需使用计算器即可找到每个对数的确切值:
- \(\log _{12} 144\)
- \(\log _{4} 2\)
- \(\log _{2} \frac{1}{32}\)
- 回答
-
- \(2\)
- \(\frac{1}{2}\)
- \(-5\)
无需使用计算器即可找到每个对数的确切值:
- \(\log _{9} 81\)
- \(\log _{8} 2\)
- \(\log _{3} \frac{1}{9}\)
- 回答
-
- \(2\)
- \(\frac{1}{3}\)
- \(-2\)
图形对数函数
要绘制对数函数的图形\(y=log_{a}x\),最简单的方法是将方程转换为其指数形式\(x=a^{y}\)。 通常,当我们为函数的图形寻找有序对时,我们通常会选择一个\(x\)-value,然后确定其对应的\(y\)-value。 在这种情况下,你可能会发现选择\(y\)-values 然后确定其对应的-v\(x\) alue 会更容易。
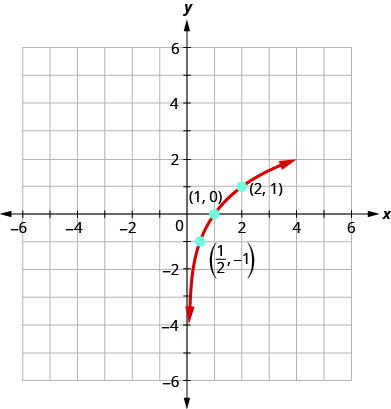
图表\(y=\log _{2} x\)。
解决方案:
要绘制函数的图形,我们将首先以指数形式重写对数方程\(2^{y}=x\)。\(y=\log _{2} x\)
我们将使用点图来绘制函数的图形。 从值开始\(y\)然后获取,会更容易\(x\)。
| \(y\) | \(2^{y}=x\) | \((x,y)\) |
|---|---|---|
| \ (y\)” >\(-2\) | \ (2^ {y} =x\)” >\(2^{-2}=\frac{1}{2^{2}}=\frac{1}{4}\) | \ (x, y)\)” >\((\frac{1}{4},2)\) |
| \ (y\)” >\(-1\) | \ (2^ {y} =x\)” >\(2^{-1}=\frac{1}{2^{1}}=\frac{1}{2}\) | \ (x, y)\)” >\((\frac{1}{2},-1)\) |
| \ (y\)” >\(0\) | \ (2^ {y} =x\)” >\(2^{0}=1\) | \ (x, y)\)” >\((1,0)\) |
| \ (y\)” >\(1\) | \ (2^ {y} =x\)” >\(2^{1}=2\) | \ (x, y)\)” >\((2,1)\) |
| \ (y\)” >\(2\) | \ (2^ {y} =x\)” >\(2^{2}=4\) | \ (x, y)\)” >\((4,2)\) |
| \ (y\)” >\(3\) | \ (2^ {y} =x\)” >\(2^{3}=8\) | \ (x, y)\)” >\((8,3)\) |
图表:\(y=\log _{3} x\)。
- 回答
-
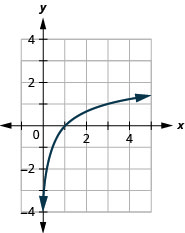
图 10.3.5
图表:\(y=\log _{5} x\)。
- 回答
-
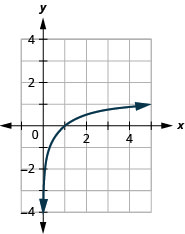
图 10.3.6
和的\(y=\log _{2} x, y=\log _{3} x\)图形\(y=\log _{5} x\)是我们期望从对数函数中获得的形状,其中\(a>1\)。
我们注意到,对于每个函数,图中都包含一个点\((1,0)\)。 这是有道理的,因为\(0=log_{a}1\)\(a^{0}=1\)这意味着对任何人来说都是正确的\(a\)。
每个函数的图形也包含点\((a,1)\)。 这作为\(1=\log _{a} a\)手段是有道理的\(a^{1}=a\)。对任何人来说都是如此\(a\)。
还要注意,每个函数的图表\(y=\log _{a} x\)也包含点\(\left(\frac{1}{a},-1\right)\)。 这作为\(-1=\log _{a} \frac{1}{a}\)手段是有道理的\(a^{-1}=\frac{1}{a}\),对任何人来说都是如此\(a\)。
再看一遍每张图表。 现在我们将看到,对数函数的许多特征只是相应指数函数特征的 “镜像”。
该函数的域是什么? 图表永远不会碰到\(y\)-axis。 该域全部为正数。 我们将区间表示法中的域写为\((0,∞)\)。
每个函数的范围是多少? 从图表中我们可以看出,范围是所有实数的集合。 范围没有限制。 我们将间隔表示法中的范围写为\((−∞,∞)\)。
当图形非常接近\(y\)-axis但永远不会穿过它时,我们称这条直线\(x=0\),即\(y\)-axis,垂直渐近线。
| 域名 | \((0, \infty)\) |
| 射程 | \((-\infty, \infty)\) |
| \(x\)-截距 | \((1,0)\) |
| \(y\)-截距 | 无 |
| 包含 | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| 渐近线 | \(y\)-axis |
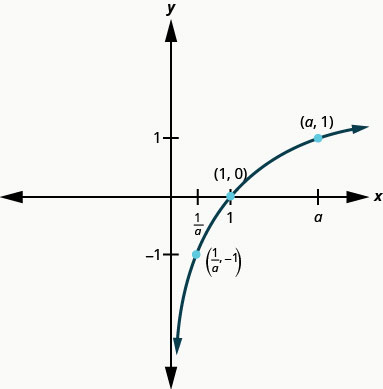
我们的下一个例子是\(y=log_{a}x\)何时的图表\(0<a<1\)。
图表\(y=\log _{\frac{1}{3}} x\)。
解决方案:
要绘制函数的图形,我们将首先以指数形式重写对数方程\(\left(\frac{1}{3}\right)^{y}=x\)。\(y=\log _{\frac{1}{3}} x\)
我们将使用点图来绘制函数的图形。 从值开始\(y\)然后获取,会更容易\(x\)。
| \(y\) | \(\left(\frac{1}{3}\right)^{y}=x\) | \((x,y)\) |
|---|---|---|
| \ (y\)” >\(-2\) | \ (\ left (\ frac {1} {3}\ 右) ^ {y} =x\)” >\(\left(\frac{1}{3}\right)^{-2}=3^{2}=9\) | \ (x, y)\)” >\((9,-2)\) |
| \ (y\)” >\(-1\) | \ (\ left (\ frac {1} {3}\ 右) ^ {y} =x\)” >\(\left(\frac{1}{3}\right)^{-1}=3^{1}=3\) | \ (x, y)\)” >\((3,-1)\) |
| \ (y\)” >\(0\) | \ (\ left (\ frac {1} {3}\ 右) ^ {y} =x\)” >\(\left(\frac{1}{3}\right)^{0}=1\) | \ (x, y)\)” >\((1,0)\) |
| \ (y\)” >\(1\) | \ (\ left (\ frac {1} {3}\ 右) ^ {y} =x\)” >\(\left(\frac{1}{3}\right)^{1}=\frac{1}{3}\) | \ (x, y)\)” >\(\left(\frac{1}{3}, 1\right)\) |
| \ (y\)” >\(2\) | \ (\ left (\ frac {1} {3}\ 右) ^ {y} =x\)” >\(\left(\frac{1}{3}\right)^{2}=\frac{1}{9}\) | \ (x, y)\)” >\(\left(\frac{1}{9}, 2\right)\) |
| \ (y\)” >\(3\) | \ (\ left (\ frac {1} {3}\ 右) ^ {y} =x\)” >\(\left(\frac{1}{3}\right)^{3}=\frac{1}{27}\) | \ (x, y)\)” >\(\left(\frac{1}{27}, 3\right)\) |
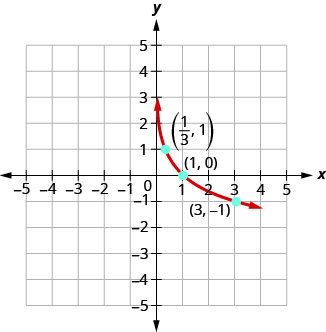
图表:\(y=\log _{\frac{1}{2}} x\)。
- 回答
-
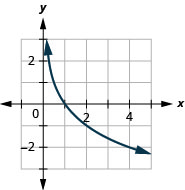
图表:\(y=\log _{\frac{1}{4}} x\)。
- 回答
-
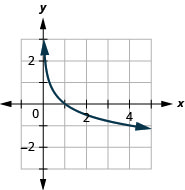
现在,让我们看一下图表\(y=\log _{\frac{1}{2}} x, y=\log _{\frac{1}{3}} x\)和\(y=\log _{\frac{1}{4}} x\),这样我们就可以在哪里找出对数函数的一些属性\(0<a<1\)。
所有图表都具有相同的基本形状。 虽然这是我们期望从对数函数中得到的形状,其中\(0<a<1\)。
我们注意到,同样,对于每个函数,图中都包含点\((1,0),(a, 1),\left(\frac{1}{a},-1\right)\)。 这是有道理的,原因与上面提到的原因相同。
我们注意到域和范围也是一样的——域是\((0,∞)\),范围是\((−∞,∞)\)。 \(y\)-axis 又是垂直渐近线。
我们将在下表中总结这些属性。 其中还包括何时\(a>1\).
| 什么时候\(a>1\) | 什么时候\(0<a<1\) | ||
|---|---|---|---|
| \ (a “>1\)” >域 | \((0, \infty)\) | \ (0<a<1\)” >Domain | \((0, \infty)\) |
| \ (a “>1\)” >范围 | \((-\infty, \infty)\) | \ (0<a<1\)” >Range | \((-\infty, \infty)\) |
| \ (a “>1\)” >\(x\)-intercept | \((1,0)\) | \ (0<a<1\)” >\(x\)-intercept | \((1,0)\) |
| \ (a “>1\)” >\(y\)-intercept | 无 | \ (0<a<1\)” >\(y\)-intercept | 无 |
| \ (a “>1\)” >包含 | \((a, 1),\left(\frac{1}{a},-1\right)\) | \ (0<a<1\) “>包含 | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| \ (a “>1\)” >渐近线 | \(y\)-axis | \ (0<a<1\)” >渐近线 | \(y\)-axis |
| \ (a “>1\)” >基本形状 | 增加 | \ (0<a<1\)” >基本形状 | 减少 |

前面我们讨论过对数函数\(f^{-1}(x)=\log _{a} x\)是指数函数的逆函数\(f(x)=a^{x}\)。 图 10.3.12 中的图表在同一个图形上显示了和的指数(蓝色)和\(a>1\)对数(红色)函数\(0<a<1\)。
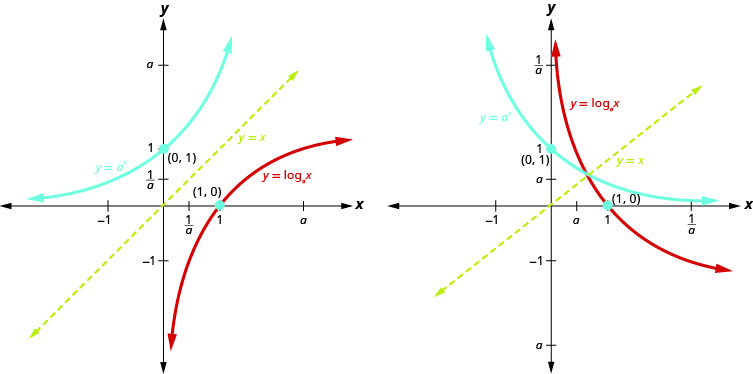
注意图表是如何通过直线相互反射的\(y=x\)。 我们知道逆函数也是如此。 在脑海中保持直观的视觉效果将有助于你记住每个函数的域和范围。 请注意,\(x\)-axis 是指数函数的水平渐近线,而\(y\)-axis 是对数函数的垂直渐近线。
求解对数方程
当我们谈到指数函数时,我们引入了数字\(e\)。 \(e\)就像指数函数的基数一样,它也可以用作对数函数的基数。 带基数的对数函数\(e\)称为自然对数函数。 这个函数通常\(f(x)=\log _{e} x\)是写的\(f(x)=\ln x\),我们把它读作 “el en of”\(x\)。
该函数\(f(x)=\ln x\)是带有底数的自然对数函数\(e\),其中\(x>0\)。
\(y=\ln x\)等同于\(x=e^{y}\)
当对数函数的基数为时\(10\),我们称之为常用对数函数,不显示底数。 如果没有显示对数\(a\)的底数,我们假设它是\(10\)。
该函数\(f(x)=\log x\)是带有底数的常见对数函数\(10\),其中\(x>0\)。
\(y=\log x\)等同于\(x=10^{y}\)

要求解对数方程,一种策略是将方程更改为指数形式,然后像以前一样求解指数方程。 当我们求解对数方程\(y=log_{a}x\)时,我们需要记住这个作为基\(a\)数\(a>0\)和\(a≠1\)。 另外,域是\(x>0\)。 就像激进方程一样,我们必须检查解以消除任何无关的解。
解决:
- \(\log _{a} 49=2\)
- \(\ln x=3\)
解决方案:
一个。
\(\log _{a} 49=2\)
以指数形式重写。
\(a^{2}=49\)
使用平方根属性求解方程。
\(a=\pm 7\)
基数不能为负,所以我们消除\(a=-7\)。
\(a=7, \quad \cancel{a=-7}\)
查看。 \(a=7\)
\(\begin{aligned} \log _{a} 49&=2 \\ \log_{7}49&\stackrel{?}{=}2 \\ 7^{2}&\stackrel{?}{=}49 \\ 49&=49 \end{aligned}\)
b。
\(\ln x=3\)
以指数形式重写。
\(e^{3}=x\)
查看。 \(x=e^{3}\)
\(\begin{aligned} \ln x &=3 \\ \ln e^{3} & \stackrel{?}{=} 3 \\ e^{3} &=e^{3} \end{aligned}\)
解决:
- \(\log _{a} 121=2\)
- \(\ln x=7\)
- 回答
-
- \(a=11\)
- \(x=e^{7}\)
解决:
- \(\log _{a} 64=3\)
- \(\ln x=9\)
- 回答
-
- \(a=4\)
- \(x=e^{9}\)
解决:
- \(\log _{2}(3 x-5)=4\)
- \(\ln e^{2 x}=4\)
解决方案:
一个。
\(\log _{2}(3 x-5)=4\)
以指数形式重写。
\(2^{4}=3 x-5\)
简化。
\(16=3 x-5\)
求解方程。
\(21=3 x\)
\(7=x\)
查看。 \(x=7\)
\(\begin{aligned} \log _{2}(3 x-5)&=4 \\ \log_{2}(3\cdot7-5)&\stackrel{?}{=}4\\ \log_{2}(16)&\stackrel{?}{=}4 \\ 2^{4}& \stackrel{?}{=}16 \\ 16&=16 \end{aligned}\)
b。
\(\ln e^{2 x}=4\)
以指数形式重写。
\(e^{4}=e^{2 x}\)
由于基数相同,因此指数相等。
\(4=2 x\)
求解方程。
\(2=x\)
查看。 \(x=2\)
\(\begin{aligned} \ln e^{2 x} &=4 \\ \ln e^{2 \cdot 2} & \stackrel{?}{=} 4 \\ \ln e^{4} &=4 \\ e^{4} &=e^{4} \end{aligned}\)
解决:
- \(\log _{2}(5 x-1)=6\)
- \(\ln e^{3 x}=6\)
- 回答
-
- \(x=13\)
- \(x=2\)
解决:
- \(\log _{3}(4 x+3)=3\)
- \(\ln e^{4 x}=4\)
- 回答
-
- \(x=6\)
- \(x=1\)
在应用程序中使用对数模型
有许多应用程序是通过对数方程建模的。 我们首先来看给出分贝 (dB) 声音级别的对数方程。 分贝的范围从\(0\)几乎听不见的分贝到可能使耳膜破裂的分贝不\(160\)等。 公式\(10^{−12}\)中的表示几乎听不见的声音强度。
分贝声级
以每平方英寸瓦\(D\)特为单位测量的强度声音的响度等级(以分贝为单位)为\(I\)
\(D=10 \log \left(\frac{I}{10^{-12}}\right)\)
长时间暴露在测量\(85\) dB 的噪音中会对内耳造成永久性损伤,从而导致听力损失。 通过耳机传送的音乐的分贝水平是多少,每平方英寸的强度\(10^{−2}\)瓦特数是多少?
解决方案:
 |
|
| 在强度级别中替换,\(I\)。 | 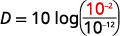 |
| 简化。 | 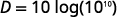 |
| 从那以后\(\log 10^{10}=10\)。 |  |
| 乘以。 | 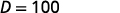 |
| 通过耳机传送的音乐的分贝级别为\(100\) dB。 |
其中一款强度为每平方英寸\(10^{−7}\)瓦特的新型静音洗碗机的分贝水平是多少?
- 回答
-
安静的洗碗机的分贝水平为\(50\) dB。
强度为每平方英寸\(10^{−3}\)瓦特数的密集城市交通量是多少?
- 回答
-
大流量的分贝级别为\(90\) dB。
地震\(R\)的震级由称为里氏标度的对数尺度来测量。 模型是\(R=\log I\),冲击波的强度在哪里\(I\)。 该模型提供了一种测量地震强度的方法。
地震\(R\)的强度由其冲击波的强度来\(R=\log I\)衡量。\(I\)
1906 年,旧金山经历了里氏震级\(7.8\)的强烈地震。 超过\(80\)百分之百的城市被由此产生的大火摧毁。 2014 年,洛杉矶经历了里氏规模的中度地震,造成了数\(108\)百万美元的损失。\(5.1\) 比较两次地震的强度。
解决方案:
要比较强度,我们首先需要使用对数公式将幅度转换为强度。 然后,我们将设置一个比率来比较强度。
将幅度转换为强度。
\(R=\log I\)
1906 年地震
\(7.8=\log I\)
转换为指数形式。
\(I=10^{7.8}\)
2014 年地震
\(5.1=\log I\)
转换为指数形式。
\(I=10^{5.1}\)
形成强度比例。
\(\frac{\text { Intensity for } 1906}{\text { Intensity for } 2014}\)
在值中替换。
\(\frac{10^{7.8}}{10^{5.1}}\)
除以减去指数。
\(10^{2.7}\)
评估。
\(501\)
1906年地震的强度大约是2014年地震强度的两\(501\)倍。
1906 年,旧金山经历了里氏震级\(7.8\)的强烈地震。 1989年,洛马普列塔地震也影响了旧金山地区,并以里氏等级测量\(6.9\)。 比较两次地震的强度。
- 回答
-
1906年地震的强度大约是1989年地震强度的两\(8\)倍。
2014 年,智利经历了里氏震级\(8.2\)的强烈地震。 2014年,洛杉矶还经历了里氏地震。\(5.1\) 比较两次地震的强度。
- 回答
-
智利的地震强度大约是洛杉矶地震强度的两\(1,259\)倍。
访问这些在线资源,获取有关计算和绘制对数函数的更多指导和练习。
关键概念
- 图表的属性\(y=\log _{a} x\):
| 什么时候\(a>1\) | 什么时候\(0<a<1\) | ||
|---|---|---|---|
| \ (a “>1\)” >域 | \((0, \infty)\) | \ (0<a<1\)” >Domain | \((0, \infty)\) |
| \ (a “>1\)” >范围 | \((-\infty, \infty)\) | \ (0<a<1\)” >Range | \((-\infty, \infty)\) |
| \ (a “>1\)” >\(x\)-intercept | \((1,0)\) | \ (0<a<1\)” >\(x\)-intercept | \((1,0)\) |
| \ (a “>1\)” >\(y\)-intercept | 无 | \ (0<a<1\)” >\(y\)-intercept | 无 |
| \ (a “>1\)” >包含 | \((a, 1),\left(\frac{1}{a},-1\right)\) | \ (0<a<1\) “>包含 | \((a, 1),\left(\frac{1}{a},-1\right)\) |
| \ (a “>1\)” >渐近线 | \(y\)-axis | \ (0<a<1\)” >渐近线 | \(y\)-axis |
| \ (a “>1\)” >基本形状 | 增加 | \ (0<a<1\)” >基本形状 | 减少 |

- 分贝声级:强度声音的响度等级\(D\),以分贝为单位\(I\),以瓦特每平方英寸为单位\(D=10 \log \left(\frac{I}{10^{-12}}\right)\)。
- 地震强度:地震\(R\)的震级用其冲击波的强度来\(R=\log I\)衡量。\(I\)
词汇表
- 常见的对数函数
- 该函数\(f(x)=\log x\)是带有底数的常见对数函数\(10\),其中\(x>0\)。
\(y=\log x\)等同于\(x=10^{y}\)
- 对数函数
- 该函数\(f(x)=\log _{a} x\)是以基数、其中\(a\)\(a>0,x>0\)、和为基数的对数函数\(a≠1\)。
\(y=\log _{a} x\)等同于\(x=a^{y}\)
- 自然对数函数
- 该函数\(f(x)=\ln x\)是带有底数的自然对数函数\(e\),其中\(x>0\)。
\(y=\ln x\)等同于\(x=e^{y}\)


