10.4E：练习

第 10.3 节练习

练习成就完美

练习\(\PageIndex{21}\) Convert Between Exponential and Logarithmic Form

在以下练习中，从指数形式转换为对数形式。

1. \(4^{2}=16\)
2. \(2^{5}=32\)
3. \(3^{3}=27\)
4. \(5^{3}=125\)
5. \(10^{3}=1000\)
6. \(10^{-2}=\frac{1}{100}\)
7. \(x^{\frac{1}{2}}=\sqrt{3}\)
8. \(x^{\frac{1}{3}}=\sqrt[3]{6}\)
9. \(32^{x}=\sqrt[4]{32}\)
10. \(17^{x}=\sqrt[5]{17}\)
11. \(\left(\frac{1}{4}\right)^{2}=\frac{1}{16}\)
12. \(\left(\frac{1}{3}\right)^{4}=\frac{1}{81}\)
13. \(3^{-2}=\frac{1}{9}\)
14. \(4^{-3}=\frac{1}{64}\)
15. \(e^{x}=6\)
16. \(e^{3}=x\)

回答

2。 \(\log _{2} 32=5\)

4。 \(\log _{5} 125=3\)

6。 \(\log \frac{1}{100}=-2\)

8。 \(\log _{x} \sqrt[3]{6}=\frac{1}{3}\)

10。 \(\log _{17} \sqrt[5]{17}=x\)

12。 \(\log _{\frac{1}{3}} \frac{1}{81}=4\)

14。 \(\log _{4} \frac{1}{64}=-3\)

16。 \(\ln x=3\)

练习\(\PageIndex{22}\) Convert Between Exponential and Logarithmic Form

在以下练习中，将每个对数方程转换为指数形式。

1. \(3=\log _{4} 64\)
2. \(6=\log _{2} 64\)
3. \(4=\log _{x} 81\)
4. \(5=\log _{x} 32\)
5. \(0=\log _{12} 1\)
6. \(0=\log _{7} 1\)
7. \(1=\log _{3} 3\)
8. \(1=\log _{9} 9\)
9. \(-4=\log _{10} \frac{1}{10,000}\)
10. \(3=\log _{10} 1,000\)
11. \(5=\log _{e} x\)
12. \(x=\log _{e} 43\)

回答

2。 \(64=2^{6}\)

4。 \(32=x^{5}\)

6。 \(1=7^{0}\)

8。 \(9=9^{1}\)

10。 \(1,000=10^{3}\)

12。 \(43=e^{x}\)

练习\(\PageIndex{23}\) Evaluate Logarithmic Functions

在以下练习中，\(x\)在每个对数方程中找到的值。

1. \(\log _{x} 49=2\)
2. \(\log _{x} 121=2\)
3. \(\log _{x} 27=3\)
4. \(\log _{x} 64=3\)
5. \(\log _{3} x=4\)
6. \(\log _{5} x=3\)
7. \(\log _{2} x=-6\)
8. \(\log _{3} x=-5\)
9. \(\log _{\frac{1}{4}} \frac{1}{16}=x\)
10. \(\log _{\frac{1}{3}} \frac{1}{9}=x\)
11. \(\log _{\frac{1}{4}} 64=x\)
12. \(\log _{\frac{1}{9}} 81=x\)

回答

2。 \(x=11\)

4。 \(x=4\)

6。 \(x=125\)

8。 \(x=\frac{1}{243}\)

10。 \(x=2\)

12。 \(x=-2\)

练习\(\PageIndex{24}\) Evaluate Logarithmic Functions

在以下练习中，无需使用计算器即可找到每个对数的确切值。

1. \(\log _{7} 49\)
2. \(\log _{6} 36\)
3. \(\log _{4} 1\)
4. \(\log _{5} 1\)
5. \(\log _{16} 4\)
6. \(\log _{27} 3\)
7. \(\log _{\frac{1}{2}} 2\)
8. \(\log _{\frac{1}{2}} 4\)
9. \(\log _{2} \frac{1}{16}\)
10. \(\log _{3} \frac{1}{27}\)
11. \(\log _{4} \frac{1}{16}\)
12. \(\log _{9} \frac{1}{81}\)

回答

2。 \(2\)

4。 \(0\)

6。 \(\frac{1}{3}\)

8。 \(-2\)

10。 \(-3\)

12。 \(-2\)

练习\(\PageIndex{25}\) Graph Logarithmic Functions

在以下练习中，绘制每个对数函数的图表。

1. \(y=\log _{2} x\)
2. \(y=\log _{4} x\)
3. \(y=\log _{6} x\)
4. \(y=\log _{7} x\)
5. \(y=\log _{1.5} x\)
6. \(y=\log _{2.5} x\)
7. \(y=\log _{\frac{1}{3}} x\)
8. \(y=\log _{\frac{1}{5}} x\)
9. \(y=\log _{0.4} x\)
10. \(y=\log _{0.6} x\)

回答

2。

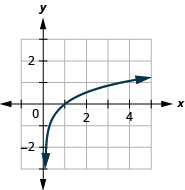
图 10.3.19

4。

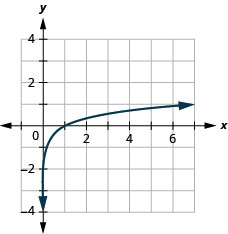
图 10.3.20

6。

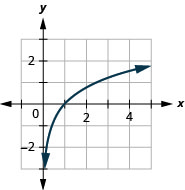
图 10.3.21

8。

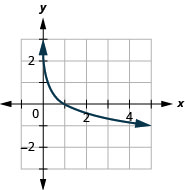
图 10.3.22

10。

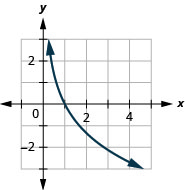
图 10.3.23

练习\(\PageIndex{26}\) Solve Logarithmic Equations

在以下练习中，求解每个对数方程。

1. \(\log _{a} 16=2\)
2. \(\log _{a} 81=2\)
3. \(\log _{a} 8=3\)
4. \(\log _{a} 27=3\)
5. \(\log _{a} 32=2\)
6. \(\log _{a} 24=3\)
7. \(\ln x=5\)
8. \(\ln x=4\)
9. \(\log _{2}(5 x+1)=4\)
10. \(\log _{2}(6 x+2)=5\)
11. \(\log _{3}(4 x-3)=2\)
12. \(\log _{3}(5 x-4)=4\)
13. \(\log _{4}(5 x+6)=3\)
14. \(\log _{4}(3 x-2)=2\)
15. \(\ln e^{4 x}=8\)
16. \(\ln e^{2 x}=6\)
17. \(\log x^{2}=2\)
18. \(\log \left(x^{2}-25\right)=2\)
19. \(\log _{2}\left(x^{2}-4\right)=5\)
20. \(\log _{3}\left(x^{2}+2\right)=3\)

回答

2。 \(a=9\)

4。 \(a=3\)

6。 \(a=\sqrt[3]{24}\)

8。 \(x=e^{4}\)

10。 \(x=5\)

12。 \(x=17\)

14。 \(x=6\)

16。 \(x=3\)

18。 \(x=-5 \sqrt{5}, x=5 \sqrt{5}\)

20。 \(x=-5, x=5\)

练习\(\PageIndex{27}\) Use Logarithmic Models in Applications

在以下练习中，使用对数模型求解。

1. 普通对话的分贝水平是多少，强度为每平方英寸\(10^{−6}\)瓦特？
2. 强度为每平方英寸\(10^{−10}\)瓦特的耳语的分贝等级是多少？
3. 强度为每平方英寸\(10^{−2}\)瓦特数的摩托车噪音的分贝水平是多少？
4. 按每平方英寸\(10^{−2}\)瓦特强度计算，垃圾处理场声音的分贝水平是多少？
5. 2014 年，智利经历了里氏震级\(8.2\)的强烈地震。 2010 年，海地还经历了里氏级\(7.0\)的强烈地震。 比较两次地震的强度。
6. 洛杉矶地区经历了多次地震。 1994年，诺斯里奇地震测得\(6.7\)的震级为里氏等级。 2014年，洛杉矶还经历了里氏地震。\(5.1\) 比较两次地震的强度。

回答

2。 耳语的分贝级别为\(20\) dB。

4。 垃圾处理的声音分贝级别为\(100\) dB。

6。 1994年洛杉矶地区诺斯里奇地震的强度大约是2014年地震强度的两\(40\)倍。

练习\(\PageIndex{28}\) Writing Exercises

1. 解释如何将方程从对数形式更改为指数形式。
2. 解释常用对数和自然对数之间的区别。
3. 解释原因\(\log _{a} a^{x}=x\)。
4. 解释如何在计算器\(\log _{7} 32\)上找到。

回答

2。 答案可能有所不同

4。 答案可能有所不同

自检

a. 完成练习后，使用此清单评估您对本节目标的掌握程度。

图 10.3.24

b. 看完这份清单后，你会怎么做才能对所有目标充满信心？